一种新的电能质量扰动分类方法
2022-05-13
(1.佛山市劲能电力工程有限公司,广东 佛山 528000;2.佛山科学技术学院,广东 佛山 528000)
0 引言
随着国民经济与科学技术的高速发展,用电设备种类繁多,新型电气设备与智能电网投入使用,产生了大量非线性扰动和冲击性扰动。这些非线性扰动和冲击性扰动将影响电网的幅值和频率从而降低电能质量。因此,对电力系统中的扰动信号进行检测与抑制显得尤为重要[1-3]。由于扰动信号大多为非线性,专家学者们采用非线性的信号分析方法如傅里叶变换(FFT)、小波变换、S变换等对电压扰动信号如电压闪变、谐波、脉冲进行检测分类[4-6]。这些方法均取得了较好的成果,但仍有各自的局限性。如傅里叶变化在分析过程中容易出现频谱泄露的问题,文献[7]将短时傅里叶变换与谱峭度相结合,使各谐波分量特征在同一频谱曲线上不再相互干扰。文献[8]采用基于五项最大旁瓣衰减窗六谱线插值FFT的算法,先进行数据拟合进而求出窗函数对应的插值修正公式,可有效的减小计算量。相对于傅里叶变换,小波变换在分析非平稳信号和瞬变信号的能力更强,其检测效果由基函数和分解尺度决定,因此不能确定分解效果是否为最优[9]。文献[10]采用经验小波变换,先将扰动信号进行分解,分解成为具有不同特征时间尺度的单分量成分,以实现各次谐波分量的自动提取。
局部均值分解(LMD)是一种自适应时频分析方法,它能将一个复杂信号逐步分解成为多个乘积函数(PF)之和,而每一个PF分量均为一个包络函数和纯调频函数的乘积,包络函数是PF的瞬时幅值,纯调频函数的频率为PF的瞬时频率。因此,LMD常常用于处理多分量的调幅-调频信号[11]。文献[12]提出一种自适应局部均值法,采用一次样条插值的方法来拟合信号局部均值点,进而得到局部均值曲线。文献[13]采用决策树,对MFDFA的分解特征进行分类,分类效果较好。
本文采用文献[14]中的方法,在信号的左右两端,分别构造一个来自于原始信号的三角波来延拓扰动信号,以抑制局部均值分解的端点效应,并采用神经网络对PF分类进行分类。最后的结果表明,本文的方法可实现对谐波信号的分类,且结构简单,易于硬件实现。
1 局部均值分解
LMD根据电压信号固有的包络特征,将一个复杂的电压信号进行逐级分离,从而得到数个PF分量,每一个PF分量均具有一定物理意义,为包络函数和纯调频函数的乘积[15-16]。对于任意给定信号x(t),分解过程如下:
(1)对于待分解信号所有的局部极值点ni,采用式(1)计算相邻极值点ni,ni+1的平均值mi和幅度包络估计值ai。
(1)
(2)
用折线将相邻的幅度包络估计值与局部均值点连接,平滑处理后将得到包络估计函数a11(t)和局部均值函数m11(t)。
(2)分离局部均值分解函数与原始信号,根据式(2)、式(3)得到新的信号函数h11(t)和调频信号s11(t)。
h11(t)=x(t)-m11(t)
(3)
(4)
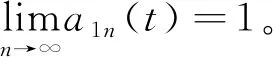
(5)
(6)
为避免迭代次数过多,因此,设定一个变动量Δe,当1-Δe≤a1n(t)≤1+Δe时,终止迭代。
(4)根据式(7)计算幅度包络信号a1(t)。
(7)
(5)根据式(8)计算第一PF分量PF1(t)。
PF1(t)=a1(t)s1n(t)
(8)
(6)在原始信号中分离出PF1(t),将残留信号u1(t)重复分解步骤,循环k次,直到u1(t)为单调函数。
(9)
此时原始信号可重构为:
(10)
2 三角波延拓的设计分析
由于LMD在分解时平滑的长度限制,难以确定信号的终点是否为极限点,因此在信号的两端,设计一个三角波形进行延拓,以左端延拓为例,具体的操作步骤如下[14]:
(1)设定信号x(t)的极大值和极小值分别为mi和ni(i=1,2,3,…),相对应的时间为tmi和tni。信号左端的第一个数据为x(1),对应的第一个极小值与极大值分别为n1和m1,将x(1),m1,n1形成三角基波。
(2)搜索信号中与三角基波最为匹配的三角波形:x(i),mk,nk。起始点x(i)对应的时间点为:
(3)根据式(11)计算所有拓展波形误差e(i)。
e(i)=|mk-m1|+|nk-n1|+|x(i)-x(1)|
(11)
(4)找出式(11)中的最小值emin,设定阈值β。当emin<β,设定emin对应的波形为最佳匹配波形,选择最佳匹配波形前的电压数据作为左端延拓波形。当emin>β,跳转至下一步。
(5)当最小匹配误差超过阈值时,分别选择M个靠近信号端相邻的极大值与极小值,平均处理后作为x(t)的极大值和极小值。将此时的x(t)设为三角基波,跳转至第(2)步。
注意:根据实际情况设定β与M,当原始数据比较规律时,可减小β,反之增大β。
3 神经网络
本文采用三层神经网络,分别为输入层、隐含层、输出层。隐含层通过核函数将输入信号映射到高维空间,输出层在新的空间做线性加权组合[17]。通过不断的迭代,网络的权重将不断更新,最终将误差减少到设定值[18]。本神经网络结构如图1所示。
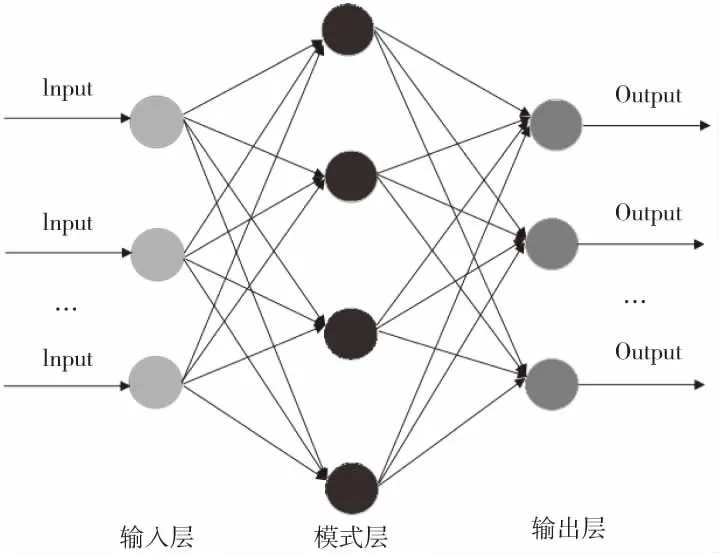
图1 神经网络模型
4 仿真实验及分析
4.1 采用三角波延拓的局部均值分解实验
本文采用电压暂升、电压暂降、暂态振荡、电压中断、脉冲、谐波、闪变等七种电能质量信号进行三角波延拓。七种电能质量信号的扰动模型如表1所示,设置采样频率为2500 HZ,采样长度为0.2 s,每组500点。设置α=0.3,t1=0.02,t2=0.18。采用基于三角波延拓的LMD对其进行信号分解,效果如图2至图8所示。

表1 电能质量扰动模型
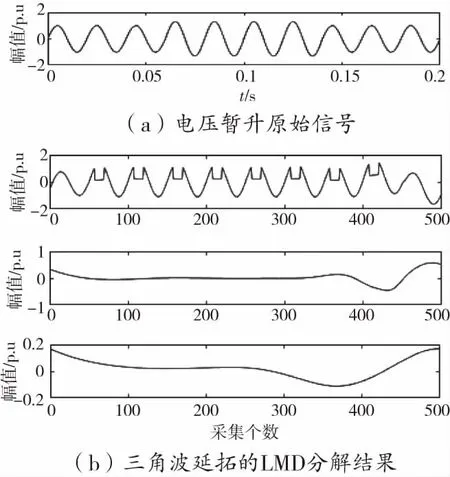
图2 电压暂升信号延拓前后分解对比
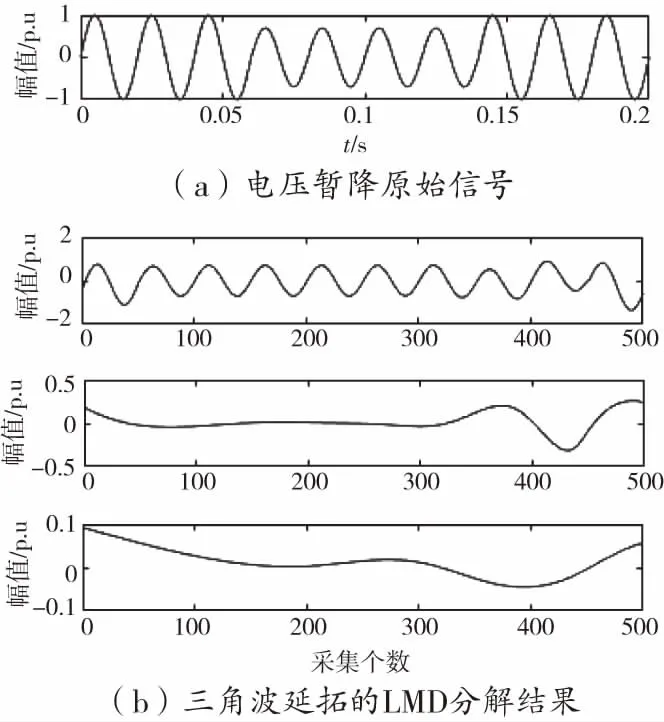
图3 电压暂降信号延拓前后分解对比
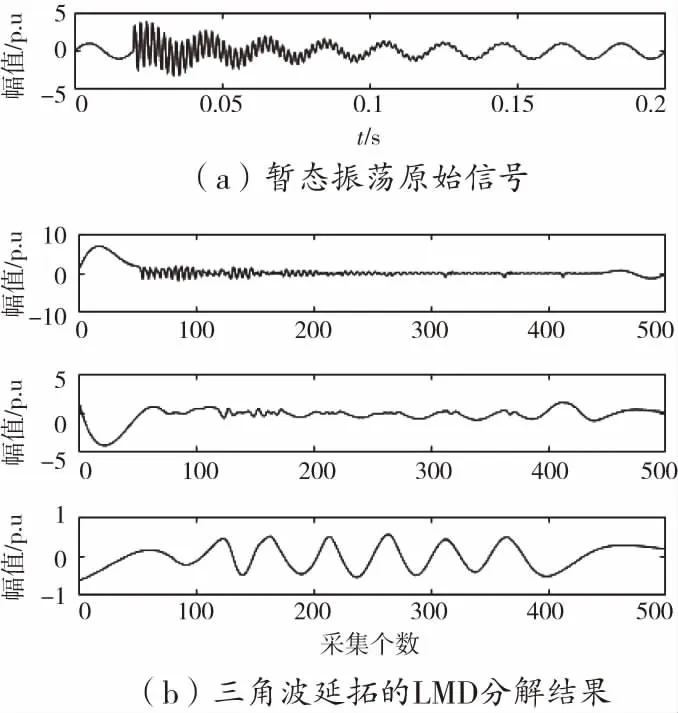
图4 暂态振荡信号延拓前后分解对比
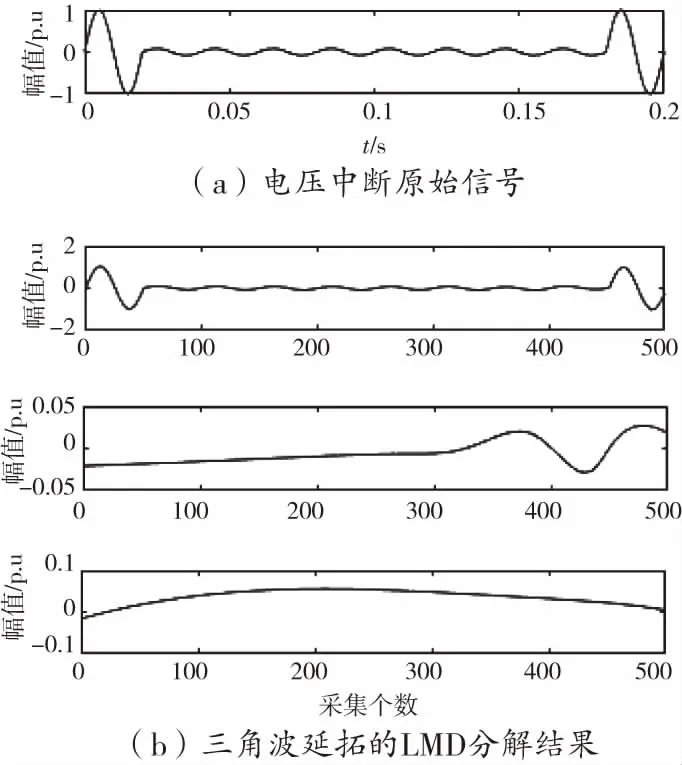
图5 电压中断信号延拓前后分解对比
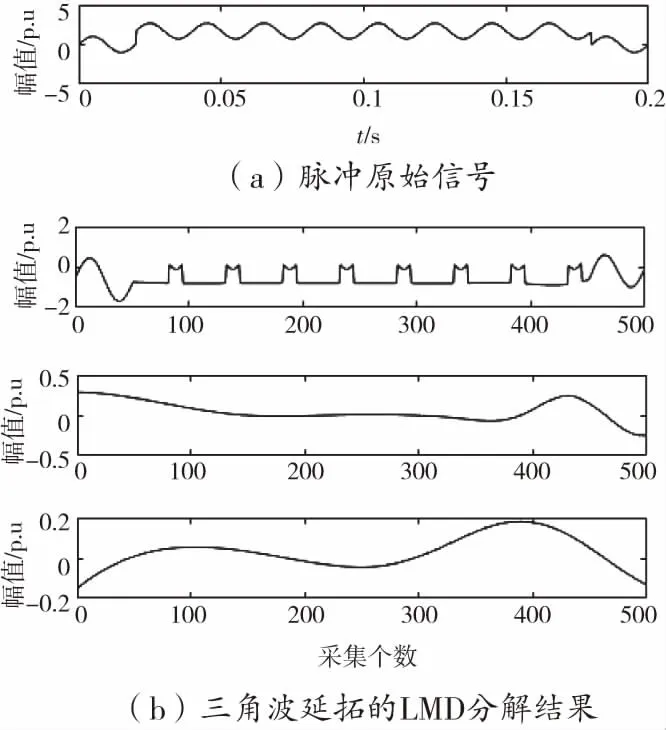
图6 脉冲信号延拓前后分解对比
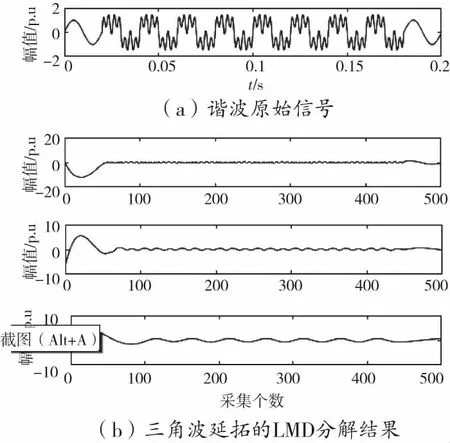
图7 谐波信号延拓前后分解对比
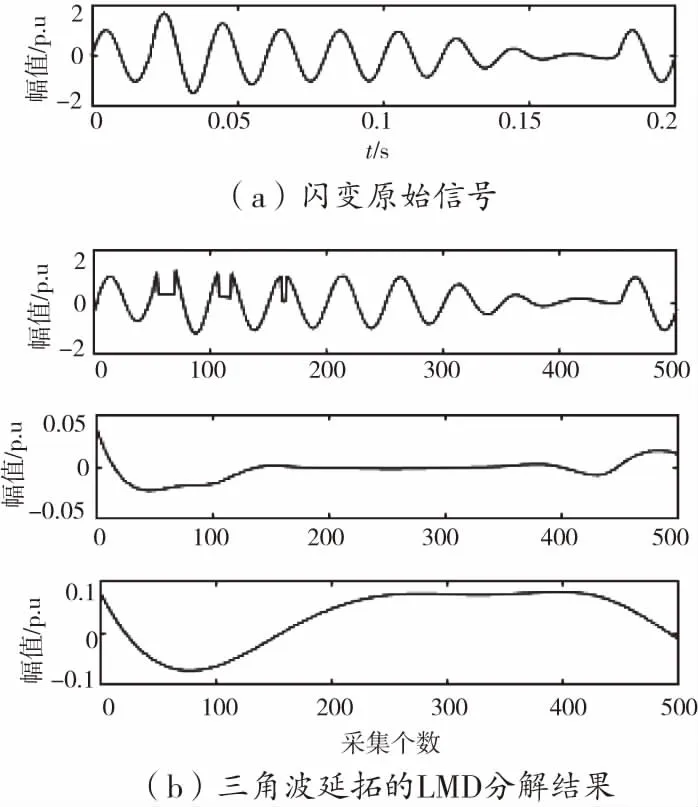
图8 闪变信号延拓前后分解对比
从图2至图8可以看出,三角波延拓之后的分解波形,相对于原始波形变得更平滑。经过三层的逐层分解后,波形即保持了原始的特征,又比原始电压信号平缓。分解后的电压信号,更易于识别,有效的提高分类的精度。
4.2 电压扰动实验
采用MATLAB进行仿真实验,对上面七种电压扰动信号识别分类。首先采用三角波延拓的LMD分解电压信号,分解出三层信号即三种PF分量分别为PF1,PF2,PF3。根基PF分量计算能量值分别为E1,E2,E3。构造能量特征向量T=[E1,E2,E3],将特征向量送去神经网络进行分类,其结果如图9所示。
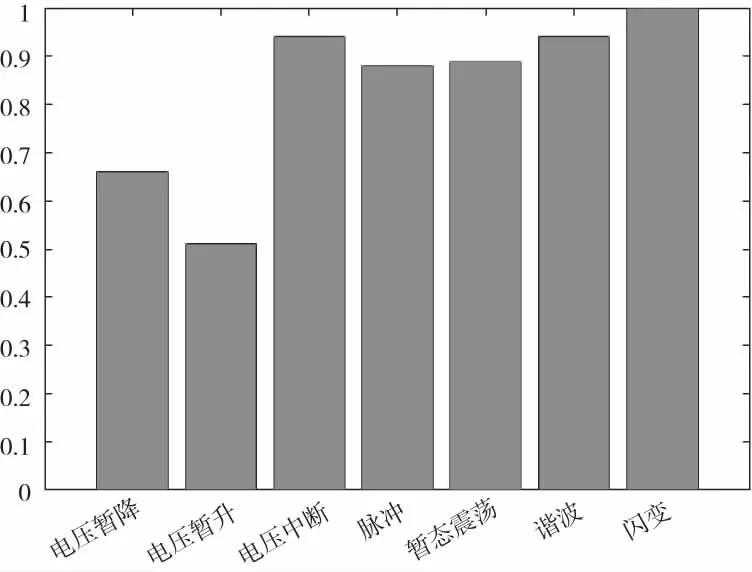
图9 系统仿真结果
从图9中可知,系统可以有效的将七种电压扰动信号分类,其中闪变信号的分类准确率为100%,电压暂降与电压暂升的分类准确率相对较低,其余信号均在90%左右。仿真结果表明,采用三角波延拓的LMD可有效的分解电压信号,由神经网络实现电压信号的分类。
5 结论
本文通过对电压扰动信号建模,采用局部均值分解与神经网络相结合来构建分类模型,实现对电压扰动信号的分类处理。局部均值分解通过三层分解,将七种电压扰动信号转化为电压幅频信息的乘积函数,使用乘积函数构建能量特征矩阵,送入神经网络进行分类。文中的仿真结果表明,该方法可有效的对七种电压扰动信号进行分类。
