基于无人机辅助的认知无线电网络信息年龄研究

曹胜男 贾向东，2 郭艺轩

（1.西北师范大学计算机科学与工程学院，甘肃兰州 730070；2.南京邮电大学江苏省无线通信重点实验室，江苏南京 210003）

1 引言

近年来，随着物联网的快速发展，大量自动化设备需要被提供超可靠低延迟的通信，然而物联网应用设备的迅猛增长使频谱资源变得十分稀缺，无线网络面临着频谱资源短缺的挑战［1］。认知无线电网络（Cognitive Radio Network，CRN）被认为是实现频谱效率更高的通信网络，CRN 利用主通信网络授权的频谱进行能量和信息的传输，提升了现有无线通信网络频谱利用效率［2］。此外，能量受限的物联网设备可能导致数据包的丢失，从而影响信息的及时传递，这对于距离较远或是没有直连链路的物联网设备通信带来了挑战。此时需要设计新的网络体系结构，来有效地利用网络设备有限的能量，达到状态更新的及时交付［3］。由于无人机（Unmanned Aerial Vehicle，UAV）灵活易部署，通常可以保证视距（Line of Sight，LoS）链路，被认为是一个最具潜力的候选无线服务提供商，同时UAV 辅助的无线中继网络也极具发展前景［4］。随着5G/6G 网络对数据时延和新鲜度的极高要求，学术界和工业界广泛认为利用UAV 辅助信息更新系统可以大幅度减小数据的陈旧程度［5］。UAV 网络等新型无线网络应用可以在短时间内进行状态更新和频繁的信息交互。

作为衡量系统性能指标的吞吐量和时延并不能有效地测量信息新鲜度。近年来引入信息年龄（Age of Information，AoI）作为新的性能指标来量化状态更新的新鲜度［6-7］。AoI用于测量数据到达目的节点时的新鲜度，从目的节点的角度观测接收信息的时效性。文献［8］在AoI 的初步研究中考虑流量突发问题，并从排队论的角度最小化了不同服务策略下的AoI。文献［9］和文献［10］分别介绍了先到先服务（First Come and First Served，FCFS）和后到先服务（Last Come and First Served，LCFS）队列的排队理论，并分析了其AoI 特征。文献［11］研究了UAV 辅助无线传感器网络中最优信息年龄的问题，其中UAV从地面传感器节点收集数据。文献［12］研究了以最小化峰值AoI 为目标的零等待策略的最优性。文献［13］研究了在CRN中主用户的AoI和次用户的吞吐量问题。文献［14］研究了CRN能量收集通信中的平均AoI 最小化问题，但没有考虑UAV 通信。文献［15］研究了基于AoI的马尔可夫决策过程来构建状态的更新策略方案。文献［16］研究了低密度奇偶校验编码状态更新系统的平均AoI和能量消耗。

目前大多数研究主要集中在能量采集、复杂的网络结构和传统的性能指标上［17］，而信息的新鲜度和数据传输的及时性对于无线通信也至关重要。此外，频谱资源短缺是一个亟待解决的现实问题，结合UAV 辅助CRN 的AoI 研究相对较少。因此本文考虑了UAV 辅助中继网络来研究CRN 下的峰值AoI。通过联合优化UAV 的飞行轨迹、能量和服务时间分配来最小化峰值AoI。为了求解这一非凸问题，采用了一种有效的迭代算法，并得到了该算法下的近似最优解。

2 系统模型

为了实现及时的信息交付和高效的频谱利用，本文考虑了一种基于UAV 辅助解码转发（Decode and Forward，DF）中继的CRN中AoI最小化问题。如图1 所示，该系统包括一个次用户发射机（Secondary Transmitter，ST）、一个次用户接收机（Secondary Receiver，SR）、一个DF 中继器（DF Relay，R）、一个主用户发射机（Primary Transmitter，PT）和一个主用户接收机（Primary Receive，PR）。系统在半双工模式下运行，除R 外所有节点均配备一个天线。本文假设在Underlay 模式下工作，若PT 所受的干扰小于给定的阈值范围，则次用户（Secondary User，SU）可与主用户（Primary User，PU）进行数据的并发传输，其中PT 始终保持通信工作状态，可在授权频谱中为PR 服务，并在给定的干扰功率约束下与SU 共享频谱资源。假设所有的地面节点的位置是固定已知的，在从系统中，SU 源与目的节点之间的直接链路是弱的，为了数据传输的可靠性，利用UAV 辅助ST向SR 发送数据包，UAV 作为移动中继采用时分双工（Time Division Duplexing，TDD）模式进行上下行链路传输。假设采用实时传输策略，即在SU 目的节点接收到数据包之后，SU 源节点会立即接收到来自对应目的节点的ACK/NACK 信令。此时，SU源节点将再生成一个新的数据包并开始其服务时间。

本文使用AoI 来度量SU 目的节点的信息新鲜度。在t时刻的AoI定义为随机过程：

其中t指当前时间，u(t)为SU 目的节点最近接收到的源节点产生的数据包时间。

如图2 所示，t=0 时刻，队列是空的，此时目的节点的AoI为a(0)=0，Tn为第n个数据包的服务时间，用于上行链路和下行链路的传输时间，N表示UAV 从源节点传输到目的节点的数据包总数。则第n个数据包到达目的节点的时间为tn=。tn时刻的峰值AoI表示为：

由于UAV 中继采用TDD 模式，因此服务时间Tn包括上行传输服务时间Tn，u和下行传输服务时间Tn，d。此外，q(t) ∈R2为UAV 在t，t∈[0，tN]时的飞行轨迹，对于第n个数据包，qn，u表示从ST到UAV 的上行链路传输的路径点，qn，d表示UAV 到SR 的下行链路传输的路径点。将UAV 从初始位置q0到终止位置qF的飞行轨迹进行离散，近似为路径点序列Q={q0，q1，u，q1，d，…，qN，u，qN，d，qF}，同时UAV 满足以下移动性限制：

考虑到在带有一个PU 传输对和一个SU 传输对的网络模型有以下几种情况：（1）PT-PR 的PU 数据传输链路；（2）ST-SR 的SU 数据传输链路；（3）UAV-PR、PT-SR 的干扰链路。假设UAV 与地面节点之间空对地信道为LoS链路通信。本文所有的地面节点（ST、SR、PT 和PR）的位置信息都是先验的，分别为qs，qd，qb，qp。UAV 与地面用户之间的距离表示为，信道功率增益为hrk(t)=ρ0d-2rk(t)，ρ0是参考距离为d=1 m 时的信道功率增益。假设地面信道链路为独立的Rayleigh 衰落，则PT 到SR 的干扰链路的信道功率增益为gbd(t)=ρ0d-φbd(t)ψ，其中φ表示路径损耗指数，ψ是指数分布的单位均值随机变量。

根据香农公式，可以得到上行链路和下行链路的可达率，分别如下式所示：

其中B是传输带宽，σ2是所有接收机的加性高斯白噪声功率，pu(t)和pd(t)分别是ST和UAV的发射功率。

3 AoI分析

本文的目标是最小化CRN 的峰值AoI，通过联合优化UAV 的服务时间Tn、功率分配p={pn，u，pn，d}和飞行轨迹q={qn，u，qn，d}，使CRN 系统N个数据包的峰值AoI 最小，需要满足PU 的平均干扰功率约束、UAV 的移动性约束、各源节点与UAV 的总可用能量约束。将优化问题表述为：

其中Sn为第n个数据包的大小，Eu和Ed分别为ST和UAV 发送更新包的总可用能量。由于P1 是关于p，q和T的非凸性目标函数，因此P1 仍难以解决。为了简化问题，应用Jensen 不等式，得到一个可达的式（4）和式（5）的上界，然后近似代替。

其中pn，u表示ST 在时刻的传输功率，那么同理下行链路的可达率Rn，d可以近似为：

其中pn，d表示UAV 在时刻的传输功率，pn，b为PT的发射功率。

4 联合优化方案

这一节中，提出了一个基于较低复杂度的迭代算法，即连续凸逼近的求解算法来解决问题P1，引入一个松弛变量E来代替式（8）中的p，对于每一个数据包，都有E≜pT，那么问题P1 可以等价的表示为下式：

由于可用能量有限等因素限制，可能造成联合设计方案不可行。因此我们对所提方案进行可行性检查，可行性检查可用于快速决定是否接收或丢弃数据包以最小化峰值AoI。要使问题P2可行，需要同时满足轨迹约束、能量分配约束和服务时间约束条件。

为了使问题更容易解决，引入新变量Tmax来表示目标函数。因此P2可重写为：

解决问题P3主要处理式（14）、式（15）的优化变量E，T，q之间的耦合。故引入一对新的松弛变量来等价的替换非凸约束条件（14）和（15）：

显然，式（20）是一个凸约束条件，式（21）为典型的凸差形式。因此，采用了连续凸逼近的迭代算法来解决这一形式。可以用局部紧但全局下界来近似凸函数。在 点x′n，m∈R++，m∈{u，d}附近的一阶泰勒近似：

将式（23）代入式（21）、（22）中，得到以下不等式：

综上，可以得到凸规划问题P4：

本文基于一个较低计算复杂度的高效迭代的连续凸逼近算法，虽然该算法不是最优的，但是一种更容易解决问题的方式，至少能得到局部最优解。当算法满足条件时停止迭代。

5 仿真及数值结果分析

本节将用数值结果来验证所提问题的可行性和有效性。地面节点的三维坐标分别为PT（0，500，0），PR（1000，500，0），ST（-1000，1000，0），SR（1000，1000，0）。UAV 以飞行高度H=100 m 和最大速度从q0(-1000，0，100) 单向飞行到qF(1000，0，100)。其他参数在表1的描述中给出。

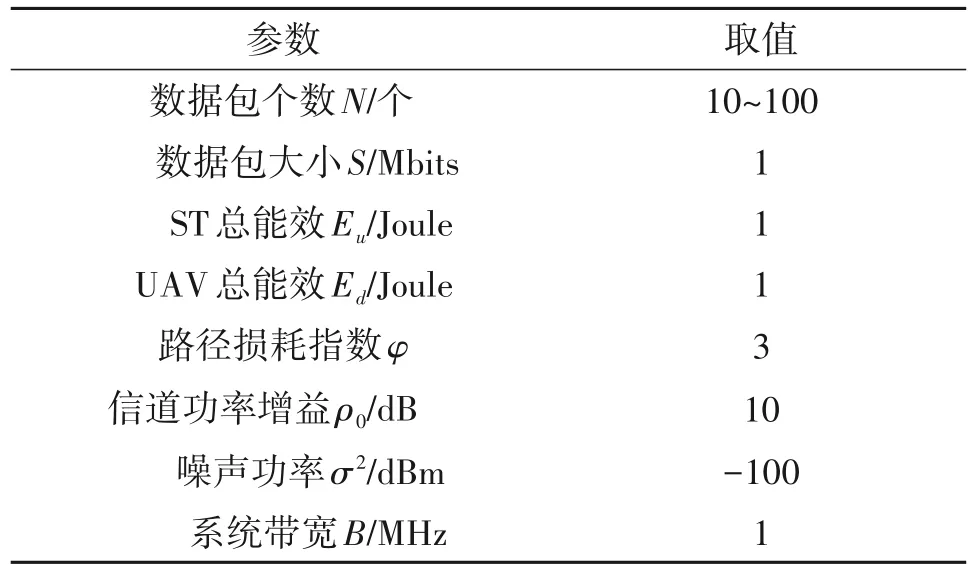
表1 仿真参数Tab.1 Simulation parameters

如图3 所示，描述了N=10 时能量和数据包大小对于峰值AoI 的影响。峰值AoI 随着能量的增大而减小，即能量E越大，峰值AoI 越小。同样，当数据包为1 Mbits 时，比在2 Mbits 的峰值AoI小。在能量E取中间值0.5 J时，两不同的数据包大小之间峰值AoI 时隙为40 s 左右，而在能量E=0.1 J 和E=1.0 J时峰值AoI时隙明显缩小很多。这是因为峰值AoI主要影响因素还有UAV的飞行轨迹。

如图4 所示，是能量E对于UAV 飞行轨迹的影响。当E=1.0 J 时，UAV 飞行倾向于悬停在地面节点上方；当E=1.5 J，UAV就可以相较于地面节点更远的地方传输信息；当E=2.0 J时，UAV就会以最大飞行速度从初始位置直线飞到最终位置，来提升SU之间的高效通信质量并获得较小峰值AoI。

如图5 所示，比较了三种不同服务时间状态下的峰值AoI，分别是在每个服务时间Tn的开始、中间和结束时刻的峰值AoI。开始和中间时刻两曲线很接近，几近重合，虽然服务时间结束时刻的峰值AoI曲线较远，但在能量E=0.4 J 后，三种情况的峰值AoI 曲线近似拟合。故不同的近似方案也会对峰值AoI 结果产生影响，但随着能量的增大，峰值AoI 值基本相等。

如图6 所示，描述了E=1 J，S=1 Mbits、E=1 J，S=2 Mbits 和E=2 J，S=1 Mbits 不同情况下的N=10～100 个数据包特征对峰值AoI 影响。与我们设想一致，数据包S减小和能量E增加，峰值AoI 的值将减小。通过三个方案的对比，当E值相同S不同时，显然S越小，峰值AoI 越小。同理，当S相同E不同时，E越大，峰值AoI 越小。即数据包特征与峰值AoI值成反比。

如图7 所示，比较了数据包N=10 时，所提联合优化方案与UAV直线轨迹的峰值AoI。联合优化方案明显优于直线轨迹，特别是源节点的可用能量较小（7a）或数据包较大（7b）时，相应的峰值AoI 也较大。其中当E=1.0 J 和S=2 Mbits 时，所提优化方案比直线轨迹峰值AoI 分别降低了大约58%和12.5%。同时图（7a）和图（7b）的曲线趋势也验证了图3、图4的仿真结论。

6 结论

本文考虑了一个主用户存在的情况下，次用户通过UAV 辅助中继来收集数据并将数据包传输到相应的次用户终端的问题，提出了一个联合优化方案来优化UAV 的飞行轨迹以及数据传输的能量和服务时间分配。该方案的目标是在满足主接收机平均干扰功率约束的同时，最小化从系统的峰值AoI。由于设计问题是非凸的，通过使用一种较低复杂度的连续凸逼近的迭代算法，在满足可行性条件的同时，得到局部最优解。数值结果证明了该算法的有效性。这项研究工作还可以扩展到传感器网络、随机混合模型中。