堆石料的三维应力分数阶本构模型
2022-05-13吉华孙逸飞
吉华,孙逸飞
(1.中国电建集团 华东勘测设计研究院,杭州 310014;2.河海大学 土木与交通学院,南京 210098;3.德国波鸿鲁尔大学 土木与环境工程学院,波鸿 44801)
堆石料常常被用于水利工程,诸如堆石坝、堤坝等的建造[1]。因此,在此类工程的设计、建造和运营全过程中,堆石料的强度和变形特性显得尤为重要。由于河流水荷载的复杂性,堆石料在其全寿命周期内经常会遭受不同应力路径的外部荷载作用。为了分析不同应力路径下堆石料的强度和变形行为,学者们[2-6]开展了一系列试验和理论研究,并建立了相应的本构模型。Xiao等[5]通过对不同围压和初始密度条件下堆石料的强度和剪胀行为进行研究,提出了状态依赖的堆石料边界面塑性力学本构模型。陈生水等[7]通过研究颗粒破碎对堆石料临界状态特性等的影响,建立了一个可以考虑堆石料颗粒破碎特性的广义塑性力学模型。此外,在实际工程中,堆石料等粗粒土常遭受三维荷载作用,中主应力对其强度和变形行为影响较大[8]。为此,Xiao等[9]提出了基于统一破坏准则的堆石料三维边界面塑性本构模型;姚仰平等[10-11]、Tian等[12]提出了基于转换应力法[13]的软土和粗粒土三维统一硬化模型。为了考虑材料的非关联塑性流动特性,以上这些模型在建立过程中均额外引入了不同于屈服面函数的塑性势面函数。这些塑性势面函数往往基于经验假定。那么,是否可以在不引入塑性势的条件下建立堆石料的三维本构模型呢?为此,Sun等[14]通过分析岩土材料的三轴试验特性,提出了土体的应力分数阶塑性力学方法[14-15]。Lu等[16]基于特征应力法,提出了软土的三维分数阶塑性本构模型。Qu等[17]建立了适用于岩石的分数阶塑性力学模型。李海潮等[18]进一步引入温度效应,拓展建立了软岩的分数阶热塑性模型。这些模型均处于“应力分数阶塑性力学”框架,还有一些诸如“时间分数阶塑性力学”框架下的模型[19],仍然采用屈服面和塑性势面不一致的假定,这里不再赘述。不同于传统塑性力学,应力分数阶塑性力学基于非局域性的分数阶微分算子,在某一应力点求导所得塑性流动方向不仅与该点的应力状态有关,还与到达该点的加载历史或相对临界状态的距离有关。在实际建模过程中,仅需对屈服面进行一阶和分数阶求导,即可建立堆石料的非关联弹塑性本构模型。然而,目前提出的分数阶塑性力学模型[14,20]仅对粗粒土的三轴应力-应变特性进行了分析,对土体真三轴应力-应变特性尚未进行预测和模拟。
为解决这一问题并同时完善现有分数阶岩土塑性力学理论体系,有必要建立一个三维应力分数阶塑性力学本构模型。笔者拟通过特征应力法[21]对现有分数阶塑性力学模型进行修正,使其可以合理地预测土体的三维应力-应变关系。
1 基本定义
1.1 应力-应变的定义


(1)
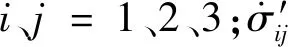
(2)

除此之外,还有平均有效主应力(p′)、偏应力(q)、中主应力系数(b)这几个需要用到的定义。
p′=1/3trσ′
(3)
(4)
(5)
式中:偏应力张量s=σ′-p′I,I为单位张量。
1.2 分数阶导数
Caputo的分数阶左导数和右导数分别定义为[23]
σ′>0+
0->σ′
(6b)

1.3 特征应力法

(7)


(8)
(9)

2 三维分数阶应力-应变关系
增量主应变可以分解为弹性应变和塑性应变两部分,即
(10)

(11)
式中:G是剪切模量;K是体积模量,分别定义为
(12)
(13)


(14)
式中:Kp为硬化模量,其定义将在后面的本构模型部分给出。n和m分别为加载方向和塑性流动方向,定义为[24]
(15)

(16)
式中:df和dg分别定义为
(17)
(18)
在知道屈服面的情况下,分数阶塑性力学模型无需再额外假定一个塑性势面函数,而是通过分数阶微分直接得到一个非关联的流动法则,从而使模型得到简化。由文献[15]可知,当α越大时,所得到的非关联性越明显。具体参见图1,当α由1.05增加到1.3时,同一应力水平下加载方向与流动方向的夹角变大,即非关联程度增加。
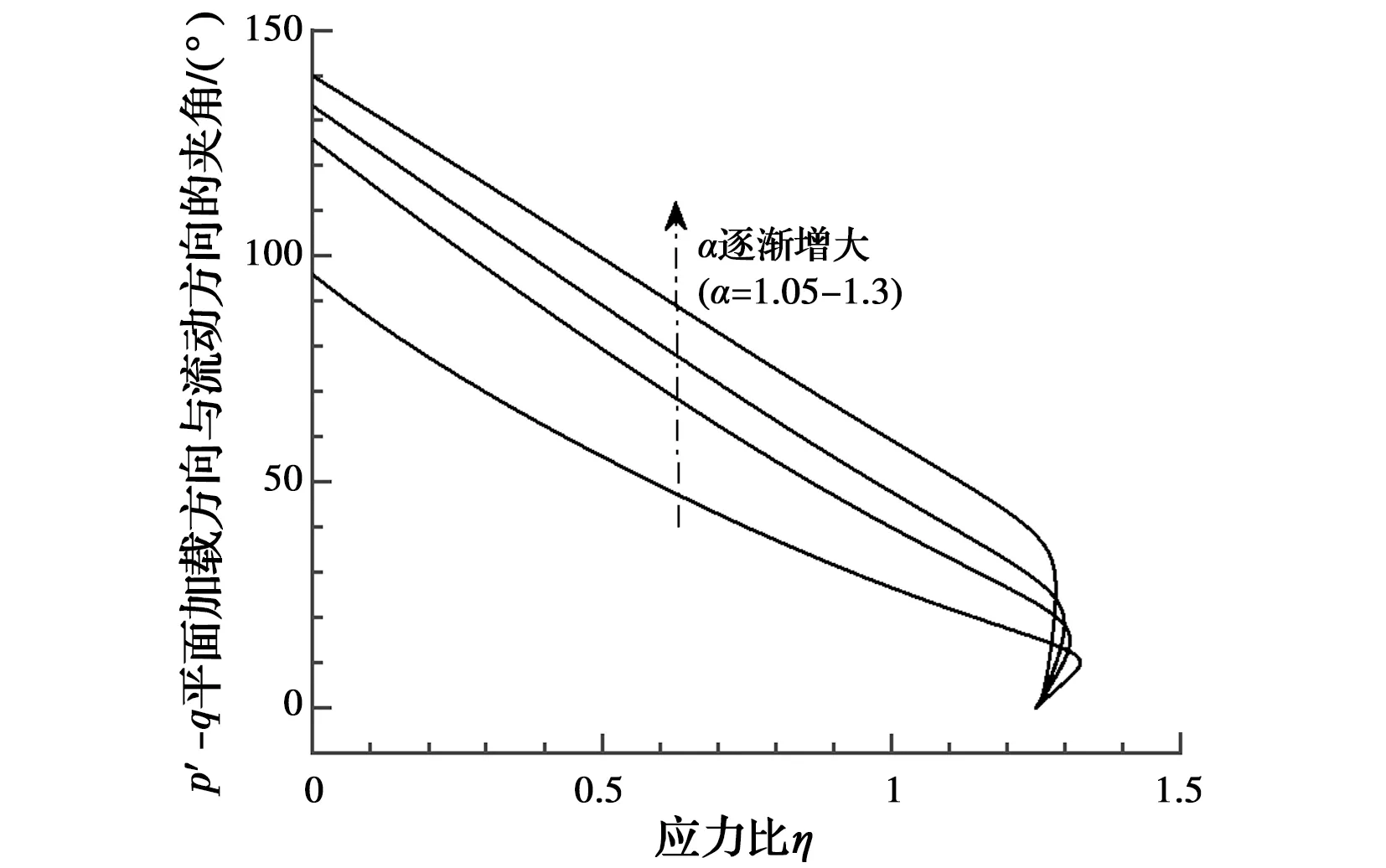
图1 分数阶数对非关联性的影响Fig.1 Effect of fractional order on
3 三维分数阶塑性力学模型
3.1 屈服面
由传统塑性力学可知,加载方向是屈服面的法向。选取特征应力条件下的修正剑桥模型屈服面函数来描述土体的受荷屈服。

(19)

(20)
式中:φc是常规三轴压缩时的临界状态摩擦角。如图2所示,特征应力法修正后的屈服面在常规主应力空间的屈服面不再是一个圆锥,而是一个在π平面的投影,是曲边三角形的曲面,如图3所示。因此,可以反映土体在真三轴应力条件下的屈服特性。

图2 主应力空间的三维屈服面(β=0.4)Fig.2 3D yielding surface in principal stress space

图3 π平面上的屈服面(β=0.2)Fig.3 Yielding surface on the π plane
3.2 加载张量与流动张量
将式(19)分别代入式(17)、式(18),进一步求得df和dg为
(21)
(22)

将式(21)和式(22)代回至式(15)和式(16),即可得到塑性加载张量和塑性流动张量的具体表达式
(23)
(24)
比较式(23)和式(24)可知,当α=1时,模型退化为传统关联流动法则。由图4可知,对屈服面进行分数阶求导后,所得子午平面上塑性流动方向不再垂直于屈服面,而是与加载方向存在一个夹角。

图4 子午平面上的屈服面Fig.4 Yielding surface on the meridian
此外,为了可以反映受荷变形的状态依赖特性,Sun等[14-15]建议采用状态依赖的分数阶数
α=exp(Δψ)
(25)
式中:Δ>0,是材料常数。式(25)是经验公式,来源于基于试验现象的考虑:土体所处状态会影响其塑性流动特性,而分数阶数决定了塑性流动方向。因此,运用式(25)直观地考虑了加载过程中土体所处状态对其塑性流动方向的影响。ψ是状态参数,可以定义为
ψ=e-ec
(26)
式中:ec是临界状态孔隙比,定义为[25]

(27)
式中:eΓ、λ和ξ是e-p′空间的临界状态参数。
3.3 硬化模量
硬化模量描述了土体的硬化特性。Sun等[14]采用Li等[25]提出的常规三轴应力条件下的硬化模量。为了使建立的模型可以反映真三维应力条件下的硬化特性,基于特征应力法修正了Li等[25]的硬化模量,见式(28)。
(28)
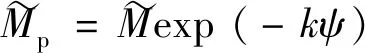
(29)

4 模型参数识别与模型验证
4.1 模型参数识别
模型含有11个参数,分别为:φc、λ、eΓ、ξ、Δ、β、k、h1、h2、G0以及ν。这些模型参数均可以通过三轴试验获得。
参数φc、λ、eΓ和ξ为临界状态参数。φc可以通过拟合p′-q平面临界状态线的斜率得到;λ、eΓ、ξ可以通过拟合e-p′空间的临界状态数据得到[5]。图5所示为临界状态参数对模型预测结果的影响,可见,随着φc和eΓ数值的增加,模型预测得到的同一应变水平下的应力比逐渐增加;随着λ的增加,模型预测的同一应变水平下的应力比逐渐减小。
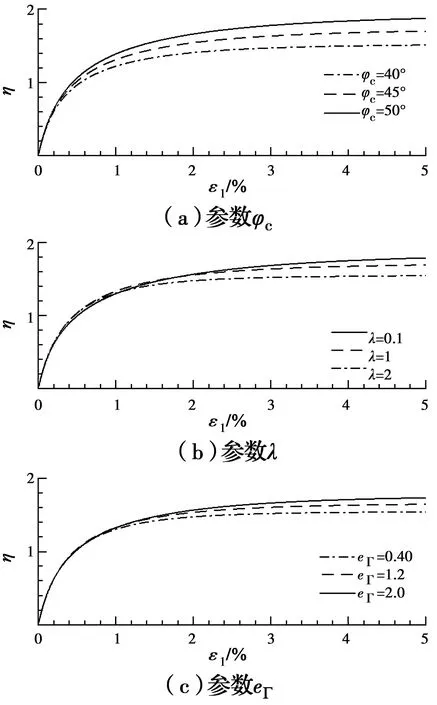
图5 临界状态参数对模型预测的影响Fig.5 Effect of critical-state parameters on model
参数Δ决定了土体的塑性流动特性,可以由试样状态转换时的剪胀关系得到,即d=0。将式(25)代入式(22),得
(30)
因此
(31)

(32)
再将式(29)代入式(32),得
(33)
因此
(34)

参数Δ和k对模型预测的影响见图6。分析发现:随着参数Δ的增加,模型预测得到的同一应变水平下的应力比逐渐增加;随着参数k的增加,模型预测得到的同一应变水平下的应力比逐渐降低。
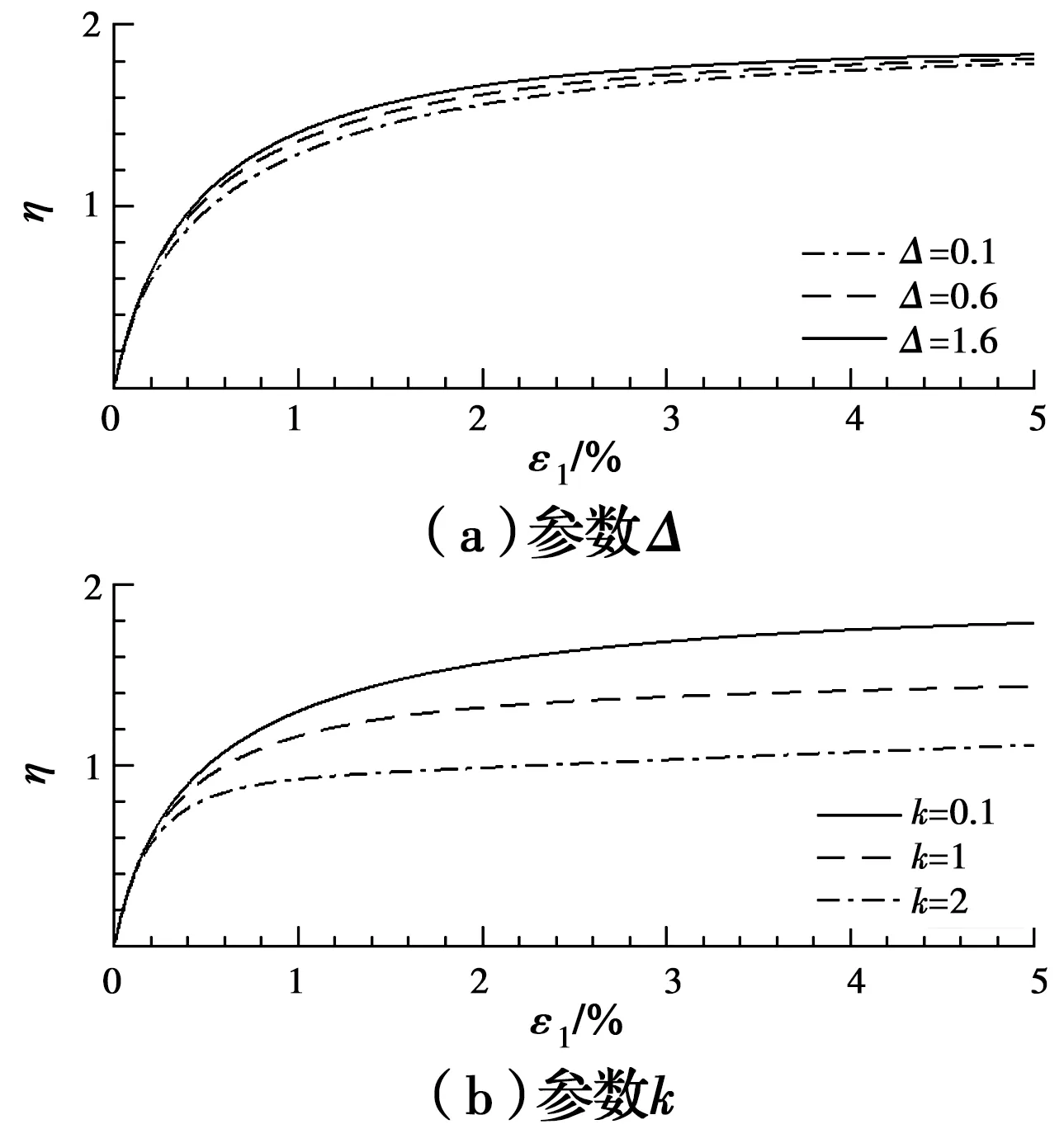
图6 Δ和k对模型预测的影响Fig.6 Effects of Δ and k on model
特征应力参数β可由土体相关三轴压缩(φc)和拉伸(φe)时的临界状态摩擦角关系式获得[21]。β≤0.1时,模型在π平面的屈服轨迹非常接近于Matsuoka-Nakai准则[26]。因此,β近似取0.1。
参数h1和h2可以通过拟合土体受荷时ε1-q关系曲线获得。具体参见文献[15,25],这里不再赘述。图7所示为参数h1和h2对模型预测结果的影响,分析可知:当参数h1增加时,同一应变水平下模型预测的应力比增加;当参数h2增加时,同一应变水平下模型预测的应力比减小。

图7 h1和h2对模型预测的影响Fig.7 Effects of h1 and h2 on model
两个弹性参数(G0、ν)可以通过拟合堆石料初始加载阶段的应力-应变曲线获得,具体参见文献[27]。由于受荷后堆石料弹性变形相对塑性变形较小,因此,不再探讨弹性参数对模型预测的影响。
4.2 模型验证
选取不同初始状态的堆石料[28]在真三轴压缩条件下的试验数据进行拟合和对比,以验证所提出三维分数阶岩土塑性力学模型的合理性。
所选堆石料为两河口心墙土石坝筑坝料,试验初始孔隙比为0.68。试验时固定第三主应力和中主应力比不变,第二和第一主应力按照设定中主应力比值的大小比例增加。其他有关材料和试样准备资料见文献[28],不再赘述。根据前述方法,确定具体模型参数为:G0=90、ν=0.25、φc=46°、λ=0.11、eΓ=0.404、ξ=0.1、Δ=0.2、β=0.1、k=0.1、h1=1.2、h2=0.3。
图8~图10为所提出分数阶塑性力学模型对真三轴试验数据的模拟。对比分析可以发现:模型可以合理地模拟堆石料在不同围压和中主应力比条件下的真三维应力-应变特性。具体来说,随着第一主应变的增加,试样的应力比不断增加;第二主应变只有在中主应力比等于0时,即常规三轴试验条件下,数值为负,其他中主应力比条件下均为正;第三主应变在任何中主应力比条件下均为负值。这些应力-应变特性均可被较好地模拟。

图8 围压100 kPa时三维应力-应变关系的模型预测Fig.8 Model predictions of the 3D stress-strain behavior of rockfill at confining pressure of 100
此外,需要指出的是,中主应力系数较小时,图8~图10中试样在同一偏应力水平所产生的第一主应变大于第二、第三主应变,但随着中主应力系数的增加,第一主应变小于第二、第三主应变;这是因为随着中主应力系数从0变化到1,原先的第二主应力大小慢慢接近于第一主应力,对侧向应变的主导作用逐渐变大。从而在第一主应力方向产生的应变会逐渐小于同等偏应力水平下其他两个主应力方向的应变。

图9 围压150 kPa时三维应力-应变关系的模型预测Fig.9 Model predictions of the 3D stress-strain behavior of rockfill at confining pressure of 150
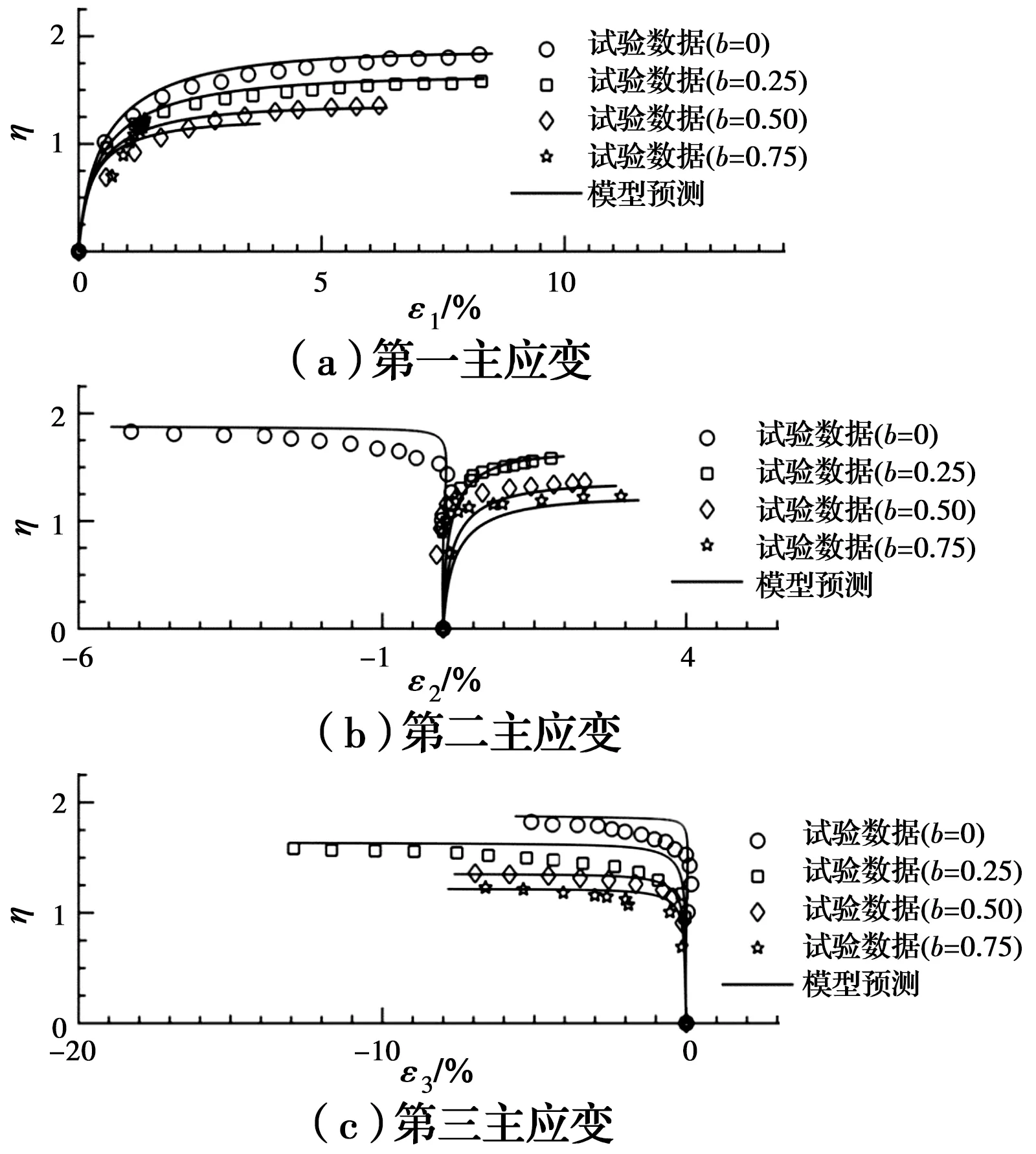
图10 围压200 kPa时三维应力-应变关系的模型预测Fig.10 Model predictions of the 3D stress-strain behavior of rockfill at confining pressure of 200
5 结论
基于特征应力法,修正了已提出的分数阶应力塑性力学模型,使其可以对堆石料在一般三维应力条件下的应力-应变进行预测。并选择堆石料的真三轴压缩试验数据,对模型进了验证。主要结论如下:
1)基于特征应力修正的屈服面,其在主应力空间不再是一个圆锥,而是一个可以反映土体三维屈服特性的曲面,该面在π平面的投影为曲边三角形。
2)无需额外假定塑性势面,只需要对已有屈服面进行分数阶微分求导,便可以得到非关联的流动法则。进一步得出剪胀方程受分数阶求导阶数、特征应力参数以及中主应力系数的影响。
3)基于特征应力法修正了已有常规三轴应力条件下的硬化模量,使其可以反映三维应力条件下堆石料的硬化特性。
4)对比试验数据,验证了所提模型的合理性;模型可以对不同初始状态试样在不同中主应力比条件下的真三轴应力-应变特性进行较好的模拟。
5)建立模型仅考虑了完全饱和堆石料的变形特性,对于干燥或半干燥堆石料遇水饱和后存在的湿化或者软化性能还有待进一步研究。此外,模型也未考虑堆石料在填筑或者运维过程中的颗粒破碎,对于考虑颗粒破碎影响的堆石料三维分数阶塑性模型也有待进一步研究。
