毛竹内嵌杉木的螺栓连接抗拉力学性能

2022-05-13聂诗东罗杨冉松吴迪王辉程睿

土木与环境工程学报 2022年4期

聂诗东，罗杨，冉松，吴迪，王辉，程睿

(重庆大学土木工程学院，重庆 400045)

毛竹是一种纯天然的生物材料，具有生长速度快、成材周期短、力学性能优良等特点。不同毛竹日生长量可达7.5～100 cm[1-2]；在成材周期方面，根据竹子品种和种植情况，通常3～6年就能成材[3]；在力学性能方面，竹子有着不低于木材的力学性能，竹材的强度高、弹性好、性能优良、比重小[4-7]。与钢结构和混凝土结构相比，毛竹结构更轻盈，但对风更敏感。当结构处于风荷载较大区域时，在风吸力作用下，毛竹柱脚会承受反向拉力。而常用毛竹柱脚连接只考虑轴压力，未进行抗拉设计，因此，针对毛竹结构柱脚连接受拉提出新型连接形式并对连接承载能力进行研究。

Ramful[8]提出了一种可以抗拉的毛竹连接，该连接以内嵌于毛竹中空结构内的钢管接头为连接基础，分别设计了喉箍紧固毛竹与内嵌钢管、铆钉连接毛竹与内嵌钢管、自攻螺丝连接毛竹与钢管套筒3种连接形式；Wang等[9]提出了一种利用螺栓连接的抗拉竹连接，并在毛竹里面灌浆以提高连接承载力；Awaludina等[10]提出了一种可以抗拉的连接，该连接以螺杆连接毛竹为基本形式，再用绳子和FRP包裹连接附近毛竹，以提高连接承载力。张楠[11]提出了一种在竹筒内预埋螺栓，再用石膏填充圆竹空腔的抗拉竹节点。林晓雯等[12]提出了一种利用榉木芯和填充剂填充圆竹空腔作为毛竹抗拉节点的方法，并研究了榉木直径、榉木与毛竹内腔间隙量、填充剂、填充剂木纤维添加量对毛竹节点抗拔力的影响。除此之外，还有部分学者也对毛竹抗拉节点进行了研究。现有毛竹抗拉连接节点虽然可以有效用于毛竹受拉时的连接，但仍然存在加工预制尺寸不好确定、湿作业量大、不能有效传递拉力的不足。

笔者提出一种新型内填杉木螺栓连接毛竹抗拉连接，该连接在毛竹内部嵌入杉木，再用螺栓连接杉木和毛竹。内嵌杉木可以限制螺杆弯曲变形，防止螺杆过早弯坏。杉木现场削制，可以适应不同直径的毛竹；两排螺栓连接杉木和毛竹可以有效传递拉力并提供良好的变形能力。针对该新型连接的承载力、变形能力及破坏模式进行研究，提出该连接方式的计算公式，以期得到该连接的设计方法，并用于毛竹结构抗拉连接，推动毛竹结构在实际工程中的应用。

1 试验概况

1.1 试验材料力学性能

试验所用毛竹产自浙江安吉，木材选用杉木，螺栓为4.8级M8、M10、M12、M14、M16五种型号镀锌螺栓，钢板材质为Q235。其中，毛竹由杭州邦博公司进行防腐防霉处理之后，再加工为毛竹连接试件。

毛竹作为一种生物材料，力学性能受诸多因素的影响，如产地、立地条件、朝向、厚度、含水率等均会影响毛竹的力学性能参数。针对不同产地的毛竹力学性能差异较大且力学性能参数离散性大的特点，对试件所用毛竹进行了力学性能试验，包括顺纹抗拉试验、顺纹抗压试验、横纹抗压试验以及含水率试验，得到其顺纹抗拉强度、顺纹抗压强度、横纹抗压强度以及含水率，试验结果如表1所示。

表1 毛竹力学性能试验结果Table 1 Experimental results of mechanical properties of Moso Bamboo

1.2 连接设计

针对毛竹结构内填杉木螺杆连接力学性能进行研究，试件如图1所示。该连接试件由毛竹、内填木材、螺杆、钢板组成。在进行连接加工时，先按照毛竹内径削制所需的杉木，控制杉木直径小于毛竹内径，再用远离端部的螺杆连接毛竹与杉木，最后用靠近端部的螺杆连接毛竹、杉木与钢板，形成整体连接受力。

图1 毛竹结构内填杉木螺栓连接试件Fig.1 Bolt connection specimen of Moso Bamboo structure filled with Chinese

针对不同螺杆直径和螺杆端距下连接的承载力、变形和破坏形式进行研究。针对端距，分别设计了50、80、110 mm 3种端距试件；针对螺杆直径，设计了M8、M10、M12、M14、M16五种直径的试件。具体的试件控制参数及尺寸参数如表2所示。试件编号WS代表试件为内填杉木毛竹连接试件，第1个数字代表螺杆直径，第2个数字代表螺杆端距。

表2 毛竹结构内填杉木连接试件尺寸Table 2 Dimensions of Moso Bamboo connection specimen embedded with Chinese fir

1.3 试验加载方案

采用万能试验机夹持试件钢板对试件进行拉伸试验，如图2所示。采用的试验机最大量程为100 kN，加载时试验机采用位移控制，位移加载速率为2 mm/min，直到试件破坏。利用试验机记录试验过程中试件的荷载-位移曲线，并记录试件的破坏过程和破坏现象。

图2 试验加载图

2 试验结果与分析

2.1 荷载-位移曲线

图3所示为试件的荷载-位移曲线图。结合试件在加载过程中的变形特征和荷载-位移曲线可知，尽管不同试件的变形、破坏形式、极限荷载不同，但试件荷载位移曲线发展过程大体相同。选取典型试件WS-14-80的荷载-位移曲线图进行分析，如图3(d)所示，荷载-位移曲线包括5个阶段：初始滑移阶段、弹性受拉阶段、刚度下降的第2弹性阶段、塑性发展阶段、下降段。

图3 试件荷载-位移曲线Fig.3 Load-displacement curves of

初始滑移阶段ab：由于试件孔洞为预钻孔洞，孔洞的直径略大于螺杆的直径，再加上试件存在初始缺陷，试件的荷载-位移曲线为ab所示的滑移段。连接试件中各组件和加载装置滑移结束后，钢板、螺杆和竹壁三者开始紧密接触，共同受力变形。

弹性受拉阶段bc：此阶段钢板、靠近端部的螺杆、竹壁共同受力变形，拉伸时伴随着毛竹开裂的声音，但毛竹外表面未出现明显裂缝。荷载的增加与变形的增加呈线性关系，螺杆和竹壁均发生弹性变形。当螺杆变形达到一定程度后，毛竹内嵌杉木和第2排螺栓参与连接的受力变形，连接开始进入刚度下降的第2弹性阶段。

刚度下降的第2弹性阶段cd：此阶段毛竹裂缝出现并发展，内嵌杉木和螺栓参与到连接的整体受力，杉木、螺栓、竹壁仍处于弹性阶段，荷载-位移曲线仍呈线性上升。但由于参与协调受力的组成部分增多，荷载-位移曲线表现出刚度下降。

塑性发展阶段de：螺栓、竹壁、杉木变形发展到一定程度进入弹塑性阶段，毛竹裂缝进一步扩大，随着杉木和毛竹纤维的压缩增大，曲线出现非线性塑性段，该段曲线伴随着锯齿状的上升和下降，这是毛竹、杉木开裂等因素所导致。直到连接达到极限荷载，试件开始进入下降段。

下降段ef：连接的变形和裂缝进一步增大，荷载下降，直至螺杆或竹壁发生破坏，加载结束。

2.2 连接承载能力

对于毛竹连接屈服荷载的确定尚未有统一的标准，在确定试件屈服荷载时分别参考了ASTM D5764-97a[13]中建议的5%d偏移法以及Karacabeyli等[14]建议的50%极限荷载法，并将两种方法进行了分析比较。

ASTM D5764-97a中建议的5%d偏移法首先对连接荷载-位移曲线的弹性段进行线性拟合，得到该连接的初始刚度K；随后将拟合到的直线偏移5%d的距离，其与荷载-位移曲线的交点即为屈服荷载Fy，对应的位移为屈服位移Δy；取荷载-位移曲线中峰值点对应的荷载为极限荷载Fu，对应的位移为极限位移Δu，如图4(a)所示。

如图4(b)所示，Karacabeyli等建议的50%极限荷载法则是先取连接荷载位移的峰值点，取峰值的荷载为极限荷载Fu，峰值点的位移为试件的极限位移Δu，屈服点定义为50%Δu对应的点，屈服点的荷载和位移即为试件的屈服荷载Fy和屈服位移Δy。

图4 连接受拉屈服点确定方法Fig.4 Determination method of tensile yield point of

针对提出的新型连接，其荷载-位移曲线存在两个弹性段，采用5%d偏移法进行刚度拟合时存在非唯一性以及主观性，同时，部分试验结果按5%d偏移法进行取值时会出现屈服位移大于极限位移的情况。因此，在确定该类连接的屈服荷载和屈服位移时，不采取ASTM D5764-97a中建议的5%d偏移法。

相较于5%d偏移法，Karacabeyli等建议的50%极限荷载法可以适应毛竹连接承载力离散性大的特点，同时，将50%极限荷载定义为屈服荷载可以使毛竹连接承载力偏于保守，在设计时更加安全。

对连接试件的破坏荷载、破坏位移以及破坏现象进行统计分析，结果如表3所示。可见，按50%极限荷载法确定屈服点时，试件的极限位移均大于屈服位移的2倍，试件从屈服到破坏具有一定的变形能力。

表3 毛竹连接抗拉试验结果Table 3 Tensile test results of Moso Bamboo connection

2.3 连接破坏模式

毛竹内嵌杉木连接的破坏形式主要有螺杆弯断破坏、毛竹壁剪出破坏、毛竹壁开裂破坏3种。

图5(a)为连接螺杆弯断破坏示意图。可见，杉木和竹壁均完整，未发生明显的变形和破坏，螺杆在跨中处发生断裂，螺杆在弯矩作用下变形主要集中在断裂处，螺杆其余部位外形仍较笔直。这种破坏形式发生在螺杆直径小、毛竹壁厚、螺杆端距相对较大的连接。在破坏时竹壁为螺杆提供支撑点，螺杆在跨中钢板的作用下被弯断，连接丧失承载力。

毛竹壁剪出破坏如图5(b)所示，表现为连接的毛竹沿螺杆两边缘产生两条裂缝，毛竹块整体被剪出。这种破坏发生在螺杆直径较大且端距较小的连接。在受力时竹壁承压，当压力过大时毛竹块被整体剪出，连接丧失承载力。

毛竹壁开裂破坏如图5(c)所示，连接在4根螺杆组成的平面发生毛竹竹壁撕裂破坏，产生从外排螺杆贯穿到试件边缘的裂缝。这种连接破坏发生在螺杆直径适中或较大且端距较大的连接。由于孔壁承压力不足以大到将毛竹块整体剪出，且螺杆弯矩不足以将螺杆弯坏，因此，在毛竹壁产生撕裂，导致连接丧失承载力。

由于连接内嵌有杉木，限制了毛竹壁在螺杆作用下的孔壁承压变形，因此，所有连接均未发生明显的孔壁承压变形，这也是该新型连接的一大优势。

图5 毛竹连接试件典型破坏现象Fig.5 Typical failure phenomenons of Moso Bamboo

2.4 屈服荷载影响因素

当螺杆直径小，竹壁还未完全发挥承压能力时，螺杆就已经先发生弯曲破坏；当螺杆直径大到螺杆和竹壁承载力相当，毛竹和螺杆协同受力和变形，试件达到极限荷载时，螺杆和竹壁几乎同时丧失承载力；当螺杆直径大到承载力远高于竹壁承载力，竹壁已经发生破坏时，螺杆承载力还有较大富余，此时试件发生破坏时变形较小。

如图6(b)、(c)所示，对于端距为80、110 mm的试件而言，连接的承载力随着螺杆直径的增大而增大，对于同一端距的试件，当螺杆直径从8 mm增大到16 mm时，连接的承载力可提高两倍以上。而对于端距为50 mm的试件，如图6(a)所示，除试件WS-12-50外，其余试件屈服荷载也随着螺杆直径的增大而增大。将所有试件屈服荷载与螺杆直径关系用散点图表示，并采用直线拟合，如图6(d)所示。少数拟合结果与试验值偏差较大，这是因为毛竹本身具有较大的离散性，但拟合直线明显具有上升趋势。可见，当螺杆直径增大时，连接的屈服荷载也会增大。

图6 螺栓直径与试件屈服荷载的关系Fig.6 Relationship between bolt diameter and yield

将WS-12-50与WS-14-50、WS-16-50的破坏情况进行比较，如图7所示。3个试件均为竹壁剪出破坏，但WS-12-50的螺杆存在明显的挤压竹壁现象，螺帽一侧内陷后将竹壁与杉木挤压在一起，形成锁扣效应，导致其连接承载力高于WS-14-50、WS-16-50。

图7 试件破坏现象

图8为螺杆端距与试件屈服荷载之间的关系图。对于同一直径的螺杆，随着端距的变化，试件的屈服荷载也在发生变化，但不同螺杆直径的屈服荷载变化趋势不同。具体地，M8、M14和M16螺杆的试件，端距为80 mm时屈服荷载最大，端距为110 mm时次之，端距为50 mm时屈服荷载最小；采用M10和M12螺杆的试件，屈服荷载随着试件端距的增大而减小。可见试件的屈服荷载与螺杆端距绝对值没有明显的关系，但在端距为80 mm时试件具有较高的承载力。

图8 螺杆端距与试件屈服荷载的关系Fig.8 Relationship between yield load and end

综上所述，试件的屈服荷载随着螺杆直径的增大而增大，屈服荷载与螺杆端距没有明显关系，但在80 mm时试件具有较高承载力，建议螺杆端距不小于80 mm。

2.5 破坏模式的影响因素

统计不同螺杆直径试件的破坏现象，如表4所示。由表4可见，对于螺杆弯坏，试件的螺杆直径很小，螺杆弯坏发生在螺杆直径为8～10 mm的试件，弯坏试件螺杆直径平均值为8.5 mm，因为螺杆直径小，在竹壁还未屈服时，螺杆就已经弯坏；对于竹壁剪出，螺杆的直径很大，竹壁剪出发生在螺杆直径为14～16 mm的试件，竹壁剪出的螺杆直径平均值为14.8 mm，因为螺杆直径大，承载力高，在较大荷载下，螺杆还未发生较大变形时，竹壁已经被剪出；对于竹壁开裂，试件的螺杆直径为10、12、16 mm时，竹壁开裂螺杆直径的平均值为12.7 mm，这种情况下，螺杆和竹壁的承载力接近，不容易造成螺杆提前弯坏以及竹壁提前剪出的情况。建议选取的螺杆直径不小于10 mm，可以优先选取M12和M10的螺杆。统计不同破坏模式下的端距相对值，如表5所示。可见螺杆弯坏的试件端距在5.0d～13.7d之间，平均值为8.7d；螺杆剪出的试件端距在3.1d～7.8d之间，平均值为5.0d；竹壁开裂的试件端距在5.0～11.0d之间，平均值为7.8d。可以得出结论：当连接端距在5.0d以下时，只会发生竹壁剪出破坏；连接端距在5.0d～7.8d之间时，3种破坏都可能发生；连接端距在7.8d～11.0d之间时，可能发生竹壁开裂和螺杆弯坏；连接端距在11.0d以上时，只会发生螺杆弯坏。

表4 不同螺杆直径试件破坏模式统计表Table 4 Statistical table of failure modes of specimens with different screw diameters

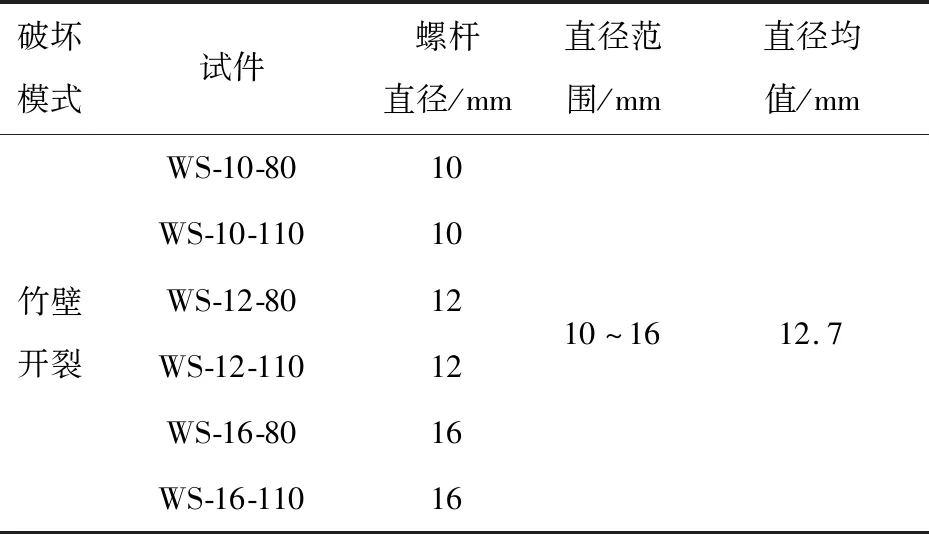
续表4

表5 不同破坏模式螺杆端距统计表Table 5 Statistical table of screw end distance under different failure modes

将本试验内填杉木的毛竹连接与胡行等[15]未填木材的毛竹连接进行对比，选取的比较对象为参数接近的试件，两者的试验参数以及试验条件如表6所示。在试验条件相对一致和试件尺寸差别不大的情况下，内填杉木连接的极限承载力最大值为未填木材连接的1.77倍，可见毛竹内填杉木后对连接的承载力有较大提升。在破坏模式方面，内填杉木的连接没有孔壁滑移破坏模式；在螺杆变形方面，内填杉木连接的螺栓变形也相对较小。

3 承载力计算公式

在进行承载力公式推导时，针对螺杆弯断情况，通过受力分析推导了连接承载力计算式；针对竹壁剪出和竹壁开裂情况，参考Eurocode[16]计算公式形式并引入计算系数，经拟合得到连接承载力计算公式。最后综合二者，提出内嵌杉木连接的承载力设计方法。

表6 内嵌杉木与未嵌木材的毛竹连接试验对比Table 6 Comparison between two types of Moso Bamboo connections with or without Chinese fir

图9所示为螺杆变形图，其中内排螺杆变形很小，可以视作固定端。穿有钢板的外排螺杆中部挤压外侧杉木，螺帽部位挤压内侧杉木。外排螺杆同时受杉木两个方向的挤压力，其作用力等值反向，每处荷载分布长度可取为杉木直径的1/6。

图9 螺杆变形

在弯断前，螺杆的受力情况如图10(a)所示，其中Fu为试件极限拉力，由试验机施加，按50%极限荷载法考虑，其数值即为屈服荷载的2倍。由于连接受力的复杂性，对受力模型进行适当简化，如图10(b)，假定如下：

1)钢板上的力全部由竹壁承担，即单侧竹壁合力为Fb=F/2。

2)外排螺杆挤压杉木的作用力Fem为均布荷载且等值反向，其大小与Fb成比例，即Fem=αFb。

螺杆简化计算简图如图10(b)所示，根据螺杆受弯强度计算以及弯矩平衡，可得

(1)

再由实际受力以及计算假设可得

(2)

求解式(1)、式(2)可得

(3)

(4)

式中：fu为螺杆的极限强度,N/mm2；M为螺杆跨中所受最大弯矩,N·mm；W为螺杆抗弯截面系数,mm3；Fu为试件极限拉力,N，由试验机施加；D为毛竹外径,mm；t为毛竹壁厚,mm；d为螺杆直径,mm；Fy为连接屈服荷载,N；DW为内嵌杉木直径,mm；β为拟合参数，且其值为拟合值，与螺杆直径有关，对M8螺杆，β=0.081，对M10螺杆，β=0.065。

图10 螺杆弯断时的受力情况Fig.10 Loading condition of screw when

将试验结果与理论计算结果进行比较，结果如表7所示。试件实际屈服荷载与理论屈服荷载比值最大为1.09，最小为0.93，理论屈服荷载可以较准确地模拟试验屈服荷载。

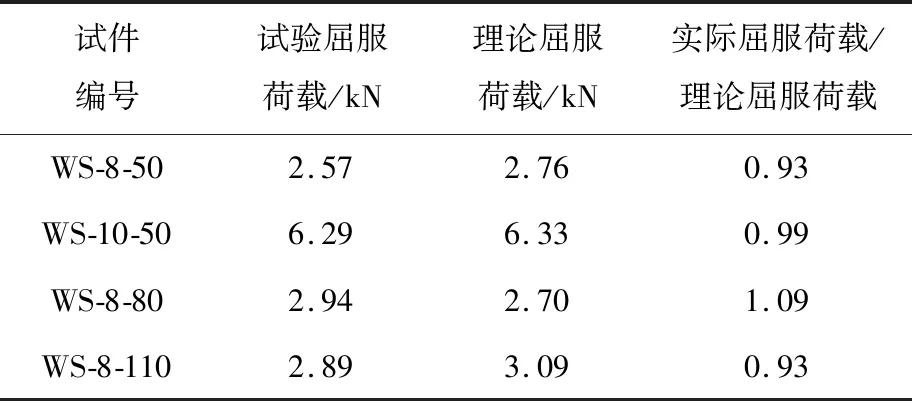
表7 螺杆弯坏试验值与理论值比较Table 7 Comparison of screw bending experimental and theoretical values

内嵌杉木的毛竹发生竹壁开裂破坏时存在一条开裂缝隙。由于分配在毛竹壁和杉木上的作用力大小不易获得，无法通过受力分析推导竹壁开裂破坏的计算公式。考虑到竹材与木材同属于生物材料，均是以木质纤维为主要构成成分，故对竹壁开裂的理论计算参考了Eurocode 5[16]中木材连接的计算公式，并引入计算系数，如式(5)所示。

(5)

式中：α为竹壁开裂计算系数，该系数为拟合参数，经拟合，本批竹材取1.79；My,Rk为螺杆弯曲破坏时的极限弯矩；fv为毛竹抗剪强度，本批竹材取12 MPa；t为毛竹壁厚。

按式(5)计算竹壁开裂时的屈服荷载，并将屈服荷载试验值与理论值进行比较，如表8所示，屈服荷载试验值与理论值的比值范围为0.91～1.09，误差均在10%以内，采用此公式可以较准确地计算内嵌杉木连接竹壁开裂的屈服荷载。

在发生竹壁剪出破坏时，毛竹孔壁承压导致毛竹产生两条剪出裂缝。同理，采用式(6)计算竹壁剪出屈服荷载，式中α1为毛竹剪出计算系数，为拟合参数，经拟合，本批竹材取1.67。

表8 竹壁开裂试验值与理论值比较Table 8 Comparison between test value and theoretical value of Moso Bamboos cracking

(6)

按式(6)计算连接竹壁剪出的理论屈服荷载，并将实际屈服荷载与理论屈服荷载进行比较，如表9所示，可见实际屈服荷载与理论屈服荷载比值范围为0.62～1.28，误差较大。除WS-14-50、WS-16-50外，其余试件的实际屈服荷载均大于理论屈服荷载，采用此计算方法进行计算，结果偏保守。其中，端距较小的试件可以通过控制端距最小值来避免连接发生竹壁剪出破坏。为了计算简便，竹壁剪出破坏的屈服荷载可以采用竹壁开裂的屈服荷载计算式进行计算。结果如表10所示，当控制螺杆端距不小于80 mm时，采用竹壁开裂计算式计算竹壁剪出破坏的屈服荷载，实际屈服荷载大于理论屈服荷载，且不大于理论屈服荷载的20%。故为了计算方便，竹壁开裂和竹壁剪出屈服荷载均采用式(5)计算。