土工格栅加筋碎石土动回弹模量及预估模型试验研究

2022-05-13张航周志刚韩健

土木与环境工程学报 2022年4期

张航，周志刚，韩健

(1.中交路桥建设有限公司，北京 100027；2.长沙理工大学道路结构与材料交通行业重点试验室，长沙 410004)

在现行沥青路面设计规范中，路基土的动回弹模量是重要的设计参数[1]。动回弹模量是指路基土体在动态荷载作用下产生的应力与其相应的回弹应变的比值，表示路基在弹性变形阶段内，在垂直荷载作用下抵抗竖向变形的能力。同时，加筋土技术因其适应性强、经济性好以及生态环保的特点，在许多现代道路工程中得到较为广泛的应用。诸多学者通过室内外试验研究表明，在路基中布设土工格栅之类的加筋材料有助于提高其回弹模量。如胡幼常等[2]利用强度仪法测定了掺砂黄土和土工格栅加筋黄土试样的回弹模量，结果表明，两种方法都能明显提高黄土的回弹模量，同时使用效果更佳；Abu-Farsakh等[3]开展了承载板试验，发现土工合成材料能使路面基层回弹模量显著提高；Kravchenko等[4]通过不排水三轴压缩试验，证明加筋试样的回弹模量要高于未加筋试样；罗正东等[5]研究了竹筋格栅加筋路基的承载变形机理，发现加筋能有效控制挖填路基的变形，对回弹模量提高产生一定的促进作用。

然而,上述方法均属于对土基静态回弹模量的研究，但路面上交通车辆对其施加的力都是动态的，所以对路基动回弹模量的研究意义更为重大，因此，学者们通过动三轴试验进行了更深入的探讨。如Fardad Amini等[6]利用循环三轴试验，基于能量法发现纤维加筋使砂土具有更高的循环抗剪能力；孙磊[7]针对路基软黏土开展循环动三轴加载试验，讨论了长期交通荷载下路基土回弹模量随动应力比的变化情况；杨果岳等[8]采用GDS振动三轴仪进行试验，得到了不同因素对超固结重塑红黏土动弹性模量的影响规律；刘维正等[9]通过路基土的动三轴试验，研究了含水率、压实度等对动回弹模量的影响。但是，动三轴试验中针对土工格栅加筋材料的讨论还有所欠缺，需要更加系统全面的研究。同时，在中国公路路基设计规范中指出，路基的动回弹模量由CBR强度通过经验公式换算得来[10]，但由此得到的动回弹模量往往误差较大，并且精度不是很高。

笔者利用土工试验动三轴系统，通过对不同含水率、加筋方式以及围压下的土工格栅加筋碎石土试件进行动三轴试验，测试动回弹模量，探究其影响因素和变化规律，并提出相应的土工格栅加筋碎石土动回弹模量的预估方法，为路面结构设计时确定路基土动回弹模量提供理论参考。

1 动三轴试验材料与方法

1.1 试验材料

1)筋材

加筋材料为湖北力特土工合成材料有限公司生产的高密度聚乙烯土工格栅RS90PE。参照新的土工格栅国家标准，采取窄条拉伸方式，使用多功能材料试验机进行性能测试[11]。其试验得到的物理力学指标如表1所示。

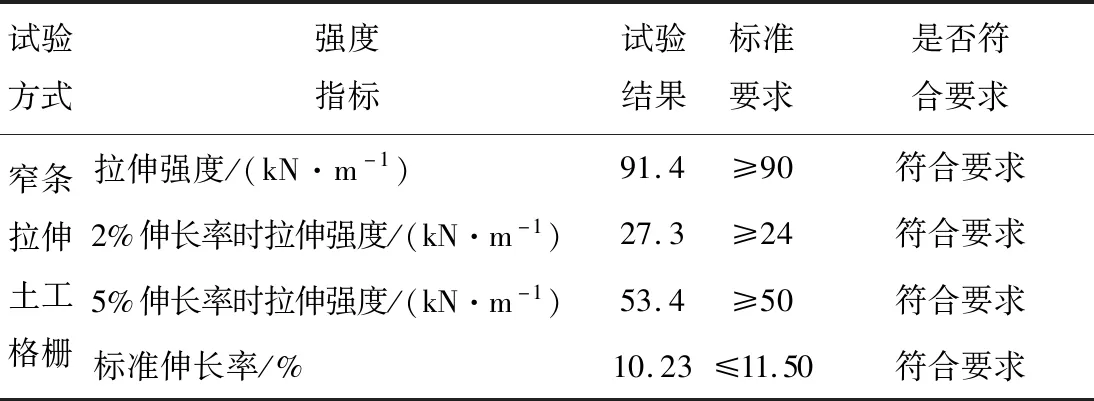
表1 土工格栅拉伸性能Table 1 Tensile properties of geogrid

2)填料

加筋土所用试验土的碎石含量约为63%，碎石粒径主要集中在5～20 mm之间。通过颗粒组成统计可知，该碎石土属于砾类土，d10=1.74、d30=4.58、d60=9.66，计算可得碎石土的不均匀系数Cu=5.56>5、Cc=1.25。所以，该碎石土易压密，级配良好。通过击实试验得到试验用碎石土的最佳含水量约为7.1%，最大干密度约为2.12 g/cm3。

1.2 试验方案

Seed等[12]在引入动回弹模量这一概念时，建议采用重复加载动三轴试验确定动回弹模量的值，并制定了相关的试验方法。在动三轴试验中，测定动回弹模量的方法是在一定的围压下对试件施加轴向动应力，循环施加至一定次数后，当动应变趋于稳定时测定最后几次的值来确定动回弹模量。

1)加载序列的确定

在用动三轴试验测定动回弹模量时需要确定试验加载序列。陈声凯等[13]在2006年建立了动三轴加载序列。对于碎石土之类的材料，所施加的动应力幅值应由小依次增大进行试验。对于土工格栅加筋碎石土动回弹模量的试验，其加载序列参考陈声凯等建立的加载序列，围压分别取50、100、150 kPa。具体加载序列情况如表2所示。

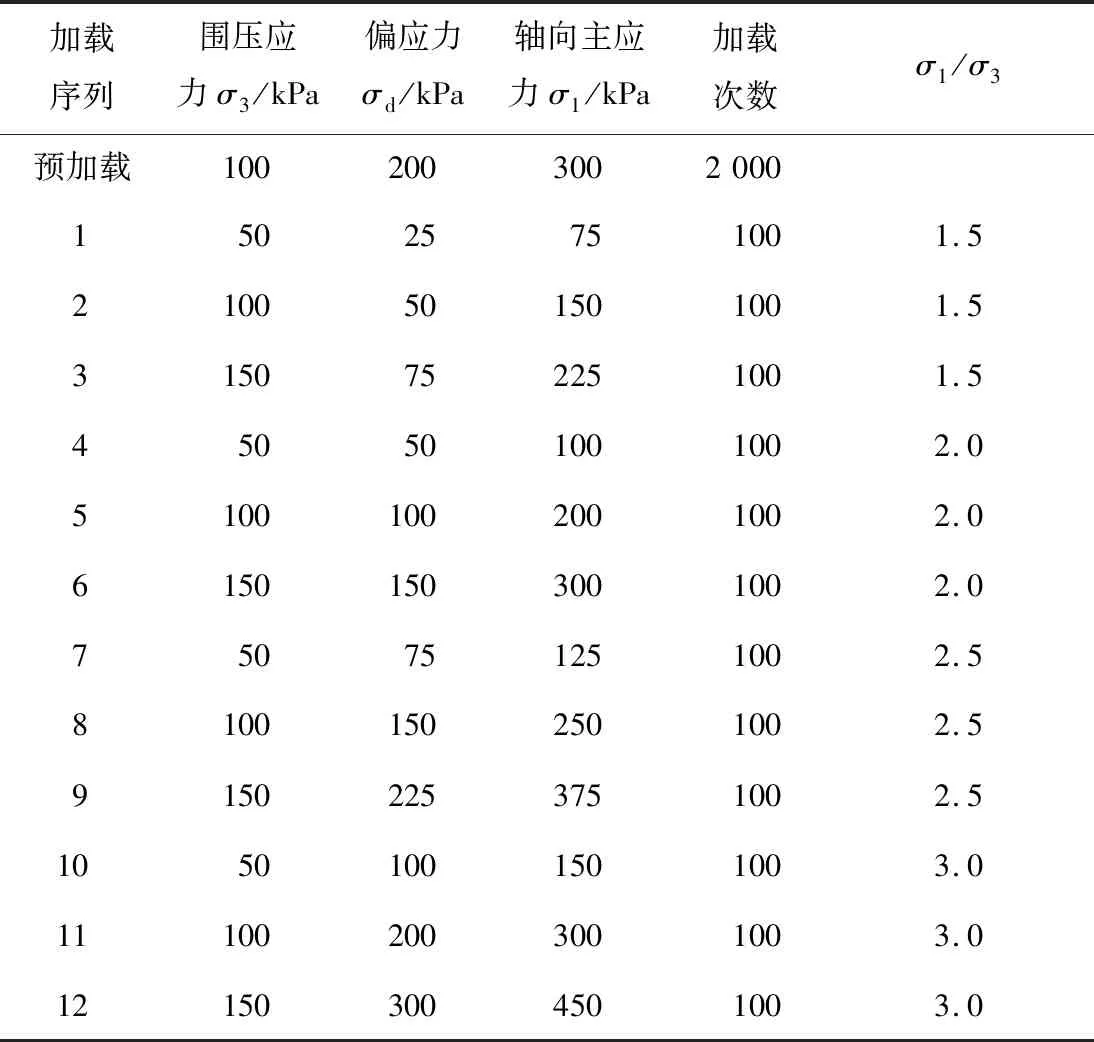
表2 土工格栅加筋土动回弹模量三轴测试方案加载序列Table 2 Load sequence of triaxial test scheme for dynamic resilience modulus of geogrid reinforced soil

在正式加载前先预加载，考虑到路基在施工期承受的荷载比运营期高很多，所以室内模拟试验的预加载比正式加载更严格。其他国家推荐的预加载次数为500～2 000次[14]，因此，试验预加载次数选取最大值2 000次。

2)加载波形的确定

试验循环动荷载的加载波形选择半正弦波，加载频率为1 Hz。在一个周期内，参照路面材料动三轴试验时加载0.1 s、间歇0.9 s的做法，考虑车轮荷载经过数十厘米厚的路面结构传递至路基顶面时影响范围更大，路基土受荷时间延长，故加载时间选为0.2 s，间歇时间选为0.8 s。

3)含水率的确定

研究表明，在给定的自然条件下，道路在运营期内其路基的含水率会从最佳含水率逐渐增大，并最终在与当地环境相适应的平衡含水率附近波动。Quintus等[15]通过对137条运营期道路路基含水率的现场调查，发现路基的含水率介于最佳含水率和150%最佳含水率之间。因此，试验的含水率定为100%最佳含水率、115%最佳含水率、130%最佳含水率。

4)加筋方式的确定

试验试件为圆柱形，试验加筋方式分为不加筋、加一层筋、加两层筋。其中，加一层筋时土工格栅放置于试件截面中心位置，加两层筋时土工格栅分别放置于距试件顶面和底面50 mm处。具体加筋方式如图1所示。

图1 加筋方式

1.3 试验过程

1)试验仪器

在动三轴试验中，试件采用静压成型，主要成型设备包括定制的对开模具和万能静压仪。试验加载系统采用深圳Reger公司定制的土工试验动三轴系统，该土工试验动三轴系统主要包括三大部分，分别是控制和数据采集软件系统、加载系统和围压应力提供系统。

2)试样制备

试件采用万能静压仪分层静压成型。每层填料的质量根据所取得的压实度控制。由压实度、干密度及试件的体积计算出所需的碎石土质量，试件分5层进行压实，每一层的质量一致，压实厚度一致，保证试件压实度均匀，试件最后一层静压结束后以恒载静压5 min。注意在压实过程中，每层压实完成后用铲刀将碎石土表面划槽。为了避免试件断裂，选择用专门尺寸的脱模机进行脱模。若脱模后不能及时用于试验，则先用塑料保鲜膜包裹好，防止水分蒸发。

3)试验操作基本步骤

安装试件，保证套好橡皮膜的试件置于三轴室中间位置，并插入传力杆，完成注水。通过围压控制器施加目标围压，当围压稳定后，再施加10 N的接触应力，接着选择加载次数和加载序列，进行加载试验。所有序列加载完毕后，依次抬起加载器，拔掉输水管，拧开排水阀，取出传力杆。待三轴室内部的水全部排出后，用扳手拧开螺丝，取下玻璃罩，取出试件，去除套在试件表面的橡胶膜，然后观察试件是否有明显的进水现象，如果进水比较明显则认为该次试验失败，应该重新制备试件再进行试验。

2 动回弹模量影响因素分析

根据上述试验方案，每种组合工况要求3组平行试件。利用动三轴试验，可以得到每组试件在重复荷载作用下变形稳定后的重复应力和此时的回弹应变，两者比值即为动回弹模量，可按式(1)计算。

(1)

式中：MR为动回弹模量；σd为轴向重复应力峰值，σd=σ1-σ3，σ1、σ3分别为最大主应力、最小主应力；εR为轴向回弹应变峰值。

对每个应力幅值的最后10次应力应变数据按上式进行处理，取平均值视为当前应力幅值下所对应的动回弹模量。每组平行试验结果与其均值相差均应不超过5%。

2.1 含水率对动回弹模量的影响

根据试验数据，绘制成图2～图4，分析比较试件含水率对动回弹模量的影响。

图2 不加筋时动回弹模量与偏应力关系曲线Fig.2 The relationship curves between dynamic elastic modulus and deviator stress without

图3 加一层筋时动回弹模量与偏应力关系曲线Fig.3 The relationship curves between dynamic elastic modulus and deviator stress when a layer of reinforcement is

图4 加两层筋时动回弹模量与偏应力关系曲线Fig.4 The relationship curves between dynamic elastic modulus and deviator stress when two layers of reinforcement are

由图2～图4可以看出，含水率对加筋土试件动回弹模量值的影响比较明显。在其他条件不变时，试件含水率越高则其动回弹模量值就越小。因为在碎石土中含有少量粘土，而其含水率越高，结合水膜厚度就越大，土颗粒之间的距离也越大，土体的内聚力和内摩擦角就越小，从而导致土体的抗压性能和抗剪强度的降低，水对土颗粒的润滑作用就越大。水对土工格栅与碎石土颗粒之间也有类似的影响。所以，在同一围压的应力幅值下，含水率越大，试件的变形就越大，从而导致其动回弹模量越小。

单独分析试件在加两层筋且在同一围压下其动回弹模量随含水率的变化情况。当含水率从最佳含水率增加到130%最佳含水率时：在50 kPa围压下，回弹模量下降了25.31%～32.31%，平均下降29.68%；在100 kPa围压下，回弹模量下降了28.54%～30.14%，平均下降29.57%；在150 kPa围压下，回弹模量下降了32.72%～34.56%，平均下降33.91%。

2.2 加筋方式对动回弹模量的影响

根据试验数据，绘制成图5～图7，分析比较试件不同加筋方式对动回弹模量的影响。

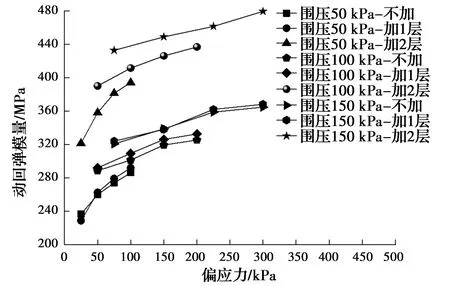
图5 100%最佳含水率下动回弹模量与偏应力关系曲线Fig.5 The relationship curves between dynamic resilience modulus and deviator stress under 100% optimal water

图6 115%最佳含水率下动回弹模量与偏应力关系曲线Fig.6 The relationship curves between dynamic resilience modulus and deviator stress under 115% optimal water

图7 130%最佳含水率下动回弹模量与偏应力关系曲线Fig.7 The relationship curves between dynamic resilience modulus and deviator stress under 130% optimal water

由图5～图7可以看出，当只加一层土工格栅时，试件动回弹模量基本没有发生变化，而当加了两层土工格栅时，与不加和加一层相比，动回弹模量明显增大。

在碎石土中加入土工格栅以后，在一定程度上会改变土体的整体刚度。在试验过程中，不加土工格栅和加一层土工格栅相比，动回弹模量值差别很小，是因为在进行动三轴试验时，由于试件上下结构和荷载的对称性，上下端部荷载传递至其中部时，横截面上难以形成水平剪切错动状态，此时即使在试件中部埋置了土工格栅，土工格栅与碎石土粒料之间也难以形成剪切嵌锁效应，与未埋置土工格栅的试件受力变形状态差别甚微，所以不加土工格栅和加一层土工格栅相比，其动回弹模量并没有什么变化。当加两层土工格栅时，即在距试件上下端面附近各加一层土工格栅，在试件端部施加的荷载传递至试件上下部的土工格栅位置时，产生了水平剪切错动行为，使得土工格栅与碎石土土体之间产生剪切嵌锁效应，约束了土体侧向变形，降低了轴向变形，增加了碎石土体刚度，从而导致在加了两层土工格栅后，试件的动回弹模量明显增大。由此可见，增加加筋层数或减少层间距，有利于动回弹模量的提高。

现单独分析试件在最佳含水率且在同一围压下其动回弹模量随加筋程度的变化情况。当试件由不加筋到加两层筋时：在50 kPa围压下，回弹模量增大了35.77%～39.17%，平均增大37.60%；在100 kPa围压下，回弹模量增大了33.40%～34.22%，平均增大34.81%；在150 kPa围压下，回弹模量增大了28.62%～34.93%，平均增大31.87%。

2.3 剪切影响表征量对动回弹模量的影响

在动三轴测土工格栅加筋土动回弹模量试验中，剪切影响表征量主要包括循环偏应力σd和八面体剪应力τoct，一般情况下，默认σ2=σ3且σ1=σd+σ3，所以

(2)

由此可见，循环偏应力对动回弹模量的影响与八面体剪应力一致。由图2～图7可以看出，当围压保持在一个固定数值时，测得的动回弹模量值随偏应力的增大而呈现非线性增大，同理，动回弹模量也是随八面体剪应力的增大而呈现非线性增大。分析原因可知，当围压保持不变时，随着循环偏应力的增大，试件的竖向变形也随着增大，但由于此时竖向变形及应变增大的幅值小于循环偏应力增大的幅值，所以此时试件的动回弹模量是呈现增大趋势的。

单独分析在最佳含水率且加两层筋时，试件动回弹模量随循环偏应力的变化情况。在50 kPa围压下，当偏应力由25 kPa增大到100 kPa时，回弹模量增大了3.32%～11.41%，平均增大7.08%；在100 kPa围压下，当偏应力由50 kPa增大到200 kPa时，回弹模量增大了2.50%～5.47%，平均增大3.85%；在150 kPa围压下，当偏应力由75 kPa增大到300 kPa时，回弹模量增大了2.82%～3.90%，平均增大3.47%。

2.4 侧限影响表征量对动回弹模量的影响

在动三轴测土工格栅加筋土动回弹模量试验中，侧限影响表征量主要包括围压应力σ3和体应力θ，其中，体应力又称第一应力不变量且θ=σ1+σ2+σ3。根据众多学者研究发现，在侧限影响表征量中，体应力θ对动回弹模量的表征效果要好于围压应力σ3。其内在机理为：在循环偏应力保持不变时，随着围压的增加，动回弹模量值也会随之增加。这是因为随着围压的增大，侧限作用力的增大会使试件的竖向变形减小，即应变减小，则在循环偏应力不变的情况下，动回弹模量值增大。因为一般情况下默认σ2=σ3且σ1=σd+σ3，所以经过化简后体应力θ=3σ3+σd，由此可见，体应力θ不仅考虑围压应力对动回弹模量的影响，还考虑了循环偏应力变化带来的影响，故体应力θ能更好地表征动回弹模量的变化，其是具有普适性的。在分析体应力对动回弹模量的影响时，分别考虑试件在不加筋、加一层筋和加两层筋时，其动回弹模量随体应力的变化情况，整理数据，绘制成图8～图10。

图8 不加筋时动回弹模量与体应力关系曲线Fig.8 The relationship curves between dynamic elastic modulus and body stress without

图9 加一层筋时动回弹模量与体应力关系曲线Fig.9 The relationship curves between dynamic elastic modulus and body stress when a layer of reinforcement is

图10 加两层筋时动回弹模量与体应力关系曲线Fig.10 The relationship curves between dynamic elastic modulus and body stress when two layers of reinforcement

从上图可以看出，在同一围压、同一含水率下，加筋土试件的动回弹模量是随着体应力的增大而增大的。其增大情况与同一围压、同一含水率下，加筋土试件的动回弹模量随着偏应力的增大情况保持一致。

3 动回弹模量预估模型研究

为了提供路面结构设计时所需的路基动回弹模量的确定方法，选用NCHRP 1-28A推荐的模量预估模型(见式(3))，NCHRP 1-28A模型既考虑了剪切影响表征量对动回弹模量的影响，也考虑了侧限影响表征量对动回弹模量的影响，可以更加全面地反映各种应力对动回弹模量的影响，并且美国国有公路运输管理协会也推荐使用该模型进行回归[16]。针对不同加筋方式、不同含水率下的碎石土动回弹模量试验结果，利用Origin软件的多元非线性回归分析进行处理，得到相应的模型参数值，如表3所示。

(3)

式中：Pa为大气气压，一般取100 kPa；θ为第一应力不变量；τoct为八面体剪应力；k1、k2、k3为回归参数。

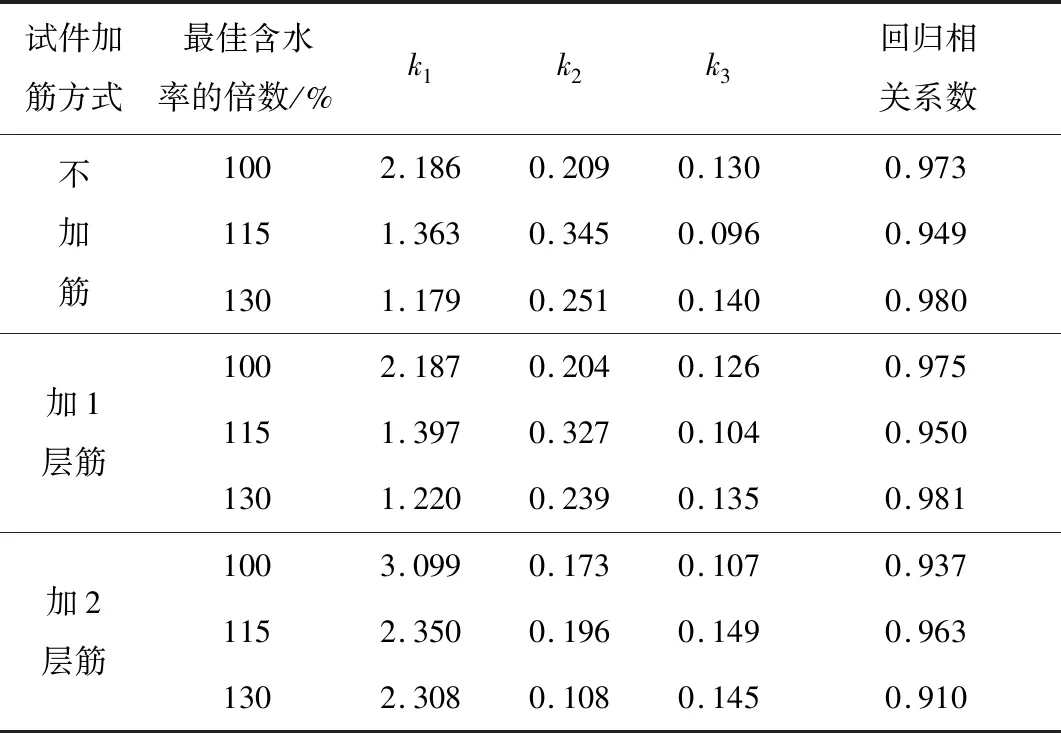
表3 加筋土动回弹模量预估模型参数回归结果Table 3 The parameter regression results of the prediction model of dynamic resilience modulus of reinforced soil

回归拟合结果的好坏通常用相关系数R2来表示，当得到的R2接近于1时表示拟合结果较好。从上表可以看出，动三轴试验经数据回归后得到的相关系数R2比较接近于1，说明NCHRP 1-28A模型具有较高的合理性。具体分析上表中的模型参数值时可以发现：k1值的规律性比较强，当试件的加筋方式保持不变时，其值随着含水率的增加而减小，并且由100%最佳含水率到115%最佳含水率的减小幅度较大；k2值也具有一定的规律性，当试件的加筋方式保持不变时，其值随着含水率的增加呈现出先增大后减小的趋势；整体来看，k3值的规律性并不强，之前k3的经验值往往为负值，但试验数据回归出来的k3为正值，这可能跟材料本身的性能有关，因为碎石土试件在发生塑性变形后易发生应变硬化现象，同时加筋后的筋材对土体变形起到了一定的约束作用，所以动回弹模量与八面体剪应力呈现出了正相关的趋势。