主从同步晶振频率误差的卡尔曼收敛算法

邓长顺，牛兰杰，黄 辉

(西安机电信息技术研究所,陕西 西安 710065)

0 引言

弹药组网技术具有广阔的使用场景，战场环境下高动态平台和武器间的关系往往无法预先规划，系统应具有自组织网络特性[1]。无线自组网(wireless ad-hoc network)能在陆、海、空基作战系统上应用，对于机动协同作战有重要意义[2]。这使得高动态协同攻击对无线组网时间同步精度控制提出了更高要求，时间一致性对提高信息时效性及协同毁伤效能至关重要，所以时间同步精度是组网的关键指标。

无线组网时间同步算法优化趋势：1) 分析并降低同步消息交换过程中的各类时延，实现同步精度的提高；2) 引入分簇思想对网络拓扑改进，在多跳网络中有效克服误差随跳距增大而累计的缺陷且平衡网络能量消耗，可上升至MAC层路由算法层面；3) 融入线性拟合等数学理论，对同步数据进行计算调整[3]。近期学者提出双向交互同步算法(timing-sync protocol for sensor network，TPSN)，从路由角度入手软件控制，对网络拓扑进行层级划分，逐层进行时间同步实现全局同步，是分簇思想的代表[4]；文献[5]在增强无线传感器网络时间同步中提出了低功耗组网时统方法，单从低频晶体降低能耗分析；文献[6]在论文中研究卫星同步高稳晶振的影响，但对采样噪声考虑较少。

本文针对当前高动态无线平台时间控制精度要求较高，现有时间同步算法忽略了无线信道数据包冲突导致的硬件物理时钟延迟抖动及时间戳的采集等噪声影响，提出基于主从同步晶振频率误差的卡尔曼收敛算法。

1 无线组网时间同步架构

1.1 无线组网时间同步层次划分

时间同步是指在分布式系统中，物理上彼此独立的节点为了保持时间一致性，通过无线通信协议(如时分多址TDMA)将本地时钟调整到统一时间点的过程。无线自组网大多基于报文传输同步信息的协议都面临传输过程中的不确定性，有些不确定时间误差可能高于系统要求的同步精度。无线组网收发分解示意图见图1[7]。

图1 同步数据收发分解示意图Fig.1 Schematic diagram of synchronous data sending and receiving decomposition

信道接入时间是收发过程中传输时延中波动性最大的一部分，消息等待信道空闲所需时间，取决于MAC协议和网络负载状况。节点从应用层发出数据包，到接收方应用层收到数据包，每一层之间都存在着一定的噪声和误差，越靠近物理层输出的时间戳标记误差波动越小，通讯过程中协议设计收发数据包的双方在MAC层标记时间戳[8]，然后交换各自时间戳后进行统计再根据同步算法调整本地时钟，两个节点完成一次“时间握手”。开放式通信系统互联参考模型(open system interconnection)，是国际标准化组织(ISO)提出的一个使各种计算机在世界范围内互连为网络的标准框架，简称OSI[9]。主要包括七层，如图2(a)，本文组网架构层次如图2(b)所示。

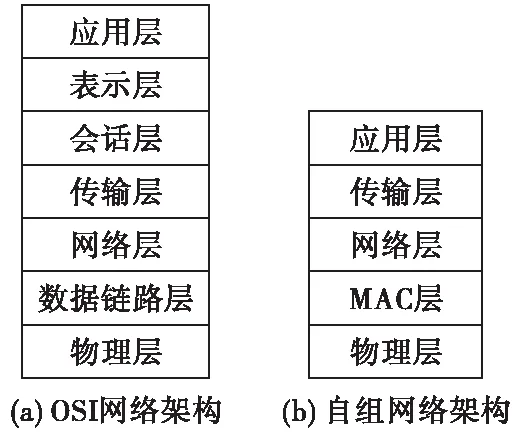
图2 网络架构层次Fig.2 Architecture hierarchy of network

1.2 硬件时钟物理建模

从物理角度来看，由于节点的石英晶体振荡频率不是恒定的，温度、辐射等会造成节点的本地硬件模拟时钟出现抖动和偏移，导致软件时钟发生频率漂移和时钟偏移，所以时间同步需将不同节点内的晶振频率收敛到一个基准点。节点是通过晶体谐振器(如图3所示)和振荡器自身组装的中断进行计数来实现的，频率可通过如温补晶振、改变负载电容CL来调整频率输出。每秒产生中断计数的值理想状态是不变的，晶体初始定值和频率误差不同，长期稳定性不好。图4为硬件时钟过慢(或过快)和时钟漂移与本地标准时钟的差异。

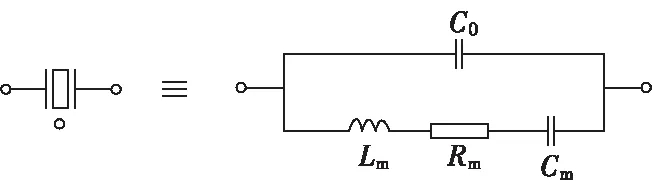
图3 晶体谐振器模型Fig.3 Crystal resonator model

图4 时钟误差模型Fig.4 Clock error model

定义T为实际物理时间，T(t)为节点的本地时间。理想时钟的时间变化率等于常数1。由于晶体振荡器存在一定的漂移，可定义的时间变化率为f(t)=dC(t)/dt，节点i局部时间Ti(t)从物理时间t0到t的变化可用式(1)表示，ψi(t0)为节点i在物理时刻t0的初始相位值。

(1)

式(1)通过泰勒级数展开为以下方程：

Ti(t)=βi+αit+γit2+…，

(2)

式(2)中，βi和αi分别代表实际物理时间t的初始相位偏移和频率偏移。若式(2)中二次项以上系数均为0，则可简化为线性预测时钟模型，近似为:

Ti(t)=βi+αit。

(3)

基于式(3)描述的线性时钟模型，时钟关系取决于时钟频率参数αi和初始相位参数βi。节点启动时，参数βi被抑制短时间不变，而参数αi随着时间变化而变化，这主要是由晶体振荡器的漂移效用引起的。根据式(3)，节点A和B之间的时钟关系可以表示为：

TB(t)=βAB+αAB·TA(t)，

(4)

式(4)中，βAB和αAB分别表示节点A相对节点B之间的相位偏移和频率偏移。当βAB=0和αAB=1时，节点A和节点B可以实现时钟同步。而当βAB≠0和αAB≠1时，这两个参数随时间的积累变化，会产生如表1的结果。

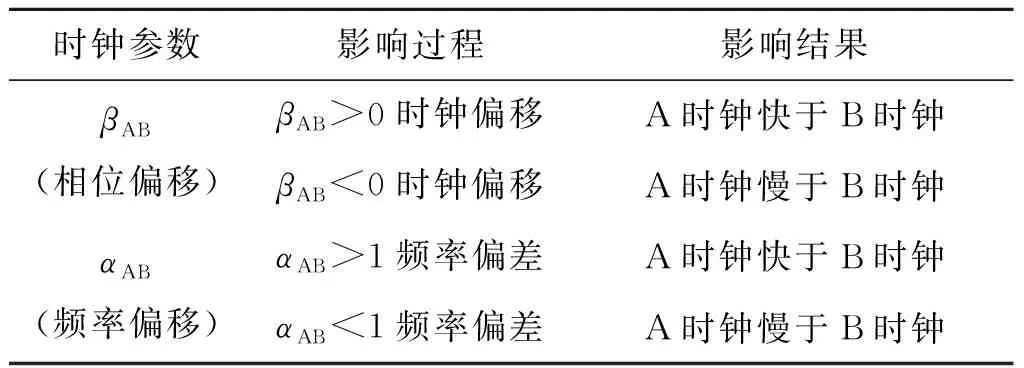
表1 时钟参数变化影响Tab.1 Impact of clock parameter changes

1.3 主从同步周期时间步骤

基于主从同步周期的运行步骤如图5所示。

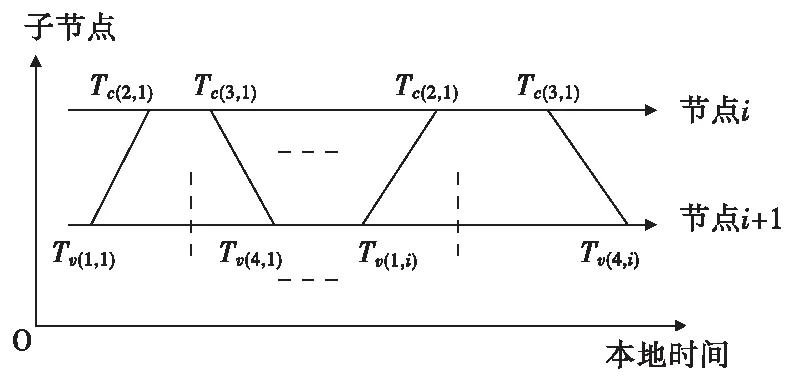
图5 子节点时钟同步模型Fig.5 Child node clock synchronization model

基于上述模型可分析两个节点之间的时延与频偏参数：

(5)

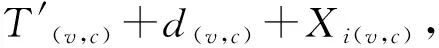
(6)

式(5)、式(6)中，w表示时间偏移率，T′表示相位偏差，d为传输噪声误差，X为外部随机噪声时延。经多次同步过程后，若不考虑各类误差，可以进一步估算k时刻两个节点之间的时间偏移量T(k)与时间偏移率W(k)：

T(k)=[(Tc(2,k)-Tv(1,k))-(Tv(4,k)-TC(3,k))]/2，

(7)

W(k)=[T(k)-T(k-1)]/Δt。

(8)

2 主从同步晶振频率误差卡尔曼收敛 算法

线性滤波预测理论，是在线性状态空间的基础上对噪声和观测信号进行处理：系统内部扰动和观测噪声对它们的统计性质作适当假定，对含噪声的观测信号进行状态观测反馈。状态反馈器工作模式：x为系统输入值，Y为输出的真实测量值，测量误差会影响其准确性，y′为输出变量的估计值。状态变量的真实值通过状态观测器对估计值与系统测量值(含噪音)进行比较输出后经回路K反馈，对未知状态估计进行校正后得到一个可靠状态估计值。

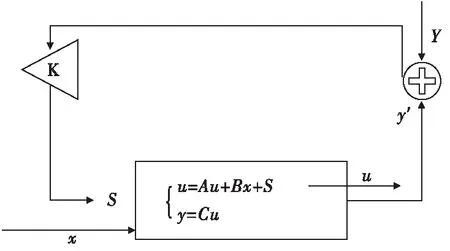
图6 状态观测器Fig.6 Status observer

由于子节点初始化具有随机性，时钟初始相位是不同的，将节点相位之间的差值称之为时钟偏移(offset)，同时称晶体振荡器实际工作频率与额定频率之间存在的偏差为时钟偏移率。同步过程中，节点的时钟偏移率会随着时间不断累积，最终使节点间产生较大的时钟偏移。因此需周期性地对节点进行校验，保证时间同步误差在可控范围内。基于主从时间同步及对理论时钟模型变量分析，根据卡尔曼滤波运动学原理，设计了图7的算法流程图，通过对之前的时间统计，各种噪音(频率噪声、随机噪声等)的估计输入进行滤波，逐渐贴近真实时间戳输出值，提高系统的时间同步精度。

图7 主从同步晶振频率误差卡尔曼收敛算法流程图Fig.7 Master-slave synchronous crystal oscillator frequency error Kalman convergence algorithm flowchart

2.1 时间同步状态转移

状态转移是根据观测数据对随机量进行定量推断，动态行为的状态估计能实现实时运行状态的估计和预测。式(9)为通常状态下的卡尔曼滤波状态转移方程，式(10)为参数协方差转移矩阵。

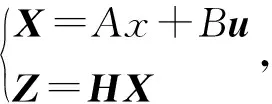
(9)

P=APAT+Q。

(10)

在时间同步系统中，X为时延参数矩阵，含时间偏移以及时间偏移率，A和B是系统参数，对于多模型系统时为矩阵。H为参数测量转换矩阵，系统过程Z和测量的噪声被假设成高斯白噪声，它们的协方差(covariance)分别是Q，R。对于主从时间同步系统，将式(5)与式(6)作差可得式(11)，推导得到时间同步状态转移方程(13)：

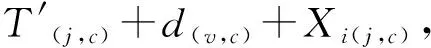
(11)

T=HX+S，

(12)

Tk=Tk-1+Δt·Wk-1，

(13)

Wk=Wk-1，

(14)

式(12)是节点时延的向量表达，T为时延参数，S为观测噪声如振荡器内部噪声误差等。X选用主从时钟的偏移量T和时钟偏移率W为状态变量，对时钟进行数学建模，推导可得时间同步的状态观测转移矩阵：

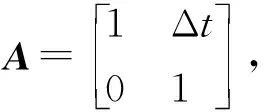
(15)

式(15)中，Δt为时间同步周期。

2.2 基于卡尔曼滤波的主从时间估计同步算法

分析可知，实际描述的系统传输状态转移延迟抖动较大，存在环境等观测噪声干扰，且时间戳获取存在误差，故采用卡尔曼滤波，估计这些误差的影响后在同步过程中消除。该算法具体操作步骤为：预测过程，X(k)是k时刻下的系统状态，A为系统参数观测转移矩阵，B为时间同步控制矩阵，u为同步校正矩阵，L为过程状态噪声。

X(k|k-1)=A·x(k-1)+B·u(k-1)+L。

(16)

最小预测协方差矩阵为P(k|k-1)，可以初始化为Q：

P(k|k-1)=AP(k-1)AT+Q

(17)

在卡尔曼滤波中的时间同步卡尔曼增益矩阵为：

K(k)=P(k|k-1)HT[HP(k|k-1)HT+R]-1

(18)

综合考虑时间戳参数与噪声影响，得到状态修正式(19)。可利用估计得到的主从时钟偏移量估计量对时钟模型进行修正，从而提高时钟同步精度。

X(k|k)=X(k|k-1)+K(k)[z(k)-HX(k|k-1)]。

(19)

P(k|k-1)是X(k|k-1)对应的协方差，AT表示A的转置矩阵，Q是系统过程的协方差，H为观测量转换矩阵。得到k状态下最优的估算值X(k|k)，但是为了要令卡尔曼滤波器不断运行下去直到系统过程结束，还要更新k状态下X(k|k)的协方差：

P(k)=(I-K(k)H)P(k|k-1)。

(20)

通过上述系统迭代公式对于时间戳估计误差的两个关键参数时间偏移和时间偏移率作出了跟踪估计，使之与真实偏差收敛到最小。子节点根据估计的时间偏移和时间偏移率作出调整，并将新的时间参数输入到系统中进行迭代，达到时间同步目的。

3 基于算法的仿真实验验证

为了验证本算法对于节点时钟同步精度的提高，分别对时间偏移和时间偏移率的跟踪消除，根据第2章介绍的算法使用Matlab软件进行仿真。本实验采用卡尔曼滤波，综合节点的物理时钟特性，且考虑测量、过程噪声等因素的影响来验证本算法。

3.1 仿真实验子节点参数

本仿真实验的子节点参数设置：硬件时钟理论误差很小，大多数硬件时钟的频率都在10～50 MHz，所对应的理论时钟精度是在纳秒级别。但评价时钟源性能的指标包括频率准确度(在标称电压、标称负载、基准温度，晶体振荡器的频率相对于其规定标称的最大允许偏差，公式换算：时钟偏移率=频率偏移/标称频率=(fmax-fmin)/f0)以及频率稳定度(在规定温度范围内晶体振荡器输出频率的最大变化量相对于温度范围内输出频率极值之和的允许频偏值)[13]。温补晶振及恒温晶振是通过对温度特性进行补偿或者构建恒温环境以分别达到±0.01及±0.001级别的频率稳定度[14]。频率准确度上，普通的晶体振荡器一般在±50 ppm以内，即对于标称频率为10 MHz的石英晶体而言，其实际频率与标称频率的差别不超过±500 Hz，即两个标称频率相同的晶体振荡器每秒最大可能时钟偏移为100 μs。图8为基于主从同步模型的子节点时钟模型。

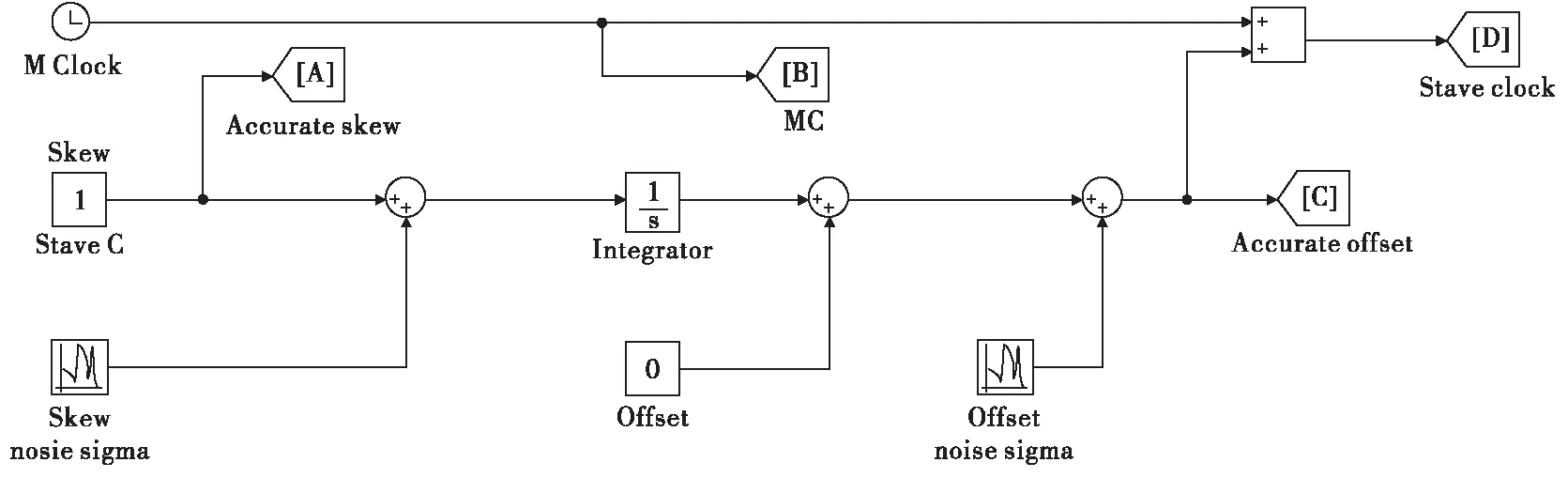
图8 子节点时钟同步模型Fig.8 Child node clock synchronization model

3.2 本文滤波估计算法仿真实验

3.2.1算法有效性验证

在基于卡尔曼滤波估计时间同步算法中，根据晶振参数与时钟偏移的模型特性，将初始的时间偏移offset设为100 μs，将初始的时钟偏移率drift设为50 ppm；采样次数为100次，进行卡尔曼滤波时间估计同步次数为40次来进行仿真验证，各类噪声设定为高斯白噪声。每进行一次滤波后，对从时钟进行精度调制，再次测量后输出。

由于延迟抖动以及获取时间戳带来的各类噪声误差，系统经过卡尔曼滤波的估计值会在真实值附近震荡，存在一定的误差，可利用估计得到的主从时钟偏移估计量以及估计时钟偏移率对子节点时钟模型进行修正，从而提高时钟同步精度。从仿真数据图9—图11看出，经过卡尔曼滤波约20次迭代后，时钟偏差的差值可稳定控制在±3 μs以内，频率偏移率经过约20次迭代后稳定控制在差值±3 ppm以内。由图12统计同步后采样点的偏差分布，可以看出经过40次迭代同步后偏移分布与偏移率分布大致符合均值为0的一个高斯分布，offset在0.259 3 μs、drift在0.018 8附近震荡。综合计算考虑，对于自组网时间同步精度可由百微秒级别提升至十微秒以内量级，且消除了一些噪声。

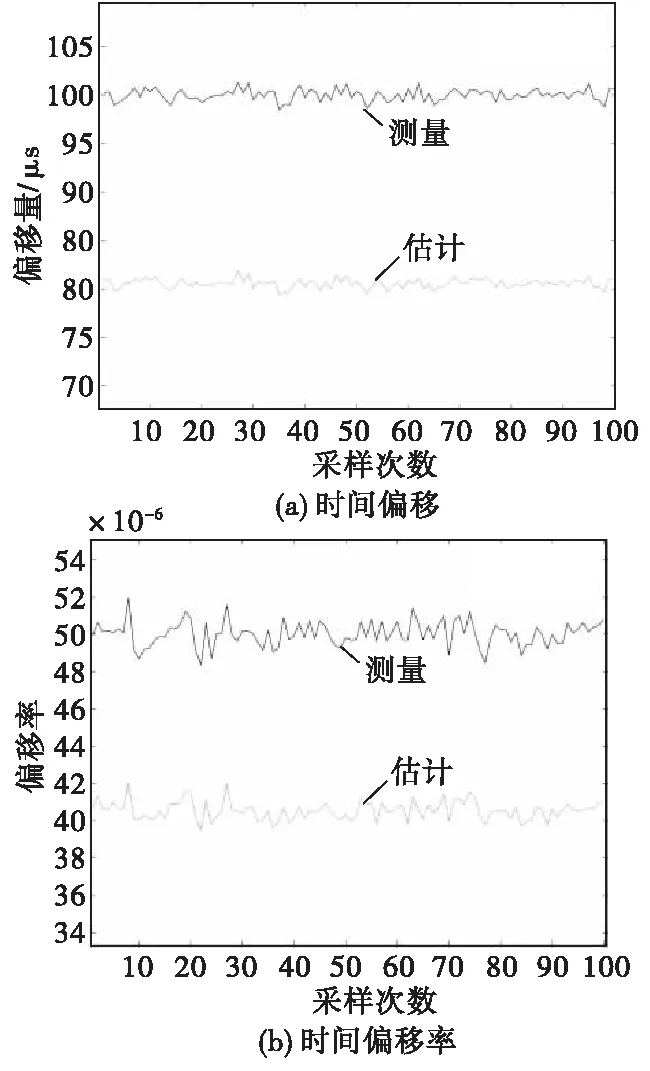
图9 时间偏移与时间偏移率第一次同步后的效果Fig.9 Time offset and time offset rate after the first synchronization

3.2.2算法可靠性分析

仿真基于算法模型增大时间偏移与时间偏移率后分别进行了运算分析，随着运算次数的增多，增加到1 000 μs误差级别也逐渐稳定在20～40多次以内迭代同步。滤波各步都在同一个运算级范围内，说明多次运算不会严重影响组网同步信息处理的实时性；且控制迭代次数有限的情况下(20次)，逐步增大输入偏差，其最终输出偏差均值可稳定在5 μs以内(见图12)，符合我们的同步精度提升要求。

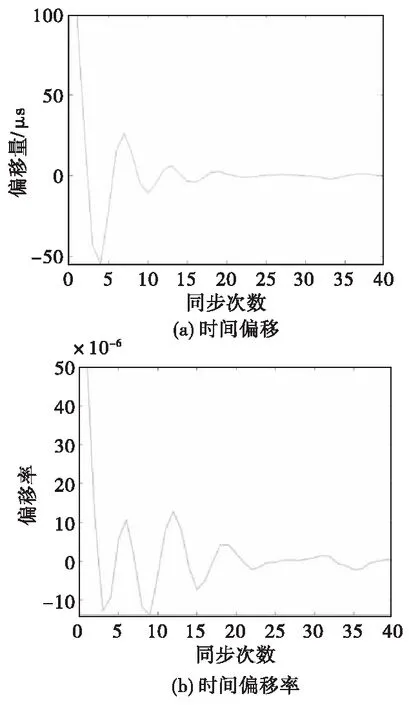
图10 时间偏移与时间偏移率随同步次数的变化Fig.10 Time offset and time offset rate vary with the number of synchronization times

图11 同步完成后时间偏移与时间 偏移率采样点统计分布Fig.11 Statistical distribution of time offset and time offset rate at sampling points after synchronization

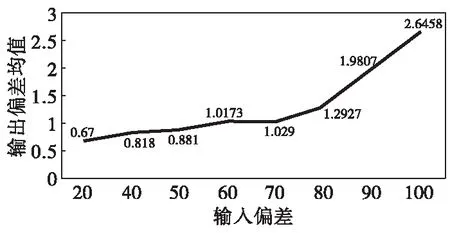
图12 输入偏差值经过有限次迭代后与输出均值的关系Fig.12 The relationship of the input deviation value to the mean output deviation after a finite number of iterations

通过调整观测噪声与过程状态噪声，探寻算法的噪声适应边界条件：仿真中对观测噪声与过程状态噪声标准差设定从1逐步增大到5，同步100次后，最终偏移收敛但方差仍较大，如图13所示，综合造成的时间偏移仍有数十微秒，无法满足所需同步精度提升量级。从数据侧面也能看出观测噪声相比过程噪声的影响更大，本算法对抑制噪声有一定的能力，但当观测噪声与过程状态噪声影响过大时，未能达到预想的同步效果。

图13 观测噪声与过程噪声方差对offset 与drift方差影响Fig.13 Observe the variances of noise and process noise on the variances of offer and drift

综上，将硬件晶振的物理模型转化为数学模型，经过卡尔曼滤波并对同步过程中的各类噪声加以分析，子节点时间戳统计量随着多次迭代时间偏移量逐步降低。通过卡尔曼滤波消除了一些难以避免的由于无线信道数据包碰撞导致的各类噪声与抖动误差的影响，将组网的时统精度控制提高一个数量级。

4 结论

本文提出基于主从同步的卡尔曼滤波晶振频率收敛算法。该算法利用卡尔曼滤波对于主从节点无线组网进行时间戳统计估计，并考虑过程及观测噪声影响，对物理硬件时钟晶振频率参数处理，分析时间偏移与时间偏移率参数随多次仿真同步的收敛规律。仿真实验验证结果表明，经过卡尔曼滤波时间估计后，在有限的同步次数下，时间同步精度可从百微秒量级提升至十微秒以内，同步精度方差稳定在1以内，有效降低了晶振频率偏差对时间同步精度的影响。本方法在无线组网硬件设计实现还具有很大的实践空间，可以进一步调试滤波器对于多节点组网时延精度以及功耗的影响。