引信离心球自毁机构作用动力学建模与仿真
2022-05-13王雨时张志彪
刘 宣,闻 泉,王雨时,张志彪
(南京理工大学机械工程学院,江苏 南京 210094)
0 引言
引信离心球自毁机构是利用弹丸转速在弹道上的衰减来控制自毁时间的一种机械自毁机构,在国内外已得到了广泛应用[1-9],其自毁锥面锥角不仅是决定自毁时间的关键因素,而且还对自毁发火时的戳击能量进而对发火可靠性产生影响。自毁锥面锥角是进行引信离心球自毁机构设计的重要参数,如何对该参数进行取值和优化,引信领域不少研究者对这个问题进行了多方面的探讨。文献[10—12]分析了离心球自毁机构自毁运动的动态特性,得到了临界自毁角速度的表达式,虽然对发火能量也进行了分析计算,但并未涉及自毁锥面锥角的设计优化问题。文献[13]给出了机构不出现自锁时自毁锥面锥角的取值范围,但也未涉及离心球自毁机构自毁锥面锥角对自毁发火时戳击能量和发火可靠性的影响。
自毁时间和自毁发火能量是引信离心球自毁机构的主要特性。影响引信离心球自毁机构自毁时间和自毁发火能量的因素有很多,包括自毁锥面锥角、自毁簧刚度和预压量、离心球离心半径、离心球质量(密度)、离心球半径及数量、自毁发火戳击行程等。在弹道参数不变的情况下,临界自毁角速度公式[12]可以作为自毁时间的衡量准则。在自毁时间不变的前提下,本文从理论上研究自毁锥面锥角对自毁发火能量和可靠性的影响,并结合算例利用ADAMS软件进行仿真验证,为引信离心球自毁机构自毁锥面锥角优化设计提供参考。
1 离心球自毁机构组成与原理
以瑞士35 mm高射炮榴弹KZVD(KZD242)引信为例对离心球自毁机构组成与原理进行简要分析,其自毁采用离心球自毁机构,如图1所示。
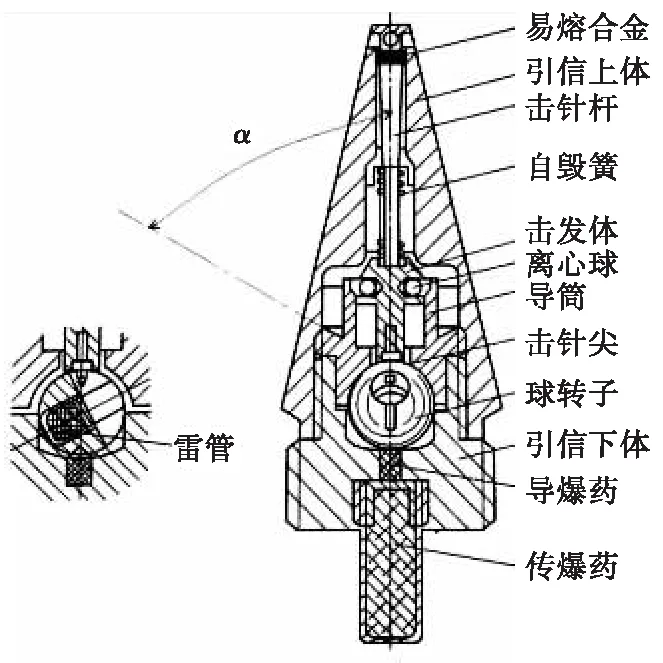
图1 瑞士KZVD引信离心球自毁机构Fig.1 Fuze centrifugal self-destroying device of KZVD of Switzerland
平时,自毁簧紧压着击发体,击发体又紧压着球转子,同时击发体上装的击针尖锁在球转子上的孔内,因而球转子不能转动。这时,击针尖与雷管错开一个角度,雷管又与导爆药错开一个角度,引信处于安全和隔爆状态。
发射时,击发体内的离心球在离心力的作用下向外甩,作用于导筒的斜面上。弹丸出炮口后,由于高速运动在引信顶部产生的阻滞温度使易熔合金熔化,熔化的合金被推开,自毁簧受离心球与导筒斜面作用的分力而被压缩。同时,击发体带击针尖上升,释放球转子,当转到与击针和传爆管对正的位置时,引信处于待发状态。
引信未命中目标时,在飞行过程中转速不断减小。当弹丸转速减小到特定值时,离心球离心力使击针杆向上运动的力就会小于被压缩的自毁簧的抗力。结果,自毁簧推动击发体向下运动,使击针尖戳击雷管而发火,实现自毁。
2 引信离心球自毁机构自毁作用动力 学分析
为了对引信离心球自毁机构自毁锥面锥角进行优化分析,则需要建立引信离心球自毁机构自毁作用的理论模型和各变量间的关系。
引信离心球自毁机构自毁过程可分为两个阶段:把离心球沿自毁锥面的运动作为第一阶段;把离心球沿导筒内孔圆柱面的运动作为第二阶段。
为分析引信离心球自毁机构动态过程并得到自毁发火能量,对引信离心球自毁机构系统作如下假设:1) 离心球、击发体(含击针)、击发体座及引信体等零件在自毁过程中均为刚体;2) 击发体(含击针)、击发体座及引信体同轴,且无相对转动;3) 忽略较小的爬行力和章动力影响;4) 在自毁过程中,弹簧抗力变化是均匀的,以考虑弹簧分布质量对自毁发火能量影响;5) 在整个自毁过程中,近似认为弹丸转速不变,即始终保持临界自毁角速度值。
2.1 离心球沿自毁锥面运动的动力学分析
根据引信离心球运动的不同形式,可将离心球自毁机构自毁运动分为3种方式:第一种为离心球沿自毁斜面作纯滚动,而在击发体上的球孔内滑动;第二种为离心球在球架上的球孔内作纯滚动,而沿自毁斜面滑动;第三种为离心球在自毁斜面和击发体上的球孔内既滚动又滑动[14-15]。文献[13]指出引信设计实践中多按离心球沿自毁锥面纯滚动而在击发体离心球孔内滑动的自毁运动方式,本文同样采用该种自毁运动方式进行动态特性分析。
建立直角坐标系Oxyz、O1x1y1z1以及O2x2y2z2,如图2所示。其中O1为离心球球心,O2为击发体质心,Oy轴为弹丸暨引信几何轴线,也是旋转轴线;O1x1轴沿O1至Oy轴垂直方向,O1y1轴平行于Oy;O1z1方向由右手法则确定;O2y2轴为击发体几何轴线,也平行于Oy;Ox轴平行于O1x1轴、O2x2轴。设A点为离心球与自毁锥面接触点,B点为离心球与击发体离心球孔接触点,C点为击发体与导筒接触点(假设C点与O2点、弹丸旋转轴线在同一平面O2x2y2内),D点为击发体离心球孔与离心球接触点(接触时B点与D点重合),E点为击发体与自毁簧接触点;r为初始位置离心球球心相对于弹丸旋转轴线偏心距;b为击发体几何轴线相对于弹丸旋转轴线偏心距;α为引信离心球自毁机构自毁锥面与几何轴线的夹角,即自毁锥面锥角的一半(因为文中锥角全部都是用α来描述且为表达方便,将α角称作锥角)。
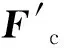
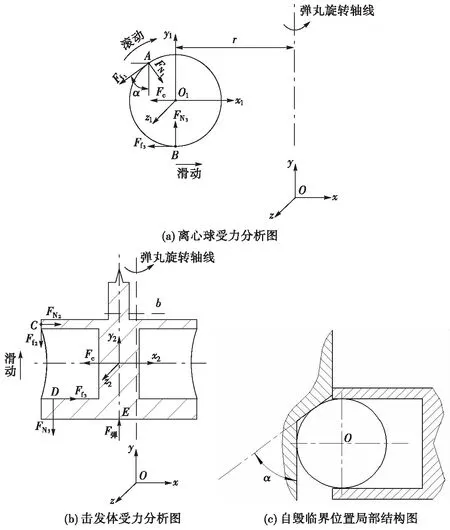
图2 离心球和击发体受力分析及自毁临界位置局部结构图Fig.2 Stress analysis of centrifugal ball and firing body and local structure of self-destroying critical position
由引信离心球自毁机构系统运动特性可知,离心球、击发体和自毁簧组成的系统动能
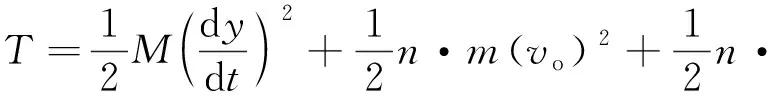
(1)
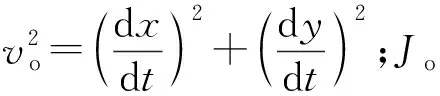
(2)
由Lagrange第二类方程
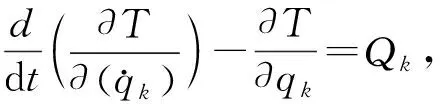
(k=1,2,…,N)
(3)
式(3)中,Qk为广义力,qk为广义坐标。把相关关系式代入上式得到系统运动微分方程
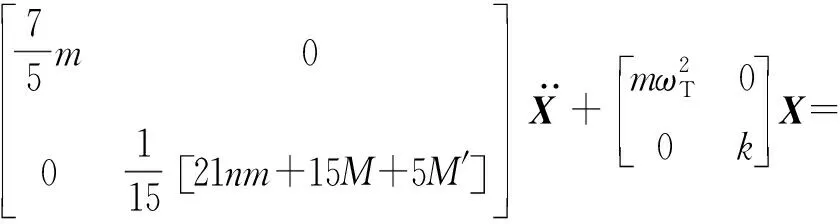
(4)
式(4)中,ωT为引信离心球自毁机构临界自毁角速度[9],λ为离心球与自毁锥面相切初始位置自毁簧压缩量,k为自毁簧刚度系数,f1为离心球与自毁锥面间的滚动摩擦系数,f2为击发体与击发体座内孔圆柱面间的滑动摩擦系数。
为表述方便,将式(4)简化,得动力学通用运动方程

(5)
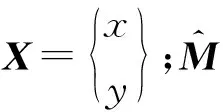
为外力列阵。
由离心球沿自毁锥面运动性质,可知在第一阶段有系统几何方程
(6)
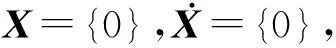
(7)
其中A、B满足如下关系式

(8)
令l1为离心球沿自毁锥面运动行程,当x=l1·sinα时,离心球沿自毁锥面运动的终了时间tk为:
(9)
则离心球沿自毁锥面运动过程结束的tk时刻对应速度为:
(10)
引信离心球自毁机构系统tk时刻对应的动能为:
(11)
2.2 离心球沿击发体座内孔圆柱面运动的动力学分析
离心球在击发体上的腔室内,击发体沿击发体座内孔圆柱面运动过程中,自毁簧所存储势能要克服击发体与击发体座产生的摩擦力Ff2、离心球与击发体座产生的摩擦力Fd从而消耗能量。再去除离心球在tk时刻的转动动能T转,其余部分则转变为离心球自毁机构系统戳击雷管的有效动能Td。由能量方程可知:
Td=Ttk+ΔE-(Ff2+Fd)·l2-T转,
(12)
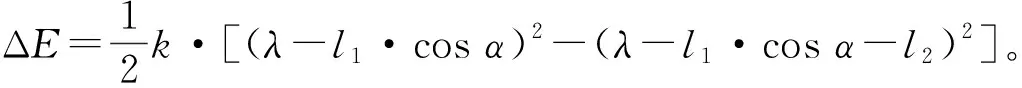
(13)
则有
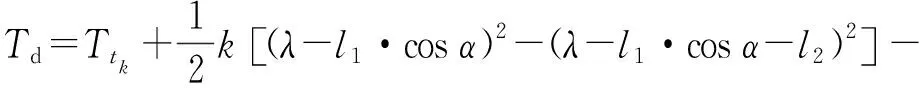
(14)
式(14)中,l2为引信离心球自毁机构系统沿击发体座内孔圆柱面运动行程,d为离心球与击发体座内孔圆柱面相切球心相对于弹丸旋转轴偏心距,f3为离心球与击发体座之间的滑动摩擦系数。
则由式(8)、式(9)、式(10)、式(11)、式(14)可得

2.3 理论分析验证
令α=0,得到引信离心球自毁机构系统沿自毁斜面运动tk时刻动能
如果α=0,则引信离心球自毁机构沿自毁斜面的运动过程就变为沿弹轴方向的竖直运动;又经验证可得α=0时求得的引信离心球自毁机构系统沿自毁斜面运动tk时刻动能Ttk恰好与假设引信离心球自毁机构系统作沿弹轴方向运动l1得到的末端动能相等,则理论分析结果可信。
令l1=0,得到引信离心球自毁机构系统自毁发火能量
(15)
由式(15)可知l1=0时,得到的引信离心球自毁机构系统自毁发火能量Td与单独针对系统沿击发体座内孔圆柱面运动过程求得的结果相符,且满足能量守恒方程的一般形式,因此验证了2.1节和2.2节理论分析的正确性。
3 离心球自毁机构作用仿真分析
3.1 仿真结构模型
为了进一步验证理论分析的正确性,运用ADAMS软件对引信离心球自毁机构运动特性进行仿真分析。以某35 mm口径榴弹发射器触发引信为研究背景,建立引信离心球自毁机构仿真模型如图3所示。该模型由击发体(含击针)、底座、离心球、自毁簧及上盖板(上盖板与击发体座固连)组成,且所处状态为临界自毁状态,该状态下的自毁簧是在发射时,先由后坐力压缩后再由离心球离心力撑在压缩状态下的。
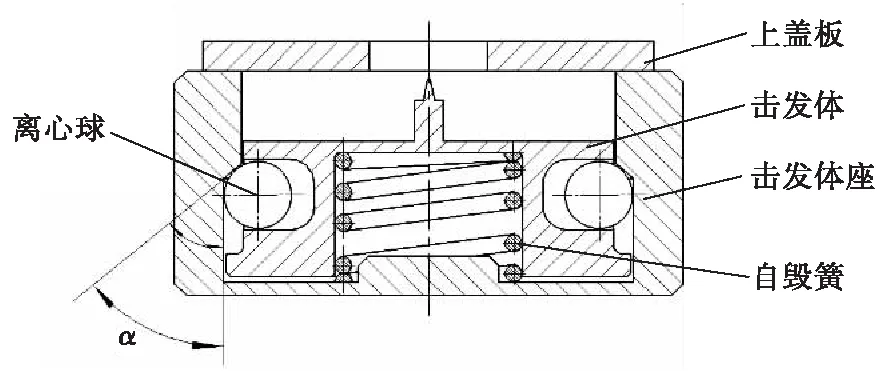
图3 机构仿真模型Fig.3 Simulation model of mechanism
图3所示的引信离心球自毁机构主要仿真参数如表1所列。其中摩擦系数的取值取决于常用金属材料之间的摩擦副。

表1 机构仿真参数Tab.1 Simulation parameters of mechanism
3.2 仿真分析
由表1仿真参数计算得到临界自毁角速度ωT=400.2 rad/s,为保证引信离心球自毁机构自毁时间恒定不变,则临界自毁角速度ωT=400.2 rad/s也应不变。引信离心球自毁机构自毁锥面锥角α、自毁簧刚度系数k、离心球离心半径r是影响自毁时间的主要因素。本文研究的是自毁锥面锥角对自毁发火能量和可靠性的影响,可以通过调节自毁簧刚度系数k、离心球离心半径r等其他影响因素来平衡自毁锥面锥角α的变化对自毁时间的影响,以保证自毁时间不变。
在自毁时间不变的前提下,本文分别通过调节自毁簧刚度系数k、离心球离心半径r两种因素来研究引信离心球自毁机构自毁锥面锥角变化对自毁发火能量的影响。
3.2.1调节自毁簧刚度系数仿真分析
在其他机构参数不变的条件下,仿真并计算引信离心球自毁机构自毁锥面锥角α分别为40°、41°、42°、43°、44°、45°、46°、47°、48°、49°、50°的运动情况,调节自毁簧刚度系数k的取值使得临界自毁角速度ωT=400.2 rad/s不变,得到其自毁簧刚度系数k及自毁发火能量,如表2所列。
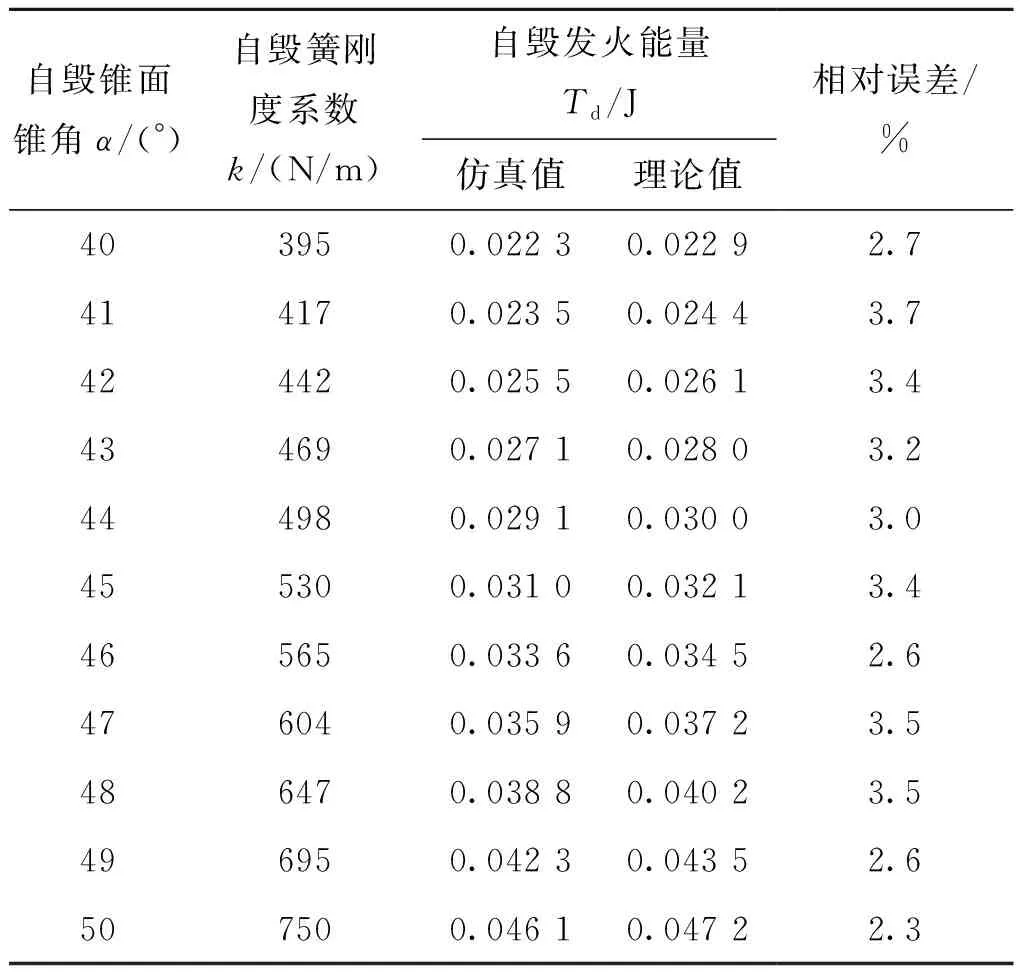
表2 不同自毁锥角对应自毁簧刚度系数及自毁发火能量Tab.2 Stiffness coefficient of destruct spring and destruct firing energy in different cone angle
将表2得到的自毁簧刚度系数k及自毁发火能量数值进行拟合,得到其变化曲线,结果如图4所示。
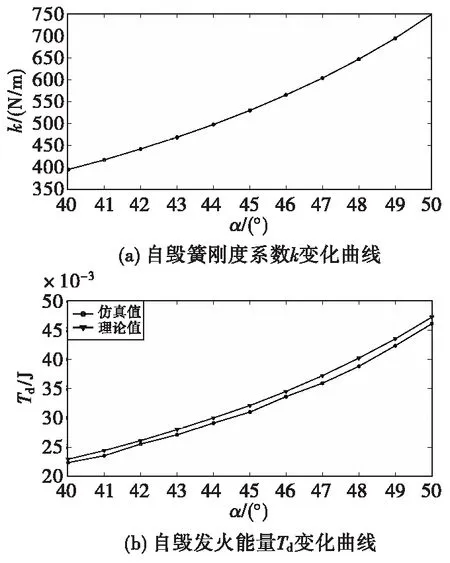
图4 不同自毁锥角对应自毁簧刚度系数及自毁 发火能量变化曲线Fig.4 The curve of stiffness coefficient of destruct spring and destruct firing energy in different cone angle
3.2.2调节离心球离心半径系数仿真分析
在其他机构参数不变的条件下,仿真并计算引信离心球自毁机构自毁锥面锥角α分别为40°、41°、42°、43°、44°、45°、46°、47°、48°、49°、50°的运动情况,调节离心球离心半径r的取值使得临界自毁角速度ωT=400.2 rad/s不变,得到其离心球离心半径r及自毁发火能量,如表3所列。
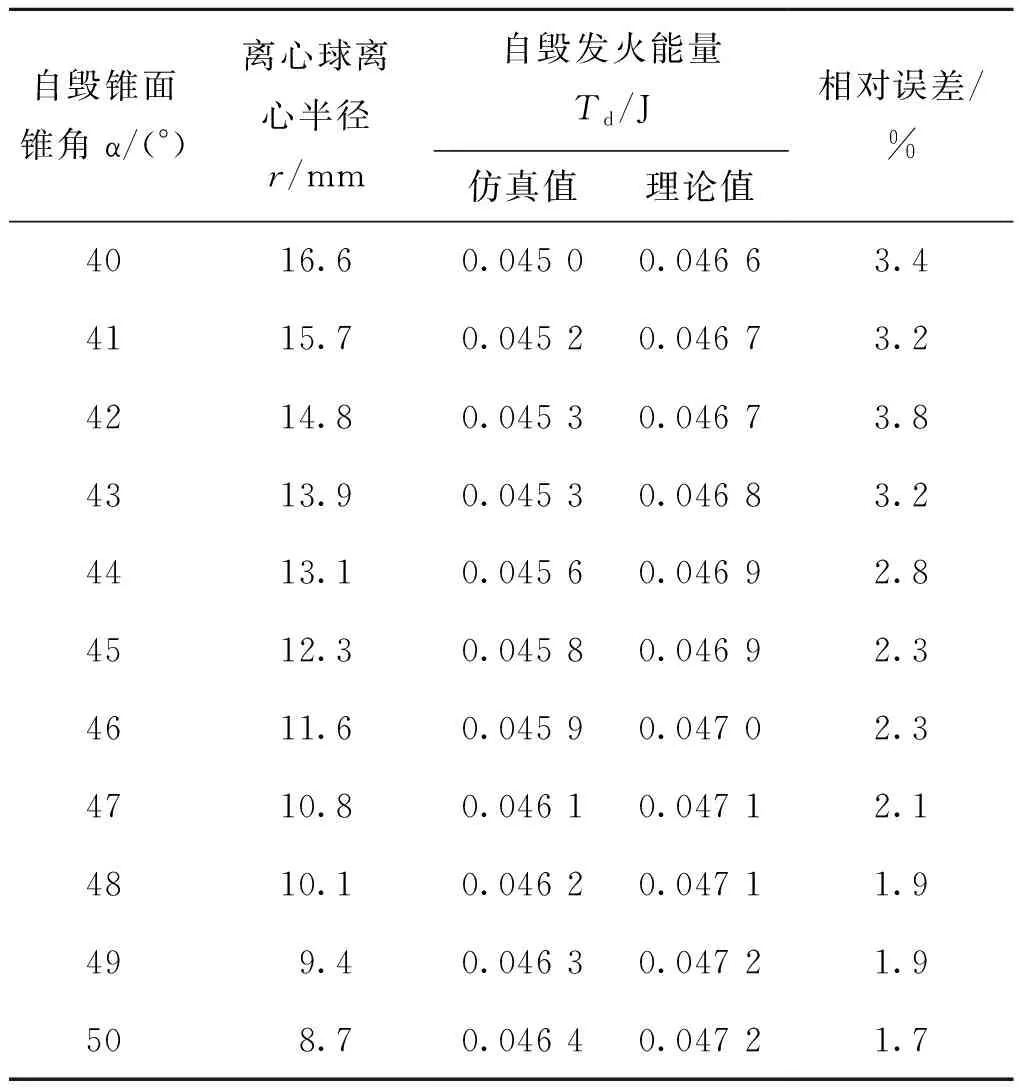
表3 不同自毁锥角对应离心球离心半径及自毁发火能量Tab.3 The centrifugal radius of centrifugal ball and destruct firing energy in different cone angle
将表3得到的离心球离心半径r及自毁发火能量数值进行拟合,得到其变化曲线,结果如图5所示。
本文研究的前提是保证自毁时间不变,在此情况下,单一考虑锥角影响,并无工程意义。在上述前提下得到自毁发火能量与锥角α的关系,如图4和图5所示。
3.3 仿真结果分析
由表2、表3、图4及图5可知:
1) 仿真得到的自毁发火能量数值与理论值变化趋势相符,且结果相近,误差不超过4%,验证了理论分析的正确性。
2) 为增大自毁能量且仍保持原方案的自毁时间不变,可以调整自毁簧刚度系数k及离心球离心半径r等影响自毁时间的关键因素以平衡自毁锥面锥角α变化对自毁时间产生的影响;在自毁时间恒定的前提下,自毁簧刚度系数k与自毁锥面锥角α呈正相关,而离心球离心半径r与自毁锥面锥角α呈负相关。
3) 在自毁时间恒定的条件下,无论是调整自毁簧刚度系数k还是调整离心球离心半径r以平衡自毁锥面锥角α变化对自毁时间产生的影响的方法,自毁发火能量都将随着自毁锥面锥角α的增大而增大;第一种方法相对于第二种方法来说,自毁锥面锥角α变化对自毁发火能量产生的影响更大,且自毁锥面锥角α每增加1°,第一种方法自毁发火能量增大约11%,第二种方法仅增大约0.13%。
4) 在自毁时间恒定的条件下,可以根据实际情况增加自毁锥面锥角α以增大自毁发火能量,然而自毁锥面锥角α却不能无限制的增大,必须要满足引信离心球自毁机构自毁锥面锥角α不自锁的条件式,即α≤90°-[arctan(f3)+arctan(f4)]。
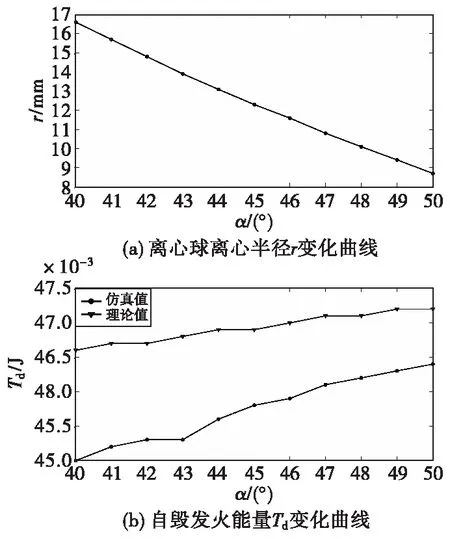
图5 不同自毁锥角对应离心球离心半径及 自毁发火能量变化曲线Fig.5 The curve of centrifugal radius of centrifugal ball and destruct firing energy in different cone angle
小口径引信在高发射过载、高转速下的瞬态现象目前难以观测到,故本文所得理论研究结果难以进行直接的试验验证。但按此分析得到的设计原则已在35 mm口径榴弹发射器新型引信型号研发过程中采用,并已得到了规律正确性验证。
4 结论
本文提出引信离心球自毁机构作用动力学建模与仿真方法。该方法指出为确保自毁可靠性,可以通过锥角调整增大自毁发火能量,但因此而改变了自毁临界角速度,自毁时间发生了变化,为平衡这种变化,可通过调整自毁簧刚度系数以及离心球离心半径来实现。通过理论分析表明,自毁锥面在80°~100°范围内变化时,其中自毁锥面锥角每增加1°,对应调整自毁簧刚度系数自毁发火能量增大约11%,而对应调整离心球离心半径自毁发火能量增大约0.13%。
