基于微元法的侵彻体弹头摩擦升温计算方法
2022-05-13范锦彪耿宇飞
邵 伟,范锦彪,耿宇飞,王 玮
(中北大学仪器科学与动态测试教育部重点实验室,山西 太原 030051)
0 引言
侵彻过程中弹靶间发生的高速滑动摩擦主要集中在弹头处,其中摩擦力做功的90%以上将转化为热能,导致弹头表面温度剧变[1-3]。
该部分摩擦温度需在瞬态条件下获取,难度较大。文献[4]先将弹头锥面近似分解为无数个的等边三角形,通过弹体侵彻过程中摩擦力和法向力,计算出每个三角形上的热流强度,再乘以热流持续时间,得到弹头单位面积上的摩擦升温值;文献[5]先在弹体侵彻中承受介质阻抗外力公式的基础上分析得到弹体所受摩擦力的表达式,再分析了摩擦力与温度的转化公式,将摩擦力表达式带入到转化公式中,得到弹头处摩擦升温值;文献[6]对侵彻过程中弹体所受的等效摩擦应力、滑动率、摩擦功转热系数和摩擦功耗散功率四项求积得到摩擦升温值。
由上述介绍可知,这些方法都是将弹体侵彻混凝土靶摩擦升温瞬态过程简化为稳态过程,弹头处受到摩擦力、法向力和侵彻速度等按均值处理,其分析过程不严密必然导致计算精度较低。本文针对该问题,根据Forrestal侵彻阻力分析法和摩擦热力学,提出基于微元法的侵彻体弹头摩擦升温计算方法。
1 Forrestal侵彻阻力分析法及摩擦 热力学
1.1 Forrestal侵彻阻力分析法
文献[7—9]基于对侵彻体侵彻土壤类介质的摩擦阻力分析,提出侵彻混凝土力学方程。当侵彻目标靶为混凝土时,侵彻体侵彻通道先后为开坑区和贯穿洞区。Forrestal认为开坑过程发生在4R(R为侵彻体半径)深度内,侵彻阻力随侵彻深度增大而线性增大,该区域的力学变化满足胡克定律[10-11]。当深度大于4R之后,侵彻阻力与深度的关系可采用空腔膨胀理论描述,Forrestal提出整个过程的轴向阻力计算公式为:
(1)
式(1)中,C为侵彻阻力系数,h为侵彻深度,B为动阻力项系数,B=1,fc为材料的单向无侧限抗压强度,N为侵彻体头部形状因子,ρ为混凝土密度,v为侵彻体速度,S为侵彻过程中高温高压以及高应变率效应对靶体强度的影响。
文献[12]提出当16.5 MPa≤fc≤176 MPa时,S与fc的转化关系:
(2)
侵彻阻力系数C和头部因子N的表达式为:
(3)
N=(8Ψ-1)/(24Ψ2),
(4)
式(3)、式(4)中,m为侵彻体质量,v0侵彻体初速度,v1为开坑结束时的速度,Ψ为曲径比。
当侵入深度为4R开坑阶段结束,撞击过程也随之结束。根据连续性,由式(1)可得,此时的侵彻体速度为:
(5)
联立式(3)和式(5),可得侵彻阻力系数C表达式为:
(6)
1.2 摩擦热力学理论
热力学是为研究热现象和力现象两者之间的关系发展起来的宏观唯向学理论。摩擦过程热量场的变化特点是:具有很大的空间和时间梯度,使热应力以热冲击的形式表现出来[1],将动能转化为热能(假设能量无其他形式的损耗)。
摩擦生热是相互摩擦的物体表面分子相互碰撞生热的结果:假定一个物体(混凝土靶)静止,另一物体(侵彻体)相对该物体运动;在此过程中,静止物体中的分子被撞击,获得了运动物体中分子的部分或全部定向动能,使接触面分子热运动动能增大,相互碰撞频率增多;从而导致相互摩擦的物体表面在宏观上表现为内能增大,温度升高。一般摩擦产生的热量用式(7)计算。
Q=Ff·s,
(7)
式(7)中,Ff为两物体接触面的滑动摩擦力,s为两物体的相对位移,计算公式为:
s=v·t,
(8)
式(8)中,v为物体运动的速度,t为物体运动的时间。
2 基于微元法的弹头摩擦温度计算
2.1 侵彻体头部受力分析
由1.1节可知,本文分析弹头完全撞击侵入目标靶时的摩擦阻力属于开坑阶段。由式(1)可计算得到开坑阶段任何深度侵彻体的阻力大小,再对阻力受力分析,得到弹头表面所受的摩擦力大小。受力分析如图1所示。
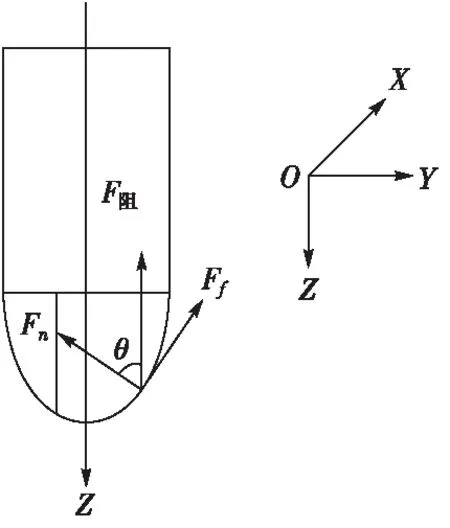
图1 受力分析图Fig.1 Stress analysis diagram
图1受力分析代表某个时刻摩擦力的大小和方向,图中F阻为轴向阻力,Fn为法向力,Ff为切向力,即摩擦力。分析可知摩擦力大小取决于该时刻弹头侵入混凝土靶深度所对应的阻力大小和弹头的切线方向的变化情况。当弹头全部侵入混凝土靶板后θ=90°,摩擦力方向不再变化。
由图1可知,侵彻体撞击侵入靶板时,弹头所受摩擦力为:
Ff=F·sinθ。
(9)
联立式(3)、式(7)和式(9),可得摩擦力表达式:
(10)
由式(1)和牛顿第二定律式(11),可得开坑过程中撞击深度、速度和时间的关系,如式(12)和式(13)所示:
(11)
(12)
(13)
式中h为侵彻体撞击侵入靶板的深度,vt为某一时刻速度,t为时间,w为无量纲常数,表达式为:
(14)
联立式(10)和式(12),可得到摩擦力的表达式如式(15)所示。可知弹头处的摩擦力是关于时间t和夹角θ的函数。
(15)
2.2 摩擦热量计算
微元法是一种从部分到整体的思维方法,该法可使一些复杂的物理过程简化成我们熟悉的规律加以解决。基于微元法的摩擦温度计算思路是将弹头表面分解为无数个小长方条,先计算出每个小长方条在整个撞击过程中的热量数值,设为Q0,再对整个弹头表面的Q0积分,即可得到整个弹头表面的总热量Q,转化关系式为:
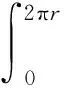
(16)
式(16)中,r为弹头侵入靶板的切面圆半径。
现将总热量的计算转换为小长方条的热量的计算(设摩擦力做功全部转化为热量),式(7)用于计算分析匀速、匀摩擦力条件下的摩擦热量,而在侵彻过程中速度和摩擦力均处在动态变化的过程中,式(7)结合微元法可得
(17)
式(17)中,Ff为滑动摩擦力,v为速度,t为时间。
由式(12)和式(13)可知,撞击速度和深度是关于时间t和夹角θ的函数,所以对时间和夹角在对应的区间内积分即可。联立式(12)、(13)、(14)和式(17),积分得出Q0的计算公式。分析可知,时间的区间为(0,t),夹角的区间为(0,π/2),可得:
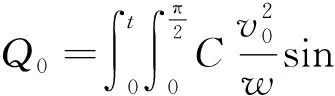
(18)
联立式(16)和式(18),可得弹头完全撞击侵入总热量Q的表达式:
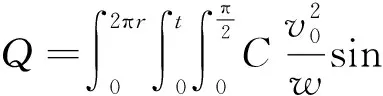
(19)
2.3 热量与温度的转换
文献[13]提出高速摩擦条件下瞬态热量与温度的转换方法,对高速移动源热量被供应到一个固定区域并存在稳态条件时,热流可以看作流经热阻。在本文的情况中,弹头完全侵入混凝土靶时,可将弹靶接触面的热量看作供应在固定区域。通过式(19)计算出(0,t)内累积的热量值Q,对t时刻Q可视为一个稳态值。满足瞬态热量与温度的转换条件。设弹头在整个过程的温度变化量为T,转换公式为:
(20)
式(20)中,Q为侵彻过程中弹靶接触面摩擦产生的总热量,r为撞击时弹头完全侵入混凝土靶的接触半径,λ为侵彻体导热系数。
联立式(19)和式(20),可得侵彻体侵彻混凝土靶摩擦升温计算式:
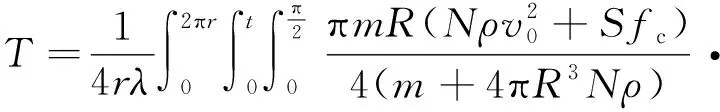
(21)
化简得
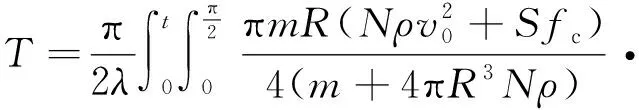
(24)
3 算例分析
3.1 理论计算
设侵彻体半径和长度分别为1.3 cm和3.9 cm,弹头形状为半球型,其他参数如表1所示。混凝土靶参数如表2所示。
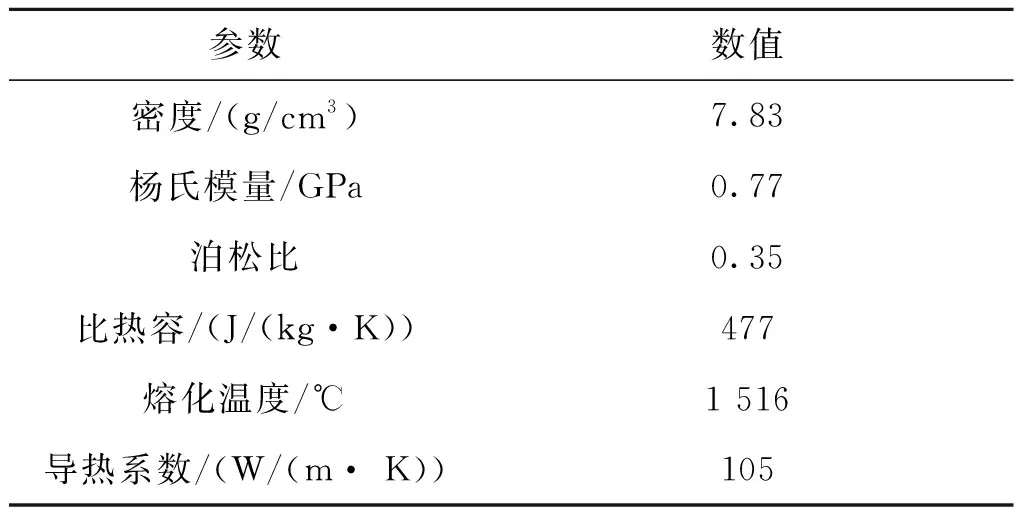
表1 侵彻体参数Tab.1 Parameters of penetration body
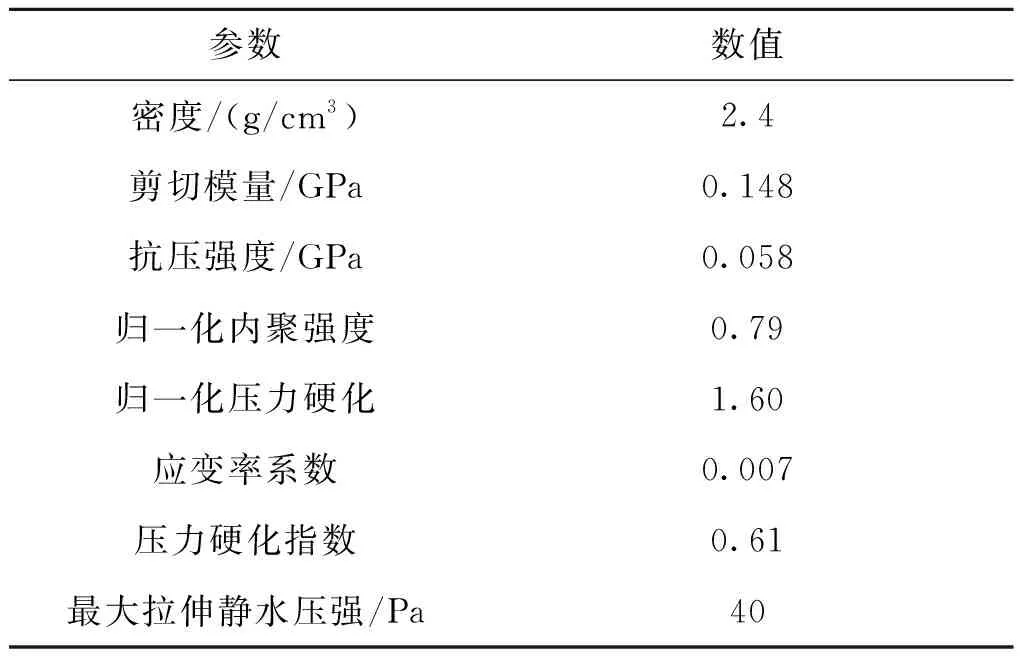
表2 混凝土靶参数Tab.2 Concrete target parameter
设侵彻体撞击初速度v0=800 m/s,将表1和表2中的相关参数代入式(22),可得摩擦温度变化趋势图,如图2所示。初始温度为0 ℃弹头完全侵入混凝土靶时摩擦升温值对应图中最高点温度,此值为1 619 ℃。
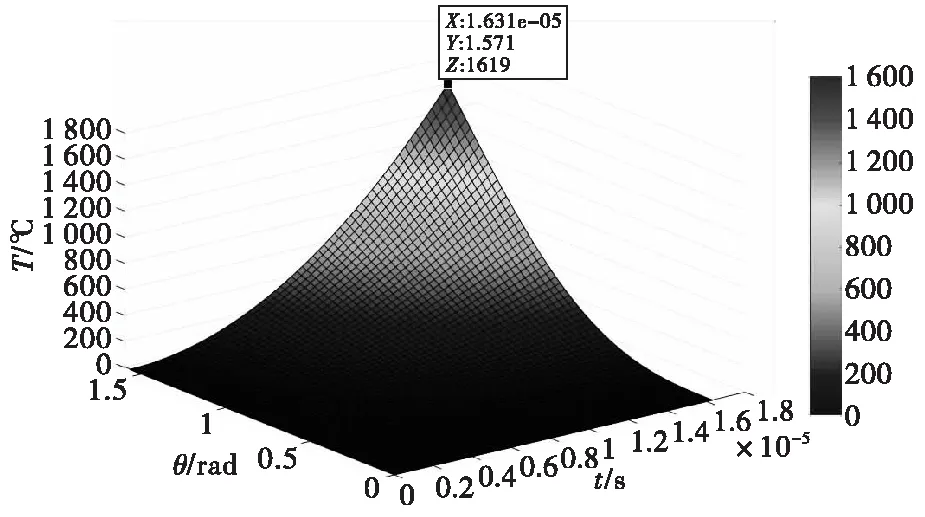
图2 温度变化趋势图Fig.2 Temperature change trend
由图2可知侵彻体撞击侵入混凝土靶时,弹头处摩擦温度T是关于时间t和夹角θ的时空分布函数。撞击侵入伊始,弹靶接触面积小,升温速率较缓。随着弹头不断侵入,接触面积变大,升温速率随之加快。
分别计算初速度v0为800、600、400和200 m/s下的升温值可得表3。

表3 不同初速度下的升温值Tab.3 Heating values at different initial speeds
3.2 仿真计算
有限元软件ANSYS/LS-DYNA求解非线性动力学等问题功能强大。针对各种情况下的高速碰撞模拟分析、侵彻过程、爆炸过程和坑状模拟分析等高度非线性瞬态动力学问题优势巨大。本文使用该软件完成仿真模拟实验,仿真类型为热-固耦合分析,单位制采用cm-g-μs。在建模中弹靶接触的核心区域划分为更加密集的网格。在靶板底部施加约束,模拟固定的靶板。由于模型结构和载荷上的对称性,采用1/4建模的方式。时间步长由式(23)确定[5],减少无关因素对仿真的影响,有限元模型如图3所示。
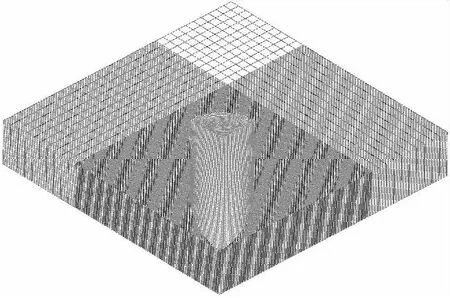
图3 弹靶有限元模型Fig.3 Finite element model of projectile target
(23)
式(23)中,L为划分网格单元的特征长度,C1为材料在空气中传播时所具有的声速。
本文针对高速摩擦热,不考虑塑型变形热且侵彻体撞击混凝土靶速度低于800 m/s时,可视为刚体不考虑型变和质量磨损[12],侵彻体材料定义为Rigid型,在热固耦合分析中,该型材料不反映升温值,需通过定义“Contact”和“Eroding_suface_to_suface”等关键字,使其具有温升效应。侵彻体参数如表1所示。混凝土靶定义为HJC型,该模型考虑了应变率、平均正应力以及材料破坏与屈服应力的关系,描述侵彻混凝土具有较高的准确度[14],混凝土靶参数如表2所示。
本文基于Forrestal半经验侵彻阻力分析方法,提出侵彻时弹头处的摩擦升温计算方法。在侵彻阻力分析式(1)中未包含显式的摩擦系数项,其原因是该模型中参量S是通过大量的侵彻实验确定的,摩擦系数隐含其中[15]。而在弹靶有限元仿真模拟中,摩擦系数是一个极为重要的参数,因此需确定一个参考性高的摩擦系数值。
在理论阻力模型中,Forrestal推导的混凝土阻力模型未考虑摩擦系数[16],结果导致理论值比实验值偏大,随后对上述方法进行了修正,提出侵彻体无论侵彻的目标是地质类靶还是金属靶[17],摩擦系数取0.1时,理论值与实验值吻合的更好,基于此结论摩擦系数取0.1。
侵彻过程中存在多种干扰因素,因此对整个仿真过程需做如下假设[3]:1) 摩擦产生的热量无损失,全部转换为侵彻体的升温值;2) 侵彻体材料各物性参数恒定,不随温度的变化而变化;3) 选择弹头某一网格面,代表弹头表面温度变化趋势。
在ANSYS/LS-DYNA材料参数定义中输入表1和表2 参数,并完成接触类型和侵蚀面类型等关键字的定义,完成前处理。仿真过程如图4所示,初始温度为20 ℃,撞击初速度为800 m/s,侵入时间5.2 μs。由温度云图可知此时侵彻体最高温度为194.2 ℃。

图4 仿真过程图Fig.4 Temperature simulation cloud
本文所用弹靶材料参数与文献[18]中的参数相同。相同速度下得到的仿真温度如表4所示。
由表4可知,本文仿真结果与文献[18]中的结果相差较小,二者存在差距主要原因是弹体几何形状的差别,在一定程度上验证了本文模型的准确性。同时本文仿真得到的侵彻体头部撞击侵入靶板的时间与Forrestal侵彻阻力分析公式(式(12))计算得到时间几乎一致,结果对比如表5所示。

表4 温度对比Tab.4 Temperature comparison
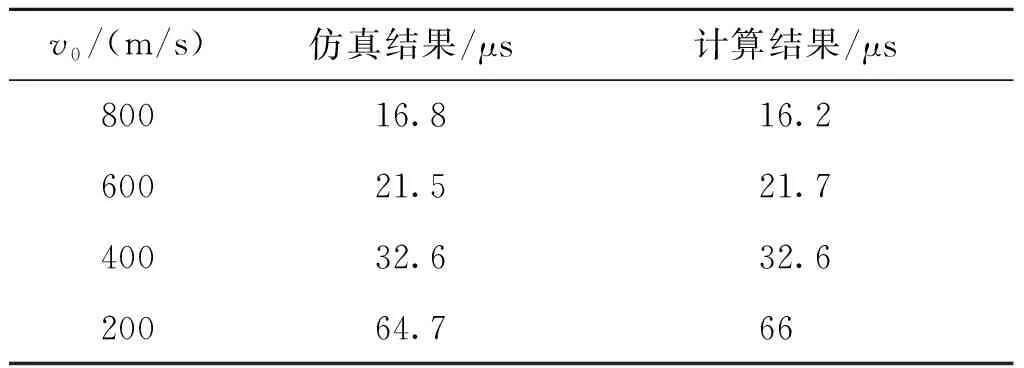
表5 侵彻时间对比Tab.5 Comparison of penetration time
表5的对比结果,从另一方面也验证了本文模型的准确性。
3.3 理论与仿真计算结果分析
由式(22)可知侵彻摩擦温度T是关于时间t夹角θ的函数,而LS-DYNA仿真软件中只能反映出温度随时间的变化关系。为了便于比较,先完成式(22)中变量θ的积分计算,将温度只表示为时间的函数:
(24)
设初始温度为20 ℃,侵彻体初速度分别为800、600、400和200 m/s,将表1和表2中的参数带入式(24)中,理论计算值与LS-DYNA仿真升温趋势对比如图5—图8所示。
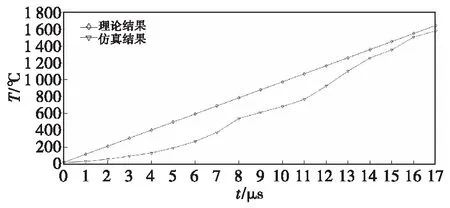
图5 初速800 m/s撞击温度变化趋势Fig.5 Variation trend of impact temperature with initial velocity of 800 m/s
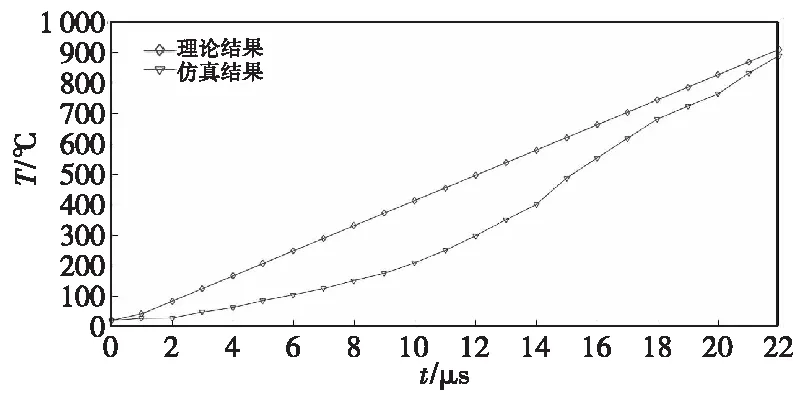
图6 初速600 m/s撞击温度变化趋势Fig.6 Variation trend of impact temperature with initial velocity of 600 m/s
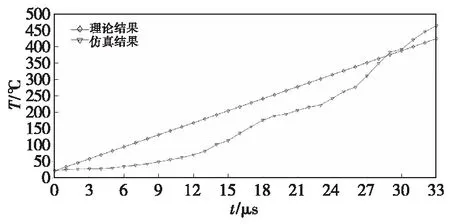
图7 初速400 m/s撞击温度变化趋势Fig.7 Variation trend of impact temperature with initial velocity of 400 m/s
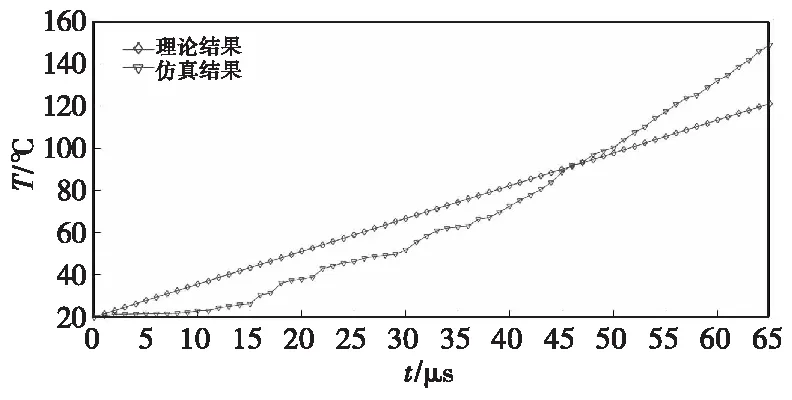
图8 初速200 m/s撞击温度变化趋势Fig.8 Variation trend of impact temperature with initial velocity of 200 m/s
由图5—图8可得出,当侵彻体头部完全撞击侵入靶板时,基于微元法的温度计算结果与LS-DYNA仿真结果吻合较好。图5—图8仿真与理论的最高温度值对比如表6所示。
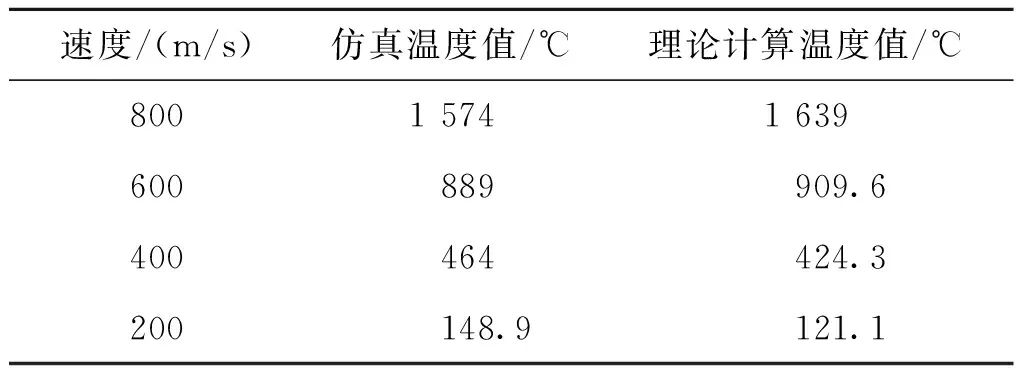
表6 系列初速下温度值仿真与理论计算结果对比Tab.6 Comparison of series speed simulation and theoretical calculation results
侵彻体以800、600和200 m/s的初速度撞击,以仿真结果为参考,相对误差仅为4.1%、2.2%和1.8%;而以400 m/s的速度撞击时,二者吻合性较差,相对误差为8%。侵彻体撞击初速度为400和200 m/s时,仿真最终的升温值大于理论计算值。从系列图中可以看出侵彻体撞击侵入的初始阶段,初速度越低,理论计算结果和仿真结果吻合得更好。
理论和实验曲线图存在差异的原因可能是理论公式计算中将弹靶接触面考虑为光滑面,而建立的弹靶有限元模型是由若干表面不连续的微小网格组成。初始网格数量少,理论计算结果与仿真结果相差较大。随着弹头的不断侵入,网格数量增多,二者结果吻合性也会随之增高。
侵彻体撞击初速度为800 m/s时,弹头处摩擦升温值超过侵彻体材料的熔点,所以可将800 m/s的撞击初速度视为侵彻体材料熔化的临界速度。侵彻体材料的熔化不仅与温度的高低有关,而且与该温度持续的时间有关,因此侵彻体材料是否会熔化还有待于进一步论证。
4 结论
本文提出基于微元法的侵彻体弹头摩擦升温计算方法。该方法在微元法的基础上构建了侵彻体轴向阻力-摩擦力-热量-温度的函数式,通过设定的侵彻体初速度、靶体密度、导热系数等物理参数获得侵彻体头部的温升曲线。理论计算结果表明,侵彻体分别以800、600、400和200 m/s的速度侵彻目标时升温理论计算结果与以仿真结果误差仅为4.1%、8%、2.2%和1.8%,理论计算结果和仿真结果吻合性较好,更适合用于侵彻体弹头摩擦升温理论计算。
本文不足之处:仿真中以选择的小网格表示整个弹头面的升温变化趋势,存在一定得局限性。由于目前无法通过实测试验得到侵彻体头部摩擦升温值,所以本文只针对静态条件下的弹靶物理参数,计算获得理论上的摩擦升温值。而动态条件下的计算结果,还有待于进一步研究。
仿真结果虽与所引文献差异较小,但在仿真中仍存在多种影响因素,如弹靶初始网格大小、时间步长等都可能会对仿真结果产生影响,可建立多组模型进一步论证。
