基于径向基函数和自组织映射的导弹控制系统健康状态评估
2022-05-13刘月刘铁林姜相争韩月明
刘月, 刘铁林, 姜相争, 韩月明
(1.陆军工程大学石家庄校区 装备指挥与管理系, 河北 石家庄 050000; 2.93786部队, 河北 张家口 075000)
0 引言
随着军队信息化、智能化建设的不断发展与推进,导弹武器系统功能不断扩展,规模日益扩大,但同时也由于系统复杂性、关联性、任务环境多样性等导致一系列新的故障问题,传统导弹故障检测和维修保障方法越来越无法适应现代战争快节奏、高效率的装备精准保障需求。因此有学者提出视情维修(CBM)的理念,用以实现武器装备故障及健康状态的精确认知,降低维修保障成本,提高导弹的安全性和可用性。
控制系统是导弹能够完成任务的关键,对导弹的控制系统进行健康状态评估,有助于提高导弹装备全寿命可用度,优化装备维修决策与战场综合保障,做到早诊断、早发现、早维修、适时微损微修。传统导弹武器装备的健康状态评估方法通常为专家评分法,即专家根据测试参数的结果,按照经验进行任务系统选择。这一类方法严重依赖设计人员与产品专家的经验与水平,效率低,准确度差。对于大规模的测试数据结果,数据可靠度低,有较高的偶然性,不利于对对象产品进行健康状态评估。
目前常用基于数据驱动的健康状态评估算法可以分为基于概率的评估方法和基于神经网络的评估方法。基于概率的评估方法主要包括隐马尔可夫模型(HMM)和高斯混合模型(GMM)。HMM模型通过一个马尔可夫链来描述模型中各种状态之间的转移过程,而马尔可夫链中观测量与状态量之间可以通过随机过程描述二者的对应关系,通过构建不同健康状态的HMM模型,可以实现健康状态的识别。GMM模型是指多个高斯分布函数的线性组合,通常用于解决同一集合下数据包含多个不同分布的情况。通过构建不同健康状态下的概率密度函数,可以计算不同概率密度函数之间的距离,实现健康状态的度量。然而,HMM模型的训练需要大量的先验概率,GMM模型必须假设数据基本服从高斯分布,目前导弹武器装备的监测数据却很难满足这些要求。基于神经网络的评估方法包括径向基函数(RBF)网络以及自组织映射(SOM)网络。RBF网络是一种典型的三层前馈神经网络,能够通过RBF实现不同健康状态数据的聚类或分类。一方面,目前基于RBF的故障诊断模型主要是以系统的输出数据为输入,系统状态为输出构建RBF网络,然而该方法并不适用于具有反馈信号的控制系统故障诊断;另一方面,目前基于RBF的故障诊断模型仅针对单一工作状态和测试输入信号条件下的故障诊断问题,即存在唯一的故障判据或故障判别阈值,无法解决具有不同故障判别阈值的多工作状态和输入信号条件故障诊断。SOM网络是一种无监督学习模型,通过神经元之间的竞争学习过程实现不同健康状态数据的聚类或分类。目前基于SOM网络的健康状态评估模型仅利用健康状态的监测数据构建SOM网络,通过衡量当前状态与健康状态的偏离程度实现健康度的计算,然而该方法并未考虑到当前状态与故障状态偏离程度的影响。
为实现导弹控制系统准确、高效、客观的健康状态评估,本文开展基于数据驱动的导弹控制系统健康状态评估算法研究。考虑到导弹控制系统在实际使用和测试过程中的反馈特性以及具有不同的工作状态和输入信号要求,本文一方面考虑控制系统的输入输出信号,利用RBF网络建立控制系统的故障观测器并生成输出信号残差,另一方面构建新的RBF网络,用于计算不同的工作状态和输入信号条件下的自适应判别阈值。同时考虑当前状态、健康状态和故障状态三者之间的偏离关系,建立基于健康状态和故障状态监测数据的SOM网络,用于未发生故障的导弹控制系统的健康状态评估。
1 整体思路
导弹控制系统健康状态评估的整体思路和流程如图1所示,共包含两个部分,基于RBF网络的自适应故障观测器以及基于SOM网络的健康状态评估模型。
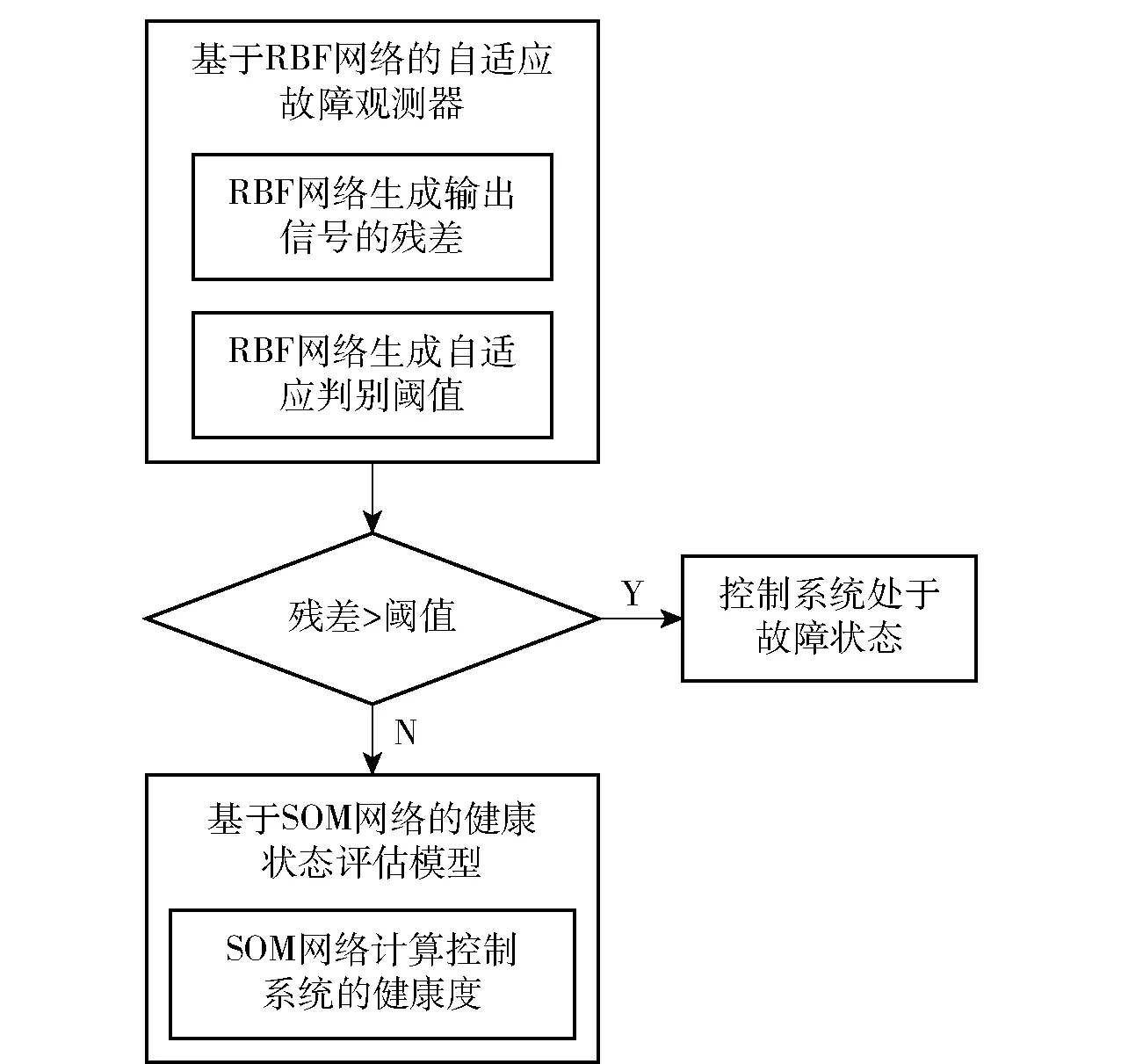
图1 整体思路和流程Fig.1 Overall idea and process
在基于RBF网络的自适应故障观测器中,首先利用RBF网络模拟控制系统的观测器,计算输出信号并评估输出信号的残差,然后利用RBF网络生成不同工作状态、不同输入信号下残差的自适应判别阈值,并判定导弹控制系统是否发生故障。若发生故障,则此时导弹控制系统的健康度为0,需要进行进一步检查和维修;若判定导弹控制系统未发生故障,则对导弹的健康状态进行评估。在基于SOM网络的健康状态评估模型中,利用SOM网络对残差数据进行聚类分析,并对导弹控制系统的健康状态进行评估。
2 基于RBF网络的自适应故障观测器
2.1 RBF网络
RBF网络是一种常用的三层前馈神经网络,包括输入层、隐含层和输出层。其中:隐含层的作用是把向量从低维度映射到高维度,使得低维度线性不可分的情况到高维度就可以线性可分;输入层和隐含层间由高斯函数映射构成,可以将输入矢量直接映射到隐空间,因此从输入空间到隐含层空间的变换是非线性的;输出层与隐含层则由简单的线性函数映射构成,即网络的输出是隐单元输出的线性加权和,因此从隐含层空间到输出层空间变换是线性的。由于网络由输入到输出的映射是非线性的,而网络输出对可调权重却又是线性的,网络的权重就可由线性方程组直接解出,从而可大大加快学习速度并避免局部极小问题。
RBF是一个取值仅依赖于离原点距离的实值函数,即()=(‖‖)(为输入节点向量),或者还可以是到任意一点的距离,也就是(,)=(‖-‖)(为中心向量)。通常使用高斯函数作为RBF:
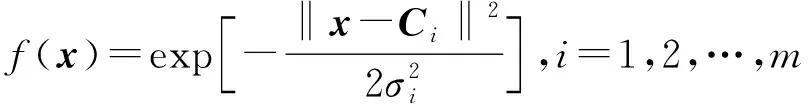
(1)
式中:为第个RBF的中心;为第个RBF的方差,它决定了该基函数围绕中心点的宽度;为RBF的个数。
在传统反向传播(BP)神经网络中,网络的求解参数包括输入层到隐含层的连接权值以及隐含层到输出层的连接权值;而在RBF网络中,由于输入层到隐含层的线性连接被RBF所代替,RBF网络的求解参数有3个:RBF的中心、方差以及隐含层到输出层的连接权值。
1)RBF的中心。通过K-means聚类方法确定聚类中心,并将第类样本的聚类中心作为第个RBF的中心。
2)RBF的方差。RBF标准差的确定原则是使所有RBF单元的接受域之和覆盖整个训练样本空间,因此可以令相应的标准差等于其与属于该类训练样本之间的平均距离,即
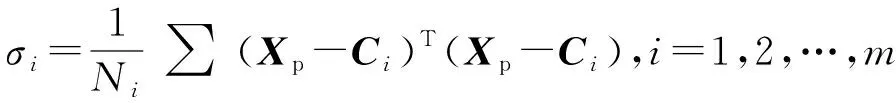
(2)
式中:为属于第类样本的样本数;表示属于以为聚类中心的第类样本。
3)隐含层到输出层的连接权值。权值的调整采用梯度下降法,其迭代公式为
(+1)=()+(-)()
(3)
式中:()为隐藏层到输出层的连接权重矩阵;为学习速率;为网络的期望输出;为网络的实际输出;()为隐含层输出。
2.2 自适应故障观测器
在控制系统中,观测器是一种可以根据系统输入和输出变量实测值来实现状态变量估值的动态系统,因此经常构建故障观测器以对控制系统进行故障诊断。故障诊断基本原理是利用控制系统的真实输出与观测器的估计输出生成残差,并与相应的故障判别阈值进行比较。
然而这种方法主要适用于线性控制系统,且要求没有未知参数。针对现阶段交联关系复杂的控制系统以及非线性故障特征,传统基于数学模型的故障观测器已不再适用。考虑到RBF网络具有强大的非线性拟合能力,且仅需要控制系统的输入和输出信息,不需要考虑大量的系统参数,因此采用RBF网络作为非线性函数估计器对控制系统进行重构,构建逼近控制系统真实情况的故障观测器,以解决复杂控制系统的故障检测问题。
将传统观测器与RBF网络相结合,建立基于RBF网络的自适应故障观测器,其结构原理图如图2所示。
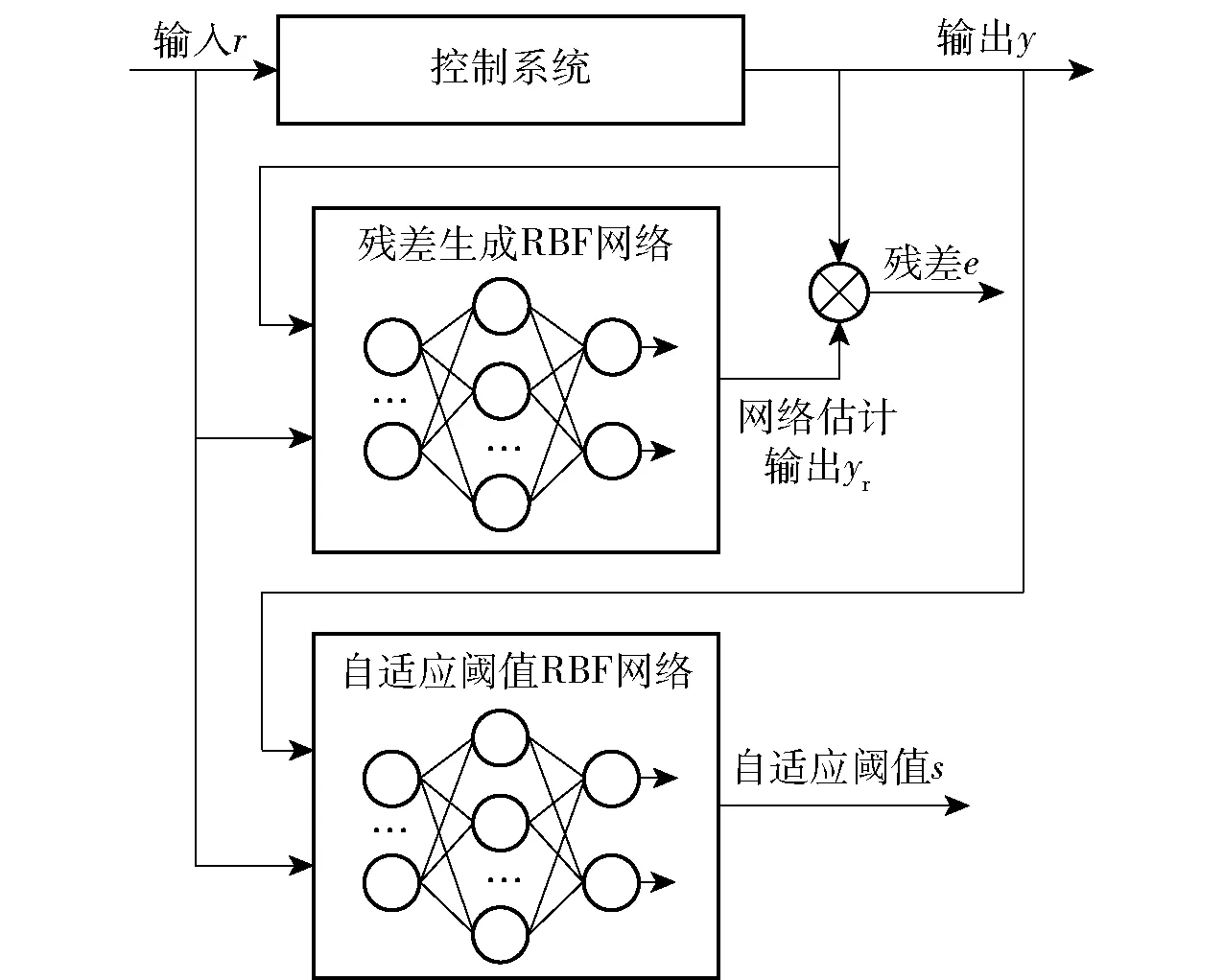
图2 基于RBF网络的自适应故障观测器Fig.2 Adaptive fault observer based on RBF network
该故障观测器包括两个RBF网络:第1个是残差生成RBF网络,RBF网络以控制系统的输入和输出信号为网络输入,以控制系统的估计输出信号为网络输出,用于计算控制系统的实际输出信号与估计输出信号的残差;第2个是自适应阈值RBF网络,RBF网络以控制系统输入和输出信号为网络输入,以不同工作状态、不同输入信号下故障判别阈值为网络的输出,用以生成随系统状态或者输入指令变化的判别阈值,排除因非故障原因引起的误差。
利用基于RBF网络的自适应故障观测器进行故障检测的基本原理,依然是基于残差与故障判别阈值的比较,当计算残差超过此时判别阈值时控制系统发生故障。具体实施步骤如下:
1)选取控制系统在所有工作状态以及所有输入信号下的正常输入和输出信号。
2)设置RBF网络结构参数。
3)分别建立不同工作状态下的残差生成RBF网络。对不同工作状态下的残差生成RBF网络进行训练,训练数据输入为各工作状态下正常的输入和输出信号,训练数据输出为各工作状态下的正常残差数据。
4)建立统一自适应阈值RBF网络。对自适应阈值RBF网络进行训练,训练数据的输入为控制系统正常的输入和输出信号,训练数据的输出为各工作状态以及各输入信号下的故障阈值。
5)对于待评估数据,首先利用构建完成统一的自适应阈值RBF网络,输入待评估数据对应的输入信号以及对应工作状态下的正常输出信号,生成故障判别阈值;其次利用对应工作状态下构建完成的残差生成RBF网络,输入待评估数据对应的输入和输出信号,生成对应的残差。若残差超过自适应阈值,则判定控制系统故障。
3 基于SOM网络的健康状态评估模型
3.1 SOM网络
SOM网络是一种自组织竞争人工神经网络,它以无监督竞争学习方式进行网络训练,具有自组织功能。SOM网络结构只有输入层和竞争层2层,输入层神经元的数量由输入向量的维度决定;常见的竞争层有一维结构和二维结构,其神经元数量决定了最终模型的粒度与规模。SOM网络的基本思想是网络竞争层中的各神经元通过竞争来获取对输入模式的响应机会,最后剩一个神经元成为竞争的胜利者,并对那些与获胜神经元有关的各连接全朝着更有利于它竞争的方向调整。
SOM网络的学习过程有别于BP网络,不需要提前给定任何目标输出,可以不必知道输入矢量的类型关系,因此该网络常用于数据聚类或分类。当输入矢量输入到网络后,网络利用随机选取的权值进行计算,并找到优胜神经元;然后调整权值,用收缩邻域和学习因子(随时间而收缩)的办法,最终使权值形成一组能映射输入的数据,当网络自组织形成时训练就结束。具体训练过程如下:
初始化,对竞争层各神经元权重赋随机数初值并进行归一化,建立初始优胜邻域和学习率。
对输入数据进行归一化处理。
遍历竞争层中每一个神经元,计算输入数据与每一个神经元之间的相似度,即与该神经元的连接权重向量的相似度,并选取距离最小的神经元作为优胜神经元。
确定优胜邻域包含的神经元。优胜邻域为训练时间的函数,一般初始邻域较大,而后邻域随训练时间逐渐收缩,常用的收缩邻域包括摩尔邻域和六边形网格领域。
计算优胜邻域内神经元各自的学习率并更新它们的权重。基本思想是:越靠近优胜节点,学习率越大;越远离优胜节点,学习率越小,即
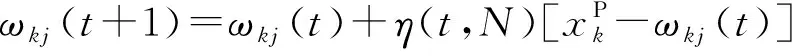
(4)
(,)=()e-
(5)
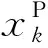
完成一轮迭代,返回步骤2,直到学习率降为0或满足设定的迭代次数。
在训练好的SOM网络中,由于竞争层的每一个神经元代表一个聚类类别,且为该类的聚类中心,输入层的每一组训练数据将最终映射到竞争层的唯一神经元中,并以one-hot编码的形式作为输出,即每一组训练数据对应的优胜神经元输出为1,其余神经元输出为0。而针对待分类的数据,计算其与竞争层每一个神经元的相似度,选择相似度最大或距离最小的神经元作为其分类结果。
3.2 健康状态评估模型
控制系统因结构组成和交联关系非常复杂,而且状态监测数据及其特征参数与系统健康度的函数关系不明显,难以建立准确的模型对其状态进行有效描述。而SOM神经网络以其高度的自组织、自学习特性,能够直接建立其状态监测数据和系统健康状态之间的关系。
基于上述分析,本文提出基于SOM网络的健康状态评估模型。该方法总体思路和其他神经网络方法基本思想类似,首先是神经网络的参数初始化和数据准备,然后利用训练数据对神经网络进行参数训练,最后待训练完成后,将待评估的监测数据输入神经网络,用于系统健康状态评估分析。
然而与其他神经网络的不同之处在于,其他神经网络的构建需要大量不同健康状态下的监测数据用于模型训练,健康状态的评估过程则是以监测数据为输入,直接以对应的健康度为输出;而SOM网络只需要利用健康状态和故障状态的监测数据进行模型训练,待SOM网络的权值收敛稳定后,利用SOM网络的输出值建立当前状态、健康状态和故障状态之间的相对偏离程度,从而确定系统的健康状态。
基于SOM网络的健康状态评估算法的实施步骤如下:
1)在所有工作状态及所有输入信号下,选取控制系统在正常状态以及故障状态通过残差生成RBF网络获得的残差数据。
2)设置SOM神经网络结构参数。
3)对SOM网络进行训练,利用不同工作状态下正常状态和故障状态的残差数据分别构建SOM网络,利用训练好的SOM网络对正常状态和故障状态的残差数据进行聚类,并将其SOM网络输出作为健康度分别为1和0的健康基准。
4)对于待评估状态的残差数据,利用对应工作状态的训练好的SOM网络计算其与竞争层每一个神经元的相似度,并将该相似度而非one-hot编码作为SOM网络的输出,计算该输出与健康基准之间的相对距离,获得此时控制系统的健康状态评估结果。
4 案例验证
针对某型导弹的控制系统进行健康状态评估。该控制系统主要由一级伺服机构、二级伺服机构、主被动雷达导引头、二级综合控制器、弹头伺服机构、战斗弹遥测综合控制器、引爆控制器等组成。共采集该控制系统的6个输入参数以及27个输出参数进行健康状态评估,具体参数如表1和表2所示。考虑到在正常情况下,同一发导弹的检查间隔周期较长,为了获取大量测试数据,收集同一型号不同导弹测试数据进行模型的训练和测试。虽然不同导弹由于处在不同退化过程从而导致健康状态有差异,但是由于同一型号不同导弹具有相同的功能结构、制造工艺和贮存环境,这些导弹在相同退化模式和相同健康状态下,依然具有相似的表现形式和测试数据,即可将这些不同导弹的退化和故障数据看作同一导弹的退化和故障数据。通常导弹检查分为模拟飞行总检查、模拟发射总检查以及全装弹总检查,为了进一步获取不同工作状态下的导弹测试数据,考虑将不同检查状态下的测试数据作为导弹不同工作状态下的测试数据。

表1 6个输入参数

表2 27个输出参数
首先分别构建RBF以及SOM网络结构,其中包括3个残差生成RBF网络、1个自适应阈值RBF网络以及3个SOM网络,分别对应模拟飞行总检查、模拟发射总检查以及全装弹总检查。3个残差生成RBF网络具有相同的3层网络结构,输入层有33个神经元,包括6个输入参数和27个输出参数;隐含层有10个神经元,通过交叉验证方法确定,输出层有27个神经元,对应27个输出参数;自适应阈值RBF网络有3层,输入层有33个神经元,包括6个输入参数和27个输出参数;隐含层有13个神经元,通过交叉验证方法确定,输出层有27个神经元,对应27个输出参数的判别阈值;3个SOM网络也有相同的神经网络结构,其中输入层是一维结构,有27个神经元,竞争层是二维结构,具有×阶的神经元分布,其中的值将根据不同的聚类数目来确定。
考虑到RBF网络共输出27个参数的残差,因此控制系统的故障判据为:若任意某个参数的残差大于其自身的自适应阈值,则控制系统处于故障状态;当所有参数的残差都小于其自身的自适应阈值时,则将该残差输入SOM网络进行健康状态评估。其健康度的定义为
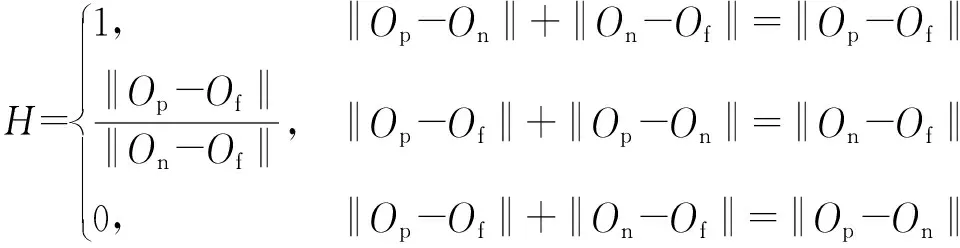
(6)
式中:为故障状态残差数据在SOM网络中的输出;为正常状态残差数据在SOM网络中的输出;为待测残差数据在SOM网络中的输出在和连线上的投影。健康度计算的示意图如图3所示。
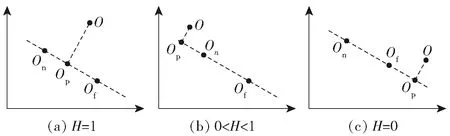
图3 健康度计算示意图Fig.3 Schematic diagram of health calculation
为了方便技术和维修保障人员能够针对不同的健康状态进行针对性后勤保障活动,将健康度分成以下5个健康状态等级,如表3所示。
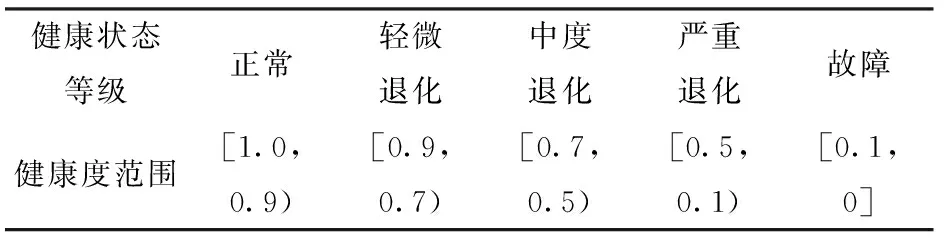
表3 5个健康状态等级
本文选择不同检查状态下导弹控制系统发生的10种故障模式对基于RBF网络的自适应故障观测器的有效性进行验证,验证结果如表4所示。由表4可以看出,本文提出的基于RBF网络自适应故障观测器能够准确地实现导弹控制系统的故障诊断。
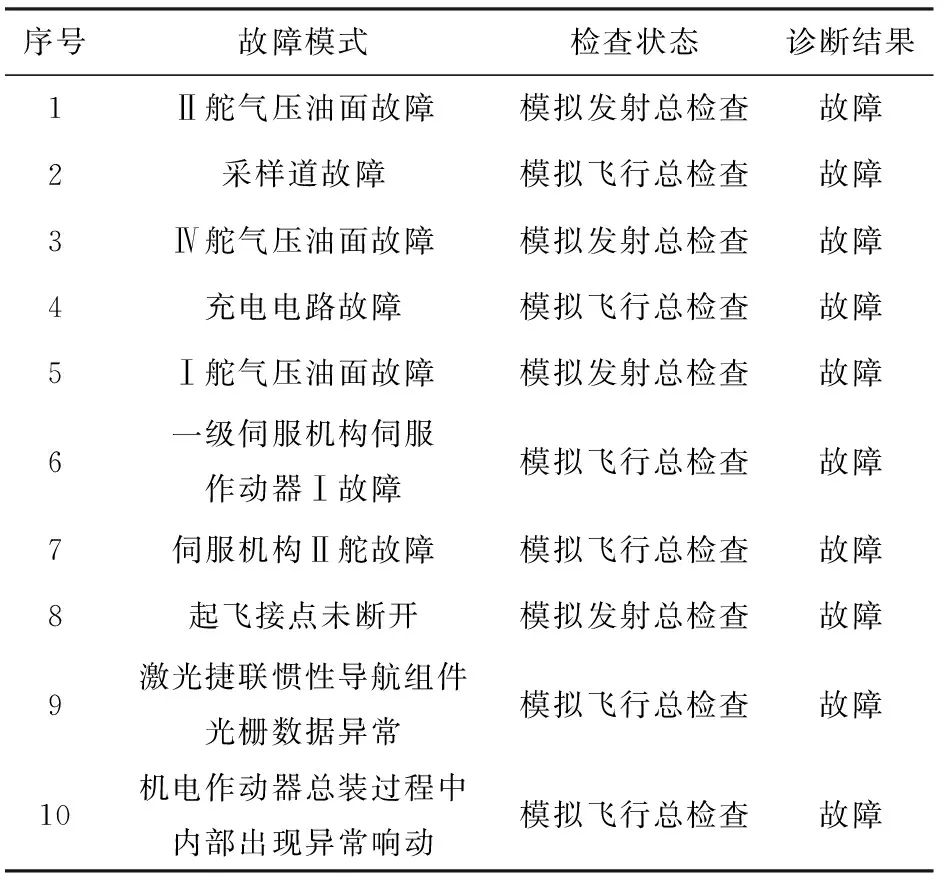
表4 10组故障数据的验证结果
选择10组在同一检查状态下具有不同健康状态的导弹控制系统测试数据,对基于SOM网络的健康状态评估模型的有效性进行验证,其中包括1组正常数据、7组退化数据,以及2组故障数据。SOM网络的输出结果和健康状态评估结果如图4和图5所示。
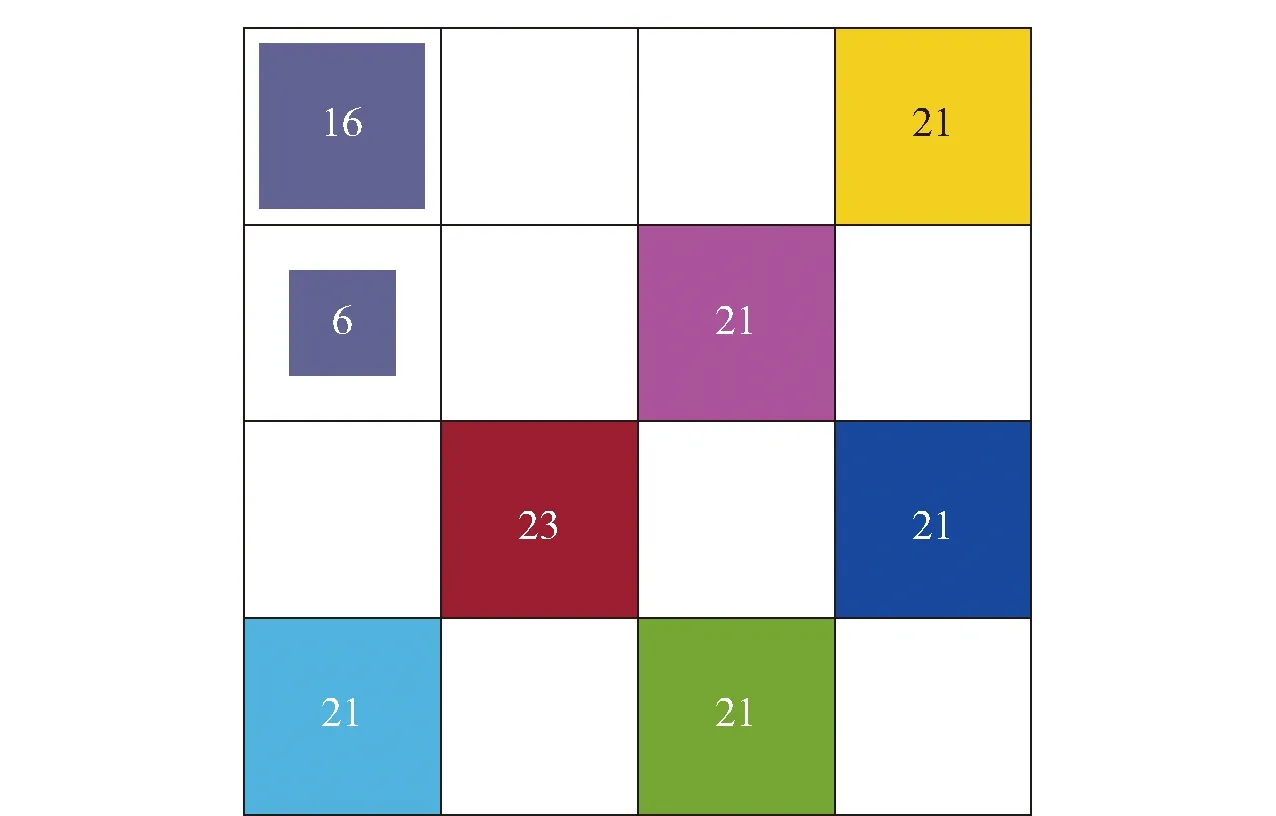
图4 SOM网络的训练输出结果Fig.4 Output results of the training of SOM network
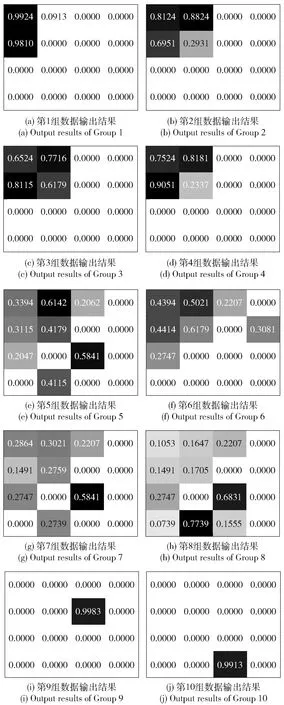
图5 SOM网络的输出结果Fig.5 Output results of SOM network
图4中:16个方格代表竞争层4×4的神经元分布,不同的颜色代表不同的状态类别,数字代表样本的数量;左上角灰色的两个带数字方格代表正常类别,其余6个带数字方格代表6个故障类别。若这16个神经元按照从左到右、从上到下的顺序进行排列,则正常类别和6个故障类别的SOM网络输出分别为
正常类别1:[1,0,0,0;0,0,0,0;0,0,0,0;0,0,0,0];
正常类别2:[0,0,0,0;1,0,0,0;0,0,0,0;0,0,0,0];
故障类别1:[0,0,0,1;0,0,0,0;0,0,0,0;0,0,0,0];
故障类别2:[0,0,0,0;0,0,1,0;0,0,0,0;0,0,0,0];
故障类别3:[0,0,0,0;0,0,0,0;0,1,0,0;0,0,0,0];
故障类别4:[0,0,0,0;0,0,0,0;0,0,0,1;0,0,0,0];
故障类别5:[0,0,0,0;0,0,0,0;0,0,0,0;1,0,0,0];
故障类别6:[0,0,0,0;0,0,0,0;0,0,0,0;0,0,1,0]。
图5是将10组测试数据代入SOM网络的输出结果,其中每个方格数据代表每个神经元的输出结果,颜色的深浅代表输出数值的大小。
由于在SOM网络中包括6个故障类别,根据(6)式,将针对每组测试数据分别计算6个健康度,每组测试数据的健康度为6个健康度计算结果的最小值。SOM网络的健康状态评估结果如表5所示。由表5可以看出,本文基于SOM网络的健康状态评估模型能够准确有效地对导弹控制系统的健康状态进行评估。
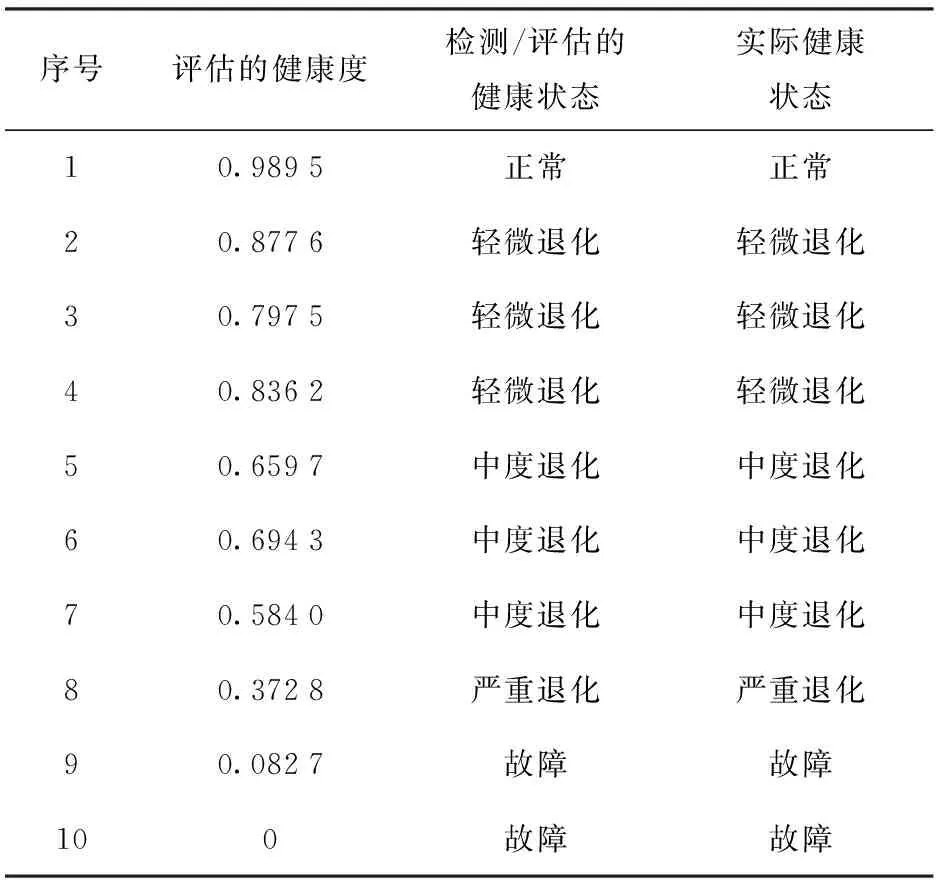
表5 10组数据的验证结果
5 结论
本文提出基于RBF网络的自适应故障观测器和基于SOM网络的健康状态评估模型,分别用于控制系统的故障检测和健康状态评估,通过某型导弹的控制系统案例验证了该方法的有效性。得出主要结论如下:
1)残差生成RBF网络能够对控制系统的输出值进行估计,最终得到实际输出值和估计输出值的残差。
2)自适应阈值RBF网络能够生成随系统状态或者输入指令变化的姿势与故障判别阈值,排除因非故障原因引起的误差。
3)SOM网络能够对控制系统的健康状态和故障状态进行聚类分析,并建立基于健康状态和故障状态监测数据的健康度计算模型。
本文研究对象主要是导弹的控制系统。在未来的研究中,将进一步对导弹其他单机以及整弹的健康状态评估问题进行研究。
