外加阻尼器车床主轴振动抑制方法与实验研究*
2022-05-12凌益民肖长天刘宜杰毛新勇
凌益民,肖长天,刘宜杰,庞 伟,毛新勇,尹 玲
(1.东莞市固达机械制造有限公司,广东东莞 523562;2.华中科技大学,武汉 430074;3.东莞理工科技创新研究院,广东东莞 523808;4.东莞理工学院机器人与智能装备创新中心,广东东莞 523808)
0 引言
数控机床在加工过程中,主轴振动会对加工质量产生较大影响。铣削加工过程发生的振动主要分为强迫振动和自激振动两类。其中强迫振动来源于机床内部的周期激励或外部振源激励,机床外部振源很容易进行抑制,但机床内部强迫振动的振源,如铣刀齿与工件接触瞬间的激振力等很难通过隔离消振;自激振动又称为颤振,是由系统存在的内在反馈引起的,颤振的抑制研究是机床振动抑制的研究重点[1]。目前,抑制机床振动的方法大致可分为被动抑制、主动抑制、半主动抑制3种。其中被动抑制法通过在机床上外加吸振器或质量块的方法来减轻机床部件的振动,没有外界能量供给,而且被动抑制的参数是固定的,难以随工况的改变而变化;主动抑制一般需要外界能量供给,通过传感器检测机床结构的信号并由中央控制器来处理数据,控制抑振部件的参数,主动抑制系统结构精密,能够随着工况实时地用最佳参数抑制制机床的振动;半主动抑制介于被动抑制和主动抑制之间,综合了两者的优点,能够根据工况动态选择控制系统[2]。
1997年陈文锋[3]针对一台高速外圆磨床,通过锤击激励和EMA分析法得到机床结构各阶模态振型,对比发现机床液压电机是最主要的振源,在将齿轮泵改为螺杆泵并将油箱移动至床身外部后,液压电机的振动有效地被抑制。2004年崔涛等[4]利用电磁激振器对TH6350数控卧式加工中心施加随机脉冲信号,并由EMA法分析出机床结构的模态参数及振型,辨识出了在该激励下主轴箱系统是整个机床的薄弱部件,他将粗糙的主轴打磨光滑后再次用同样的激励信号进行实验,结果主轴的振型明显减小,表明该优化方法是有效的。2004年Altintas[5]通过机床静态下的锤击实验得到了刀具的频响函数,以此来分析切削加工的稳定性。2006年John[6]为了减小加工过程中机床结构的振动,在立式铣刀内部加入弹性阻尼片来提高刀具的刚度,通过仿真实验指出,并不是弹性阻尼片越多刀具振动的强度越小,而是存在一个最优解,当弹性阻尼片数量达到这个值时效果最好。2008年华中科技大学的卢艺扬[7]以XHK5140型数控机床为研究对象,通过编程使机床工作台的随机运动来激励机床,并分析机床立柱的动力学参数,结果表明立柱的前5阶固有频率和振型均与锤击实验辨识出的数据吻合。2011年Mahr F等[8]在利用频谱分析铣削加工稳定性的研究中指出,多个颤振频率可能同时出现在机床的不稳定的铣削过程中,这些颤振频率的位置反映了机床的薄弱模态,在随后的研究中他们指出薄弱模态会随着加工参数的变化而变化,如主轴的转速和刀具的进给速度等。2013年Yutaka等[9]同样设计了一种包含阻尼芯的减振装置,将其安装在立式铣刀的夹头上后进行实验,结果表明该装置能够提高刀具系统的稳定性,减少铣削加工过程中刀具的振动幅度。2015年Munoa[10]提出一种利用机床的进给系统和加速度传感器来主动抑振的方法,有效地提高系统切削加工时的稳定性和生产效率。2018年Krishnan[11]研究了铣削加工过程中的过程阻尼对高频模态的影响,表明过程阻尼抑制了高频模态的振动,高频模态可以通过过程阻尼来稳定。
本文将以华中科技大学的VMC850E型立式数控加工中心为研究对象,针对车床加工中出现的振动问题,提出一种阻尼器的设计,并研究将该阻尼器加装在机床后,对机床加工时的振动和加工零件表面质量的影响。
1 外加阻尼器对车床主轴振动抑制研究
1.1 外加阻尼抑振原理
1.1.1 外加阻尼器结构
主轴长期使用后,表面磨损、生锈等因素会导致主轴的结构不对称,因此在工作的工程中振动强度增加,成为机床系统的薄弱部件。为了避免主轴剧烈的振动,换新主轴是一个办法,但VMC850E型立式数控加工中心的主轴通过螺栓固定在滑台底部,内部又包含电机等部件,拆卸极为困难。考虑到实验机床的结构及实际生产过程,需要一种避免频繁更换主轴又能有效抑制主轴震动的方法。基于机床存在的上述问题,本文设计了一种在外部将阻尼材料与主轴固定形式的阻尼器,其模型如图1所示。由图可知,本文所设计的外加阻尼器,其基本工作原理是:通过紧固件将弹性阻尼材料包裹在机床主轴四周,并使用螺栓固定,通过改变螺栓的松紧来改变阻尼大小。外加阻尼器可简化成一个质量-阻尼-弹簧系统,弹簧-阻尼系统可以存储和消耗主轴振动时的能量从而减弱主轴的振动强度。图2所示为外加阻尼器的实物图,图3所示为外加阻尼器后的主轴动力学模型。

图1 外加阻尼器模型

图2 外加阻尼器实物

图3 外加阻尼器后的主轴动力学模型
为了研究外加阻尼器对主轴振动的抑制效果及原理,本文对实验机床主轴在外加阻尼器与不外加阻尼器的情况下,分别进行主轴随机启停的空运行实验和工件实际切削实验。图4所示为外加阻尼器后的机床主轴。

图4 外加阻尼器后的机床主轴
1.1.2 机床阻尼动力学方程
考虑到在实际加工过程中,机床主要激励来源于刀具和工件的相对运动,在侧铣加工中,由于一次走刀主轴的转速通常是恒定的,所以这是一种周期激励。考虑主轴外加阻尼器时,机床成为一个有阻尼多自由度系统,其运动微分方程如下所示:

式中:F(t)为切削时机床系统的激励力;T为周期,与主轴转速和刀具刀刃数有关,主轴转速越高、刀具刀刃数越多,则T越小。
将切削激励力展开为傅里叶级数形式,有:

式中:ω为激励信号的基频,ω=2π/T,基频的整数倍jω代表谐频。
式(2)表明一个周期激励可以分解成一系列谐频的简谐信号叠加。式中aj、bj、a0由下面两式确定:
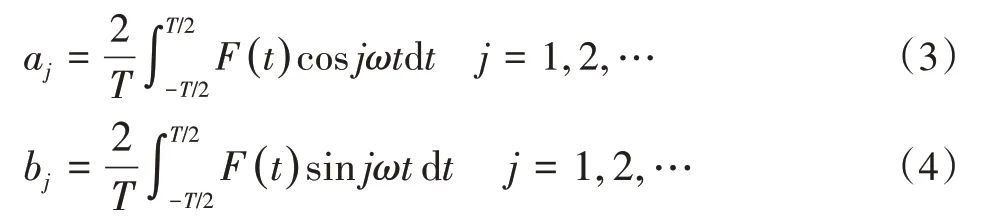
式(3)、(4)分别代表第j个简谐分量中cosjωt和sinjωt的参与程度,对应于每一个激励分量的运动微分方程,有:
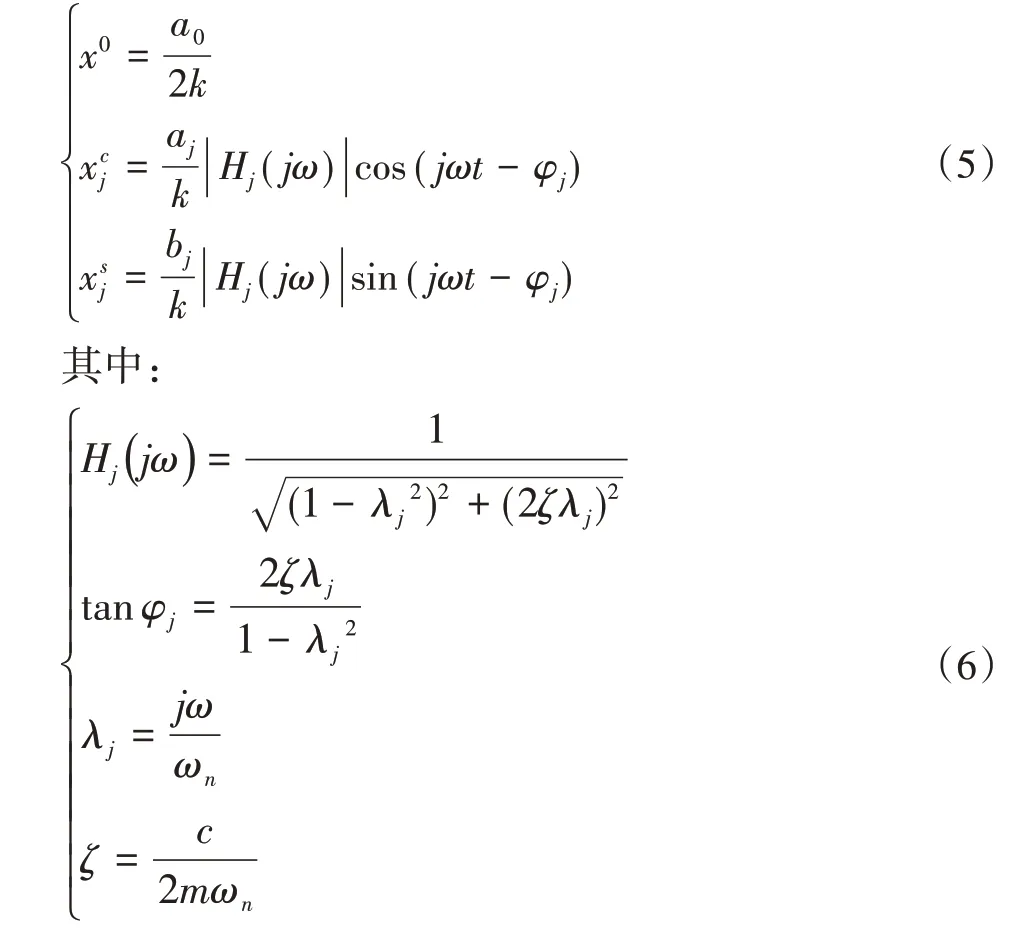
将式(3)~(6)代入式(1),得到周期激励下有阻尼系统的稳态响应:
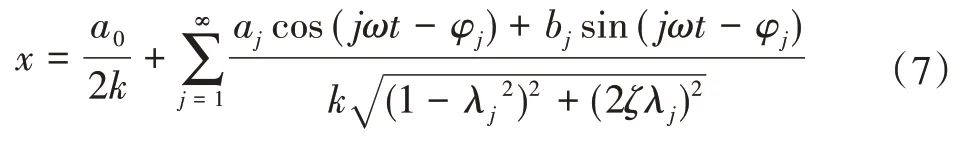
从式(7)可以看出,主轴在切削激励下的响应信号与机床固有频率、阻尼大小、阻尼质量有关,其中机床的固有频率由机床自身的结构决定,一台特定机床的固有频率是不随外部激励力的变化而改变的。同时外加阻尼器的质量和大小也是影响主轴响应信号的因素,相比于无阻尼的情况,系统外加阻尼器时由于分母(2ζλj)2的存在,降低了自由度的振幅信号,也就抑制了主轴的振动强度。
1.2 外加阻尼器对主轴抑振效果的研究
从主轴的空运行实验出发,通过主轴的响应信号差异,验证阻尼器对主轴的减振效果,并研究外加阻尼器质量、外加阻尼大小对主轴振动的抑制效果。为了排除外加阻尼器对主轴3 000 r/min转速下振动抑制效果的偶然性,作为对照设计了主轴在1 000 r/min、2 000 r/min转速下的空运行实验。
1.2.1 外加阻尼大小对主轴响应信号的影响
外加阻尼器通过两个紧固件将弹性材料固定在主轴四轴以达到附加阻尼的目的。本实验中通过螺栓调整阻尼器紧固件之间距离d来改变外加阻尼大小,设定紧固件距离d的值分别为33.9 mm、33.0 mm、32.1 mm来表示外加小阻尼、外加中阻尼、外加大阻尼3种情况。外加阻尼器的紧固件距离d的标注如图5所示。

图5 外加阻尼器紧固件距离d
为了研究外加阻尼大小对主轴振动的抑制效果,要排除外加阻尼质量的影响。实验中使用两个外加阻尼器并调整两个阻尼器紧固件距离d值分别为33.9 mm、33.0 mm、32.1 mm时进行主轴随机启停实验。在主轴转速为1 000 r/min、2 000 r/min、3 000 r/min时3种外加阻尼大小与无阻尼时主轴的响应信号对比分别如图6所示。图中在主轴不同转速下的蓝色曲线代表无外加阻尼时主轴的响应信号,红色曲线代表外加阻尼后主轴的响应信号。对比上述3组图可知,在同样的外加阻尼条件下,主轴的响应信号幅值随着主轴转速的增加而增加,即转速越快,主轴的振动强度越高;在同样的转速条件下,主轴无外加阻尼的响应信号幅值都是最大的,外加阻尼后主轴的响应信号都有所降低,并且主轴响应信号的降低幅度随外加阻尼大小的增加而增加,对比主轴无外加阻尼和外加大阻尼两种状态,主轴的响应信号幅值降低了近50%。由此可见外加阻尼器能够抑制主轴的振动强度,随着外加阻尼大小增大,主轴的振动强度被抑制得越明显。


图6 不同主轴转速时响应信号对比
1.2.2 外加阻尼质量对主轴响应信号的影响
外加阻尼的质量同样是影响主轴振动的因素,本节研究不同外加阻尼质量对主轴振动强度的影响。改变外加阻尼的质量能够通过附加不同数量的阻尼器来实现,在主轴上外加1个、2个完全相同的阻尼器时如图7所示。

图7 主轴外加阻尼器
为了研究外加阻尼质量对主轴振动的抑制效果,需要控制外加阻尼大小相同。实验设置主轴在1 000 r/min、2 000 r/min、3 000 r/min三种转速下时,检测无外加阻尼器、外加1个阻尼器、外加2个阻尼器时主轴的响应信号。为了控制外加阻尼大小这个因素,实验中控制阻尼器紧固件距离d=33.0 mm(对应中阻尼情况)。主轴在上述3个转速下,分别外加1个阻尼器、外加2个阻尼器与无外加阻尼器的主轴响应信号对比如图8所示。图中在主轴不同转速下的蓝色曲线代表无外加阻尼时主轴的响应信号,红色曲线代表外加不同数量的阻尼器后主轴的响应信号。对比上述3组图可知,在3个转速下主轴随机启停运动时,外加1个、外加2个阻尼器的主轴响应信号幅值较无外加阻尼都有所降低。对比每个转速下的主轴响应信号可知,2个外加阻尼器对主轴的振动抑制效果要优于1个外加阻尼器,但是主轴的响应信号幅值差异不大,相差在5%以内。

图8 不同主轴转速时3种阻尼情况下响应信号对比
从以上两组实验可以发现,外加阻尼器能够有效抑制主轴的振动,这表现在外加阻尼器后主轴的随机启停激励的响应信号幅值降低。外加阻尼器的大小和质量都是影响抑制主轴振动的因素,改变阻尼大小比改变阻尼质量对主轴振动的抑制效果更为明显:通过改变螺栓的松紧改变外加阻尼的大小,在设定的3种外加阻尼大小范围内,每次增加阻尼大小能够减少主轴响应信号幅值15%左右,在外加阻尼最大时与无阻尼相比,主轴振动信号强度降低了一半;改变外加阻尼器数量来改变外加阻尼的质量,外加2个阻尼器对比外加1个阻尼器,主轴的振动信号有略微减少,减少幅度只在5%以内。
1.3 外加阻尼器对主轴模态的影响
通过主轴随机启停空运行实验表明,外加阻尼器能够有效减少主轴的振动强度,并且外加阻尼大小比外加阻尼质量对于抑振效果有更明显的影响。本节通过锤击实验获取主轴在外加阻尼器时的模态参数,并分析外加阻尼器对主轴的抑振机理。因为外加阻尼大小较外加阻尼质量对主轴的振动抑制效果更明显,实验中只通过紧固件距离d调节阻尼大小而不改变阻尼器数量。在主轴上外加2个阻尼器,并且分别调整紧固件距离d值为33.9 mm、33.0 mm、32.1 mm来表示外加小阻尼、外加中阻尼、外加大阻尼3种情况,通过锤击分析法获取主轴外加阻尼器后的模态参数。实验的布置与1.2.1节介绍的未加阻尼器实验相同,实验中锤击刀柄X方向,得到不同条件下主轴的模态稳态图如图9所示。
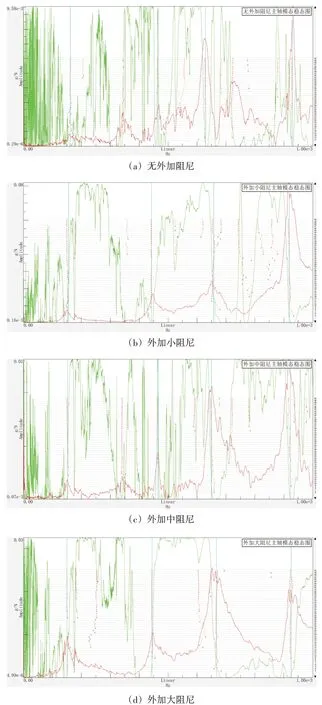
图9 不同条件下主轴模态稳态图
根据主轴不同状态下的稳态图,利用LMS软件里面的PolyMAX算法辨识出主轴在0~1 000 Hz频带范围内的各阶模态,得到无外加阻尼和有外加阻尼下主轴的固有频率和阻尼比,如表1所示。

表1 有无外加阻尼下主轴的模态参数对比
通过表1的数据对比分析可以得出,外加阻尼器使得主轴结构的模态参数发生了改变。实验中分析的频率范围是0~1 000 Hz,考虑到分析的频带范围较大,实验中辨识的模态参数可能与真实模态参数之间存在误差,经验表明两次结果的模态参数在20 Hz以内就认为是同一阶模态,反之则认为是固有频率发生了变化。从固有频率从的角度分析,有阻尼时主轴1阶模态固有频率比无外加阻尼时主轴固有频率大,且随着外加阻尼的增大逐渐增大,但总体来说变化不大,仍为同一个固有频率;有外加阻尼时主轴2阶模态固有频率相较与无阻尼时也更大,但并没有和阻尼的增大形成线性的关系;有阻尼时主轴3阶模态固有频率则小于无阻尼时固有频率;有阻尼时主轴4阶模态固有频率在外加大阻尼时高于未加阻尼时主轴的固有频率,外加小阻尼、外加中阻尼时则低于未加阻尼时主轴的固有频率。上述实验表明,外加阻尼器对主轴的振动抑制效果明显,表现在主轴的低阶模态的固有频率有所提高。详细来说,在外加小阻尼、外加中阻尼、外加大阻尼3种情况下,主轴的第1阶模态固有频率分别提高了6.465 Hz、8.598 Hz、11.995 Hz;主轴第2阶模态固有频率虽然没有随着外加阻尼大小的增加而增加,但相较于无阻尼时固有频率都有所提高。从阻尼比的角度来分析,除了主轴第二阶模态外加小阻尼时的阻尼比大于外加中阻尼时的阻尼比,随着外加阻尼大小的增加,主轴4阶模态对应的阻尼比也有所增加,并且外加阻尼器后主轴各阶模态的阻尼比均大于无阻尼时的阻尼比。由此可见见外加阻尼器不仅能影响主轴的固有频率,同时提高了系统的阻尼比。
2 外加阻尼器对切削加工影响研究
2.1 外加阻尼器
主轴的随机启停空运行实验表明外加阻尼器能够有效减小主轴的振动响应信号,锤击实验表明外加阻尼器能改变主轴的模态参数,并且外加阻尼越大时,主轴的振动抑制效果越明显。但是空运行实验无法表征机床在实际切削激励下外加阻尼器对主轴的抑制效果。因此本章将进一步研究机床的实际切削加工,根据主轴的响应信号来验证外加阻尼器对主轴的抑制效果;深入研究切削加工过程实验中主轴的模态,采用ODS模态解耦法来分析主轴各阶模态对加工振动的影响程度,对比不同外加阻尼大小时主轴的主振模态变化情况;通过零件表明成型质量来研究外加阻尼器是否能改善工件成型质量。
2.2 主振模态辨识原理
机床的各阶模态通常没有主要次要之分,通常情况下所说的1阶模态、2阶模态到n阶模态只是按照其固有频率大小来排序的[12]。机床受到不同带宽的信号激励时,在激励带宽内的机床各阶模态的参与程度实际上是不相同的,因此在实际切削加工过程中,不同的工况下表现出的激励是不同的,机床表征出的动力学特征也不同。激励影响机床表征出的动力学特性,在机床各阶模态中对机床动力学特性有主导影响的模态称为主振模态(Dominant frequency vibration)。研究机床整机动力学特性需要通过满足频带宽度范围的激励源来激励机床,从而辨识出机床的模态参数。
2.2.1 ODS模态解耦原理
工作变形形状(Operational Deflection Shapes,ODS)是用来研究主振模态的方法,ODS利用振动响应信号是各个模态线性叠加的原理,对模态进行解耦,用各阶模态与参与系数积的线性叠加来表示某个频率下机床的变形,来计算机床各阶模态在某一个激励下对振动的影响程度,其中具有最大参与系数的那一阶模态就是主振模态。有别于模态振型,ODS是随着加工工况的改变而变化的,而模态振型是系统的固有属性,由机床的结构决定,一阶模态对应着一个固有频率和模态振型。ODS分析法又分为基于时域信号的分析法和基于频域信号的分析法,其中基于时域信号的分析法针是在某个时刻分析各阶模态对机床结构振动的贡献度;基于频域信号的分析法则分析某个频率下各阶模态对机床结构振动的贡献度,又可细分为频谱或互功率谱上的频域分析。在频谱上分析得到的是各个测点之间的相位关系,振型代表各个测点的实际振动;在互功率谱上分析得到的是各个测点同参考点之间的关系,振型代表各个测点同参考点之间的相对运动关系。本文主要用过在频谱和功率谱上的两种分析方法来获取机床的主振模态,考虑到频响函数和模态参数的关系,有:
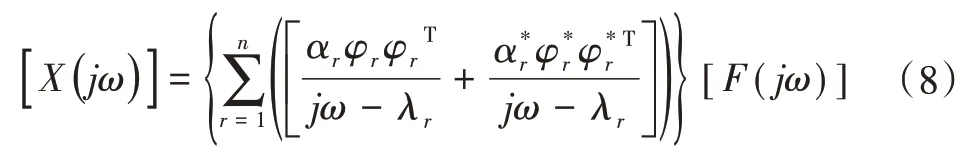
此时的系统响应就改写成各阶模态与参与系数积的线性叠加形式。可以看出,系统的ODS也会随着激励力的变化而变化。相较于系统的频响函数,ODS反映的是系统在外部激励下系统某个频率下的变形,因此是一个向量,与系统的关系不是一一对应的,而固有频率反映系统的固有属性,由系统的结构决定,与外部激励无关。由于系统的各阶振型向量的正交性,通常将其作为系统模态空间的一组坐标基向量,用振型来表示系统在各个频率处的变形得到系统的ODS方程:
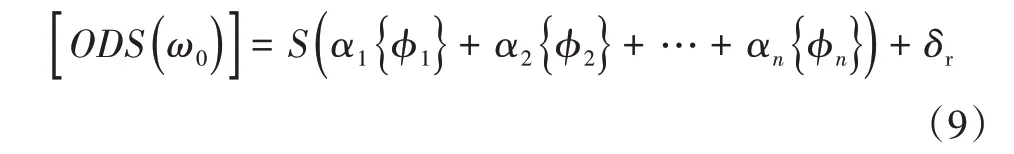
式中:ODS(ω0)为激励力频率为ω0时系统的ODS;为系统的第1~n阶振型;S为一个常量,用来归一化参与系数;δr为参与误差,ODS分解精度越高则δr值越小;αi为各振型的参与系数,其中最大的αi代表该阶振型的贡献量最大,其对应的模态就是系统的主振模态。
2.2.2 基于ODS的主振模态辨识
LMS信号采集系统的Operational Deflection Shapes&Time Animation模块可以进行ODS分析,其中spectrum参数代表在频谱上的分析,其相位信息代表各个测点的相对运动关系,体现了各个测点的振动情况,此时的ODS振型表示结构的实际振动状态;crosspower参数代表在互功率谱上的分析,此时的ODS振型表示各个点同参考点之间的相对运动关系。选取以上两个参数作为分析数据来分析切削加工过程中的主振模态识别过程,spectrum和crosspower的理论计算方程分别表示如下:
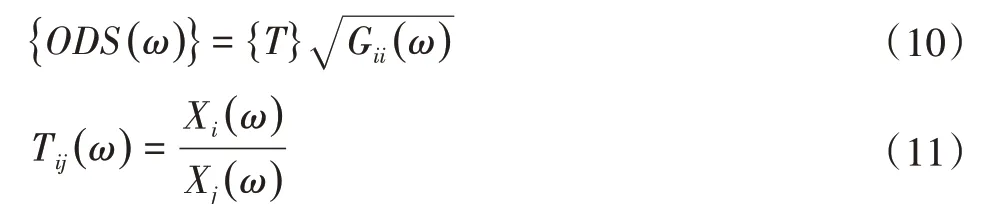
式中:传导函数Tij(ω)为非参考点响应信号Xi(ω)与参考点响应信号Xi(ω)的比值,通过参考点的自功率谱和传导函数Tij(ω)得到其他测点结构的ODS。
由上述公式推导分析可知,分解各阶模态的步骤如下:(1)获得机床在特定位置下的各阶模态和振型向量,通过EMA分析法获取机床静态下的前4阶模态和对应的振型向量;(2)分别在主轴外加阻尼前后进行空运行和切削实验,通过频域分析法获取机床在切削加工状态下具有最大能量处的ODS变形;(3)通过上述公式计算各阶模态对ODS变形的影响程度,最大参与系数对应的模态就是该激励下的主振模态;(4)对比主轴外加阻尼前后的主振模态,分析研究外加阻尼器对切削加工过程的影响。
2.3 外加阻尼器的切削加工实验
2.3.1 实验方案
为了探究外加阻尼器在切削实验中对主轴的振动抑制效果影响和工件成型质量影响,首先在主轴未加阻尼器的情况下进行工件的常规切削,并在加工参数完全相同的情况下,在主轴上外加阻尼器并改变阻尼大小进行切削加工,加工方式为铣削工件侧面,进行主轴不外加阻尼器的切削实验、主轴加装阻尼器并调节阻尼大小,在同样的切削参数下对相同形状的工件切削实验。本组实验将阻尼紧固件的距离分别调整为33.9 mm、33.0 mm、32.1 mm时,研究阻尼器大小对切削加工过程的影响。
针对上文中提出的实验方法进行如下实验设置:传感器的布置除了刀柄处的参考测点被取下其余均与1.3.2小节中相同;合金铣刀的规格参数:刀刃直径18 mm、刀刃长度45 mm、总长度100 mm、螺旋角35°;实验中用到的工件实物图和机床现场布置如图10~11所示,加工参数如表2所示。

图10 工件实物

图11 机床现场布置

表2 切削加工参数
分别在机床主轴无外加阻尼器,外加小阻尼、中阻尼、大阻尼(对应的外加阻尼器紧固件距离d值为33.9 mm、33.0 mm、32.1 mm)4种加工条件下,使用表2所示的加工参数,对4个与图10所示完全相同的工件进行切削加工实验,检测主轴的响应信号。
2.3.2 主轴主振模态分析
(1)主轴响应信号分析
图12所示为无外加阻尼和外加小阻尼、中阻尼、大阻尼时的切削过程中主轴的响应时域信号对比。图中的峰值部分代表刀具切削工件时主轴的振动信号,边缘部分代表走刀时主轴的振动信号。对比4幅图可以看出,加工过程中机床走刀时的激励相较于切削时的激励可以忽略不计,主轴在3 000 r/min的转速和表2所示的加工参数下,外加阻尼越大则主轴的振幅越小,在阻尼调至最大时(外加阻尼器紧固件距离d=32.1 mm),主轴的切削振幅下降了近50%。

图12 不同条件下主轴的时域信号
(2)主轴的主振模态分析
为了分析不同外加阻尼大小的切削实验中主轴的主振模态,需要获取机床的ODS。通过FRF、互功率谱、时域信号等参数都可以获取结构的ODS,这里采用频谱作为信号源,频谱上分析得到的是各个测点之间的相位关系,振型代表各个测点的实际振动,LMS内的ODS模块采用所选频带内幅值最大的频率来计算结构的ODS,得到在不同外加阻尼条件下主轴的ODS如图13所示。

图13 不同外加阻尼条件下主轴的ODS
在刀具和工件相对运动稳定后研究切削过程的振动,通过LMS前端信号采集系统检测的信号,获取主轴在不同外加阻尼条件下的频谱进行ODS分析,得到主轴幅值-频率函数如图14所示。
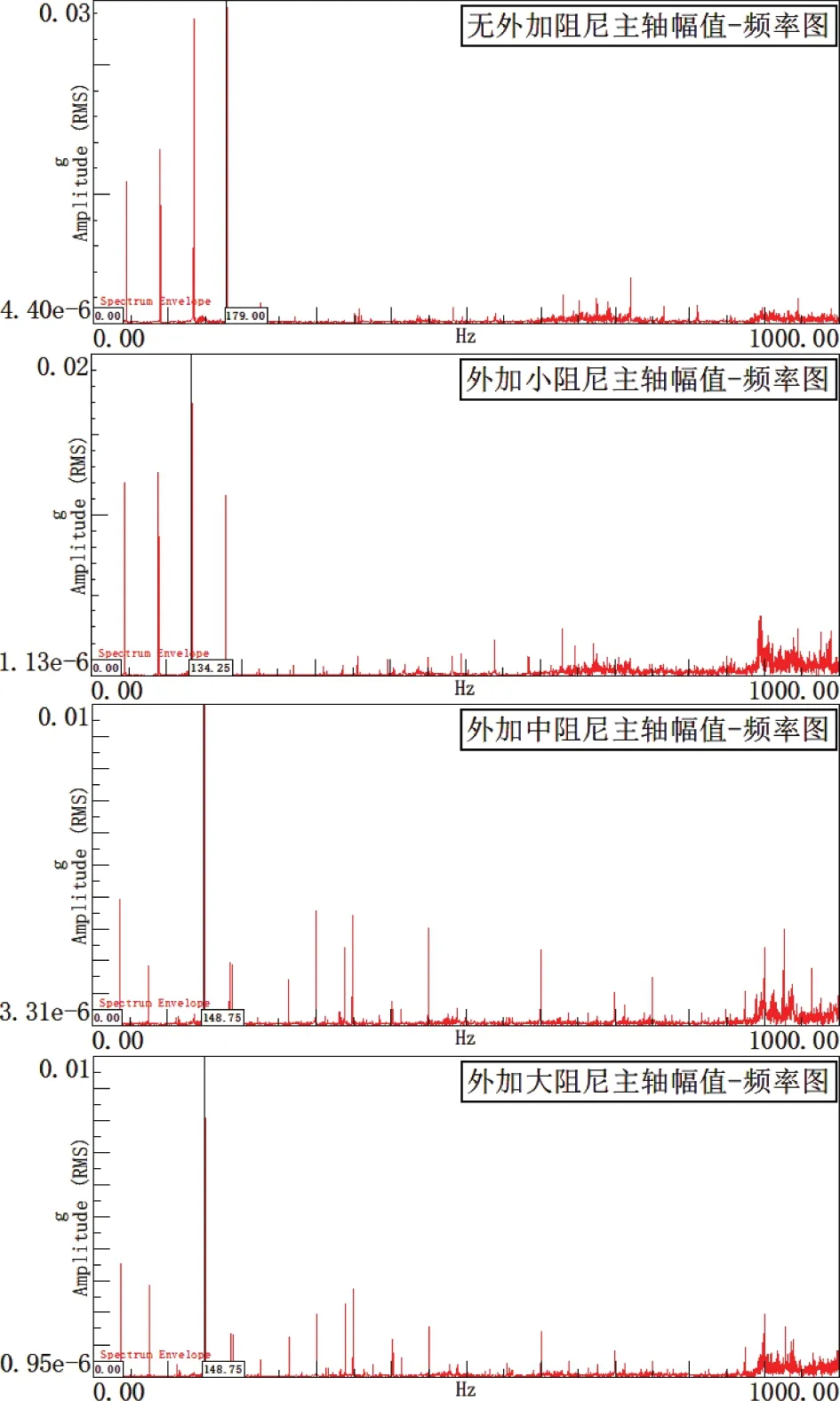
图14 不同阻尼大小下主轴振动幅值-频率曲线
考虑到机床低频振动对加工影响更大,因此此处选择0~100 Hz频率范围内,使主轴振动幅值最大处的频率进行ODS分解,4种状态下所选频率如表3所示。表中的频率并非主轴的固有频率,而是在切削实验中振动能量最大处对应的频率,是主轴各阶模态共同作用的结果。从上图可以看出,在外加阻尼大小相同的条件下,主轴的前3阶模态对ODS变形的影响最大,而第4阶模态对ODS变形的影响相对来说较小。

表3 振幅最大处的频率选择
通过上述实验获得切削状态下主轴各阶模态对主轴振动能量最大处频率的分解系数,如图15所示。机床工作中振动的模态往往是低频模态,这也验证了在模态分解中低频模态具有很大的分解系数。根据结果可知,在外加阻尼大小变化的情况下,随着外加阻尼大小的增加,固有频率最低的一阶模态的分解系数具有明显的减小趋势,二、三阶模态的分解系数则逐渐变大,四阶模态没有明显的单调变化性,但是总体来说占比很小。由此可见,外加阻尼器改变了各阶模态对ODS变形的影响程度,尤其是削弱了第一阶模态的影响程度。
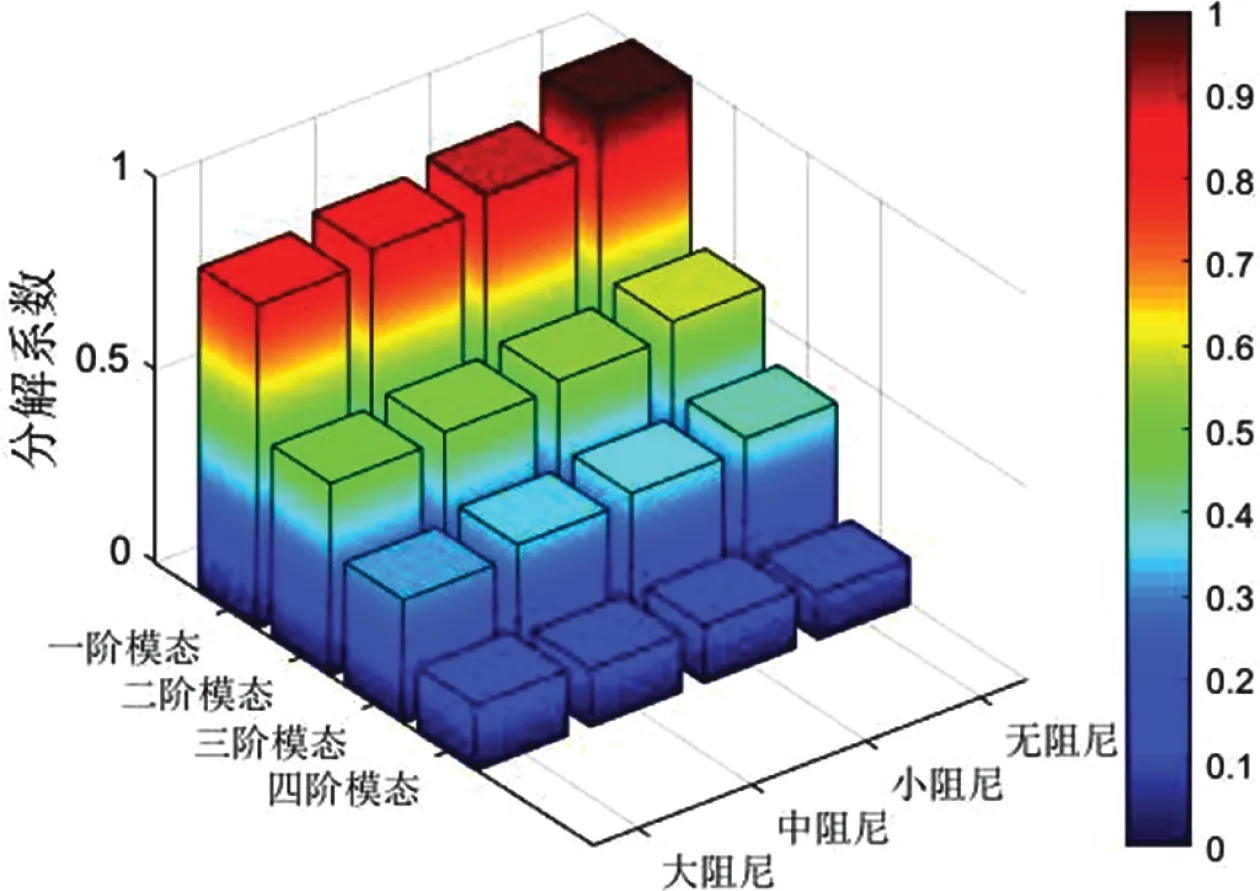
图15 不同外加阻尼大小条件下的模态分解系数
(3)零件成型质量对比
在无外加阻尼和3种外加阻尼大小的加工条件下,工件切削加工的表面如图16所示。

图16 不同条件下工件表面质量对比
对比在4种加工状态下工件的侧表面成型质量,无外加阻尼时,工件成型质量最差,表面有明显的振纹,甚至出现了毛刺;外加小阻尼时,工件成型质量有所改善,没有毛刺出现,但是还是有比较明显的振纹;外加中阻尼时,工件成型质量进一步改善,表面较为光滑,只有不明显的振纹;外加大阻尼时,工件成型质量最好,表面十分光滑,振纹几乎不可见。通过加工零件的表面质量可知,外加阻尼器对主轴振动的效果比较明显,能够显著改善加工质量,在实验所用到的加工参数下,外加阻尼越大则工件侧表面越光滑。
3 结束语
本文基于有阻尼系统强迫振动的位移的理论,针对车床在加工过程中主轴出现较大振动影响加工质量的问题,提出了在主轴外加阻尼器来代替传统更换主轴以减小主轴振动强度的方法,设计了一种易于拆卸的外加阻尼器,进行了空载主轴随机旋转实验、锤击实验与实际工件切削实验,研究了阻尼大小与外加阻尼质量对抑振效果的影响。实验结果表明,本文所设计的外加阻尼器能抑制主轴的振动,且外加阻尼大小越大、外加阻尼质量越大、抑制效果越明显。同时,本文的实验表明,外加阻尼大小比外加阻尼质量对抑振效果的影响更明显。
