基于CATIA 和ANSYS 的电动摩托车车架强度仿真分析*
2022-05-12杨润泽文少波许屹洲
杨润泽 文少波 许屹洲
(南京工程学院汽车与轨道交通学院 江苏 南京 211167)
引言
近年来,由于安全、绿色环保逐渐成为社会的主题,在摩托车方面,燃油摩托车将逐渐退出市场,电动摩托车将成为有效替代品。车架作为电动摩托车的核心部件,固定支撑着电池、电机、传动系统、悬架等部件,且在行驶过程中承受各种载荷。车架性能的优劣直接影响到安全性、乘坐舒适性和整车寿命。车架在使用过程中,如果应力过大,则车架安全性低;如果应力过小,则车架强度会有较大的冗余量,会增加电动摩托车的生产成本。因此,分析电动摩托车车架的结构强度,在保障车架使用安全性的前提下控制制造成本,具有很高的工程实用价值[1]。
传统车架设计需要进行台架试验和现场测试,导致投入过多、研发周期过长。随着计算机软件技术的成熟,利用软件对产品进行设计与仿真分析成为一种可靠且有效的设计方式。本文采用CATIA 和ANSYS 软件相结合,综合CATIA 软件的建模能力和ANSYS 软件的有限元分析与仿真模拟能力,进行电动摩托车车架的静力学分析。
1 电动摩托车车架三维模型的建立
在CATIA 软件中建立电动摩托车车架三维模型,为了保证分析的效率,对车架模型进行合理简化,重点分析对车架强度影响较大的部件。在结构简化过程中,根据部件承受应力情况分为承载件、非承载件,保留位于较高应力区的承载件,如车架主管、支管、电机上支撑管、电机下支撑管、前撑管等。对于非承载件,如安装空洞、固定螺栓、外壳等,因其对有限元计算影响小,进行适当合并或者去除[2]。本文设计的电动摩托车采用双摇篮车架,结构简化后,在CAITA 软件中建立的三维模型如图1 所示。
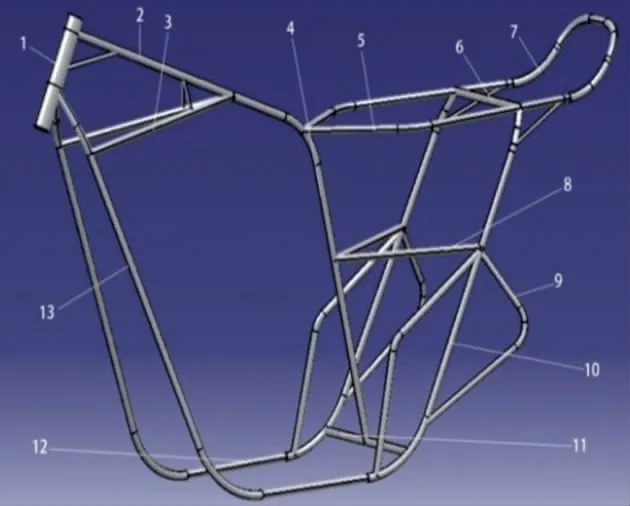
图1 电动摩托车车架三维模型
2 车架有限元模型
2.1 材料设置
车架材料选择Q235 钢,进入ANSYS workbench,选择Static Structural 模块进行车架材料的弹性模量、泊松比、质量密度、抗剪模量、张力强度、屈服强度设置。车架材料的主要属性如表1 所示。
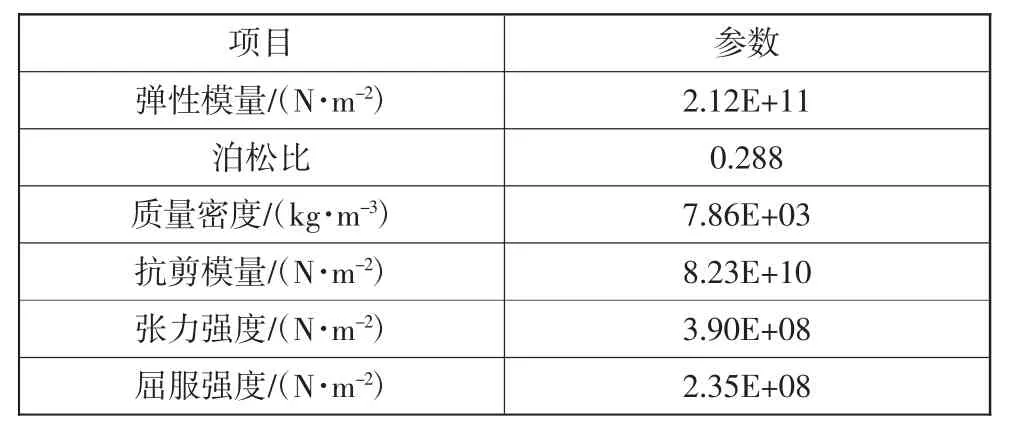
表1 车架材料属性
2.2 有限元模型的修整
电动摩托车车架由不同截面的钢管焊接而成,将在CATIA 软件中建立的车架模型导入Geometry模块进行几何清理,消除边界错位和车架弯管处的缝隙,压缩相邻曲面之间的边界,以提高有限元分析的准确性。
2.3 有限元模型的网格划分
与构件长度相比,钢管的管径和壁厚很小,在此情况下使用六面体实体单元,虽然精度很高,但是网格划分困难、计算时间过长,因此对管件采用多域扫掠型(MultiZone)网格划分法[3],单元尺寸设为5 mm。划分好的网格如图2 所示,包含2 052 个单元,4 088个节点。

图2 车架有限元网格划分
3 车架的强度仿真分析
针对车辆使用过程中的弯曲、制动、转弯、碰撞4 种典型工况,分析车架在受到来自外部载荷以及整车加速度突变后所产生的应力与位移,作为校核车架结构强度的依据[4]。
3.1 静态载荷
车架所受的静态载荷包括车架、驾驶员、电机、电池、车身、传动系总成以及转向与制动系统总成的质量。载荷添加时,车架质量采用重力场形式,其他负载可以简化为施加在各连接处的集中载荷或均布载荷。车架质量和主要零部件的质量以及处理方式见表2,静态载荷加载状况如图3 所示。

图3 静态载荷加载状况

表2 车架负载情况kg
3.2 边界条件
本电动摩托车采用双减震器式后悬架,每个减震器通过2 个焊接铰链与车架相连。对车架进行强度分析时,通过约束车架和悬架连接点的平动自由度来模拟整车的实际约束情况。选取减震器上下2个铰链与车架的连接点作为约束点,即对4 个点施加平动自由度约束,释放全部转动自由度。边界条件约束如图4 所示。
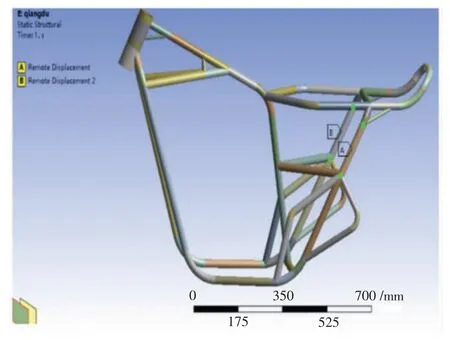
图4 边界约束条件
3.3 工况分析
3.3.1 弯曲工况
车架的弯曲工况是模拟电动摩托车静止或在良好路面上匀速行驶时的状况[5]。车架在承受负载的同时会受到路面的反作用力从而产生弯曲变形。
模拟弯曲工况时,车架承受的静态载荷要乘以动载因数。动载因数一般为2.0~2.5,在此取2.0。弯曲工况下车架的边界约束条件如表3 所示。

表3 弯曲工况车架边界约束条件
经过有限元分析与计算,电动摩托车车架在弯曲工况下的位移与应力云图分别如图5 与图6所示。

图5 车架弯曲工况位移云图

图6 车架弯曲工况应力云图
从图5 可以得知,车架最大位移出现在悬架支撑管的弯曲处,为0.36 mm。
从图6 可以得知,最大应力出现在上横管与边管连接处,为35.04 MPa。主要原因是此处为多个管件连接处,容易出现应力集中现象,会产生较大的应力。与管件材料Q235 钢材的屈服极限235 MPa 相比,车架整体应力分布水平适中。
3.3.2 制动工况
车架制动工况是模拟电动摩托车在行驶过程中紧急制动时的状况。电动摩托车车架除了承受驾驶员与车身负载的重力作用,在制动时还受到纵向制动惯性力的作用。制动加速度和摩托车总质量决定惯性力的大小[6]。
制动工况的边界约束条件与弯曲工况的约束条件相同,但是需要在车架弯曲工况计算的基础上对车架加载1.4g 的制动加速度。
经过有限元分析与计算,该车架在制动工况下的位移与应力云图分别如图7 与图8 所示。

图7 车架制动工况位移云图
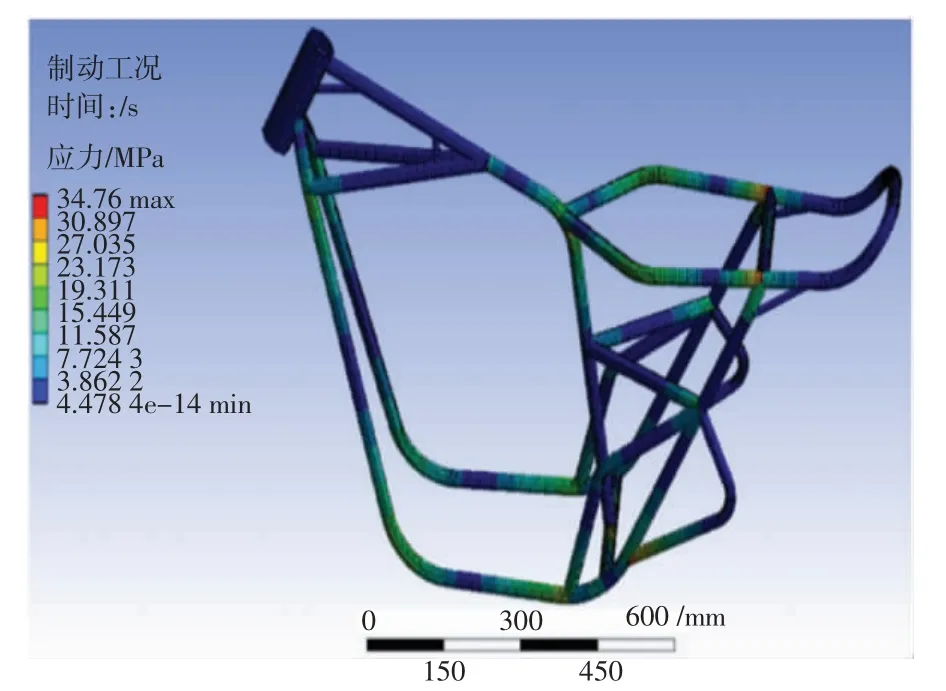
图8 车架制动工况应力云图
从图7 可以得出,车架最大位移出现在悬架支撑管的弯曲处,为0.35 mm。
从图8 可以得出,最大应力出现在上横管与边管连接处,为34.76 MPa。此处是多个管件连接处,会出现应力集中现象,并且车架整体突然受到向后的加速,容易产生较大的应力。与管件材料Q235 钢材的屈服极限235 MPa 相比,车架整体应力分布水平适中。
3.3.3 转弯工况
车架转弯工况是模拟电动摩托车在转弯时的情况。电动摩托车在紧急转弯时,车架会受到由离心力作用而产生的横向载荷,要求电动摩托车车架结构具有承受一定程度的横向载荷的能力。其中,离心加速度的大小由转弯时的车速和转弯半径决定,离心力的大小由车架的负载决定。车架在高速紧急转弯时将同时承受由离心力与弯曲载荷所产生的动载荷[7]。
转弯工况,需要在车架弯曲工况计算的基础上对车架加载1g 的横向加速度,并对车架进行如表4所示的边界约束。

表4 转弯工况车架边界约束条件
经过有限元分析与计算,该车架在转弯工况下的位移与应力云图分别如图9 与图10 所示。

图9 车架转弯工况位移云图

图10 车架转弯工况应力云图
从图9 可以得出,车架的最大位移出现在悬架支撑管的弯曲处,为0.27 mm。
从图10 可以得出,最大应力出现在上横管与边管连接处以及前管与下横管连接处,为35.96 MPa。由于车架整体突然受到横向加速,且这2 处为多个管件连接处,会出现应力集中现象,产生较大的应力。与管件材料Q235 钢材的屈服极限235 MPa 相比,车架整体应力分布水平适中。
3.3.4 碰撞工况
车架的碰撞工况是模拟电动摩托车在突发状况下正面撞上障碍物而被动停止的状况。本文建立了一个模型:假设电动摩托车以80 km/h 的速度在平直路面上匀速行驶,突然看到前方一辆轿车横穿马路,此时电动摩托车驾驶员紧急制动1 s 后与轿车侧身相撞,制动加速度取1.5g。经计算,电动摩托车与轿车侧身接触时车速为7.2 m/s,使轿车侧身产生0.3 m形变后减速至0 m/s,碰撞过程中的平均加速度可由以下公式求出:

式中:v=0;v0=7.2 m/s;x=0.3 m。
计算结果为a=-86.4 m/s2。
摩托车车架在碰撞工况还会受到来自轿车侧身的反作用力,反作用力可由以下公式求得:

式中:F 为轿车的反作用力,N;m 为电动摩托车总质量,为120 kg;a 为轿车侧身对摩托车施加的平均加速度,为-86.4 m/s2。
计算结果为F=10 368 N。
碰撞工况的边界约束条件与弯曲工况下的约束条件相同,但是需要在弯曲工况载荷分布的基础上对车架前端添加一个方向沿x 轴负方向、大小为10 368 N 的均布载荷以及一个同方向、大小为86.4 m/s2的加速度。
经过有限元分析与计算,车架在碰撞工况下的位移与应力云图分别如图11 与图12 所示。

图11 车架碰撞工况位移云图
从图11 可以得出,车架在碰撞工况下的最大位移出现在悬架支撑管的弯曲处,为2.15 mm。
从图12 可以得出,最大应力出现在支管与前撑管连接处以及前管与主管连接处,为180.45 MPa。由于多个管件连接处容易出现应力集中现象,且突然受到加速与正面载荷的作用,所以产生了较大的应力。车架整体应力分布水平稍高一些,但是与管件材料Q235 钢材的屈服极限235 MPa 还有一些距离,所以车架在碰撞工况下强度足够并且没有太多的冗余量。
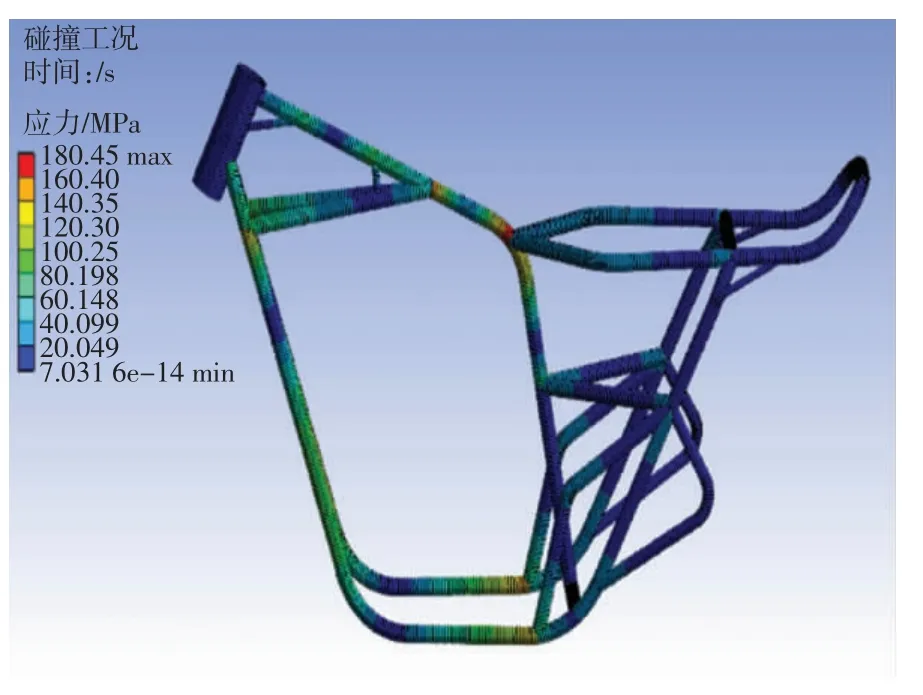
图12 车架碰撞工况应力云图
4 结论
本文基于CATIA 与ANSYS 软件,首先对电动摩托车车架进行了三维建模,再将模型导入ANSYS workbench 模块进行弯曲、制动、转弯、碰撞4 种工况的模拟与分析,得到了对应工况下的位移云图与应力云图。分析结果表明,车架的强度在材料许用范围内,且强度没有太多的冗余量。本文的分析结果为电动摩托车车架结构的设计与分析提供了理论指导,为提高电动摩托车的研发效率提供了参考。
