岩溶隧道涌突水破坏模式分类及防突厚度研究*
2022-05-11赵晓彦张巨峰
肖 喜 赵晓彦 张巨峰 肖 勇 莫 培
(①西南交通大学地球科学与环境工程学院,成都 611756,中国)(②中铁十九局集团第七有限公司,珠海 519000,中国)
0 引 言
我国是世界岩溶分布范围最广的国家,中西部地区岩溶广泛发育。据统计,可溶岩分布总面积约3.63×106km2,约占我国国土面积的1/3,尤其是云、贵、川、桂等部分地区最为发育(韩红艳等,2012)。
随着我国“十四五”规划的出台及交通强国战略的提出,隧道工程等基础设施建设将在地形陡峭、地质条件极端复杂的西南山区蓬勃发展,长大深埋隧道逐渐增多,施工过程中遇到的涌突水灾害造成隧洞失稳、地面沉降,严重影响施工进度、人员与设备的安全,制约工程建设(吴建等,2019)。在我国隧道建设过程中,“十隧九漏”说法由来已久,据统计约40%的隧道存在着不同程度的涌突水,而大型涌突水事件中,70%都发生在岩溶隧道中(康小兵等,2006)。如宜万线野三关隧道、怀邵衡铁路岩鹰鞍隧道、大张客专大梁山隧道涌突水造成了重大损失和工期严重延误(田四明等,2019)。造成突水事故频发的原因之一是没有将隧道与围岩之间防突岩体结构与防突岩体的破坏类型结合起来,造成防突厚度计算模型的不合理。
岩溶隧道涌突水破坏模式分类是研究涌突水灾害和计算防突厚度的基础,针对涌突水灾害分类和防突厚度计算,许多学者进行了大量的研究,取得了丰硕的成果。郭佳奇(2011)根据岩溶与隧道的位置关系将防突岩体简化为弹性梁模型、双孔洞模型、裂隙导通模型3种力学模型。杨子汉等(2017)根据溶洞的相对大小将防突岩体分为大跨度和中小跨度模型。陈帆(2018)根据防突层岩体的完整程度将其分为完整结构防突层、层状节理结构防突层、断续节理结构防突层、随机节理结构防突层。陈明庆(2019)将隧道涌突水破坏模式依据破坏类型划分为渗透型破坏、贯穿劈裂型破坏、综合型破坏3类并建立了突涌水灾害综合前兆信息判识体系。李利平等(2020)总结了常见的防突厚度计算模型并与实际的工程地质条件相结合,按照破坏模式将防突岩体防突层厚度计算分为适用于完整岩体和适用于裂隙岩体的两类计算公式。以上研究单独从防突岩体受力或者结构类型中的一方面进行分类,没有将两者结合起来考虑而存在局限性。
常见的防突厚度计算方法有经验公式法、洞顶坍塌法、坍塌平衡法、梁板受力模型法、剪切计算法等(李集等,2014)。赵明华等(2009)应用格里菲斯和库仑-莫尔判据计算出岩溶地区桩端下伏溶洞顶板稳定性并计算出最小厚度。莫阳春(2009)利用突变理论建立突水破坏计算模型,提出溶洞位于隧道顶部时的防突厚度计算公式。李利平等(2010a)认为隧道掌子面前方防突岩体由开挖引起的围岩松弛区、安全厚度区和裂隙带区3部分组成,并推导出隧道最小防突厚度的半解析解表达式。郭佳奇等(2017)把掌子面防突岩体视为弹性厚板,忽略岩溶水压力在掌子面高度上的差异,计算出简支和固支两种边界条件下的防突厚度计算公式。储汉东(2017)将防突层破坏模式分为整体破断失稳、水力劈裂破坏、关键块体失稳3种,并根据强度理论和突变理论分别求出防突岩体的安全厚度。郭佳奇等(2018)提出了隧道围岩为块状结构、溶洞位于掌子面前方、防突岩体发生翼形裂纹张拉贯通破坏时的防突厚度计算方法。吴祖松等(2020)把掌子面突水简化弹性薄板弯曲模型结合统一强度理论,假定掌子面受均布水压力作用下,推导出防突岩体分别在简支和固支条件下的掌子面防突厚度。
以往研究中,研究对象多针对于某一特定情况,研究的隧道围岩结构类型多为整体状岩体或裂隙岩体,尚未结合隧道围岩结构进行涌突水破坏模式的系统分类。本文以岩溶区隧道与周边隐伏溶洞间的防突岩体为研究对象,采用工程地质学、岩石力学、断裂力学、材料力学、弹性力学理论,研究隧道围岩的不同结构类型、溶洞位置及大小的涌突水破坏模式,并考虑岩溶水压力在掌子面高度上的差异的影响,建立岩溶隧道防突层各种破坏模式下防突厚度计算公式。研究结果对隧道选线和减少涌突水灾害具有实际工程应用价值。
1 岩溶隧道涌突水破坏模式分类
岩溶隧道涌突水破坏是隧道开挖空间与隐伏溶洞之间的岩体所形成的防突层在高水头岩溶水压力作用下的失稳破坏(贺振宇等,2017)。隧道围岩结构的不同,防突体发生突水失稳破坏的机理和过程就不同,所以计算岩溶隧道防突层突水破坏最小厚度必须要以防突层岩体结构为基础,再根据不同的破坏过程和机理确定防突厚度(李利平等,2010a)。
隧道围岩的结构类型可分为整体状结构、块状结构、层状结构、碎裂结构及散体状结构(谷德振,1979),根据隧道围岩类型,岩溶隧道涌突水破坏可分为对应的破坏模式。本文假定溶洞形状为椭球形,依据溶洞与隧道之间的相对位置不同,又可将突涌水破坏分为溶洞位于隧道上方、下方、侧方及掌子面前方4种。块状岩体主要是高压岩溶水在结构面中的水力劈裂作用,与溶洞的相对位置影响可忽略。因此,根据岩溶隧道的围岩类型、溶洞与隧道之间的相对位置关系,岩溶隧道涌突水破坏模式分成14大类,大类中根据溶洞与隧道的相对大小、溶洞沿隧道轴线长度b与隧道跨度a的比值、结构面的倾向及倾角大小,最后可细分为27小类,见表1。

表1 岩溶隧道涌突水破坏模式分类
2 岩溶隧道涌突水破坏防突厚度计算
2.1 隧道围岩为整体状结构的防突厚度计算
整体状结构是指防突层内不存在结构面或者只是存在对防突层的影响可以忽略的微结构面,隧道围岩为整体状结构时,防突层可发生拉破坏,剪切破坏或冲切破坏。根据溶洞的尺寸大小可将防突岩体简化为固支梁、固支板等模型。溶洞与隧道处于不同的相对位置,溶洞与隧道之间的防突岩体的自重对于防突厚度影响不同,水压方向与自重方向一致时,防突岩体最容易发生突水灾害。
2.1.1 溶洞位于隧道顶部
2.1.1.1 隧道顶部的Ⅰ型溶洞
溶洞位于隧道顶部且横跨隧道,即在隧道的横断面图上,溶洞在水平面上的投影包含隧道在水平面上的投影。当溶洞沿隧道底板轴向长度大于隧道开挖直径5倍时,防突岩体受力可简化为平面应变问题,即为隧道顶部的Ⅰ型溶洞(图1)。
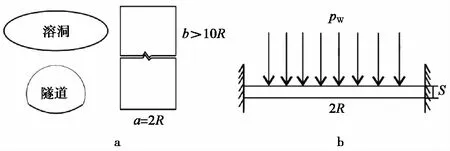
图1 整体状结构 溶洞位于隧道顶部的Ⅰ型溶洞
隐伏溶洞与跨度为a=2R的隧道间防突岩体上作用均布水压力PW,隐伏溶洞与隧道间的防突岩体为均质各向同性弹性体,忽略溶洞与隧道间防突岩体的成拱效应,溶洞与隧道间的防突岩体可简化为固支梁分析。固支梁在均布自重和岩溶水压力作用下,最大弯矩和最大剪力位置均位于梁的两端,最大弯矩M和最大剪力Q计算公式为:
(1)
(2)
按抗弯强度进行验算的防突厚度为:
(3)
按抗剪强度进行验算的防突厚度为:
(4)
S=max{S1,S2},取上述两式最大值作为防突厚度。

宜万线五爪观隧道里程DK48+871~DK49+960处发育该种类型溶洞,在溶洞为干溶洞情况下,郭佳奇(2011)计算防突厚度为4.27 m,按上述公式计算防突厚度约为1.8 m。
2.1.1.2 隧道顶部的Ⅱ型溶洞
溶洞位于隧道顶部且溶洞横跨隧道,即在隧道的横断面图上,溶洞在水平面上的投影包含隧道在水平面上的投影。溶洞沿隧道底板轴向长度小于等于隧道开挖直径5倍时,防突岩体可简化为一固支矩形板,即为隧道顶部的Ⅱ型溶洞(图2)。

图2 整体状结构 溶洞位于隧道顶部的Ⅱ型溶洞
隐伏溶洞与跨度为a=2R的隧道间的防突岩体上作用均布水压力PW,溶洞沿隧道轴线方向长度b=2L,以板的中心为坐标原点建立如图2b所示直角坐标系。溶洞与隧道间防突岩体为均质连续的各向同性弹性体,把防突岩体简化为受自重和均布水压力的边长为a、b的周边固定的等厚矩形薄板。徐芝纶(2006)利用伽辽金法求出固支矩形薄板挠度为:
(5)
(6)
根据弹性力学中应力与挠度的关系式可求出应力:
(7)
因剪应力τxy远远小于σx、σy,故没给出τxy表达式,带入化简取z=S/2可得在薄板长边中点处取得最大应力并满足如式(8)所示关系,因岩石的抗拉强度相比于抗压强度和抗剪强度最小,故用抗拉强度代替最大应力,即达到抗拉强度就发生破坏。
A1σtS2-B1γS-B1PW=0
(8)
(9)
(10)

宜万铁路沿线的大支坪隧道DKl37+768.5~DKl37+783.6范围内存在该种类型溶洞,张群(2019)计算防突厚度为5.64 m,通过上述公式计算防突厚度为6.19 m,结果比原文保守。
2.1.1.3 隧道顶部的Ⅲ型溶洞
当溶洞位于隧道顶部时,溶洞较小,溶洞整体或部分位于隧道正上方,即在隧道的横断面图上,隧道在水平面上的投影包含溶洞在水平面上的投影或溶洞在水平面上的投影与隧道在水平面上的投影相交。防突岩体可简化为冲切柱或剪切柱,即为隧道顶部的Ⅲ型溶洞(图3)。

图3 整体状结构 溶洞位于隧道顶部的Ⅲ型溶洞
溶洞位于隧道正上方时,防突体在高水头压力PW的作用下可在溶洞边缘处发生破坏,冲切剪切形成圆台冲切体或直接剪切形成圆柱剪切体。若溶洞不位于隧道正上方,溶洞与隧道之间所夹的防突岩体向隧道开挖面直接剪切破坏。
直接剪切破坏时,均布水压力PW作用于防突岩体顶部,同时受自身重力W,侧面切应力τ提供抗力,假定剪切面上应力均匀分布,灰岩的破坏判据符合强度包络线为双曲线型的莫尔强度判据(刘佑荣,2009)。赵明华等(2009)运用格里菲斯强度判据及第三强度理论,并考虑安全系数计算出岩溶区桩端下伏溶洞顶板直接剪切破坏最小安全厚度为:
(11)
式中:σ为该处水平地应力(kPa);Q为桩端荷载(kN);d为桩端直径(m);这里将溶洞水压力PW类比于桩端荷载,同时考虑防突岩体重力作用,σ如果没有实测资料则取σ=0,可计算防突厚度为:

(12)
(13)
冲切破坏时,防突岩体在水压PW的作用下形成圆台形冲切体。破坏的圆台顶面半径为R,假定冲切面上的应力为均匀分布,赵明华等(2009)运用格里菲斯强度判据计算出岩溶区桩端下伏溶洞顶板最小安全厚度为:
(14)
(15)
式中:Q为桩端荷载,这里将溶洞水压力PW类比于桩端荷载,同时考虑防突岩体重力作用,为了计算公式简洁将圆台形冲切体简化为圆柱体计算其自重。可计算防突厚度为:
(16)
可得A2S2+B2S+C2=0
则计算防突厚度为:
(17)
其中:
(18)
S=max{S1,S2},上述两式最大值作为防突厚度。
式中:θ为冲切角(°);φ0为防突岩体内摩擦角(°);σc为岩石单轴抗压强度(kPa);σt为岩石的抗拉强度(kPa);σ为岩层中天然水平应力(kPa);如果没有相关数据可取值为0;W为冲切破坏的圆台或直接剪切破坏圆柱的重力(kN);R1直接剪切破坏的圆柱体半径或冲切破坏的圆台上底面半径(m)。
宜万铁路沿线的大支坪隧道DKl37+768.5~+783.6内存在一水压充填溶洞,也可看成该类型,则只会发生直接剪切破坏,郭佳奇(2011)计算防突厚度为4.27 m,按上述公式计算为6.26 m,与简化为薄板型的防突厚度比较接近。
2.1.2 溶洞位于隧道底部
2.1.2.1 隧道底部的Ⅰ型溶洞
溶洞位于隧道底部且横跨隧道,即在隧道的横断面图上,溶洞在水平面上的投影包含隧道在水平面上的投影。当溶洞沿隧道底板轴向长度大于隧道开挖直径5倍,防突岩体受力可简化为平面应变问题,即为隧道底部的Ⅰ型溶洞。
与溶洞位于隧道顶部的Ⅰ型类似,但此处重力方向与水压力方向相反,最大弯矩位置最大剪力位置均出现在梁的两端。根据溶洞位于隧道顶部计算公式,同理可得按照抗弯与抗剪强度计算出防突厚度。
按抗弯强度进行验算的防突厚度为:
(19)
按抗剪强度进行验算的防突厚度为:
(20)
S=max{S1,S2},取上述两式最大值作为防突厚度。
鲁竹坝二号(Ⅱ线)隧道在DK205+030~DK205+210区段遇到的溶腔主要位于隧道底部,可看作此种类型。郭佳奇(2011)计算防突厚度为4.85 m,按上述公式计算防突厚度为0 m。
2.1.2.2 隧道底部的Ⅱ型溶洞
溶洞位于隧道底部,溶洞横跨隧道,即在隧道的横断面图上,溶洞在水平面上的投影包含隧道在水平面上的投影。当溶洞沿隧道底板轴向长度小于等于隧道开挖直径的5倍,防突岩体可简化为一固支矩形薄板,即为隧道底部的Ⅱ型溶洞。与位于隧道顶部Ⅱ型溶洞类似,但此处重力方向与水压力方向相反,同理可求得防突厚度为:
(21)
与整体状结构,溶洞位于隧道顶部的Ⅱ型溶洞类似,此处不举例。
2.1.2.3 隧道底部的Ⅲ型溶洞
当溶洞位于隧道底部时,溶洞较小,溶洞整体或部分位于隧道正上方,即在隧道的横断面图上,溶洞在水平面上的投影包含隧道在水平面上的投影或溶洞在水平面上的投影与隧道在水平面上的投影相交。防突岩体可简化为冲切柱或剪切柱,即为隧道底部的Ⅲ型溶洞。
与溶洞位于隧道顶部的Ⅲ型溶洞对比,此处水压力与防突层自身重力方向相反,此种类型溶洞与隧道间的防突岩体突水破坏主要有直接剪切破坏和冲切破坏两种类型。
直接剪切验算防突层厚度为:

(22)
按冲切剪切验算得防突层厚度:
(23)
则计算防突厚度为:
(24)
式中:
(25)
S=max{S1,S2},取上述两式最大值作为防突厚度。
与整体状结构且溶洞位于隧道顶部的Ⅲ型溶洞类似,此处不举例。
2.1.3 溶洞位于隧道侧部
2.1.3.1 隧道侧部的Ⅰ型溶洞
溶洞位于隧道侧部时且洞顶高于隧顶、洞底低于隧底,即在隧道的横断面图上,溶洞在竖直平面上的投影包含隧道在竖直面上的投影。且溶洞沿隧道底板轴向长度大于隧道开挖直径5倍,防突体可简化为固支梁,即为隧道侧部的Ⅰ型溶洞(图4)。

图4 整体状结构 溶洞位于隧道侧部的Ⅰ型溶洞
固支梁一侧承受呈梯形分布的岩溶水压力作用,可将梯形荷载分均布荷载p0和三角形荷载p1两部分分别进行计算,然后根据叠加原理,将两者计算的弯矩和剪力叠加,得梯形荷载作用下防突体的最大弯矩和最大剪力,张军伟等(2017)按抗弯与抗剪强度求得防突厚度。
按抗弯强度进行验算的防突厚度为:
(26)
按抗剪强度进行验算的防突厚度为:
(27)

宜万线大支坪隧道 Ⅰ 线左侧DK132+960~DK132+980段发育大型富水充填溶洞,可视为该种类型,曾艺(2015)用该公式计算防突厚度为4.79 m。
2.1.3.2 隧道侧部的Ⅱ型溶洞
溶洞位于隧道侧部且洞顶高于隧顶、洞底低于隧底,即在隧道的横断面图上,溶洞在竖直平面上的投影包含隧道在竖直面上的投影。且溶洞沿隧道底板轴向长度b小于等于隧道开挖直径a的5倍,防突岩体受力可简化为受线性荷载的固支矩形薄板,即为隧道侧部的Ⅱ型溶洞(图5)。

图5 整体状结构 溶洞位于隧道侧部的Ⅱ型溶洞力学模型
按图5所示建立直角坐标系,在岩溶水压力作用下,该防突岩体可以简化为边长为a、b的受线性荷载的周边固支矩形薄板模型,岩溶水压力可以分解为两部分,一部分是薄板顶部的均布水压力p0,另一部分是静水压力p1。孙建等(2015)求得均布载荷作用下四边固支矩形薄板应力表达式为:
(28)
(29)

根据叠加原理,将上述式子对应相加可得相应应力表达式,在(2R,L)处取得最大应力为:
(30)
因为岩石的抗拉强度相比于抗压强度和抗剪强度最小,用岩石抗拉强度σt代替σmax,根据第一强度理论,即达到抗拉强度就发生破坏,求出防突厚度S:
(31)
其中:A22=DA11;B22=DB11
式中:a为隧道的开挖高度(m);b为溶洞沿隧道底板轴向长度(m);其他符号同上。
忠垫高速公路某隧道YK5+868.5~YK6+883.6里程内存在一充满岩溶水的该类型溶洞,郭佳奇等(2010)计算防突厚度为4.02 m,按上述公式计算防突厚度为4.75 m,计算结果比原文保守。
2.1.3.3 隧道侧部的Ⅲ型溶洞
溶洞位于隧道侧部时且溶洞较小,溶洞整体或部分位于隧道侧部。即在隧道的横断面图上,溶洞在竖直面上的投影包含隧道在竖直面上的投影或溶洞在竖直面上的投影与隧道在竖直面上的投影相交。防突岩体可简化为冲切柱或剪切柱,即为隧道侧部的Ⅲ型溶洞(图6)。

图6 整体状结构 溶洞位于隧道侧部的Ⅲ型溶洞
与前两种Ⅲ型溶洞对比,此种类型忽略重力对防突厚度的影响,溶洞与隧道间的防突岩体突水破坏主要有直接剪切破坏和冲切破坏两种类型。
直接剪切验算防突层厚度为:
(32)
按冲切剪切验算得防突层厚度为:
(33)
S=max{S1,S2},取上述两式最大值作为防突厚度。
某岩溶隧道正洞DKl909+345.2处两侧拱脚钻孔,孔深达到3.8 m时,出现喷射涌水,涌突水破坏类型可看作此类,郭佳奇(2011)将之视为裂隙岩体计算防突厚度为3.41 m,按上述公式计算防突厚度约为1.74 m,原文计算太过保守。
2.1.4 溶洞位于掌子面前方
2.1.4.1 隧道掌子面前方的Ⅰ型溶洞
当溶洞位于隧道掌子面前方时,溶洞跨过隧道,即在隧道的横断面图上,溶洞在竖直平面上的投影包含隧道在竖直面上的投影。即为隧道掌子面前方的Ⅰ型溶洞(图7)。

图7 整体状结构 溶洞位于掌子面前的Ⅰ型溶洞
在岩溶水压力作用下,该防突岩体可以简化为受线性荷载的周边固支圆板薄板模型,水压力可以分解为两部分,是与圆板中心处集度的均布水压力p0,另一部分是反对称水压力p1。徐芝伦(2006)根据平衡、几何和物理方程建立挠度微分方程,结合边界条件计算出均布荷载p0的径向弯矩Mr和环向弯矩Mθ解答为:
(34)
最大弯矩在圆板的边缘处:
(35)
吴家龙(2016)计算出反对称荷载p1的解答:
(36)
最大弯矩在圆板的边缘处θ=0或θ=π处:
(37)
根据叠加原理,圆板所受最大弯矩为:
(38)
防突岩体最先破坏位置为掌子面底部拉破坏。根据弯矩与应力的关系:
(39)
取z=S/2,σr达到最大值,达到抗拉强度就发生破坏,可求得防突厚度S为:
(40)

云雾山隧道Ⅱ线进口处遭遇IIDK245+526溶腔可视为该类型溶洞,张群(2019)计算防突厚度为3.67 m,利用上述公式计算得4.84 m。
2.1.4.2 隧道掌子面前方的Ⅱ型溶洞
溶洞位于隧道掌子面前方时,溶洞较小,溶洞整体或部分位于隧道掌子面前方,溶洞在竖直面上的投影包含隧道在水平面上的投影,即为隧道掌子面前方的Ⅱ型溶洞。
由于位于隧道掌子面前方的Ⅱ型溶洞与位于隧道侧部的Ⅲ型溶洞的破坏模式相同,所以隧道掌子面前方的Ⅱ型溶洞防突厚度计算方法与位于隧道侧部的Ⅲ型溶洞计算方法相同,见式(32)与式(33)。
2.2 隧道围岩为块状结构的防突厚度计算公式
在实际工程建设中所面对的隧道与溶洞之间的岩体为整体状结构是不太常见的,更多的防突体结构类型是一种包含短小、断续节理的相比于整体状结构更加复杂的块状结构类型。研究这类防突层的岩体结构类型涌突水破坏具有重要意义。
在断裂力学中根据断续节理面上法向应力状态是拉应力或压应力把块状结构防突层破坏分为拉剪破坏或压剪破坏两种模式。郭佳奇等(2012)认为,地下岩体中裂纹发生拉剪破坏模式的临界水压力远大于发生压剪水力破坏模式的临界水压力。因此自然情况下裂隙岩体的水力劈裂为压剪破坏模式。
在高水头压力作用下,防突岩体中的裂纹开始扩展。块状岩体在高水压力条件下的破坏起裂点和破坏特征与裂纹的产状及其与最大主压应力方向夹角大小有关(赵海军等,2019)。两条裂纹不重叠且中间岩桥倾角较大时,岩桥区域的接触力集中程度增大,岩桥区域首先出现竖向的微张拉裂纹并演化竖向的宏观裂纹连接两个预制裂隙端点(王志文等,2019;张晗等,2021)。研究表明,岩石压剪破坏裂纹的贯通破坏模式有翼形裂纹张拉贯通破坏、拉剪复合断裂破坏(刘涛影等,2012)。
块状断续节理岩体受地应力σ1,σ3作用,长度为2a的断续裂纹内孔隙水压力为pW,裂纹与方向为竖直方向的最大主应力σ1之间的夹角为ψ,假定水压力沿裂纹各个方向作用力相等。裂纹间的垂直距离为D,h为相邻上下两条裂纹相邻端部间沿裂纹走向的距离(图8)。裂纹面上的正应力σn和剪应力τn(这里以压为正)表示为:

图8 块状结构中断续节理分布图及力学模型
(41)
2.2.1 翼形裂纹张拉贯通破坏
当裂纹断裂强度因子KⅠ大于断裂韧度值KⅠC,裂纹开始扩展(图9),翼型初始裂纹将沿周向最大正应力方向扩展,开裂角θ=70.5°(程靳等,2020)。EF、AB分别为上、下裂纹的一半。当外荷载不断增加,岩体中首先出现翼形裂纹,同时产生张拉裂纹CD,然后张拉裂纹CD和BC、DE连通。张拉裂纹CD沿着最大压应力方向扩展,为了计算简便,这里将翼型裂纹简化为沿最大主应力σ1方向的直线。裂纹CD表面的法向应力达到岩体的抗拉强度σt,裂纹开始贯通(杨慧,2010)。

图9 翼形裂纹张拉贯通破坏分析图及示意图
郭佳奇等(2018)根据翼型支裂纹扩展至临界长度的尖端应力强度因子等于岩石的断裂韧度为破坏突水的判据,即KⅠC=KⅠw(lc),lc=D/(2sinψ)。计算出断续节理岩体发生翼型裂纹张拉贯通破坏的防突厚度S为:
(42)

宜万铁路线云雾山隧道DK245+526~DK245+547段一溶洞可视为该类型,施工现场预留岩墙厚度3.24 m(舒佳军等,2021),根据上述公式并考虑扰动带厚度(一般取1.5 m)计算防突厚度为3 m。
2.2.2 拉剪复合断裂破坏
尖端起裂后,裂隙尖端B、E分别将产生翼形裂纹BC与DE。而岩桥间抗剪能力不断被削弱,当翼形裂纹扩展到了一定程度时,其尖端C、D两点被剪切应力所贯穿,从而造成剪切方向裂纹汇合贯通(图10),岩体剪切破坏(杨慧,2010)。

图10 拉剪复合断裂破坏破坏分析图及示意图
EF、AB分别为断续节理裂纹的上、下裂纹之半,长度均为a;CD为裂纹间的岩桥;θ为岩桥与竖直方向的夹角;σCD和τCD为岩桥上的正应力和剪应力;BC和DE是由裂纹AB和EF的剪切应力造成的翼形分支裂纹。根据力的平衡条件,可得:
(43)
得岩桥上正应力和剪应力为:
(44)
其中:
根据Mohr-Coulomb强度准则及防突层岩体的侧压力系数λx与水力劈裂带到掌子面的距离Sx关系(郭佳奇等,2018)
(45)
再联立式(46)及σ3=λσ1,即可求出岩桥发生拉剪复合断裂破坏防突厚度S为:
(46)
式中:θ为岩桥与竖直方向夹角(°);PW为水压力(kPa);c为岩桥的黏聚力(kPa);φ为岩石的内摩擦角(°);其他符号同上。
宜万铁路线云雾山隧道DK245+526~DK245+547段一溶洞若用上述公式计算,结果为负值,该溶洞不会发生拉剪复合断裂破坏。
2.3 隧道围岩为层状结构的防突厚度计算公式
岩体的破坏,总是沿着软弱结构面破坏,层状结构岩体的层面为软弱结构面,故层状结构岩体涌突水失稳破坏主要有两种,当层面倾角较大,沿结构面的顺层剪切破坏;当层面倾角较小无法发生顺层剪切破坏,此时岩层近于水平,层面不再是发生失稳的破坏面,层状结构岩体涌突水破坏类似于整体状岩体涌突水破坏。
2.3.1 溶洞位于隧道顶部
由于结构面向左侧倾与向右侧倾完全对称,计算方法相同。在此以结构面左侧倾为例分析计算。α为同时与溶洞右边缘和隧道左边缘相切直线与水平方向所形成的夹角,f为结构面的摩擦系数,β=max{α,arctanf}
2.3.1.1 溶洞位于隧道顶部且结构面倾角大于β
防突岩体层状结构,结构面倾角为θ。当x方向达到极限平衡状态时(式(47)),防突岩体发生沿层面剪切贯通破坏,层面和两边完整岩体提供抗剪强度(图11)。此时的破坏岩体是以溶洞或隧道较小尺寸为宽、溶洞沿隧道轴线的尺寸为长,以防突体厚度为高的斜棱柱。重力与水压方向相同,重力为涌突水破坏的动力,容易发生涌突水灾害。

图11 层状结构 溶洞位于隧道顶部且结构面倾角大于β
PW2Rbsinθ+2RbγSsinθ=2cscθτ1Sb+2τ2S2R
(47)
可得:
(48)
其中:τ1=Cj+k∑γiHisinθtanφj
τ2=Cm+k∑γiHitanφm

重庆东泉隧道掌子面里程DK103+627处,现场开挖揭示,拱部垂直于隧底方向发育有一约6.3 m×4.2 m×3.6 m(环向×纵向×径向)岩溶溶洞。掌子面围岩为弱风化岩溶角砾岩夹层状灰岩,岩层倾向于线路右侧,可视为该类型,由于没有相关地应力资料,相关参数按经验取值,在2 MPa水压力下,计算防突厚度为3.52 m。
2.3.1.2 溶洞位于隧道顶部且结构面倾角小于β
岩层近乎水平,不会发生顺层剪切破坏,此时发生涌突水破坏模式与整体状结构岩体类似,可能为拉破坏或剪切破坏,按溶洞大小分为Ⅰ、Ⅱ、Ⅲ型溶洞,可参照隧道围岩为整体状岩体计算防突厚度。见式(3)、式(4)、式(9)、式(12)、式(17),然而层状岩体与整体状岩体还是有差别,可根据经验乘相应的系数。
2.3.2 溶洞位于隧道底部
由于结构面向左倾与向右倾完全对称,此处以结构面左倾为例分析计算。α为同时与溶洞左边缘和隧道右边缘相切直线与水平方向所形成的夹角,f为结构面的摩擦系数,β=max{α,arctanf}。
2.3.2.1 溶洞位于隧道底部且结构面倾角大于β
与溶洞位于隧道顶部且结构面倾角大于β类似,重力与水压方向相反,重力为涌突水破坏的抗力不容易发生涌突水灾害(图12),防突厚度相较于同种情况但溶洞位于隧道顶部时小,计算防突厚度为:

图12 层状结构 溶洞位于隧道底部隧道顶部且结构面倾角大于β
(49)
重庆东泉隧道掌子面里程DK103+627处,掌子面围岩为弱风化岩溶角砾岩夹层状灰岩,岩层倾向于线路右侧,若溶洞位于隧道底部,则可视为该类型,在2 MPa水压力下,计算防突厚度为3.23 m。
2.3.2.2 溶洞位于隧道底部且结构面倾角小于β
岩层近于水平,不会发生顺层剪切破坏,此时发生涌突水破坏模式与整体状结构岩体类似,可能为拉破坏或剪切破坏,按溶洞大小分为Ⅰ、Ⅱ、Ⅲ型溶洞,可参照隧道围岩为整体状岩体计算防突厚度。见式(19)、式(20)、式(21)、式(22)、式(24),然后可根据经验乘相应的系数。
2.3.3 溶洞位于隧道侧部2.3.3.1 溶洞位于隧道侧部且结构面倾向隧道
防突岩体结构面倾向隧道,倾角为θ。重力有沿结构面向下的分量,重力为涌突水破坏的抗力。此时PW为防突体中心的水压力,即作用于防突上的平均水压力。当x方向达到极限平衡状态时,发生剪切贯通破坏时(图13)。层面和两侧岩体提供抗剪强度,此时的破坏岩体亦呈斜棱柱状。计算防突厚度为:

图13 层状结构 溶洞位于隧道侧部且结构面倾向隧道
(50)

图14 层状结构溶洞位于隧道侧部且结构面倾向溶洞
当结构面水平时,上式中,θ=0,即可求出结构面水平时的防突厚度。
重庆东泉隧道掌子面里程DK101+662处,掌子面围岩为弱风化灰岩,岩层为水平状,层间局部夹泥。左侧边墙发育一处岩溶溶腔,可视为该类型,若在2 MPa水压下,计算防突厚度约为3.31 m。
2.3.3.2 溶洞位于隧道侧部且结构面倾向溶洞
与防突岩体结构面倾向隧道类似,这里PW为防突体中心的水压力,发生剪切贯通破坏时重力有沿结构面向下的分量,重力为涌突水破坏的动力。防突岩体沿层面破坏,计算防突厚度为:
(51)
重庆东泉隧道掌子面里程为DK101+662处溶洞也可用该公式计算,得出相同结果。
2.3.3.3 溶洞位于隧道侧部且结构面竖直
此种模式不会发生压剪断裂破坏,破坏模式与整体状结构岩体类似,可能为拉破坏或剪切破坏,按溶洞大小分为Ⅰ、Ⅱ、Ⅲ型溶洞,参照隧道围岩为整体状岩体计算防突厚度。见式(26)、式(27)、式(31)、式(32)、式(33),再根据经验乘相应的系数。
2.3.4 溶洞位于掌子面前方
2.3.4.1 溶洞位于掌子面前方且结构面倾向隧道
溶洞位于掌子面前方且结构面倾向隧道同溶洞位于隧道侧部且结构面倾向隧道的防突厚度计算模型与计算方法完全相同。此时式(50)中b不是代表溶洞沿隧道轴线方向的长度而是代表溶洞直径或隧道直径中的较小值。
2.3.4.2 溶洞位于掌子面前方且结构面倾向溶洞
溶洞位于掌子面前方且结构面倾向溶洞同溶洞位于隧道侧部且结构面倾向溶洞防突厚度计算模型与计算方法完全相同。此时式(51)中b代表溶洞直径或隧道直径中的较小值。
2.3.4.3 溶洞位于掌子面前方且结构面竖直
此种模式不会发生压剪断裂破坏,发生涌突水破坏模式与整体状结构岩体类似,可能为拉破坏或剪切破坏,按溶洞大小分为Ⅰ与Ⅱ型溶洞,可参照隧道围岩为整体状岩体计算防突厚度。见式(32)、式(33)、式(40),再根据经验乘相应的系数。
2.4 隧道围岩为碎裂结构及散体状结构的防突厚度计算公式
防突岩体结构为碎裂结构及散体状结构时,可视作连续均匀介质,且具有良好的渗透性。溶洞与隧道相对大小不会造成破坏模式的改变,都沿隧道与溶洞之间最小距离方向发生直接剪切破坏。
2.4.1 溶洞位于隧道顶部
防突岩体破坏体是以溶洞或隧道中的较小尺寸为宽、溶洞沿隧道轴线的尺寸为长,防突体厚度为高的斜棱柱,此处的重力为涌突水破坏的动力,同时考虑动水压力GD对防突厚度的影响(图15)。根据∑Fx=0,

图15 碎裂结构及散体状结构 溶洞位于隧道顶部
PW2Rbsinθ+2RbSγsinθ+2RbSiγw
=2(2R+b)(Cm+k∑γiHitanφm)
(52)
可计算防突厚度为:
S=
(53)

祁连山隧道DK337+320~DK337+450通过F7断层,可视为该类型,孟凡树等(2020)不考虑开挖扰动的防突厚度为8.16 m,本文根据上述公式计算防突厚度约为7.24 m。
2.4.2 溶洞位于隧道底部
同溶洞位于隧道顶部计算方法,但此时重力为涌突水破坏的抗力,溶洞位于隧道底部防突厚度为:
S=
(54)
与溶洞位于隧道底部相似,此处不举例。
2.4.3 溶洞位于隧道侧部
同溶洞位于隧道顶部计算方法,此时PW为防突体中心处的水压力,此处不考虑防突体重力对防突厚度的影响,溶洞位于隧道侧部防突厚度为:
(55)
东泉隧道里程DK101+645处右侧综合洞室,埋深约51 m。围岩为弱风化灰岩,岩层夹泥,节理裂隙发育,岩体较破碎,稳定性差,拱顶易掉块,揭示一溶腔,可视为该类型,假设在水压2 MPa作用下,根据上述公式计算防突厚度为约4 m。
2.4.4 溶洞位于掌子面前方
同溶洞位于隧道侧部防突厚度计算,但此时的防突岩体破坏体是以溶洞与隧道尺寸的较小值为直径的圆柱体,PW为防突体破坏体中心的水压力,溶洞位于掌子面前方防突厚度为:
(56)
钟家山隧道F2断层破碎带,当距离F2断层带约5.2 m处,掌子面出现湿化、软化并伴有淋水的现象,若继续开挖将可能发生涌突水破坏,陈泽龙(2020)取防突厚度为5.2 m。该处涌突水破坏可看作此类型,计算防突厚度约为4.2 m。
本文计算的防突厚度是根据力学原理计算出的极限状态下防突厚度,工程实践可根据实际情况增加该厚度进行相关设计。
3 结 论
(1)将隧道围岩类型与溶洞和隧道之间的相对位置关系相结合,划分出14种涌突水破坏类型。系统总结得出各破坏类型的防突厚度计算公式。工程实践可根据实际情况增加该计算厚度进行相关设计。
(2)隧道围岩为整体状结构时,隧道顶、底、侧部溶洞可简化为梁模型、矩形薄板模型、冲剪切柱模型等,防突厚度计算准则分别为第一强度理论、第三强度理论、格里菲斯判据。计算出溶洞位于掌子面前方受线性荷载水压力的防突厚度精确解。
(3)块状结构的隧道围岩涌突水破坏有翼形裂纹张拉贯通破坏和拉剪复合断裂破坏两种破坏模式,防突厚度表达式与溶洞大小及溶洞和隧道之间的相对位置无关。节理裂隙长度及间距、与最大主应力夹角都影响两种破坏模式的防突厚度大小。
(4)层状结构的隧道围岩涌突水破坏,若层面倾角较大时主要沿层面剪切破坏,防突厚度计算与溶洞的相对大小无关,与结构面的倾角及倾向有关;若层面倾角较小按相应类型的完整岩体考虑。
(5)隧道围岩为碎裂结构及散体状结构,防突体发生剪切破坏,该类岩体结构渗透系数大,隧道开挖时渗流明显,防突厚度计算应充分考虑动水压力影响。
