MTS试验机岩石压缩试验变形测量数据的选取方法研究*

2022-05-11靳一鼎徐荣超李日运王四巍袁广祥李洪军

工程地质学报 2022年2期

靳一鼎徐荣超李日运王四巍袁广祥李洪军

(①华北水利水电大学地球科学与工程学院，郑州 450046，中国)(②中国电建集团北京勘测设计研究院有限公司，北京 100024，中国)

0 引言

岩石试验是岩石力学的基础，是研究岩石力学与工程的重要手段之一(杨更社等，2001)。为了解岩石的基本力学性质、获取其力学参数，首先应当对岩石进行力学强度试验。其中，岩石的抗压强度是岩体稳定性分析的重要力学参数，单轴和三轴压缩试验是获取岩石抗压强度的主要方法，此外通过分析试验得到的应力-应变曲线可以获取其他描述岩石强度及变形特性的参数，如弹性模量、泊松比、应力门槛值等。国际岩石力学和岩石工程学会(ISRM)在1979年和1983年对岩石单轴和三轴压缩试验提出了详细的测试方法(Bieniawski et al.，1979；Kovari et al.，1983)。随着自动化和电液伺服技术的成熟和广泛应用，运用伺服控制方式进行加载和电子计算机进行实时数据采集已经成为岩石力学室内试验的主要手段(唐海燕等，2004；汪斌等，2010)。目前，MTS815型电液伺服岩石力学试验系统成为国内外各大高校及科研院所岩石力学室内试验使用较多的仪器设备，主要用于测试岩样在不同应力条件下的力学性质。该系统具有整体刚度高、测试精度高、性能稳定等优点，此外还具备加载控制方式多样化的特点，如采用轴向力、轴向变形、径向变形等控制方式。侯振坤等(2015)、陈国庆等(2018)、王传乐等(2018)和杜瑞锋等(2019)均使用MTS815试验机进行岩石的单轴压缩、三轴压缩等各项试验。

在岩石的单轴、三轴压缩试验中，采用不同加载控制方式得到的岩石应力-应变曲线形态不同。根据曲线的形态把应力-应变曲线分为Ⅰ类和Ⅱ类两种曲线(Wawersik et al.，1970)(图1)。通常而言，加载控制方式为轴向应变控制时，得到的应力-应变曲线在应变上是单调递增的，即Ⅰ类曲线。然而，当岩石脆性较高时，在轴向应变加载方式控制下，岩样易在达到峰值强度后发生突然破坏，无法得到完整峰后曲线。但采用其他加载控制方式(Lockner et al.，1991；Fairhurst et al.，1999)获得的Ⅱ类曲线，试样不会出现突然破坏的现象。一些学者对此进行研究，陈绍杰等(2010)发现Ⅱ类曲线本质上是脆性岩石试件在压缩破坏时的卸载过程中得到的，它的产生是有条件的。Wong et al.(2019)对Ⅱ类曲线的发生机理及影响因素进行了研究，认为Ⅱ类曲线的形状取决于峰前阶段弹性能与耗散能的比例，及峰后阶段塑性变形或新裂纹的萌生和扩展所消耗的能量，并提出了将径向应变作为控制变量来指导轴向荷载的施加以获得完整的应力-应变曲线。

图1 岩石单轴压缩应力-应变曲线

采用MTS试验机完成单轴压缩试验和三轴压缩试验后，需要获取并计算试验数据来得到完整的应力-应变曲线。为了得到更为准确的应力-应变曲线，采用不同测量装置对试样在试验中的变形进行测量。目前变形测量数据的获取有3种途径：LVDT、引伸计、压板位移。不同测量方法获得的试验数据不同，试验研究者通常直接采用引伸计获得的变形测量数据进行应力-应变曲线的绘制、应力门槛值的分析和变形参数的计算，如：钟志彬等(2017)。然而引伸计获得的变形数据能否代表岩石真实的变形特性需要开展深入分析，目前国内外已有文献中未见此方面的报道。

本文采用MTS试验机进行岩石的单轴和三轴压缩试验，系统分析压板位移、LVDT、引伸计3种轴向变形测量方法得到的变形数据，对试样应力-应变曲线形态进行研究分析。同时，对不同测量方法下试样的应力门槛值(起裂强度σci、损伤强度σcd)及变形参数(弹性模量E、泊松比ν)的准确性和适用性进行探讨。最后提出对MTS试验机岩石压缩试验变形数据选取的建议。

1 试验设备与试验方法

1.1 试验设备

本试验采用MTS815.04电液伺服岩石力学试验系统进行单轴和三轴压缩试验。MTS试验机(图2)可操控的控制方式包括：轴向力控制、轴向位移控制、内置力传感器力控制、轴向引伸计位移控制、径向引伸计位移控制等。

图2 MTS815三轴试验机

1.2 变形测量

MTS试验系统对岩样轴向变形测量采用的装置是引伸计(图3)，引伸计测量范围为50imm，安装在试样中部。即在试验过程中，采集岩样中部50imm范围内的轴向变形，之后再除以标距得到轴向应变值。所以，通过引伸计测量得到的轴向应变值并不包括标距外试样两个端部的变形，严格讲只是岩样中间部分(50imm)的轴向应变，而非整个试件的轴向变形。

图3 安装轴向引伸计的岩石试样

径向变形的测量采用链式引伸计，其原理是用一个内置应变规的插头将围裹试件的链条两端卡紧，试件膨胀或收缩会引起应变规电路两端电压线性变化，以此来量测试件直径的变化量(唐海燕等，2004)。

1.3 压缩试验方案

单轴压缩试验采用的岩石试样为大理岩、花岗岩和玄武岩。按照国际岩石力学学会(ISRM)《岩石力学试验建议方法》(1982)制备标准试件尺寸为φ50imm×100imm圆柱形试样，直径和高度偏差小于0.2 mm，上下端面平整度误差小于0.05 mm。试验采用轴向位移的控制方式，其加载速率为0.001 mm·s-1，实时记录岩样的轴向载荷、轴向位移和径向位移。

三轴压缩试验所采用的页岩取自川渝地区志留系龙马溪组。试样制备规格同上文大理岩。为了得到页岩的全应力-应变曲线，试验中先施加围压，以3iMPa·min-1的速率加载到30iMPa；等围压稳后，再施加轴向应力，加载方式采用先以30ikN·min-1的速率加载至50ikN左右，再改为径向位移控制，并以0.04 mm·min-1的速率继续加载，目的是为了得到完整的峰后曲线。尹晓萌等(2017)在进行三轴压缩试验中也采用这种加载控制方法。需要说明的是，本文三轴压缩试验的数据来源于四川大学何柏等(2017)，所以本文三轴压缩试验的加载速率与单轴压缩试验的加载速率不同。

2 结果与分析

2.1 应力-应变曲线峰值前数据分析

根据轴向引伸计和压板位移测量得到的变形数据计算出岩样的轴向应变，绘制大理岩在轴向位移控制下单轴压缩试验的全应力-应变曲线(图4)。其中，压板位移测量的方式为压头的轴向变形量除以整个岩样的高度。从图4中可以清楚看到，在峰前阶段相同轴向应力下压板位移测量得出的轴向应变明显大于引伸计测量得出的轴向应变，特别体现在两条曲线峰值前的斜率上。经过分析发现，试验中采用压板位移的方法进行变形测量时，记录的位移值不仅包含岩样的变形位移，同时将压头和垫块在轴向压力作用下的位移变形量及两者之间接触缝隙的位移量计算在内，最终由压板位移计算得出的轴向应变与岩样实际的轴向应变相比要大一些。

图4 大理岩轴向引伸计和压板位移应力-应变曲线的比较

为了分析其他岩性的岩石在压缩试验下应力-应变曲线是否存在同样的现象，进一步对花岗岩和玄武岩进行试验研究。图5和图6分别表示为花岗岩和玄武岩在轴向位移控制下单轴压缩试验的全应力-应变曲线。由图5和图6可见，无论是花岗岩还是玄武岩，在峰前阶段相同轴向应力下压板位移测量得出的轴向应变均明显大于引伸计测量得出的轴向应变，这与大理岩在单轴压缩试验下出现的情况相同。说明岩性并不会对引伸计和压板位移测量得到的结果造成其他偏差，不同岩性的岩石在单轴压缩试验下压板位移测量得到的轴向应变都要比岩样实际的轴向应变要大。

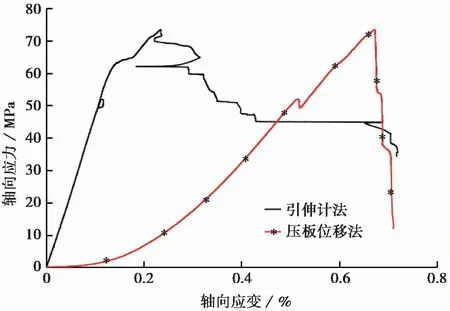
图5 花岗岩轴向引伸计和压板位移应力-应变曲线的比较

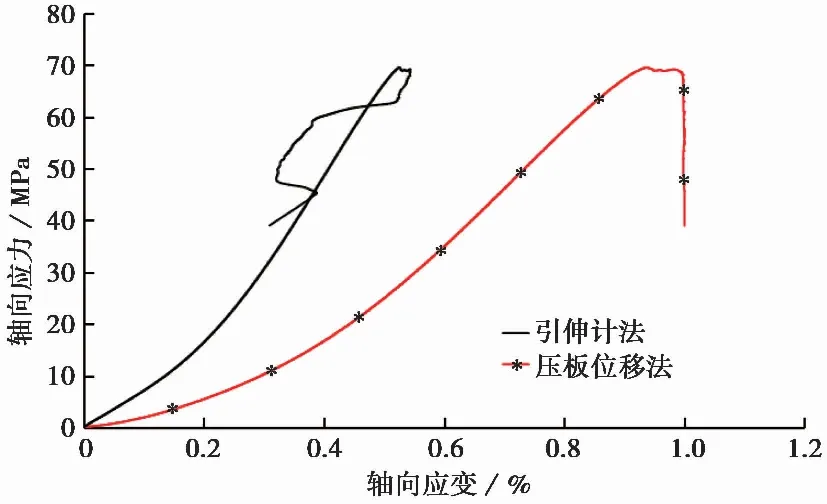
图6 玄武岩轴向引伸计和压板位移应力-应变曲线的比较

运用MTS试验机进行单轴压缩试验时，受试验设备等因素影响，试验结果往往有所偏差。其中一个主要影响因素来自加压过程中，岩样上下两个端面在受压后会与压头产生摩擦力，导致试样端部的应力分布复杂且不均匀，特别是端部的剪应力会阻止试样在端部的径向变形，造成岩样的侧面在不同高度下径向变形不同(薛俊华等，2008；麦戈等，2013；侯宏涛等，2015)。因此，端部效应对压缩试验的变形结果影响巨大。当采用引伸计进行测量时，引伸计标距测量的范围(50imm)在岩样中部，能够有效避免岩样两侧的端部效应，得到的变形结果更加客观准确。此外，引伸计直接接触试样，可以测量试样同一高度两组不同位置的轴向变形，得到的试样变形数据更为精准。由此可得，峰值强度前试样轴向应变应采用引伸计的测量结果。

图7显示了页岩在30iMPa围压下3种测量方法(引伸计、LVDT、压板位移)得到的应力-应变曲线。在三轴试验中，LVDT和压板位移所测得的轴向应变变化轨迹基本相同，LVDT测量得到轴向应变与压板位移测量得到的轴向应变相比略小一些，两种测量方法得到的轴向应变都远大于引伸计测量所得的轴向应变。这些发现与Munoz et al.(2016)在研究砂岩轴向应变得到的结果一致。

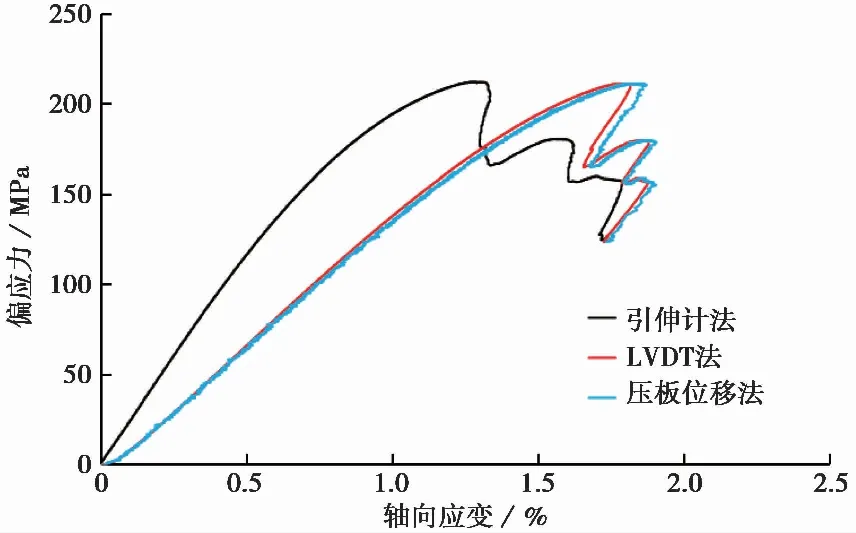
图7 页岩三轴压缩试验的全应力-应变曲线的对比

由上述分析可知，在峰值强度前，与LVDT、压板位移测量的变形结果相比，引伸计测量结果更为科学合理。

2.2 应力-应变曲线峰值后数据分析

在图4大理岩单轴压缩试验的应力-应变曲线中，当轴向压力达到峰值强度后，由引伸计测量得到的轴向应变时而增大时而减小，显然这样的曲线不符合轴向位移控制方式的预期变化(采用轴向位移控制时，轴向应变应当表现出持续增大的变化趋势)。

为了分析峰值强度后轴向应变(引伸计测量结果)不规则变化的原因，本节分别分析引伸计测量的两组轴向位移的变化趋势，如图8。由图8可知，根据引伸计B得到的应力-应变曲线，在曲线的峰后阶段也出现了轴向应变减小的现象，随着应力下降轴向应变从正值变为负值；而由引伸计A测得的数据，曲线上没有发生类似现象，尽管轴向应变在峰后阶段出现了不规则变化，大体上轴向应变随加载的进行而继续增大。由此可见，引伸计法得到的两组变形数据在峰后阶段并不相同，两组数据的趋势恰好相反，这也导致了图4引伸计在峰后阶段轴向应变出现不规则变化。

图8 轴向引伸计A、B的应力-应变曲线的比较

结合图9进一步分析引伸计获得的轴向变形减小的原因。岩样在达到峰值强度后，大理岩会发生宏观断裂，岩样被贯穿的裂隙面分为两个单独的岩块，此时引伸计测量的数据变为岩块的变形，而并非试样整体的轴向变形。对于岩块而言，轴向应力的跌落意味着卸载，峰值后的轴向应力要小于峰值强度，因而岩块的变形量会减小，即引伸计测得的数据呈现减小的变化趋势。由此可见，峰值强度后引伸计测得的轴向变形不能代表试样真实的变形量。

图9 岩样破坏及LVDT安装示意图

为了得到应力-应变曲线在峰值应力后准确的轴向应变值，建议在试验机固定压头上安装LVDT位移传感器进行测量，如图9所示。LVDT测量的数据为试样整体的变形值，并不包含压头或垫块的变形量。同时，LVDT传感器有着良好的环境适应性，可以在高油压、高温条件下稳定工作(刘晓宇，2015)，满足三轴压缩试验的要求。通过LVDT传感器测量得到的峰值应力后轴向应变的数值更符合整个岩样在破坏后真实的变形情况。

如果试验设备无法满足安装LVDT传感器，则可以采用压板位移测量得到的变形数据表示峰后阶段的轴向应变。理论上来说，压板位移包含了压头以及垫块本身的压缩变形、及两者之间接触缝隙的位移量，然而峰值强度后，在轴向应力发生显著跌落时，压头以及垫块在轴向压力的作用下变形量已经非常微小，两者之间的缝隙已被压实，可以忽略不计。由图7中曲线在峰值应力后的图像可以看出，压板位移的轴向应变同LVDT测量得到的轴向应变十分接近，压板位移在峰后阶段获取的数据也可表明岩样的真实轴向位移。

基于上述研究，引伸计测量的变形数据在应力-应变曲线的峰后阶段不可取。为了得到曲线在峰值应力后良好的轴向应变值，建议在试验机安装LVDT传感器，通过LVDT传感器测量得到的峰值强度后的变形数据可以清楚表明试样的轴向变形量。当条件不允许安装LVDT传感器，可以采用压板位移测量的变形数据来代替。

2.3 强度及变形参数分析

岩石的起裂强度(σci)、损伤强度(σcd)两个材料参数对岩石内部裂缝扩展机制和强度破坏机制分析具有重要的意义(周辉等，2014)。弹性模量E和泊松比ν是表征岩石变形特性的重要指标。

由2.1节中的分析可知，峰值强度前应采用引伸计测量的变形数据计算轴向应变，若采用LVDT、压板位移两种方法计算得到的数据则存在一定偏差。通过计算3种测量方法下损伤强度(σcd)、起裂强度(σci)、弹性模量E和泊松比ν，分析LVDT、压板位移与引伸计测量数据之间的误差，如表1所示。

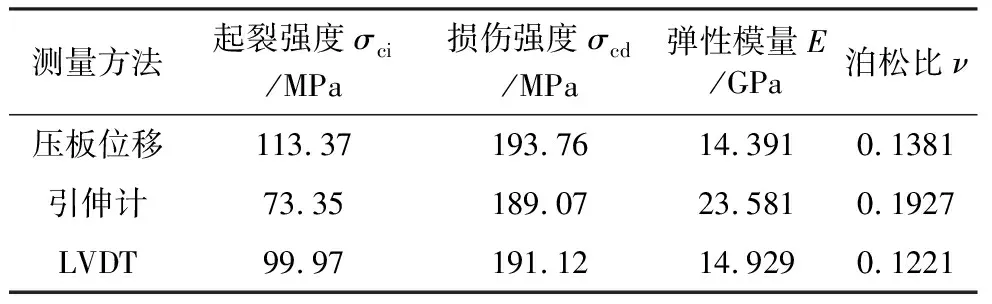
表1 页岩三轴压缩试验3种测量方法下的强度及变形参数统计表

其中，起裂强度σci通过式(1)～式(3)计算裂纹体积应变εvc来确定(张晓平等，2011)：

(1)

εv=ΔV/V≈εaxial+2εlateral

(2)

εvc=εv-εve

(3)

式中：ΔV，Velastic分别表示为岩样体积和岩样弹性体积；ε、εlateral、εve和εv分别为轴向应变、径向应变、弹性体积应变和总体积应变。起裂强度所对应的应力为裂隙体积应变将要开始增加时的轴向应力。损伤强度σcd对应的应力为体积应变曲线拐点时的轴向应力(周辉等，2014)。弹性模量和泊松比采用应力-应变曲线线弹性阶段的数据计算(胡广等，2016)。

根据表1可以看出，3种方法对应的损伤强度非常接近，这表明通过LVDT、压板位移两种测量方法定位体积应变的拐点误差不大。相反，对于起裂强度测量的数值则相差甚远，其中，压板位移测得的起裂强度值要比引伸计测得的起裂强度值大40iMPa，LVDT测得的起裂强度值要比引伸计测得的起裂强度值大20iMPa。这说明通过LVDT或压板位移计算裂纹体积应变得到的起裂强度很难保证其精确度。

由压板位移和LVDT计算得到的弹性模量十分相近，但相比引伸计计算得出的弹性模量要小40%，两者测量的结果都存在较大误差。引伸计测量岩样中部变形，这一部分的变形比较均匀，计算得到的弹性模量更加客观准确。这一结果同样适用于泊松比，由压板位移或LVDT算出的泊松比和引伸计计算得出的泊松比相差30%左右，计算结果存在一定偏差。

由此可见，对比起裂强度、损伤强度、弹性模量和泊松比的数据结果，压板位移和LVDT计算得到的数据存在一定的误差，建议使用引伸计测得的强度和变形参数。

3 讨论

采用轴向位移加载控制方式下引伸计测量得出的应力-应变曲线形状与Ⅱ类曲线的形状相似，通常会被误认为这种曲线属于Ⅱ类曲线(如图4应力-应变曲线所示)。经过分析，由于引伸计测得的曲线在峰后阶段出现了轴向应变减小的现象(如图8引伸计B所示)，峰值强度后的数据不能反映岩样的真实轴向变形。本文的三轴压缩试验采取的控制方式为径向变形加载控制，引伸计测得的曲线符合岩石的Ⅱ类曲线。对比两类控制方式得到曲线可以看出，采用轴向控制方式无法得到Ⅱ类曲线只能得到Ⅰ类曲线，Ⅱ类曲线只有采用径向变形控制方式获取。这与Wong et al.(2019)研究的结果相同，岩石Ⅱ类曲线的产生，不仅与岩体本身固有的性质，同时与岩样的加载控制方式有关。关于岩石Ⅱ类曲线产生的原因，除了加载控制方式的影响因素外，MTS试验机测试系统的刚度、试样的高径比、加载时的速率、包括岩石本身的性质都对应力-应变曲线的形态有着不可忽略的影响(戴罡，2015；Vogler et al.，2016；Wong et al.，2019)。