化学溶液作用下基于压实膨润土孔隙结构演化的土水特征模型研究*
2022-05-11卢普怀滕继东叶为民
贺 勇 卢普怀 滕继东 叶为民
(①中南大学,有色金属成矿预测与地质环境监测教育部重点实验室,长沙 410083,中国)(②同济大学,岩土及地下工程教育部重点实验室,上海 200092,中国)(③中南大学,土木工程学院,长沙 410075,中国)
0 引 言
据中国核能行业协会发布的《中国核能发展报告(2020)》,我国2019年核能发电量为3481.31亿千瓦时,同比增加18.09%,各类电源发电量中,核电占比上升至4.88%(王毅韧,2016)。与此同时,我国高水平放射性核废物(高放废物;HLW:high level radioactive waste)的产生速率随之快速增长(叶为民等,2017,2018,2020;刘樟荣等,2020a)。为实现HLW的安全处置,我国选择了建设高放废物深地质处置库(DGR:deep geological repository)的方案,并在设计中将具有低渗透性、高膨胀性、强吸附性、热稳定性、耐辐射性以及经济性的压实膨润土作为DGR中首选的缓冲/回填材料(刘樟荣等,2020a,2020b;Ye et al.,2018,2020)。然而,在DGR内部上万年的化学溶液入渗和干湿循环过程中(He et al.,2015;Al-Badran et al.,2017;He et al.,2019a,2019b,2020),压实膨润土长期处于非饱和状态,其双孔结构(大孔和小孔,或集聚体间孔隙和集聚体内孔隙)受化学因素影响而发生变化,严重影响其工程屏障性能。
土水特征曲线(SWRC:soil water retention curve)是研究非饱和土中水分流动和溶质运移的基础,其反映了土体含水量(饱和度)与吸力之间的关系,被广泛应用于评价非饱和土渗透系数、抗剪强度、体积变形等工程性质(Ye et al.,2009;Wang et al.,2019)。在初始干密度、土体结构、温度、应力历史和孔隙水化学等因素的影响下,非饱和土的SWRC具有不同形态(单峰、双峰或多峰)和变化规律(Alonso et al.,2005;李同录等,2019;Qiao et al.,2019;潘登丽等,2020;周翠英等,2020)。Lloret et al.(2007)通过试验和模型拟合的方式研究了侧限条件和干密度对压实膨润土SWRC的影响,结果表明,干密度主要影响试样中大孔的含量,因此在由小孔持水的高吸力阶段,不同干密度下的SWRC趋于重合。毛尚之(2002)研究了应力历史对膨胀土SWRC的影响,结果表明,吸力相同时,未固结土样的含水量大于固结土样,其内在因素也是孔隙结构的改变。Habasimbi et al.(2018)研究了围压对压实日本黏土SWRC的影响,表明随着围压增加,土样的宏观孔隙比减小,且其减小速率逐渐降低,SWRC的滞回现象越不明显。众多学者通过试验研究了化学溶液对压实膨润土SWRC的影响,表明盐溶液能抑制扩散双电层的形成,从而改变土体持水性能(Mokni et al.,2011;Musso,2013)。由此可见,土体宏观SWRC的差异性根本在于其微观结构的改变,从土的粒径组成和孔径分布的角度探究各因素对SWRC的影响有助于理解其本质机理。
在对SWRC的描述上,尽管建立了相关的拟合方程,但通过试验和曲线拟合的方式获取SWRC存在既耗时又不经济的问题,因此,一些学者尝试构建SWRC预测方程,从而使SWRC的测定转换为简单土性参数(如粒径分布、孔径分布等)的获取问题(Hu,2013;Ye et al.,2018)。考虑到从粒径分布预测SWRC的模型往往低估SWRC在非饱和段的含水量,一些学者对模型进行改进和验证,结果表明基于粒径分布预测SWRC最终仍取决于土体孔径分布的计算精度(Scheuermann et al.,2007;Chang et al.,2019)。压实膨润土中的孔隙水主要以毛细和吸附的方式分布在集聚体间孔隙和集聚体内孔隙中,有学者依据压汞试验结果建立的SWRC预测模型可反映某些土体SWRC的“双峰”特征(如图1所示),表明基于双孔理论推导SWRC能较好地反映试样中大孔水和小孔水的分布规律(Ghanabarian-Alavijeh et al.,2010;Niu et al.,2019)。
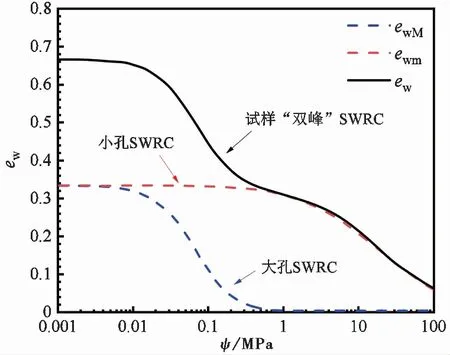
图1 考虑压实膨润土双孔结构的SWRC
此外,分形几何在非饱和土微观分析中的应用,为建立参数物理意义明确、实效性高的SWRC预测模型提供了新的理论基础。国外以Bird为代表,建立了基于土体“孔隙-固体分形”特性的SWRC预测模型(Bird et al.,2008);国内徐永福等(2002)较早研究了土体的分形特征,根据土体孔隙分布的分形特征,提出了SWRC预测模型的通用表达式。近年来,杨明辉等(2019)基于分形理论分析了SWRC的滞回现象,Tao et al.(2019),Huang et al.(2005)建立了土体SWRC分形预测模型,分析了干湿循环、吸力、压实功对分形维数的影响,表明分形维数随吸力和干密度的增加而增大。实际上,孔隙化学溶液也会造成压实膨润土孔隙结构的改变,造成分形维数的变化。然而,目前针对化学溶液影响下的SWRC研究较少,且缺少基于不同理论建立的SWRC预测模型在相同化学条件下的对比研究。
本文基于分形理论和双孔理论,建立了两种基于压实膨润土孔径分布的SWRC预测模型,利用He et al.(2016)测得的不同浓度NaCl溶液处理土样的压汞试验数据,预测了相应工况下的土水特征曲线,并与实测曲线进行对比,比较了两种模型的预测效果。最后,在上述过程的基础上,从微观角度分析了化学溶液对压实膨润土SWRC的影响机理。
1 模型建立
一般地,在建立化学溶液影响的压实黏土土水特征预测模型时,可采取两种方法:(1)直接建立含水量与基质吸力(孔径)、土性及溶液浓度的函数方程;(2)建立含水量与基质吸力(孔径)的函数方程,再用化学溶液处理土样的压汞试验数据对模型进行验证。前者建立的模型中参数较多,对土性参数的精度要求较高;而后者建立的模型中参数较少,只与孔隙结构相关,且众多学者通过试验发现,化学溶液对土样持水特性的影响主要是通过改变其孔隙结构实现的,故通过该方法建立的模型适用性较强。本文采用方法(2)建立模型,同时考虑到基于分形理论推导的SWRC模型相较于一般的经验模型更容易确定模型参数的物理意义(杨明辉等,2019);而基于双孔理论推导的SWRC预测模型更能反映压实膨润土的实际孔隙结构(Hu et al.,2019)。因此,本文基于上述两种理论建立SWRC预测模型。
1.1 基于孔径分布和分形理论的SWRC预测模型
土体是一种具有多层统计自相似的分形体,Huang et al.(2005)指出,土中固体颗粒相和孔隙相的分形特征主要表现为:(1)粒度分形,包括孔径分形及粒径分形;(2)表面分形;(3)质量分形,包括固体质量分形和孔隙质量分形;(4)孔隙-固体分形。基于“孔隙-固体分形”性质建立的SWRC模型具有一般性,能作为建立新模型的基础。
假设土样的总孔隙率为ntotal,在压汞试验的土-汞-气系统中,大于di(m)的孔隙被汞填充,所占的孔隙率为n(>di)。依据分形理论(Bird et al.,2008),n(>di)和ntotal的表达式分别为:
n(>di)=β(1-(di/dmax)3-D)
(1)
ntotal=θs=β(1-(dmin/dmax)3-D)
(2)
式中:D为分形维数,即描述分形自相似性的几何参数,常用计盒法进行定义(王康,2009);θs为饱和体积含水量;β为模型参数,范围为[0,1];dmin和dmax分别为土中最小和最大孔隙直径(m)。
而在SWRC测定试验的土-水-气系统中,小于等于di的孔隙被水填充,则土样的体积含水量θw可表示为:
θw=ntotal-n(>di)
=ntotal-β(1-(di/dmax)3-D)
(3)
根据Young-Laplace方程,在SWRC测定试验中,水和空气的接触角α=0°,水的表面张力Ts=0.072 N·m-1。基质吸力ψi(Pa)与孔径di(m)满足关系:
(4)
则式(3)可以表示为:
θw=ntotal-β(1-(ψAEV/ψi)3-D)
(5)
式中:ψAEV为土样的进气值(Pa),与孔径dmax对应。
根据质量含水量ω与体积含水量θw的关系:
ω=(1+e)θw/Gs
(6)
将式(5)的θw替换为ω,得:
(7)
式中:e为孔隙比;Gs为土颗粒比重。
式(7)的适用条件为:dmin
(8)
1.2 基于孔径分布和双孔理论的SWRC预测模型
如图2所示,膨润土是一种主要由蒙脱石矿物组成的高膨胀性黏土,其微观结构层次由大到小依次包含:大颗粒、集聚体、层叠体、片晶层等。其中:集聚体是由多个层叠体和层叠体间孔隙构成的集合体。Delage et al.(1984)将压汞试验(MIP)与扫描电镜法(SEM)结合,在试验中观测到膨润土内存在集聚体内孔隙(小孔)和集聚体间孔隙(大孔),众多学者用其他类型压实黏土进行试验,观察到类似的双孔隙结构(Alonso et al.,2005;Mokni et al.,2011;Musso et al.,2013)。因此,通常采用双孔理论描述压实膨润土的孔隙结构。
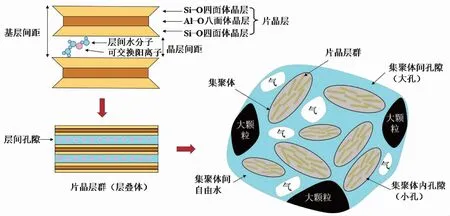
图2 膨润土微观结构示意图(修自Nasir et al.(2017))
压实膨润土的孔径分布可用概率函数的形式表示,孔径积分函数F(d)与孔径分布之间的关系为(Della et al.,2015):
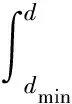
(9)
式中:f(x)dx代表单位体积土体中直径在[x,x+dx]范围内的孔隙所占的百分比;F(d)代表单位体积土体中直径小于d的孔隙所占的百分比。
压汞试验测定的孔径范围为[dmin,dmax],在此范围之外的孔隙对孔径积分函数F(d)的影响较小,故:
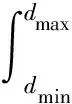
(10)
在土-水-气系统中,小于d的孔隙被水填充(Della et al.,2015),此时的相对饱和度Sr(d)为:
(11)
式中:θ(d)为当前体积含水量;θr为残余体积含水量;θs为饱和体积含水量。
ew(d)定义为被水填充的孔隙体积Vw所占的孔隙比:
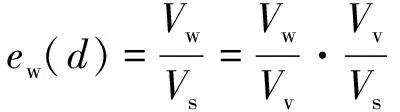
=Fe(d)
(12)
式中:Vs为土颗粒占据的体积;e为总孔隙比。
由van Genuchten模型(Van Genuchten,1980):
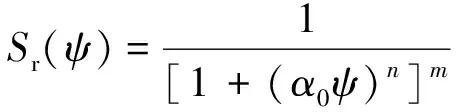
=Sr(d)
(13)
式中:α0、m、n为模型参数,m=1-1/n。
考虑双孔效应,在小于d的孔隙中,既有集聚体间孔隙,也有集聚体内孔隙,故可将小于d的孔隙所占的孔隙比表示为:
ew(d)=Fe(d)
=ewm(d)+ewM(d)
(14)
式中:ewm(d)和ewM(d)分别为直径小于d的孔隙中集聚体内孔隙和集聚体间孔隙的孔隙比;em和eM分别为整个土样中集聚体内孔隙和集聚体间孔隙的孔隙比;Srm(d)和SrM(d)分别为相应情况下的饱和度。
由van Genuchten模型(Van Genuchten,1980),得:
(15)
(16)
式中:α0 m、mm、nm、α0M、mM、nM为拟合参数,mm=1-1/nm,mM=1-1/nM。
再结合式(4)、式(13)和式(14),得:
=ew(ψ)
(17)
由于将土中孔隙划分为大孔和小孔,故孔隙比e与em和eM之间满足如下关系(Dieudonné et al.,2016):
e=em+eM
(18)
为便于与双孔模型进行对比,将ew(d)转化为质量含水量ω。则基于孔径分布与双孔理论的土水特征模型(简称为双孔模型,下同)可表示为:
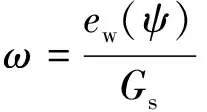
(19)
上式中的em可根据累计压汞曲线求得:
em=GsVzmρw
(20)
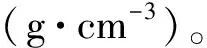
2 模型验证
2.1 试验工况及数据
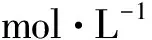
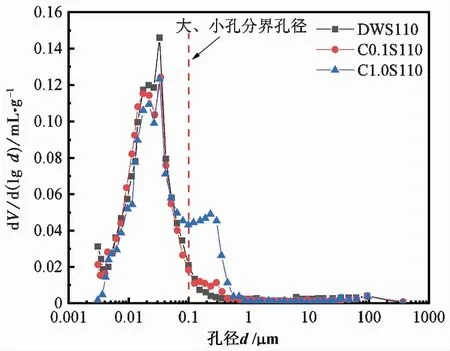
图3 压实GMZ膨润土(ρd=1.7 Mg·m-3)的孔径密度曲线(He et al.,2016)
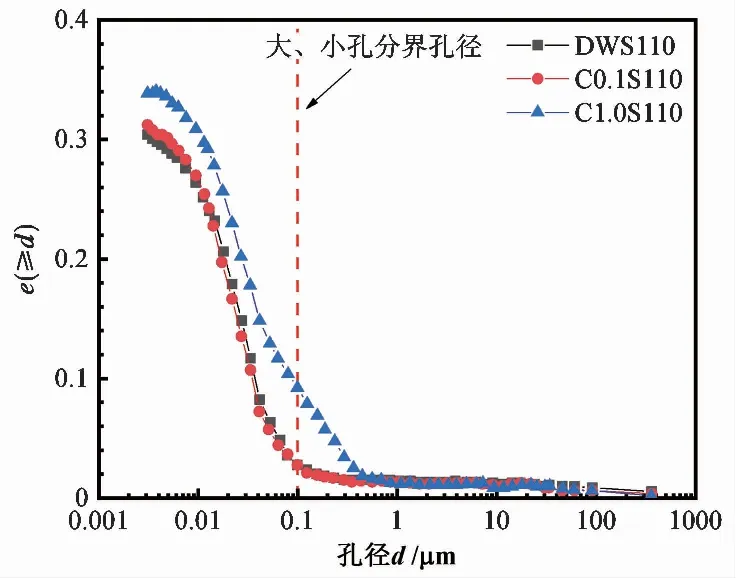
图4 压实GMZ膨润土(ρd=1.7 Mg·m-3)的累计压汞曲线(He et al.,2016)
2.2 模型假设及计算
对于压汞试验获得的孔径分布曲线,需经过适当处理后,才能得到相应的基质吸力与含水量数据,本文在模型计算中采用如下假设:
(1)计算中忽略压汞试验误差,认为汞开始侵入的孔径即为dmax。
(2)采用孔径密度曲线(PSD)最低谷对应的孔径作为大、小孔分界孔径,即孔径小于0.1 μm的孔隙为小孔,大于0.1 μm的为大孔(Romero et al.,2011;He et al.,2016)。
(3)由于本试验中用于压汞试验的试样与用于测定SWRC的试样同时经历了一次干湿循环,并最终处于稳定状态,故假设由于两种试验中试样体积不同造成的基质吸力的差异已不明显,采用式(4)计算基质吸力。
本试验的累计压汞曲线是以e(≥d)(孔径大于d的孔隙所占的孔隙比)为纵坐标,通过下式将其转化为质量含水量:
(21)
式中:e为控制吸力为110 MPa时试样的孔隙比。
由于总吸力为基质吸力(ψi)与渗透吸力(π)之和,因此可采用总吸力减去渗透吸力的方式获取模型中的基质吸力,其中:渗透吸力采用如下经验公式计算:
π=iRTC
(22)

2.3 模型预测及验证
根据He et al.(2016)的数据和2.2节中的假设,求得对应的含水量和基质吸力数据,再用所建立的分形模型和双孔模型分别进行拟合,得到的预测结果如图5和表1,表2所示:
图5 基于He et al.(2016)孔径分布数据预测的压实GMZ01膨润土SWRC
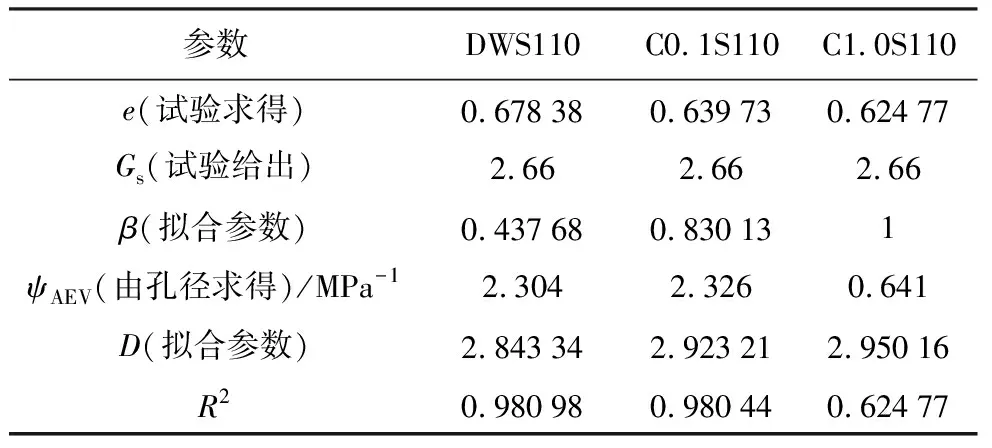
表1 分形模型参数
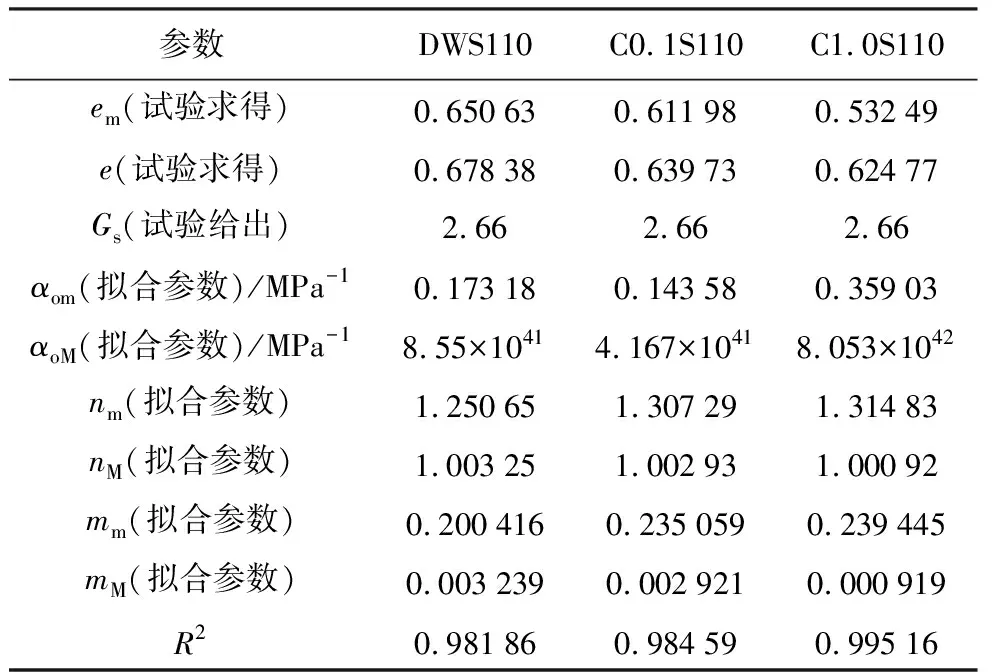
表2 双孔模型参数
He et al.(2016)通过试验直接测定了用饱和度与总吸力表示的侧限条件下压实GMZ膨润土的SWRC,本文将其转化为用质量含水量与基质吸力表示的SWRC,实测和预测的SWRC如图6所示。

图6 预测的SWRC与实测SWRC比较
图5表明,基于He et al.(2016)测定的压实GMZ01膨润土孔径分布数据预测的SWRC为“单峰”曲线,可从微观结构的角度分析产生该现象的原因:由于He et al.(2016)在对试样进行压汞试验前试样已经经历过一次干湿循环,集聚体间孔隙减小,集聚体内孔隙增大,试样的孔隙趋于均一化,压实膨润土的双孔结构逐渐消失,导致土水特征曲线表现为“单峰”曲线。在此情况下,分形模型和双孔模型的预测结果差别较小。
如图6所示,当吸力大于1.0 MPa时,预测SWRC曲线与实测曲线趋于重合,而当吸力小于1.0 MPa时,实测SWRC高于预测SWRC,说明在低饱和度范围内,单独通过孔径分布预测的膨润土持水性偏低,分析其原因主要与压汞试样的孔隙结构有关:由图3可知,本试验中的DWS110试样和C0.1S110试样的孔径密度曲线只有一个峰值,且其落于小孔范围内,可认为此时试样的持水作用主要由小孔主导;C1.0S110试样的孔径密度曲线虽然有两个峰值,但是大孔峰值对应的孔径已十分接近分界孔径,并低于小孔峰值,也可认为孔隙水大部分分布于小孔中。因此在饱和度较高的范围内,随吸力增大,小孔并不发生失水,只有当吸力增大到一定程度时,小孔才发生失水,曲线开始下降。而用于实测SWRC的压实膨润土试样在最初的饱和阶段是具有较明显的双孔结构的,在低吸力范围内,大孔和小孔同时持水,故试样的含水量高于仅通过小孔持水的压汞试样;而在高吸力范围内,大孔已完全去饱和,小孔开始失水,此时实测SWRC与预测SWRC趋于重合。
由表1可知,在本文所选试验的浓度范围内,压实GMZ膨润土的分形维数在2~3之间,符合细粒土的分形维数特征(王康,2009),随着溶液浓度的增加,在水化过程中,孔隙变得均匀,分形维数增大;由表2可知,随浓度的增大,α0 m和α0 m均先减小后增大,两者分别与小孔和大孔进气值的倒数有关,说明盐溶液作用下,试样的大小孔均先减小再增大,然而,由于试验的浓度组数较少,无法准确反映化学溶液对SWRC预测模型的影响规律。
综上所述,化学溶液对压实膨润土SWRC的影响主要是通过改变土样孔径分布实现的,因此本文基于孔径分布建立了两种模型,并用化学溶液处理后压实膨润土的孔径分布数据进行了验证。结果表明:两种模型均能满足预测化学溶液影响下压实膨润土SWRC的基本要求。为提高模型的准确性和灵敏度,在模型中引入溶液浓度参数将是今后的研究重点。
3 结 论
(1)依据分形理论和双孔理论分别建立了压实膨润土SWRC预测模型,利用He et al.(2016)的试验数据进行SWRC的预测和验证,结果表明两种模型预测效果均较好且相近。然而,由于压汞试验前的干湿循环使试样内部孔隙均一化,双孔模型的预测曲线只有一个峰值。
(2)预测SWRC在吸力低于1.0 MPa范围内的含水量低于实测值,在吸力高于1.0 MPa范围内与实测SWRC趋于重合。其主要原因为压汞前的干湿循环使试样孔隙分布在小孔范围内,作为预测数据来源的压汞试样只有小孔持水,而实测试样在低吸力范围内由两种孔隙持水,在高吸力范围内由于大孔去饱和,转为小孔持水。
(3)与蒸馏水处理后相比,盐溶液导致压实膨润土集聚体间孔隙减小,在相同基质吸力下试样的含水量降低;但在高浓度盐溶液处理后,由于孔隙流体通道增加和压实膨润土内部产生微裂隙,试样在高吸力范围内的持水能力略有增大。
(4)基于压实膨润土孔隙结构演化的土水特征模型能较好地反映化学溶液对压实膨润土持水性的影响规律,但在局部吸力段,预测模型对高浓度溶液引起的孔隙结构变化灵敏度不足,在今后对模型改进的研究中,需考虑对所建模型引入溶液浓度参数。
