基于动态Verhulst模型对高层建筑沉降预测的应用研究

滕 雷，魏长寿，王俊杰，王仁锋

(1.山东科技大学测绘与空间信息学院，山东青岛 266590;2.内蒙古科技大学矿业与煤炭学院，内蒙古包头 014010;3.庆云县第二中学，山东德州 253700)

1 引 言

随着经济社会快速发展，城市现代化进程加快，高层建筑如雨后春笋般出现，其安全问题也倍受人们关注。对高层建筑进行沉降预测，可判断其沉降趋势，对防灾减灾有着重要的研究价值[1]。当前，灰色理论被广泛应用于沉降预测领域[2-4]。刘丹丹[5]提出应用GM(1，1)模型对高层建筑进行沉降预测；张明远[6]等应用改进后的GM(1，1)模型进行沉降预测，虽然证明了GM(1，1)模型适用于高层建筑的沉降预测，但是GM(1，1)模型预测呈指数形式，后期预测效果不理想。张庆伟[3]分别应用Verhulst模型和GM(1，1)模型对高层建筑进行沉降预测，验证了前者精度更高、适用性更强。Verhulst模型是德国生物学家Verhulst提出的一种特殊灰色模型，主要用来描述具有饱和状态的过程[7]。土力学理论证明，高层建筑的沉降与时间关系具有饱和状态“S”形曲线[8]。鉴于此，本文基于Verhulst模型对高层建筑进行沉降预测，并对其进行动态改进。以青岛某大厦沉降数据为研究对象，分别采用GM(1，1)模型、Verhulst模型和动态Verhulst模型对沉降数据进行拟合和预测。

2 模型的建立

2.1 数据预处理

等时距数据序列是Verhulst模型建模的基础要求，但由于监测方案的制定或其他因素的影响，观测的沉降数据往往很难满足该要求。本文利用牛顿分段线性插值法进行数据预处理，实现非等时距数据等时距化[9]。设实测数据序列为：X(t)=[x(t1)，x(t2)，…，x(tn)] 。

1)计算平均时间间隔Δt：

(1)

2)等时距变化量的计算：

(2)

(3)

2.2 Verhulst模型建立

对经数据预处理获得的数据X(0)做一次累加得X(1)，定义a、b为模型待定参数，B、Y为模型参数矩阵。则Verhulst模型方程为[3]：

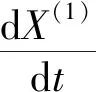
(4)

其唯一解为：

(5)

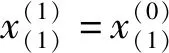
[a，b]T=(BTB)(-1)BTY

(6)

2.3 动态Verhulst模型建立

2.4 精度检验

本文采用后验差法[2]和外符合精度[11]分别对模型精度和预测精度进行评定。后验差法评定标准如表1所示。

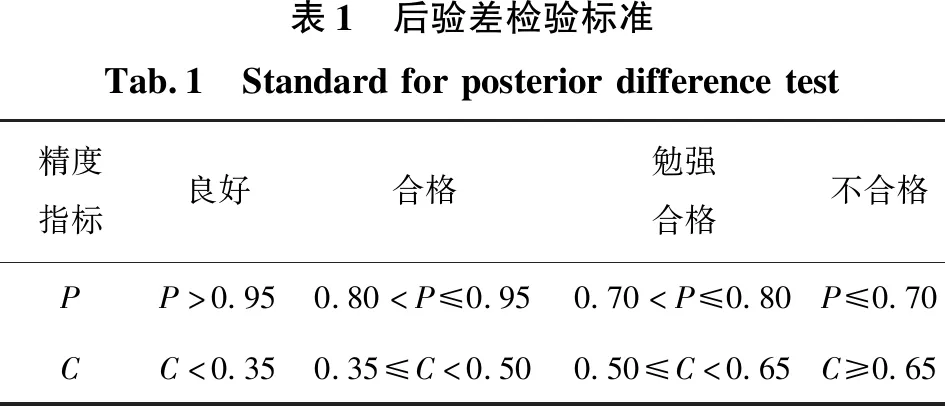
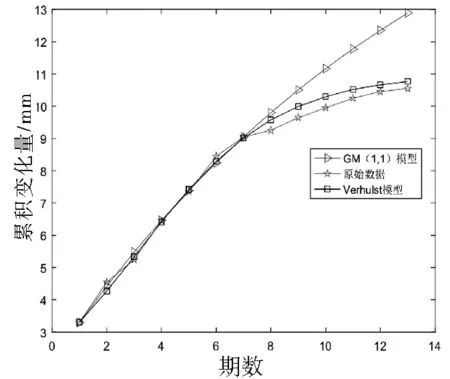
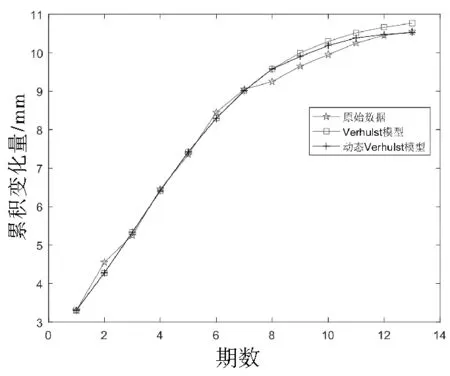
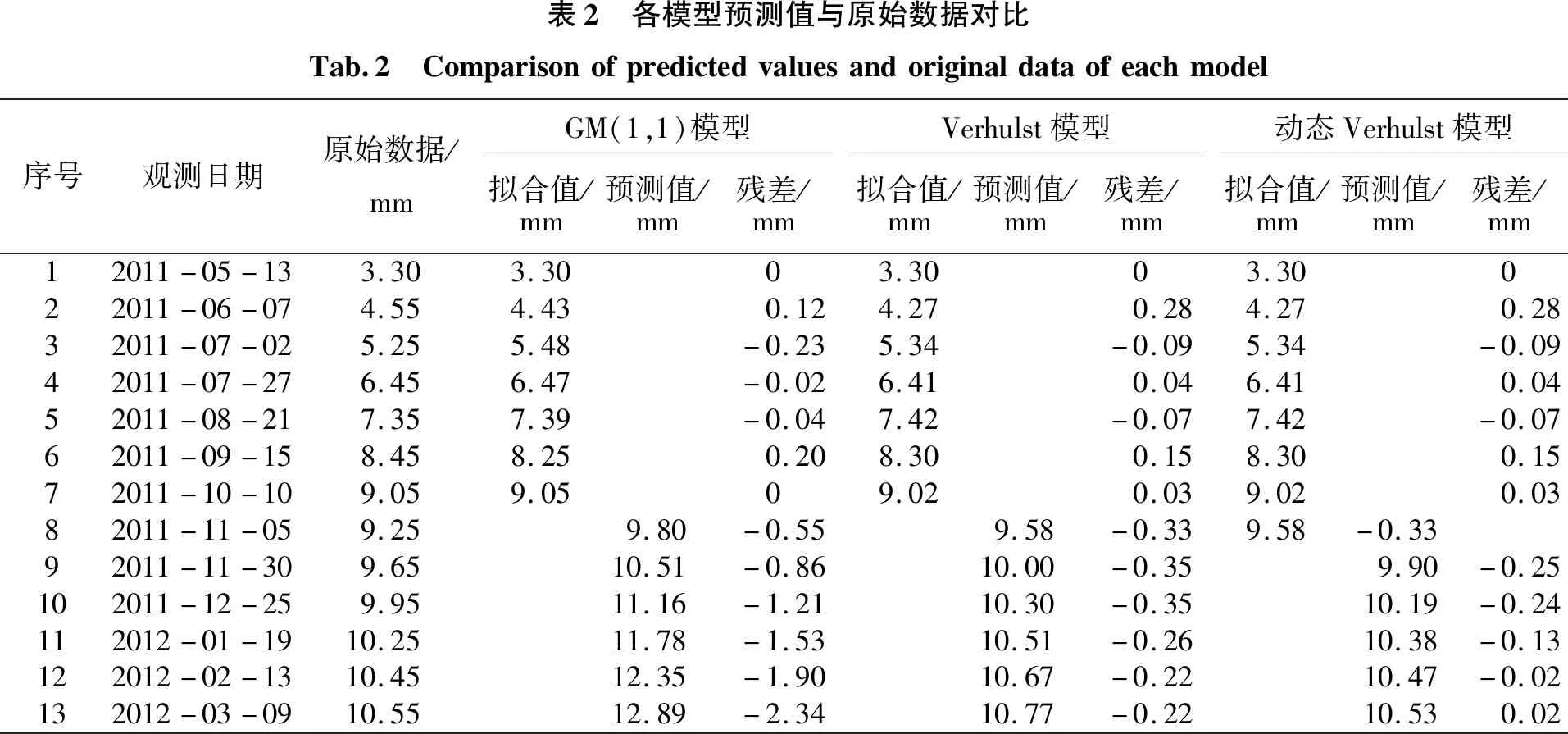
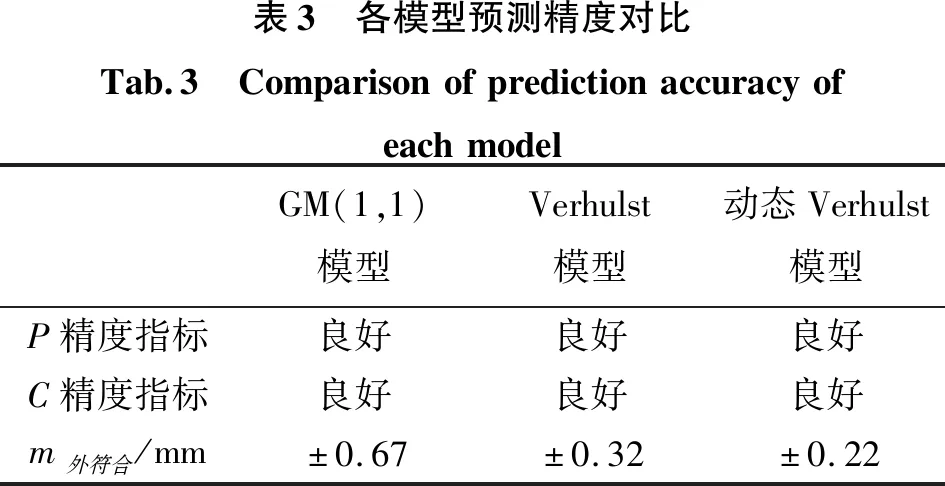
表1 后验差检验标准Tab.1 Standardforposteriordifferencetest精度指标良好合格勉强合格不合格PP>0.950.80

外符合精度计算公式为：

(7)

3 算例

3.1 工程概况

青岛某大厦位于经济技术开发区，工程勘察面积约28 365 m2，拟建1栋19层高层楼房，建筑高度66 m，直接坐落在天然地基上，基础为筏板基础，主体为框剪结构。为保障工程安全，在施工初期布设了12个沉降观测点，点号为H1～H2。监测方案要求每施工一层观测一次。

3.2 Verhulst模型预测

由于监测方案要求每施工一层检测一次，获得的沉降数据为非等时距的数据序列，应用Verhulst模型预测沉降，需利用牛顿插值法进行数据预处理。现以沉降观测点H11为例，经数据预处理后得到等时距的原始数据如表2所示。基于前七组数据建立Verhulst模型，对后六组数据进行沉降预测。由式(5)、(6)可得：

[a，b]T=(BTB)-1BTY=[0.394 1 0.035 9]

(8)

(9)

由此可得Verhulst模型的预测结果，如表2、表3及图1所示。表中Verhulst模型的P、C精度指标均达到良好，最大残差值为-0.35 mm，GM(1,1)模型的最大残差值为-2.34 mm；从图1中可以明显看出，GM(1,1)模型的曲线呈指数型增长，而Verhulst模型的曲线相对平行于原始数据曲线，变化趋势较一致。

图1 Verhulst模型预测Fig.1 Prediction diagram of Verhulst model

3.3 动态Verhulst模型预测

[a，b]T=(BTB)-1BTY=[0.345 7 0.030 2]

(10)

(11)

图2 动态Verhulst模型预测Fig.2 Prediction diagram of dynamic Verhulst model

表中动态Verhulst模型的残差值越来越小，且每期均小于Verhulst模型，由外符合精度值可知，动态Verhulst模型的预测精度较Verhulst模型提高30%；由图2可以看出，动态Verhulst模型的曲线在原始数据曲线和Verhulst模型曲线之间，且随时间变化越来越接近于原始数据。

表2 各模型预测值与原始数据对比Tab.2 Comparisonofpredictedvaluesandoriginaldataofeachmodel序号观测日期原始数据/mmGM(1,1)模型拟合值/mm预测值/mm残差/mmVerhulst模型拟合值/mm预测值/mm残差/mm动态Verhulst模型拟合值/mm预测值/mm残差/mm12011-05-133.303.3003.3003.30022011-06-074.554.430.124.270.284.270.2832011-07-025.255.48-0.235.34-0.095.34-0.0942011-07-276.456.47-0.026.410.046.410.0452011-08-217.357.39-0.047.42-0.077.42-0.0762011-09-158.458.250.208.300.158.300.1572011-10-109.059.0509.020.039.020.0382011-11-059.259.80-0.559.58-0.339.58-0.3392011-11-309.6510.51-0.8610.00-0.359.90-0.25102011-12-259.9511.16-1.2110.30-0.3510.19-0.24112012-01-1910.2511.78-1.5310.51-0.2610.38-0.13122012-02-1310.4512.35-1.9010.67-0.2210.47-0.02132012-03-0910.5512.89-2.3410.77-0.2210.530.02

表3 各模型预测精度对比Tab.3 ComparisonofpredictionaccuracyofeachmodelGM(1,1)模型Verhulst模型动态Verhulst模型P精度指标良好良好良好C精度指标良好良好良好m外符合/mm±0.67±0.32±0.22

4 结束语

鉴于高层建筑沉降规律和Verhulst模型曲线特征均呈“S”型曲线变化，本文提出了建立Verhulst模型应用于高层建筑的沉降预测，并采用“去旧加新”的思想对模型进行动态改进，通过实时更新数据建立动态模型来提高预测精度。采用数据预处理实现原始数据等时距化，解决了建模条件苛刻的问题，使模型在实际工程中得以广泛应用。结合实际工程案例研究表明，动态Verhulst模型可以很好地拟合高层建筑沉降的全过程，准确地预测沉降最终值，较GM(1,1)和Verhulst模型预测精度提高30%。因此，基于动态Verhulst模型对高层建筑进行沉降预测是可行的，预测结果精度较高，可靠性较强。

动态Verhulst模型弥补了传统Verhulst模型不能实时反映系统状态变化的不足，但动态建模中引入的“新”数据具有一定灰度，当需要进行长期预测时，灰度区间会累积增大，影响预测的效果。因此需要根据工程的进展，充分引入新的实测数据建立动态Verhulst模型，通过提高建模数据的准确度，提高预测精度。