基于灰色—小波神经网络模型的建筑物变形预测

王 坤

(中交第三航务工程局有限公司宁波分公司，浙江宁波 315200)

1 引 言

近年来，随着社会经济发展与城市建设不断推进，各种高层、超高层建筑物也不断涌现出来。在建造和长期的使用过程中，这些高层建筑物由于受到施工荷载、人为因素、地壳运动、冰雹降雨等恶劣天气因素影响，建筑物结构会发生细微的变形。随着时间的积累，这些变形可能会对人民群众的生命财产安全造成严重的威胁。在此情况下，实时、高精度的建筑物变形监测对于建筑物安全事故的有效避免显得十分重要[1]。作为3S核心技术之一，GNSS技术以自动化程度高、成本低等优势，近年来被广泛应用于建筑物变形监测中，并且可以对建筑物进行全天候、全天时的变形监测[2]。

建筑物变形监测为获取准确、可靠的包含变形信息的原始数据打下了基础，但考虑如何通过这些采集到的数据获取建筑物的变形趋势，表现变形监测的意义与作用也非常重要。目前，建筑物变形监测数据的处理方法较多，如人工神经网络模型、卡尔曼滤波模型、回归模型等[3]。但是单一算法构成的预测模型稳定性与精度不高，因此又有学者提出将多种预测模型进行组合得到组合预测模型，试验表明，组合模型预测处理得到的结果比单一的预测模型更好。文献[4]将神经网络模型与灰色模型进行结合，取得的预测效果较好。国内相关学者根据变形监测的时间序列变化特征，结合神经网络预测模型，并经过案例分析证明了各自模型的预测精确度。然而这些研究对于有变形时间序列的随机波动性分析较为不足，当数据数目较小、短时间数据波动性较大时，其预测结果易陷入局部最小，从而导致预测结果误差偏大。

因此，本文提出将灰色系统理论与小波神经网络理论相结合，构建组合模型，在对建筑物变化特性分析的基础上，应用灰色预测模型对建筑物变形时间序列优先预测，降低其随机波动性。随后应用分步式小波神经网络预测模型进行预测，通过高层建筑物变形监测数据对组合模型的稳定性与有效性进行检验，分析预测结果的精度和准确度。

2 灰色系统理论

灰色系统理论是对原始数据变化随机性的一种弱化，包括系统预测法、拓扑预测法、数列预测法等[5]。针对建筑物变形监测的特点，本文选取数列预测法进行变形预测，并且考虑到GM(1，1)模型在变形监测数据处理中的优势，选择GM(1，1)模型进行建筑物变形预测。

1)假设有一原始观测数据：X(0)={x(0)(1)，x(0)(2)，...，x(0)(n)}，x(0)(n)表示第n期观测值。

2)通过对原始观测数据进行累加，得到新的数列：X(1)={x(1)(1)，x(1)(2)，...，x(1)(n)}。

3)紧邻均值生成序列：z(1)(k)=1/2[x(1)(k)+x(1)(k-1)]，k=2，3，...，n，得到新数列：z(1)={z(1)(2)，z(1)(3)，...，z(1)(n)}。

4)通过对新序列构建白化方程，得到：

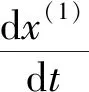
(1)

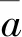
(2)

求解白化方程，得到：

(3)

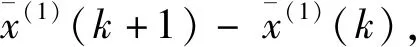
3 小波神经网络概述

作为一种对大脑处理信息方式的模拟，人工神经网络通过学习训练，在背景信息较弱的情况下，通过描述输入数据与输出数据之间的关系，可以表现强大的能力。当变形因素错综复杂，导致变形监测数据的诊断或预报不能通过准确的力学或者数学进行表示时，利用神经网络模型进行预测，就可表现其强大的优势。

3.1 小波神经网络模型结构

在BP神经网络模型的基础上，引入小波理论，通过小波理论中的尺度因子与平移因子，同时利用小波函数代替神经网络模型中隐含层的激励函数，提高神经网络模型的拟合能力和收敛能力，从而构成一种新的小波神经网络模型结构。

小波神经网络模型主要由3部分构成：一是输入层，二是隐含层，三是输出层，通过激励函数传递各节点之间的信息。与BP神经网络模型不同的是，小波神经网络模型利用小波函数代替激励函数，信号向前传播，与误差反向传播同时进行。本文使用的Morlet小波函数可表示为[7]：

(4)

式中：α为尺度因子，β为平移因子，f(x)为加权和。小波神经网络模型输出层可表示为：

(5)

式中：m表示输出层节点数，h(i)表示第i个隐含层的节点输出，wik表示隐含层到输出层的权值。为了使小波神经网络预测模型的输出值向期望的输出值不断逼近，利用梯度修正法对神经网络的权值和小波基函数参数进行不断修正。下列步骤为小波神经网络算法训练流程：

1)网络初始化。随机初始化网络连接权重wik、wjk以及伸缩因子ak、平移因子bk，同时对学习效率进行设置。

2)样本分类处理。样本分为两个部分，分别为训练样本和测试样本，对训练样本进行归一化处理后输入网络，并对网络预测的精度进行测试。

3)网络训练。将训练值输入网络模型中，计算期望输出值与预测输出值和输出值之间的误差。误差符合要求后，将预测值与权值输出。

4)权值修正。经过步骤3)后计算误差，如果误差不符合要求，则需对小波函数参数与网络权值进行修正，使预测值向期望输出值不断逼近。重复修正过程，直至误差符合要求为止。

5)完成训练获取预测值后，对预测值进行反归一化处理，得到最终预测值。

3.2 小波神经网络模型类型

根据形式，小波神经网络可分为两大类：一是辅助式小波神经网络模型，神经网络与小波分析分离。此时二者的关系是紧密联系且相互独立的，使用小波分析预处理数据，发挥小波分析的去噪功能。将去噪后的数据作为输入值输入神经网络中，小波分析的作用就是为模型去除噪声；二是嵌入式神经网络模型，此时小波分析与神经网络紧密联系在一起。使用小波函数替换激励函数，同样使用小波函数的平移因子与伸缩因子代替隐含层阈值及输入层到隐含层的权值。

4 实例分析

4.1 数据介绍

造成建筑物变形的因素有地壳运动、人为使用因素、气候因素等，故建筑物的变形通常是非线性、非稳定性的随机变形，并且具有不确定性和微弱性的特点。文献[8]在对变形监测数据分析的基础上对建筑物的变形进行分类，分为复杂变化型、匀速-增速型和减速-匀速型。其中复杂变化型会产生随机的位移突变，对此变形进行预测取得的效果较差；匀速-增速型和减速-匀速型变形较为平稳，伴随着一定的规律，对此类变形预测得到的结果精度较高。为了更好地验证本文提出预测模型的有效性，选择复杂变化型建筑物作为形变数据进行试验。图1所示为中交第三航务工程局有限公司承建的银川文化园项目融媒大厦(94.7 m高)顶变形监测点T1连续30期位移变形曲线，可以看出建筑变形曲线为复杂变化型，由于尚未结束施工，因此建筑的变形具有复杂性和不稳定性。

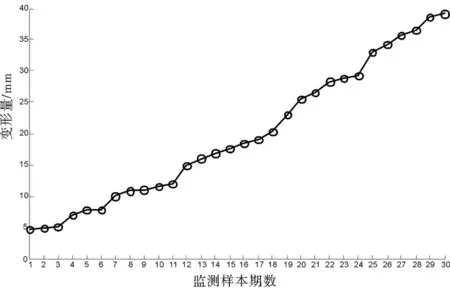
图1 融媒大厦30期形变数据曲线Fig.1 Deformation data curve of 30 phases

4.2 灰色—小波神经网络模型结构

小波分析可以对非线性函数进行很好的逼近，在时域与频域上的局部化相当明显。可以利用小波分析对神经网络模型的优点进行强化，更加适应快速变化函数与局部非线性函数的学习。

本文使用嵌入式小波神经网络对建筑物变形进行预测，选取的小波函数为Morlet函数。在使用小波神经网络进行预测前，首先使用GM(1，1)预处理数据，降低建筑物变形数据的随机波动性。将预处理后的数据作为小波神经网络模型的输入数据，期望数据为原始观测数据。使用小波神经网络模型进行试验数据的网络初始化、样本分类处理、网络训练以及权值修正后，得到最终预测值，通过预测结果分析模型的有效性与准确度。

4.3 模型预测评价指标

为了对本文提出的组合模型的有效性和可靠性进行检验，将平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、均方根误差(RMSE)、相对误差q作为模型预测结果的评价指标[9-10]，分别表示为：

(6)

(7)

(8)

(9)

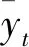
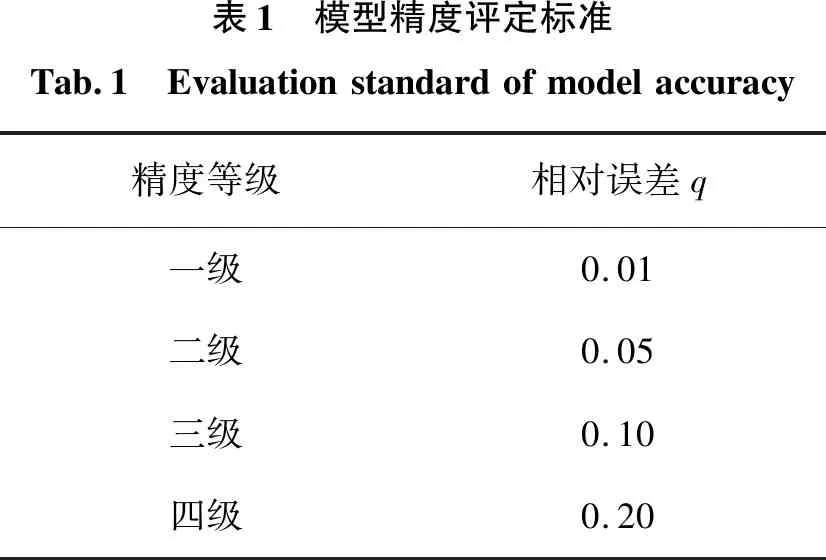
表1 模型精度评定标准Tab.1 Evaluationstandardofmodelaccuracy精度等级相对误差q一级0.01二级0.05三级0.10四级0.20

4.4 结果分析

将前24期数据作为训练样本，后6期数据作为期望值，与预测值进行对比。图2和图3分别是灰色模型，小波神经网络模型以及灰色—小波神经网络模型的预测结果对比曲线和相对误差对比曲线，表2和表3分别是三种模型的预测结果对比和精度统计。

图2 三种模型预测结果对比Fig.2 Comparison of prediction results of the three models

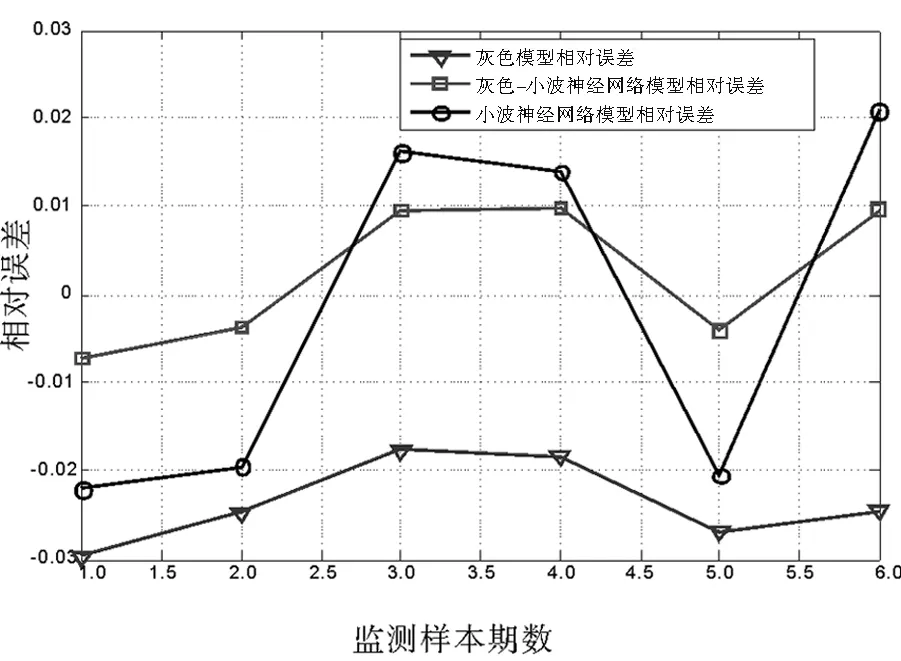
图3 三种模型预测结果相对误差Fig.3 Relative error of prediction results of the three models

从表2可以看出，灰色—小波神经网络模型的预测值与真实值更加接近，预测残差值比灰色模型预测残差更小，表现出比灰色模型、小波神经网络模型更加优越的预测效果。

表2 三种模型预测结果对比Tab.2 Comparisonofpredictionresultsofthreemodels期数实测值/mm灰色模型预测值/mm残差值/mm小波神经网络模型预测值/mm残差值/mm灰色-小波神经网络模型预测值/mm残差值/mm2533.0334.01-0.9833.76-0.7333.27-0.242634.3535.2-0.8535.02-0.6734.48-0.132735.7236.35-0.6335.140.5835.340.382836.5637.23-0.6736.050.5136.150.412938.5739.61-1.0439.36-0.7938.73-0.163039.1540.11-0.9638.330.8238.580.57

从图2可以看出，灰色模型的缺点在于随着时间的推移，预测结果偏离真实值更大，预测精度越来越低，灰色—小波神经网络模型对这种问题有了较好的改善。表3为模型预测结果精度统计。

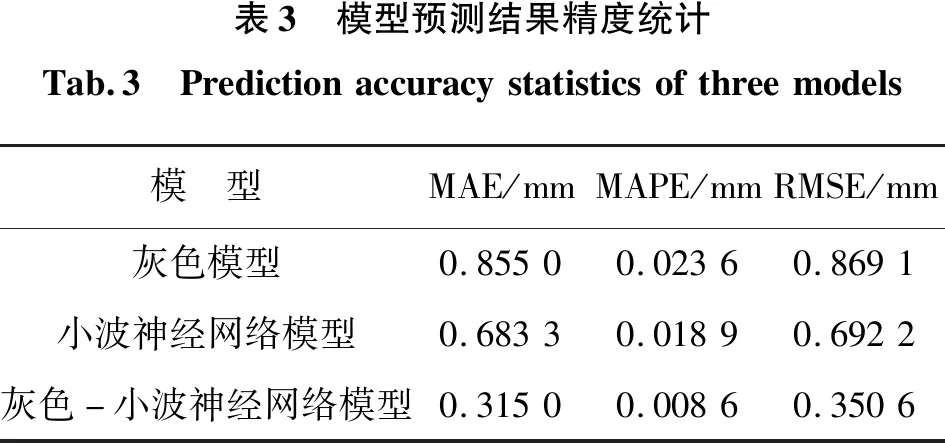
表3 模型预测结果精度统计Tab.3 Predictionaccuracystatisticsofthreemodels模 型MAE/mmMAPE/mmRMSE/mm灰色模型0.85500.02360.8691小波神经网络模型0.68330.01890.6922灰色-小波神经网络模型0.31500.00860.3506

从图3和表3可以看出，灰色—小波神经网络模型的相对残差都在-0.01～0.01之间，符合一级精度的要求。对于非线性数据的整体预测精度来说，灰色—小波神经网络模型预测结果的平均绝对误差、平均绝对百分比误差、均方根误差都低于其他两种模型，预测结果更好。

通过对预测结果进行分析，结果表明，灰色—小波神经网络预测模型在对建筑物偏移数据的预测中精度更加稳定，预测准确度更高，能够更好地预测建筑物的变化趋势。

5 结束语

本文在传统预测模型的基础上提出了灰色—小波神经网络模型，并且使用建筑物变形数据对灰色—小波神经网络预测模型与灰色预测模型和小波神经网络模型预测结果进行对比。试验结果表明，三种预测模型预测结果与真实观测值相近，但是相比于灰色预测模型与小波神经网络模型，灰色—小波神经网络模型的预测精度与稳定性更高。灰色—小波神经网络模型预测结果的相对残差在-0.01～0.01之间，符合精度要求。灰色—小波神经网络预测模型更能反映建筑物变形趋势，可为建筑物变形监测提供有效参考。