地铁列车弓网接触电阻数学模型研究
2022-05-11张冬冬李小波吴竑霖
张冬冬, 李小波, 张 浩, 张 程, 吴竑霖, 汪 翔
(上海工程技术大学 城市轨道交通学院, 上海 201620)
0 引 言
弓网滑动电接触是地铁列车获取电能的途径,由受电弓和接触网组成,良好的弓网接触状态是确保城市轨道受流质量和安全运行的重要条件之一。 列车运行时,受电弓滑板与接触线之间的接触点会形成接触电阻。 弓网接触电阻对列车受流质量有较大的影响,同时也影响受电弓滑板与接触网导线的使用寿命。 接触点中有少部分绝缘膜会在击穿电压下或外力下被破坏,形成导电斑点,导电斑点中有接触电流流过,由于收缩效应形成收缩电阻,再加上表面膜电阻的和就是接触电阻。 导电斑点的大小和数目直接影响接触电阻的大小,导电斑点与接触元件的材质、接触形式、接触力、接触电流大小等因素密切相关。 弓网接触状况与接触电阻息息相关,因此,接触电阻的模型计算对改善弓网受流质量及减小磨耗有重要的意义。 陈忠华使用改进的高斯-牛顿迭代算法求解了针对接触压力、速度、接触电流的接触电阻数学模型;平宇做了波动接触力下弓网摩擦力建模研究,建立了与波动接触力和电流相关的模型;时光采用ε 不敏感支持向量机建立波动载荷、接触电流、滑动速度与接触电阻之间的预测模型,并采用假设检验的方法验证了模型的有效性;陈忠华从理论上分析了接触斑点数目的改变对电流稳定性的影响;王铁军应用多目标粒子群算法求解电流相对稳定系数和磨损率的Pareto 最优前沿解,通过基于信噪比的多目标决策方法确定基于电流稳定性相对最好、磨损率相对最小情况下的最优压力载荷;李春茂分析了不同接触压力、滑动速度、接触电流影响下弓网接触电阻变化趋势,并根据试验结果和理论分析建立了接触电阻数学模型。 目前的研究成果多着眼于电气化铁路,对地铁列车的研究较少,地铁列车与电气化铁路在供电制式、电路拓扑等方面具有很大的不同,本文基于城轨交通受电弓试验台测得的数据,通过理论分析建立了符合地铁运行工况的接触电阻数学模型,对增强地铁列车受流可靠性具有重要的参考价值。
1 弓网接触试验台与材料
1.1 试验台
本文利用城市轨道交通受电弓试验系统进行数据采集,如图1 所示。 受电弓在车辆运行过程中有弓网间的纵向运动、接触导线的“Z”字形运动、受电弓底座的垂向振动。 纵向运动用一个大直径的圆盘来模拟,圆盘可以旋转,接触网线和弓头间的弹性接触,通过弹性悬挂方式模拟,旋转圆盘运动时通过气缸推动在导轨上往复运动,模拟“Z”字形运动。
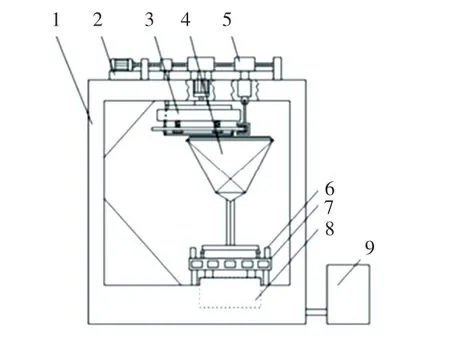
图1 受电弓试验台Fig.1 Pantograph test bench
试验台将380 V 三相交流电通过变压器和整流器变换为50 V 的直流电,输送给受电弓,利用一个电阻箱模拟车辆负载,如图2 所示。 为了控制运行和采集性能参数,本系统设置了一套工业计算机和多功能数据采集卡组成的测控系统。 接触电流、接触电压通过回路里的电压、电流传感器测量,压力通过安装在受电弓两个滑板两端的压力传感器测得,弓网接触压力通过计算其合力得到,接触电阻通过伏安法计算得到。

图2 受电弓试验台供电和受流系统Fig.2 Power supply and current collection system of pantographtest bench
1.2 试验材料
试验中使用的碳滑板参数,见表1;铜锡接触线参数见表2。
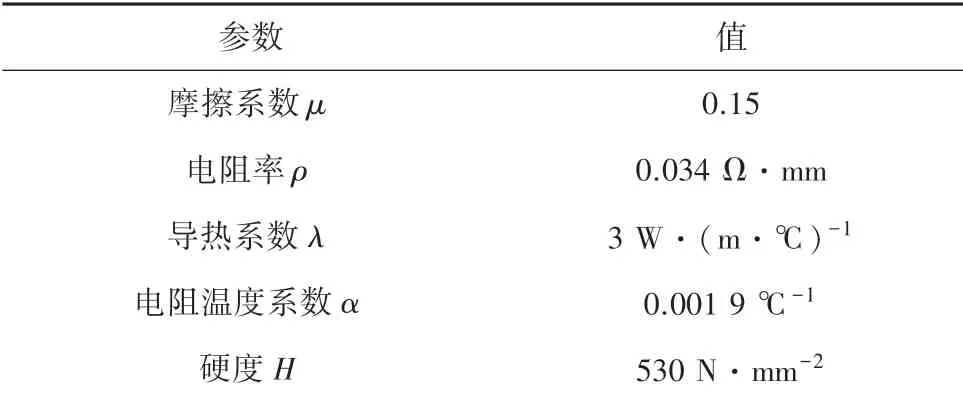
表1 碳滑板参数Tab.1 Carbon skateboard parameters

表2 铜锡接触线参数Tab.2 Copper tin contact wire parameters
2 试验结果与分析
2.1 接触压力对接触电阻的影响
当接触电流为80 A,速度分别为5.55 m/s、8.33 m/s、11.11 m/s 时,得到接触电阻在接触压力为60~120 N 范围内的变化曲线如图3 所示。 由图3 可知,滑动速度与接触电流不变时,接触电阻随接触压力的增大而逐渐减小,且接触电阻减小趋势逐渐降低。
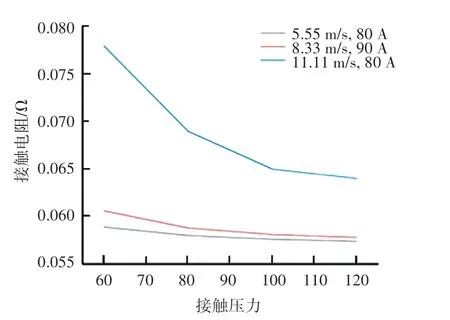
图3 接触电阻随接触压力变化曲线Fig.3 Variation curve of contact resistance with contact pressure
根据赫兹弹性接触理论,弓网接触的本质是接触面粗糙不平,形成的微凸峰的接触,受到的压力较小时,微凸峰个数也较少,且接触压力不足以将大部分表面膜压破,导电斑点难以形成,阻碍了接触电流通过,接触电阻较大;随着接触压力增大,接触面上较大的微凸峰产生弹性形变,此时较小的微凸峰得以接触且表面膜被压破,导电斑点数目增大,接触电阻减小;压力继续增大,较大的微凸峰逐渐在压力作用下形成塑性形变,接触面上不再产生新的接触点,且随着接触面积增大,总压力不再变化,导致每个接触点的压强减小,接触面被刺破的可能性减小,导电斑点数目趋于固定,所以接触电阻的减小会趋于一个稳定值。
2.2 滑动速度对接触电阻的影响
当接触电流为70 A,接触压力分别为80 N、100 N;接触电流为80 A,接触压力为100 N 时,得到接触电阻随滑动速度在5.55 ~11.11 m/s 之间的变化曲线,如图4 所示。 由图4 可知:保持接触电流和接触压力不变时,接触电阻均随车辆滑动速度的增大而增大。
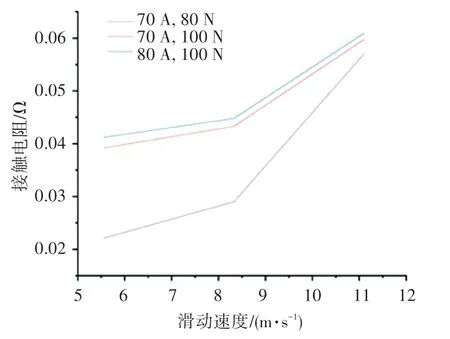
图4 接触电阻随滑动速度变化曲线Fig.4 Change curve of contact resistance with sliding speed
地铁列车运行过程中速度加快,弓网之间接触逐渐变得不稳定,导致部分导电斑点消失,从而引起接触电阻的增大;随着车辆滑动运行,弓网间机械摩擦会产生大量热量,使接触材料变软,导电斑点接触面积增大,从而引起接触电阻减小;随着接触不稳定,弓网间产生电弧现象,对接触面材料造成侵蚀,破坏接触表面,引起接触电阻增大。 综合以上分析,热量引起的接触电阻减小相对另外两点影响较小,所以总体呈现出接触电阻随滑动速度增大而增大的趋势。
2.3 接触电流对接触电阻的影响
当滑动速度为8.33 m/s,接触压力分别为80 N、100 N、120 N 时,得到接触电阻随接触电流在60~100 A 之间的变化曲线,如图5 所示。 由图5 可知,保持滑动速度和接触压力不变,随接触电流增大,接触电阻减小,当接触电流达到90 A 以上后,接触电阻几乎稳定。
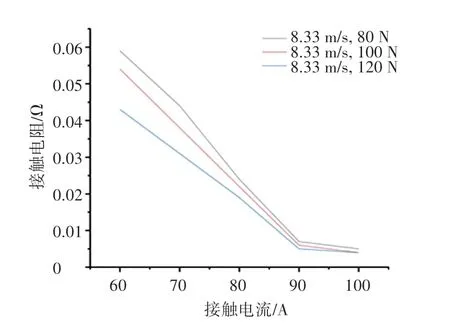
图5 接触电阻随接触电流变化曲线Fig.5 Change curve of contact resistance with contact current
接触电流通过接触面时,会产生大量热量,引起接触面硬度的下降,导致导电斑点的半径、形状等变大,具体表现就是接触电阻减小。 同时,随着接触电流增大,在接触表面会形成一层导电性较差的氧化膜,影响了导电斑点的导电性能,导致接触电阻整体变化趋势是减小的。 与此同时,接触电流产生大量的热量,接触面温度会上升,导致接触电阻减小受到阻碍,减小趋势变缓,所以在接触电流达到90A 后,接触电阻几乎不再减小。
3 接触电阻模型的建立与验证
3.1 模型的建立
3.1.1 接触电阻关于接触压力的模型
单个导电斑点接触电阻可用公式(1)计算:
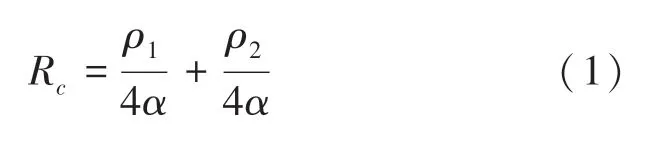
其中,R是单个接触点的电阻;、分别为两个接触面材料电阻率;为接触点半径。
假设有个接触点,且接触点半径都相同,可以得到个接触点的接触电阻,式(2):

接触面半径与接触压力之间的关系可由赫兹公式(3)导出:
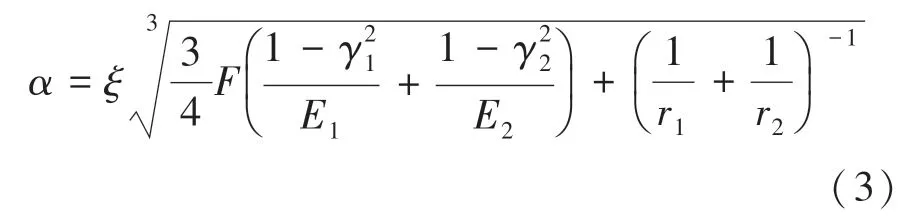
其中,为压力;为接触斑点泊松比;为接触斑点弹性模量;为接触点半径;为01 之间的一个修正系数。 整理式(2)、式(3) 得式(4):
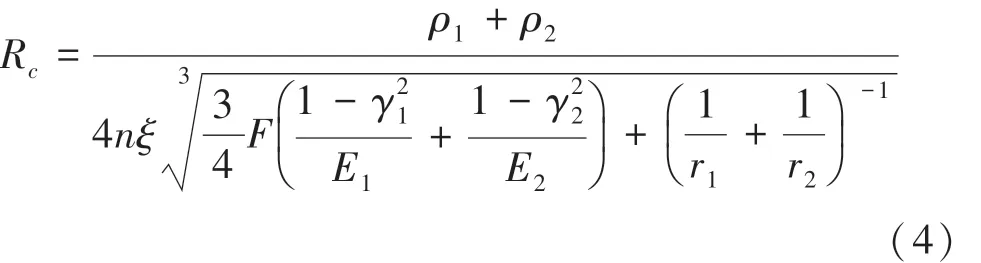
由于泊松比、弹性模量、电阻率、接触点半径都属于常量,所以式(4)可化简为式(5):

其中,、为未知参数,为接触压力,单位为N。 由于接触电阻受压力影响变化最终会趋于一个稳定值,则接触压力非常大的时候,摩擦副体电阻就是接触电阻,此时收缩电阻为0。 因此,考虑在式(5) 中添加一个修正系数,式(6):

3.1.2 接触电阻关于接触电流的模型
已知带表面膜的接触电阻可以表示为式(7):

其中,为未知参数,为接触面温升。
由电位-温度理论可知:导电斑点的接触温升与接触电流有简单的近似二次函数关系。 所以式(7)转换为式(8):

其中,为未知参数。
结合式(6)和式(8)可得弓网接触电阻关于接触压力与接触电流的模型R,式(9):

3.1.3 接触电阻关于滑动速度的模型
由于接触电阻随滑动电流变化呈指数性增大,且增大趋势不受其他因素影响,所以得出接触电阻关于滑动速度的表达式(10):

其中,为车辆运行速度;R为静态接触电阻,与接触电流和接触压力大小有关;为未知参数。
结合式(9)和式(10)可知,无论速度如何变化,接触电阻都会随接触电流的增大而趋近于0。 由于接触电阻随接触电流增大而趋近于多个不同值,速度越大,这几个值之间的差距就越大,因此在式(10)后加一个关于速度的多项式来进行修正,式(11):
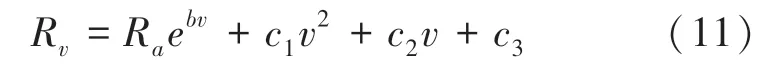
其中,、、为未知参数。
结合式(9)~式(11)可得式(12):
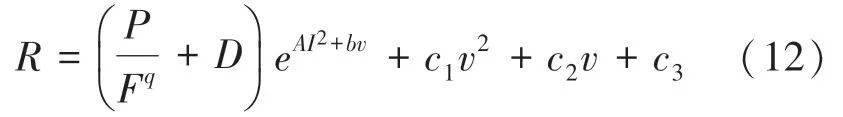
其中,为未知参数,且。
公式(12)即接触压力、接触电流、滑动速度三因素影响下的弓网接触电阻数学模型。其中、、、、、、、为未知参数,、、为单位为、、的自变量。
3.2 模型的求解与验证
确定弓网接触电阻的数学模型后,利用试验数据对模型的未知参数进行估计,以验证模型的准确性和有效性。 本文使用1stOpt 软件对试验中包含接触压力、接触电流和滑动速度3 个因素的64 组数据点进行非线性拟合。 该软件使用麦夸特法(Levenberg-Marquardt)和通用全局优化算法(UGO)相结合的迭代算法,实现非线性方程组的求解,特点为全局寻优能力极佳,可以极快地给出最优解,提高求解效率,克服了其他迭代算法必须给出初始值的难题。 表3 为未知参数最优解输出结果。
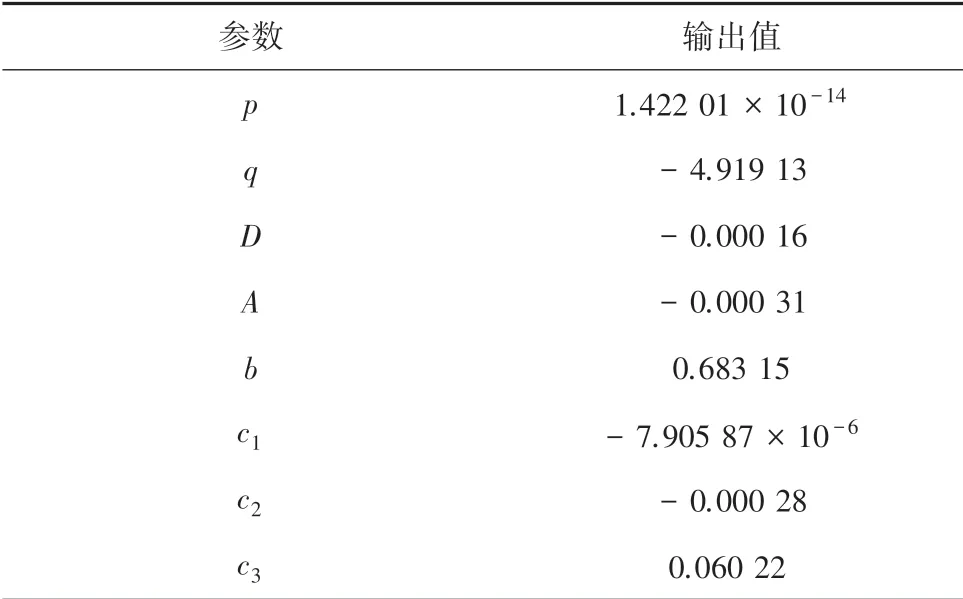
表3 未知参数最优解输出结果Tab.3 Unknown parameter optimal solution output result
将所求参数代入式(12)得式(13):
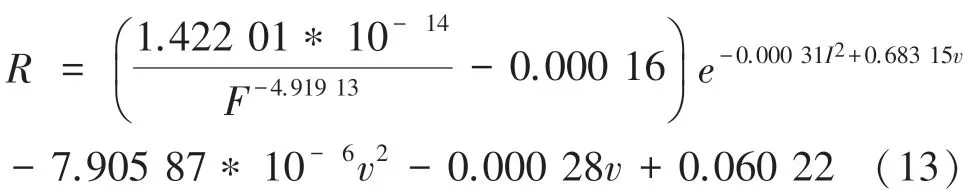
式(13)即为本文所求得的弓网接触电阻数学模型。
为了验证模型的有效性,另外选取48 组试验数据,将这48 个点与相对应的模型计算值比较,如图6 所示。 由图6 可知,模型计算值基本分布在试验测试值附近,两者吻合度较高,数值上相差不超过0.02 Ω,且试验值和模型计算值的变化基本趋于一致,说明本文建立的弓网接触电阻模型是有效的。
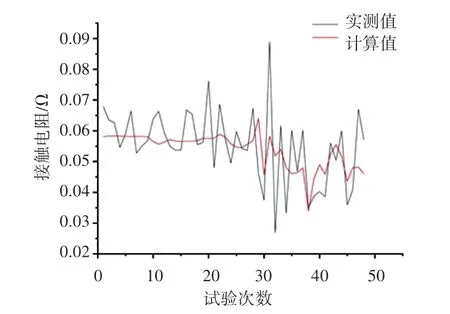
图6 试验值与模型计算值对比Fig.6 Comparison of test value and calculated value with model
4 结束语
本文通过试验数据和理论分析,建立了接触压力、接触电流、滑动速度三因素影响下的地铁列车弓网接触电阻数学模型,并验证了模型的有效性。 通过分析得出如下结论:
(1)当接触电流和滑动速度不变时,由于接触压力导致导电斑点弹性形变,使接触面积增大,接触压力在60 ~120 N 范围内,接触电阻随接触压力的增大而减小;
(2)当接触压力和接触电流不变时,滑动速度的增大导致部分导电斑点消失,并且产生电弧,滑动速度在5.55~11.11 m/s 范围内,接触电阻随滑动速度增大而增大;
(3)当接触压力和滑动速度不变时,接触电流的增大产生大量热量,导致接触面积增大,接触电流在60 ~100 A 范围内,接触电阻随接触电流的增大而减小。
本文的结论为减少地铁离线现象、增强受流稳定性与可靠性提供了重要参考。
