改进适应度函数的CMA－ES 算法在机器人逆运动学中的应用

谭薪兴， 李 光， 薛晨慷， 易 静， 于权伟

（湖南工业大学 机械工程学院， 湖南 株洲 412007）

0 引 言

机器人运动学包括正向运动学和逆向运动学，正向运动学是由一组关节角度确定机器人末端执行器一个姿态，逆向运动学是由目标姿态求解各关节角度，逆向运动学求解复杂且存在多解。

机器人逆向运动学求解是进行机器人轨迹规划、路径规划、避障等研究的基础。 很多学者在该领域做了大量研究，有许多逆向运动学的求解理论和方法，传统的方法有代数法、几何法、数值法等。代数法主要以消元的方式将高维方程组转化为低维方程组，还需要大量的三角代换，计算过程十分复杂，文献［1］提出基于分离重构技术，降低了求解复杂度，得到了逆运动学全部解；几何法针对机器人的特殊结构进行简化再求解，一般无法单独使用甚至无法使用；数值法可以精确搜索到一组逆解，求解速度与初始值相关，甚至存在无解，需要的运算量大，不适合实时性要求较高的场合。

近年来，利用智能算法求解机器人逆向运动学的方法取得一定的成果。 神经网络算法的计算代价高，计算能力很大程度取决于数据的大小，同时也取决于网络的深度和复杂程度；遗传算法全局搜索能力强，局部搜索能力较弱，容易误入局部最优解；蚁群算法和鱼群算法参数设置复杂，如果参数设置不当，容易偏离最优解；粒子群算法操作简单，收敛速度快，在众多领域得到广泛应用，但存在提前收敛、维数灾难等问题。

自适应协方差矩阵进化策略（Covariance MatrixAdaptation Evolution Strategy， CMA－ES）是在进化策略（Evolution Strategy ，ES）算法的基础上发展而来的无约束优化算法，在全局优化、多峰优化、多目标优化、大规模优化和结构性工程等领域得到了大量应用，该算法的搜索性能较高，并且能够达到比较高的搜索精度。 文献［6］提出了改进的CMA－ES 算法，在保留原算法的优点上，可以实时且高精度地求出逆向运动学解；文献［7］引入1／5 成功理论，调整CMA－ES 算法的规模和步长，提高了算法求解效率；上述智能算法提高了机器人逆向运动学求解的效率，但是忽略了机器人在实际运动过程中的平稳性和能耗。

本文提出了一种新的适应度函数用于CMA－ES算法求逆运动学解：与原算法相比，该算法将各关节运动范围作为约束条件，通过加权最小二乘法和位姿误差建立新的适应度函数，求解出唯一的一组运动学逆解。 将该算法应用于REBot－V－6R－6500 型六自由度机器人，仿真结果表明，该方法可以得到机器人高精度和平稳的逆运动学解。

1 CMA－ES 算法

1.1 算法原理

CMA－ES 算法是一种进化策略类算法。 经典ES 算法寻找最优解主要依靠突变，但是如何调整突变的方向没有成熟的理论支撑，需要依据经验设置，因此该方法会导致无效的突变。 为克服经典ES 的不足，CMA－ES 采用正态分布（，） 生成一定数量的搜索种群，（，） 表示搜索分布均值为，以协方差矩阵为的多元正态分布，且，其中，的列向量由的特征向量正交基组成，为 对角矩阵，化简多元正态分布（，） 得式（1）。

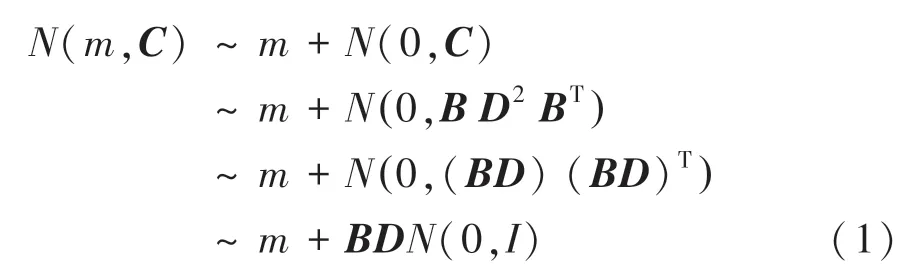
其中，“～”表示服从相同的分布。

由式（1）的逆序可知，确定等概率密度圆球面，通过、的变化可以确定的椭球面；球面的分布尺度由中的对角元素决定，主轴的方向由确定，变化、实现球面的分布旋转。

1.2 算法步骤

CAM－ES 算法流程如图1 所示。

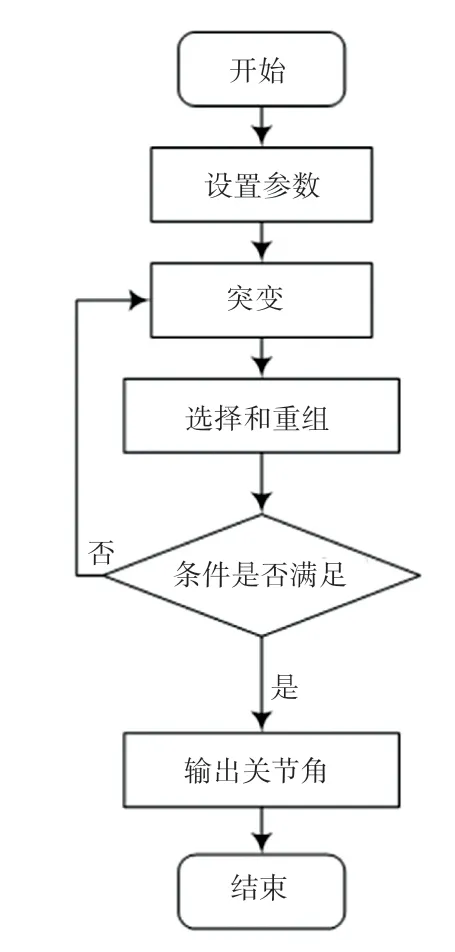
图1 CAM－ES 算法流程图Fig.1 CAM－ES algorithm flow chart

突变。 突变的目的是使个体之间产生差异，CMA－ES 算法的突变过程是以当代的均值为中心，产生下一代种群，式（2）。

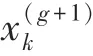
选择和重组。 经典ES 算法的选择策略有两种：一种是（） 策略，适应度排名由上一代的父代与当前子代一起参与，同时选择优秀的个体；另一种是（，） 策略，即父代不参与当前代的适应度排名竞争，优秀个体只从当前子代中选择。 CMA －ES 采用的是第二种选择策略，对个子代进行适应度评价，根据适应能力由高到低排序，选取适应能力强的前个个体，作为下一代种群的父代，更新策略参数、、，以此来传递优良的基因。

（1） 均值移动：下一代起始搜索点，即新的均值是从样本，…，中选择出来的个最优子群的加权平均值，式（3） 和式（4）。

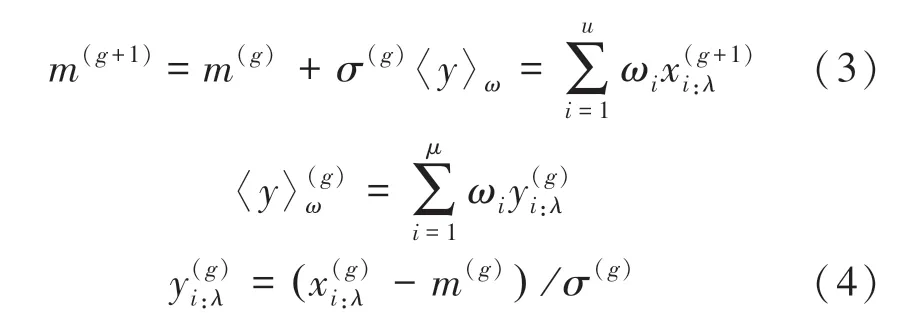
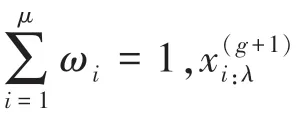
（2）协方差矩阵自适应调整（CMA），式（5） ～式（9）。

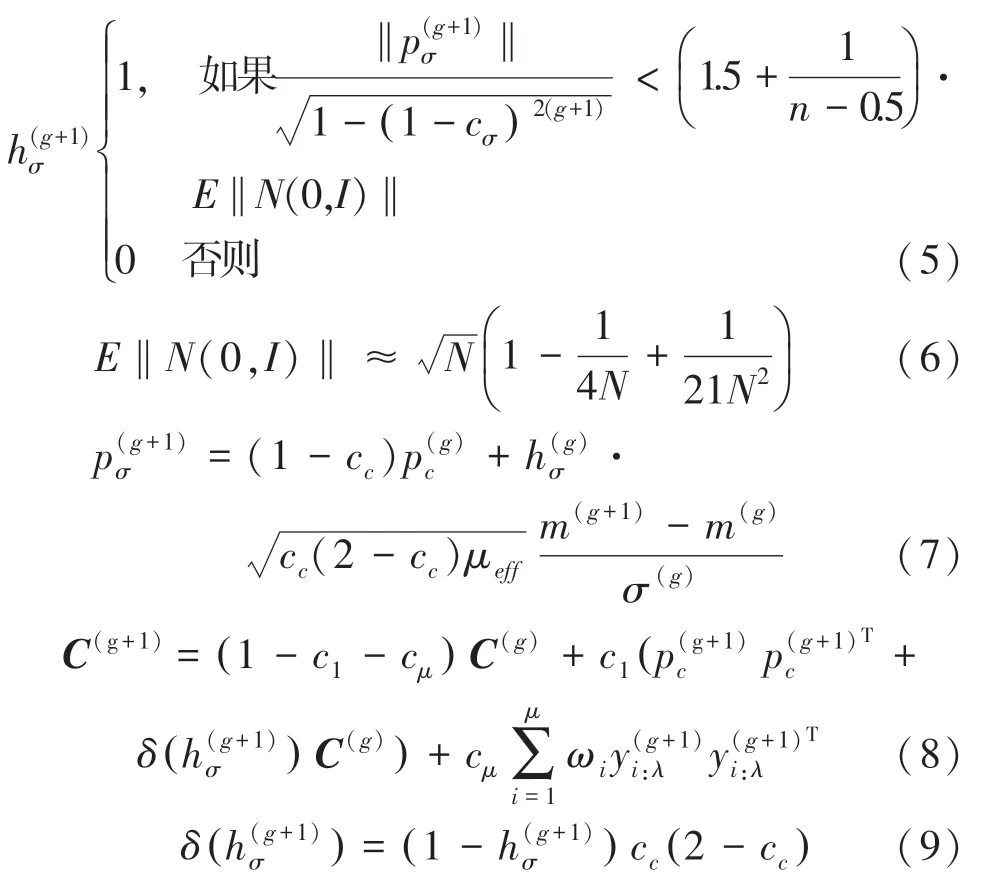
其中，c是p的更新学习速率；h为赫维赛德阶跃（）函数，用于调整‖p的过大增长；μ为方差有效选择质量，且1 ＜μ≤，和c分别为的“秩1” 和“秩” 的更新学习速率。

（3）全局步长控制（CSA），式（10）和式（11）。

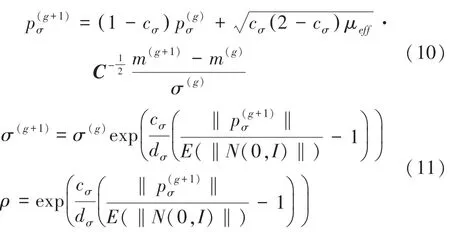
其中，可看作步长变化的伸缩因子；c为p的更新学习率；d为接近于1 的阻尼系数；‖（0，）‖为归一化进化路径在随机选择下的期望长度。

判断是否达到最大迭代次数或精度，若是，则停止，输出最优解和最优决策向量，否则返回Step 2。

2 逆运动学计算

2.1 正向运动学数学模型

采用标准D－H 法建立的REBot－V－6R－6500型六自由度机器人结构简图，如图2 所示。 目前，普遍认为D－H 法是对机器人运动学建模最好的方法，可以确定机器人的关节参数和关节变量，与机器人结构顺序和复杂程度无关，通过齐次变换矩阵描述两个相邻坐标系间的空间位姿关系。

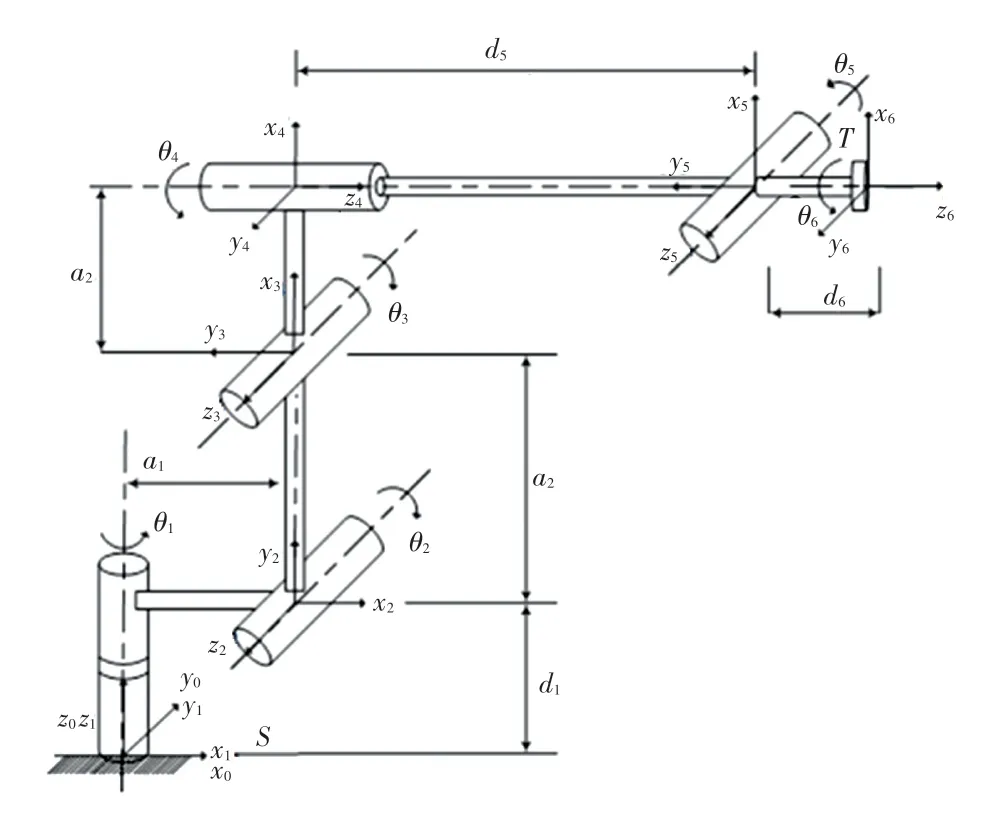
图2 REBot－V－6R－6500 结构简图Fig.2 Structure diagram of REBot－V－6R－6500

首先，建立连杆坐标系，通过4 次旋转平移变换，根据DH 参数，第连杆的参数定义为： a为连杆长度；α为相邻两关节轴线的夹角；d为第根连杆和第1 连杆的偏置距离；θ为第连杆的旋转角。 变换过程：绕z 轴旋转θ角，沿z 轴平移d，沿x轴平移a， 绕x轴旋转α，可以得到机器人连杆坐标系相对于连杆1 坐标系的变换矩阵（矩阵）即式（12）， REBot－V－6R－6500 机器人关节参数，见表1。

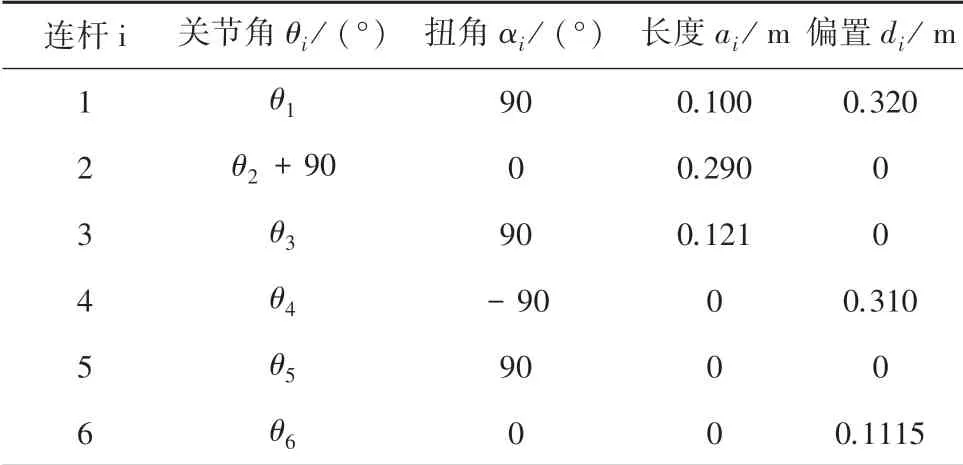
表1 REBot－V－6R－6500 机器人关节参数Tab.1 Joint parameters of REBot－V－6R－6500 robot

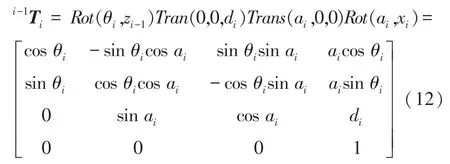
根据式（12）和表（1）中的参数，得到该型号六自由度机器人正向运动学数学模型式（13），通过正向运动学控制机器人末端执行器到达指定位置。

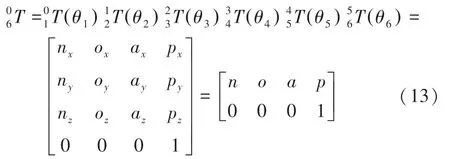
2.2 适应度函数

用机器人末端执行器的接近矢量和位置矢量建立适应度函数和，式（14）。 适应度函数为位置误差范数，表示目标位置P和实际位置P之间的误差；适应度函数为姿态误差范数，表示目标位置a和实际位置a之间的误差；适应度函数表示位置误差范数和姿态误差范数之和。 系数和是为方便调整求解过程中位置和姿态误差而设置的权重，以便求得最合适的逆解，本文中1，1。

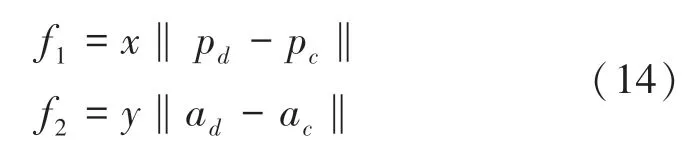
六自由度机器人逆运动学存在多解，为了获得唯一的逆解，本文基于加权最小二乘法，结合“最佳柔顺性”规则，通过附加约束建立目标函数，使用CMA－ES 算法求解适应度函数最小值，获得最优解，最佳柔顺性的含义为式（15）：

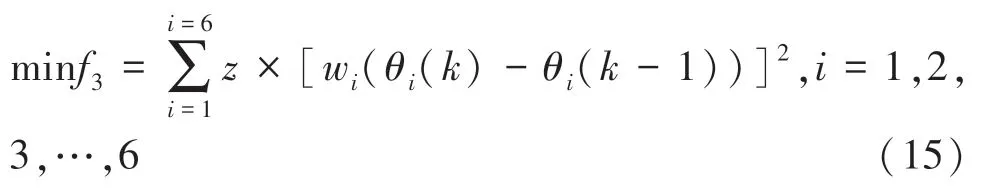
其中，θ（） －θ（1） 表示关节角与其自身前一个位置关节角的差值，使得关节运动更平滑，减少机器人运动路径距离；系数是为了保证算法运行时不产生局部收敛甚至发散等情况，平衡“最佳柔顺性”准则对整个适应度函数优化结果的影响。 本文中0.001；系数w遵循“少运动上臂，多运动下臂”的选取原则。 该原则的优点是运动时更为平稳，减少能源消耗，提高工作效率等。 在本研究中，加权系数w设计为［3 2 1.5 1 1 1］。

3 仿真与结果分析

3.1 求解工作空间

机器人的关节角取值范围参考该型号机器人说明书，见表2。 求解机器人工作空间方法有：解析法、几何法、数值法等，但这几种计算复杂、效率低，本文在机器人各关节允许的角度值限制内，以蒙特卡洛法为基础，用随机函数给各关节角赋值，得到10 000组关节角，计算机器人可达工作空间；利用正向运动学公式（13）解出末端执行器在笛卡尔空间中离散点图，从而得到机器人三维工作空间，如图3所示。

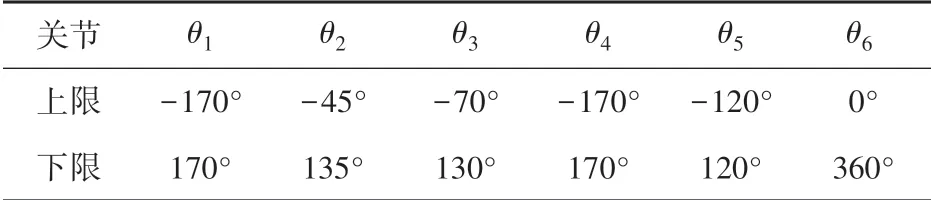
表2 关节角取值范围Tab.2 Range of joint angle

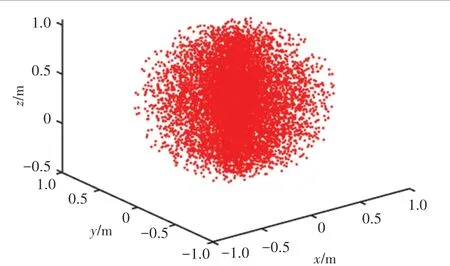
图3 三维工作空间Fig.3 Three－dimensional workspace

3.2 参数设置

CMA－ES 算法的种群数量100，优秀个体50，初始步长05，初始均值在0～1 内随机产生，求解过程中，前一个逆向运动学解作为当前初始点均值，初始均值缩放系数0.65，算法的停止条件为进化次数200 或者适应度函数≤10。为了保证算法稳定运行，两种算法的适应度函数中，权值系数1，1，0001。

3.3 点到点运动仿真

仿真的计算机配置：操作系统为64 位Window 10 企业版，处理器为AMD Ryzen 5 2600X 3.60 GHz，内存8.0 GB。

机器人初始状态时选取各关节角度为［0 0 0 0 0 0］，目标位置选取工作空间内的一组关节角，根据正向运动学公式（13）求出末端执行器的位姿矩阵， 分别使用适应度函数和， 在CMA－ES 算法上独立运行1 000 次，求逆运动学的解。 随机选取机器人的一组关节角度为［0.412 0.365 0.254 0.121 0.454 0.235］。

两种适应度函数的算法单独运行1 000 次的结果见表3，结果表明改进后适应度函数代表位置误差的适应度函数的平均值比原适应度函数中的平均值小9 个数量级；任意选取1 000 组结果中的一组的位置误差结果见表4，可以看出改进适应度函数的位置误差值比未改进的适应度函数求得的位置精度高10数量级。

表3 CMA－ES 独立运行1 000 次的适应度函数f1的值Tab.3 The value of the fitness function f1 for CMA－ES running independently for 1 000 times

表4 点对点运动位置误差Tab.4 Position error of point－to－point motion

3.4 连续轨迹跟踪仿真

在工作空间内的轨迹方程为式（16）：

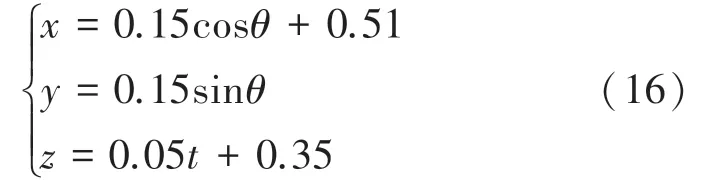
其中，0≤≤2π，步长为π／60（rad），长度单位为m，为了满足实际工作需求，保证末端执行器关节轴在工作过程中始终平行于世界坐标系轴正方向，运动轨迹的每一个点的矢量姿态均为［1；0；0］。

使用原适应度函数和改进适应度函数对选取的空间内轨迹方程（16）进行连续轨迹跟踪，适应度函数和中代表位置误差的适应度函数的结果见表5，连续求解过程中适应度函数值的波动情况如图4 所示。 仿真结果表明，改进的适应度函数中的平均值比原适应度函数中的平均值少13个数量级，同时对轨迹上所有点进行轨迹跟踪，轨迹跟踪以及轨迹仿真如图5 所示，可以看到能完全实现对给定曲线的跟踪，且运动过程平稳。

表5 连续轨迹跟踪的适应度函数f1的值Tab.5 The value of the fitness function f1 for continuous trajectory tracking

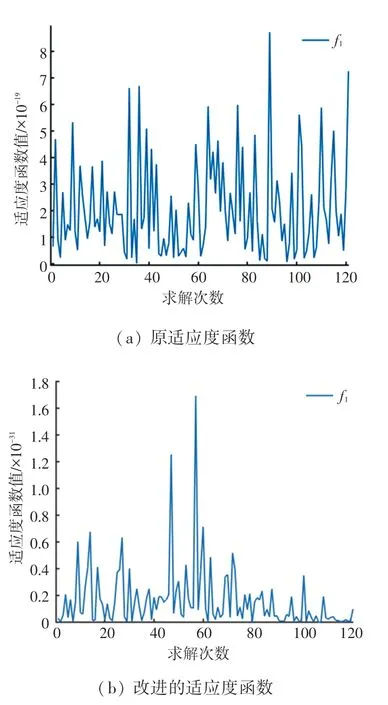
图4 适应度函数f1的波动Fig.4 Fluctuation of fitness function f1

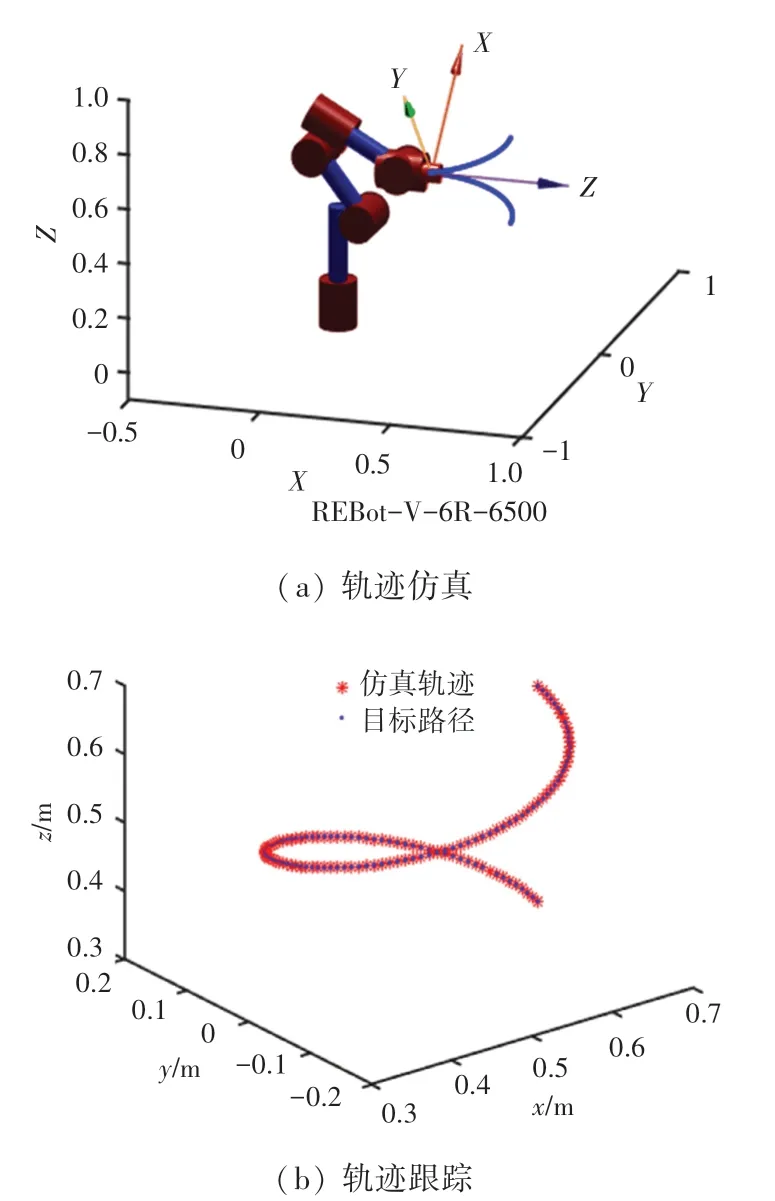
图5 轨迹仿真与跟踪Fig.5 Trajectory simulation and tracking

两种适应度函数使用CMA－ES 算法求解轨迹的关节角度变化如图6 所示。 结果表明，在保持原适应度函数的特点上，基于加权最小二乘法“最佳柔顺性”规则改进的适应度函数求解的结果唯一且更光滑，关节运动距离更小，能源消耗更少，运行过程平稳。

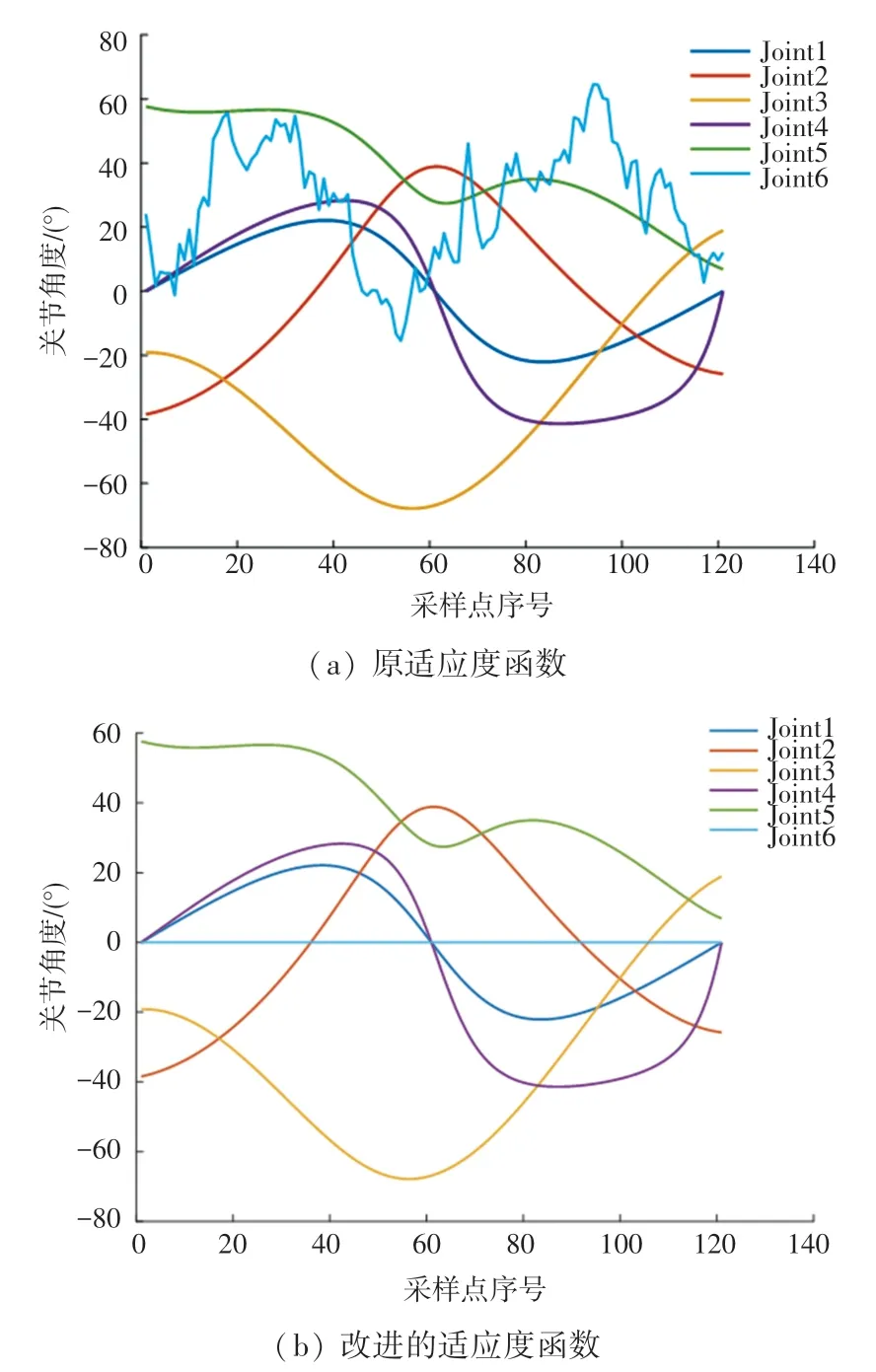
图6 关节角变化Fig.6 Changes of joint angle

在两种适应度函数求解下，笛卡尔空间中目标位置（，，） 和仿真位置（，，） 之间的误差变化，如表6、表7 和图7 表示。 可以看出，两者求解的位置精度相差较大，采用新适应度函数求解得到的平均位置误差值稳定在10m 数量级，最小值误差为0 m，且代表位置误差稳定度的标准差值也稳定在10m 数量级，在轨迹跟踪精度和轨迹跟踪稳定度方面明显优于使用原适应度函数解得的结果。

表6 原适应度函数轨迹跟踪的位置误差Tab.6 Position error of original fitness function for trajectory tracking

表7 改进适应度函数轨迹跟踪的位置误差Tab.7 Position error of improved fitness function for trajectory tracking

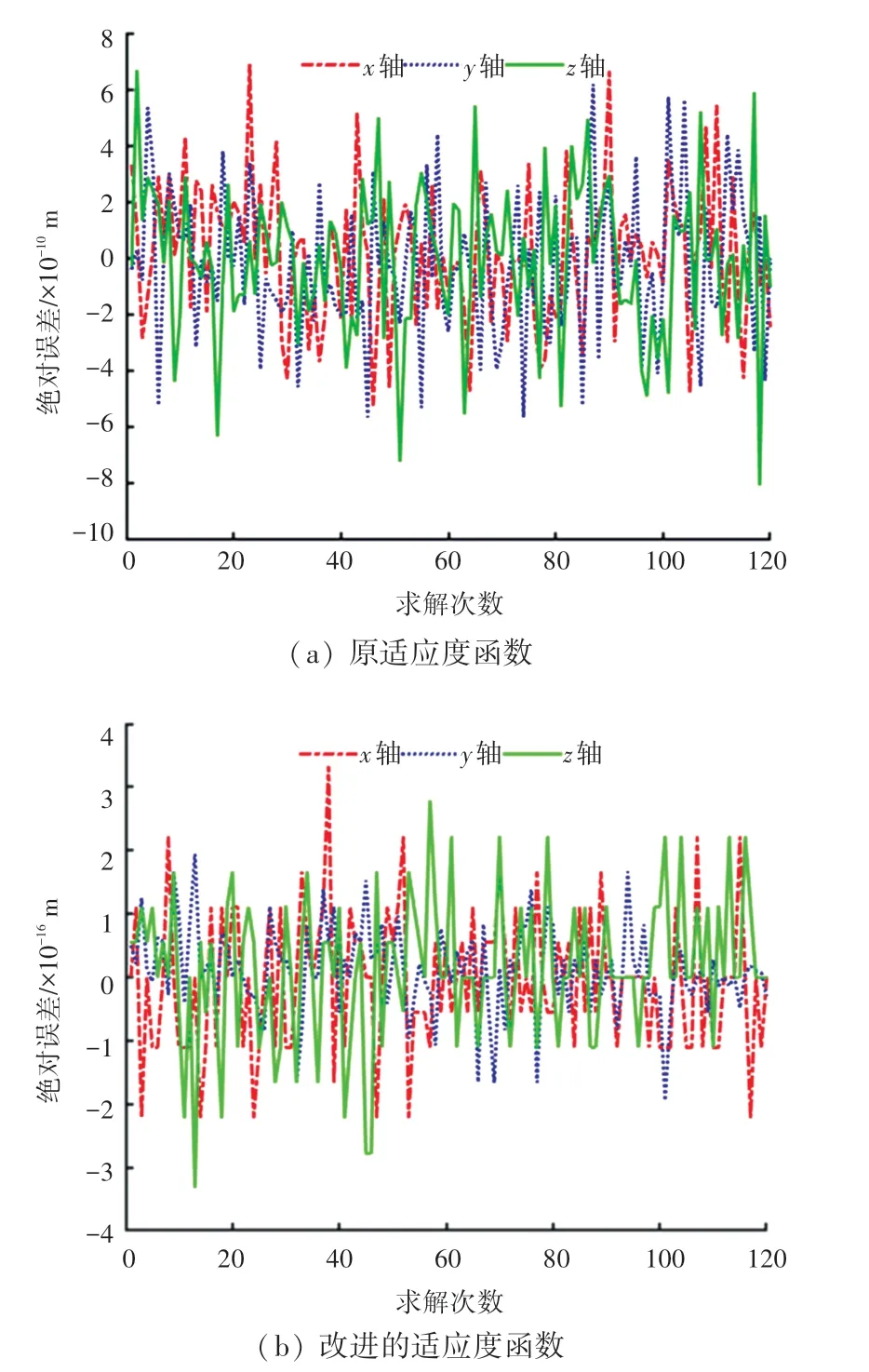
图7 空间位置误差波动Fig.7 Fluctuation of spatial position error

4 结束语

本文提出改进的适应度函数，将加权最小二乘法的“最佳柔顺性”规则和位姿误差结合，形成改进的适应度函数，使用CMA－ES 算法求逆运动学解，使其解具有唯一性；在单点求得的逆解中， 改进适应度函数中代表位置误差的适应度函数的平均值比原适应度函数中的平均值少10 个数量级；在连续的轨迹求解中，改进适应度函数中的平均值比原适应度函数逆解的结果提升13 个数量级，且使用改进适应度函数求解得到的平均位置误差值稳定在10m。

基于CMA－ES 算法将机器人关节角范围作为算法约束条件，改进的适应度函数求解精度更高，且解出的各关节角位移平滑，路径更短，遵循“多运动下臂，少运动上臂” 的原则，使得机器人能耗最少，提高了工业机器人工作效率。