基于空间线性投影的连续碰撞检测算法

万 燕， 符亚玲， 姚 砺

（东华大学 计算机科学与技术学院， 上海 201620）

0 引 言

随着计算机仿真的发展，碰撞检测作为其中最重要的环节之一，也受到了计算机图形学研究人员的极大关注。 近年来，研究人员在碰撞检测领域提出了各种有效的算法，并开发了相应的软件包，但是由于复杂的高精度模型往往包含数以万计的三角面，要在短时间内检测碰撞信息是一项极具挑战性的工作。

目前，大部分实时性较好的碰撞检测算法都是传统的离散碰撞检测算法，只在离散的时间点上对目标进行碰撞检测，这类算法可能会造成碰撞缺失，因此形成隧道效应，不仅使得场景缺乏真实感，而且会有过大的计算开销。 有研究者提出一种连续碰撞算法，在两个离散时间点之间使用线性插值的方法来描述物体运动轨迹，检查两个时间点间是否发生碰撞，同时计算首次碰撞时间。 碰撞丢失等让场景产生不真实感的问题在仿真系统中需要尽量避免，因此必须采用连续碰撞检测而不是离散碰撞检测以避免出现假象。

在碰撞检测中，碰撞目标由大量三角基元构成，一对三角对的碰撞检测可转化为9 对点面（） 基本碰撞测试和6 对边边（） 基本碰撞测试，这15对基本测试最终转换为求解三阶代数方程的问题。 求解三阶代数方程代价较大，因此对碰撞基元进行快速剔除，避免后续的求解方程是很有必要的，目前普遍采用两级碰撞算法对三角对进行剔除，即高层剔除阶段和低层剔除阶段，大大减少求解方程的数量。 经过两层剔除后，再对剩下的相对较少的基本图元对进行精确碰撞检测。 由于精确碰撞检测花费时间较多，因此尽量剔除不可能相交的基元，提高整体的碰撞检测效率。

两级碰撞检测算法仅仅规定了碰撞对需经过高层剔除与低层剔除，再执行精确碰撞检测，而两层剔除各自使用何种算法未作设定，由研究者自行设计。目前存在的低层剔除算法要么计算量大或者构造难度高，要么剔除率不高，因此，本文提出了空间线性投影滤波器（SLPF），与文献［6］中的非穿透性过滤器（DNF）相结合对基本图元进行低层剔除，可以有效提高剔除效率。

1 研究方法

本文采用两级碰撞检测算法对三角对进行剔除，快速减少大量冗余三角对。 高层剔除选择包围盒层次结构（BVH），非穿透性滤波器（DNF）与本文提出的空间线性投影滤波器（SLPF）结合作为低层剔除方法。 整体算法框架如图1 所示。

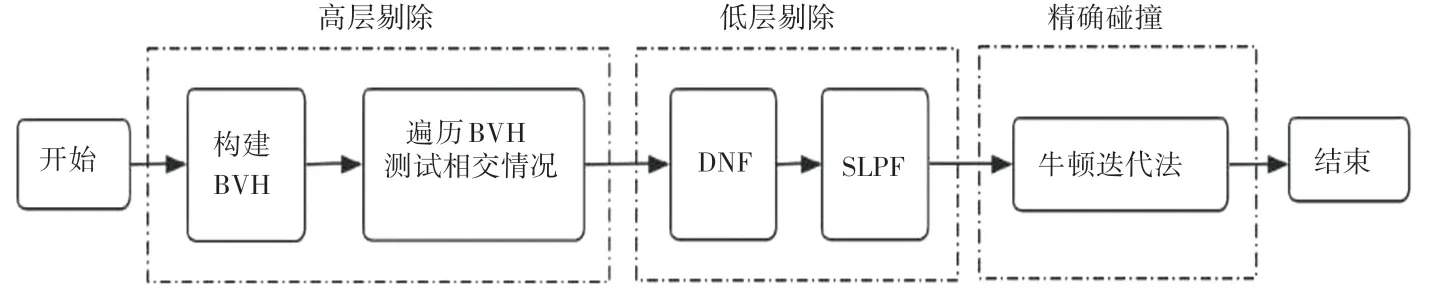
图1 整体算法框架图Fig.1 Flow chart of the proposed algorithm

1.1 高层剔除

高层剔除阶段主要是对场景中明显不相交的基元进行整体剔除，通常使用包围盒层次方法（BVH）或者空间分割法。 包围盒的种类很多，如球形包围盒、AABB 包围盒、OBB 包围盒和kDOPs 包围盒；空间分割常用的有均匀网格、二维空间分割树（BSP）和八叉树（Octree）。

本文的高层剔除选择包围盒层次结构（BVH），以包围盒（BV）作为结点的树，根结点是一个包括所有物体的包围盒，叶子结点是最小的包围盒，通常只包含一个图元，一个简单的包围盒层次结构（二叉BVH 树）如图2 所示。 不同的包围盒，其构成的BVH 剔除效果不同，在综合考虑剔除效果与时间效率后，本文选用k－DOPs 包围盒。值不同时其剔除效果也不相同，的取值有6、8、12、14、18 和26，理论上值越大剔除效果越好，树的构建和更新所耗费的时间越多，但相交测试的时间越少。 一般情况下，相交测试时间远大于构建树的时间，因此选定值为26。 此外，为了进一步提升包围盒剔除效果，本文在传统BVH 上增加了一层额外包围盒，使得包围盒最小包围的是三角形的点和边，而不是三角形本身。

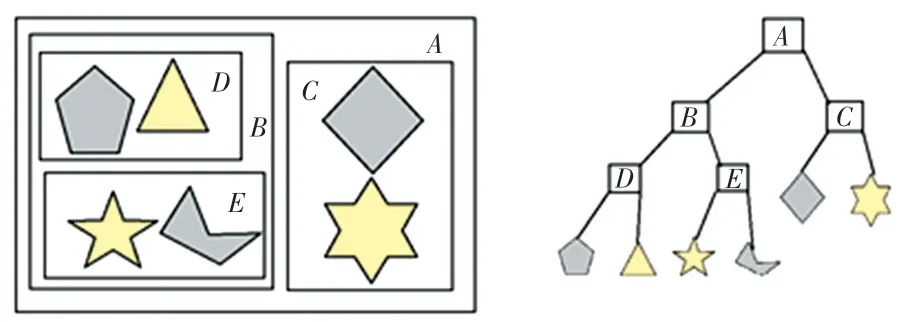
图2 简单场景二叉BVH 树Fig.2 Simple example of BVH

1.2 低层剔除

经过高层剔除，仍然有很多冗余三角面片不能被剔除，低层剔除将待检测图元对的碰撞检测转换为点面测试和边边测试，每个基本测试又可以分为两个部分：共面测试和内部测试。

以点面测试（测试点面对的碰撞情况）为例，若点和面发生碰撞，则点在△内部，即、、、4 点共面（共面条件）；同时碰撞点在△内（内部条件），如图3 所示。 判断碰撞对是否满足共面条件称为共面测试，判断碰撞对是否满足内部条件的称为内部测试。

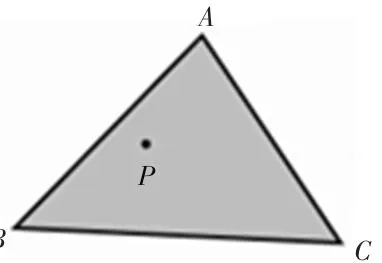
图3 点面对发生碰撞时的位置关系Fig.3 Position of VF－pair when they collide

低层剔除使用的有代表三角形、孤集和滤波器等方法。

本文的低层剔除采用两个滤波器：非穿透性滤波器（DNF）和本文提出的空间线性投影滤波器（SLPF）。 由于碰撞对确定碰撞需要满足两个条件：共面条件和内部条件。 DNF 可以剔除不满足共面条件的碰撞对，而本文提出的SLPF 可以剔除部分不满足内部条件的碰撞对，因此综合使用这两个滤波器，可以剔除大量不满足碰撞条件的碰撞对，得到效果较好的低层剔除。 在多个模型上实验证明，结合使用DNF 和SLPF 的方法比仅使用DNF 方法剔除数量更多。

2 空间线性投影滤波器

空间线性投影滤波器（SLPF）是将碰撞对投影到空间中的直线上，根据直线上投影点的位置关系，直观简单地判断碰撞对原来的位置关系，可以剔除大部分不满足内部条件的碰撞对。

2.1 符号说明

、和V分别表示点在0，1，以及任意∈［0，1］的情况。

，，，表示点面对（） 的运动点和三角形的3 个顶点，，，，表示边边对（） 的两条边，的4 个顶点。

、·和*分别表示向量叉乘、点乘以及普通乘法。

黑斜体表示向量，例如：，，。

2.2 空间线性投影滤波器的理论介绍

SLPF 是将空间中的碰撞对投影到空间中的某条直线上，根据投影点的位置关系来剔除不可能发生碰撞的碰撞对。 在点面碰撞中，若点的投影点始终在三角形3 个顶点的投影点的同一侧，则可剔除；在边边碰撞中，若一条边的两个顶点的投影点始终在另一条边的两个顶点的投影点的同一侧，则可剔除。

在任意时间间隔内，对于特定的投影空间，如果两个变形基元在投影空间中没有相交，则这两个基元在其原空间中也不会相交。

假设在原本的空间中两个变形基元相交，那么在投影空间中这两个基元也一定相交，与两个基元在投影空间不相交矛盾，故假设不成立，定理1 成立。

下面分点面对（VF－pair）和边边对（EE－pair）两种情况分别说明SLPF 的原理。

（1）点面对：将VF－pair 的4 个点，，，投影到某条直线上，记为，，，。 由定理1 可知，若整个时间间隔内没有相交，那么必定存在一条直线，有始终在、、的左边（或右边），则这一对点面一定不发生碰撞，反之则不一定发生碰撞。点面对在方向向量为（1，0，0） 即轴上的投影情况，如图4（a）所示。

（2）边边对：将EE－pair 的4 个点，，，投影到某条直线上，记为，，，。 由定理1 可知，若整个时间间隔内没有相交，那么必定存在一条直线，有、始终在、的左边（或右边），则这一对边边一定不发生碰撞，反之则不一定发生碰撞。边边对在方向向量为（1，0，0） 即轴上的投影情况，如图4（b）所示。

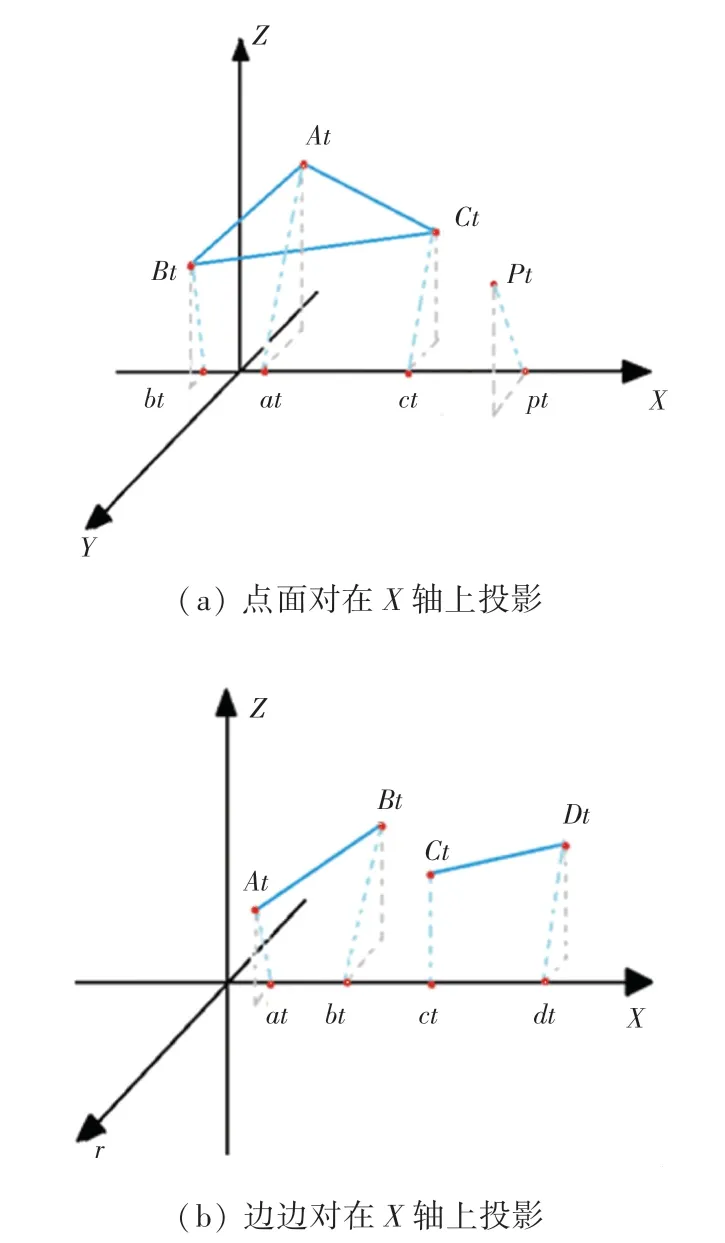
图4 碰撞对在X 轴上投影Fig.4 The projection of VF－pair and EE－pair onto the X－axis

2.3 空间线性投影滤波器计算推导

为将位置关系转换为能够用程序计算的公式，下面进行计算推导。

记投影向量的单位向量为，以点和为例。 如果的投影点一直在的投影点的右侧，则有线段构成的向量在以为单位向量的直线上的投影为与的点乘大于0，即·0一直成立，如果的投影点一直在的投影点的左侧，则·0 一直成立。

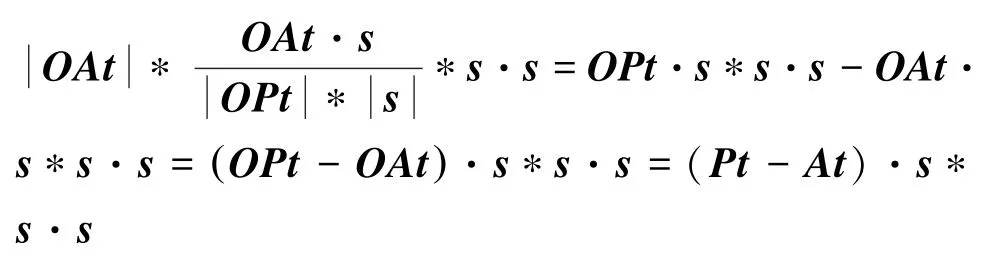
在连续碰撞检测中，有任意一点V ＝V*（1）*，因此有：

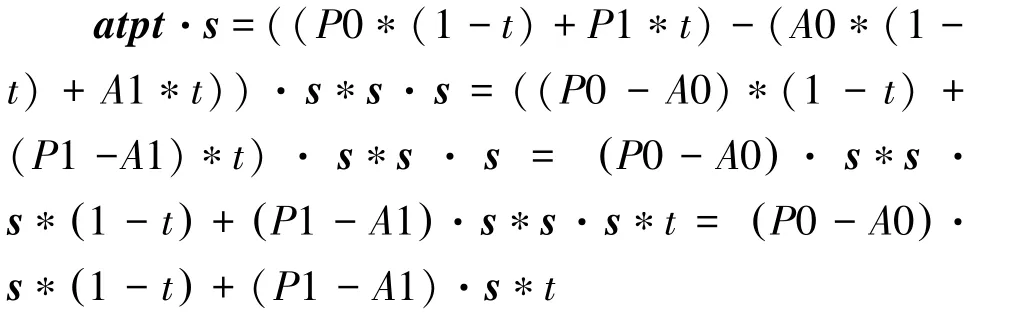
其中，0、0 表示点、在0 时刻的坐标，点1、1 表示点、在1 时刻的坐标，∈［0，1］。因此，在VF － pair 中只要满足式（1） 中1，2，3，4，5，6 同号，那么此时间间隔内不发生碰撞。

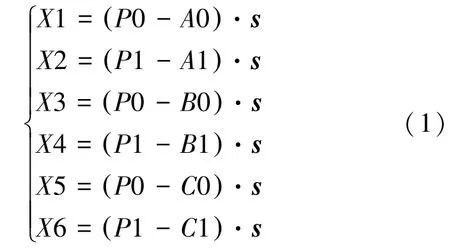
其中，0，0，0，0 表示点，，，在0时刻的坐标，点1，1，1，1 表示点，，，在1 时刻的坐标。

在EE － pair 中只要满足式（2） 中1，2，3，4，5，6，7，8 同号，那么此时间间隔内不发生碰撞。

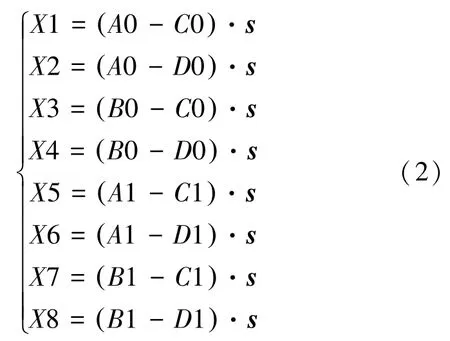
其中，0，0，0，0 表示点，，，在0时刻的坐标，点1，1，1，1 表示点，，，在1 时刻的坐标。

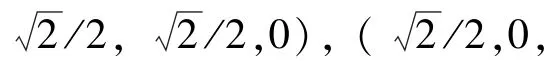
3 结果与讨论

本文实验环境为Intel Core i7－8565U CPU＠1.80 GHz 2.00 GHz，编译环境为VS2017，代码编写采用C＋＋，测试数据为funnel 和cloth＿ball 数据模型，数据来自北卡罗来纳大学教堂山分校（University of North Carolina at Chapel Hill，UNC）。funnel：9 450 个点，18 484 个三角面；cloth＿ball：46 598个点，92 230个三角面，渲染图如图5 所示。

图5 数据集渲染图Fig.5 Rendering image of dataset

3.1 确定k 值

对比不同包围盒的优劣，本文最终选择kDOPs包围盒。 为了确定适合的值，本文对为6、8、14、18、26 分别进行测试，对比不同值在funnel 和cloth＿ball 数据上一帧的剔除数量与时间，结果如图6所示。在funnel 上，为26 时无论是边边对还是点面对的剔除率都是最高的，且花费时间最短；在cloth＿ball上，为26 时无论是点面对还是边边对的剔除率都是最高的，时间稍稍长于为14 和18 时。 综合考虑花费时间与剔除数量后，本文采用26－DOPs。

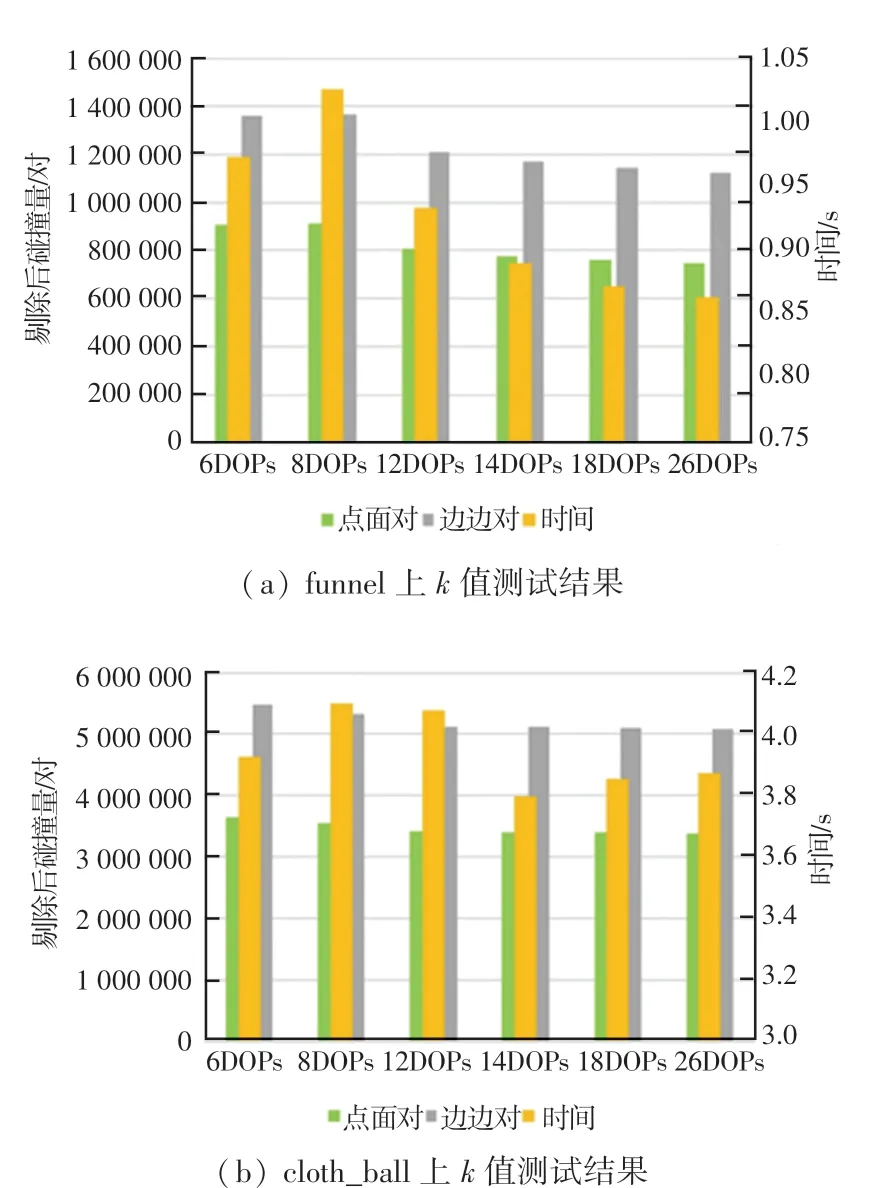
图6 k 值测试结果Fig.6 Results of the k－value test

3.2 滤波器实验

空间线性投影滤波器（SLPF）对基本测试中不满足内部条件的碰撞对进行快速剔除，为提高剔除率，又增加一个非穿透性滤波器（DNF）来进行非共面剔除。 分别在cloth＿ball 和funnel 上进行实验，经过26－DOPs 剔除后，对比仅使用SLPF、仅使用DNF以及使用SLPF＋DNF 进行剔除的效果，结果见表1和表2，其中时间为每帧时间。 可以看出，仅使用SLPF 比仅使用DNF 的剔除数量更多，使用SLPF＋DNF 的剔除数量最多。 由于SLPF＋DNF 路径是在SLPF 为真的情况下再进入DNF 判定，增加了计算，所以时间花费比只经过一层滤波器稍多。 而对于SLPF 或者DNF，不同的碰撞位置需要计算的不等式数量不同，而具体哪个滤波器需要计算的不等式数量更多无从判定，因此有时SLPF 花费的时间多，有时DNF 花费的时间多。

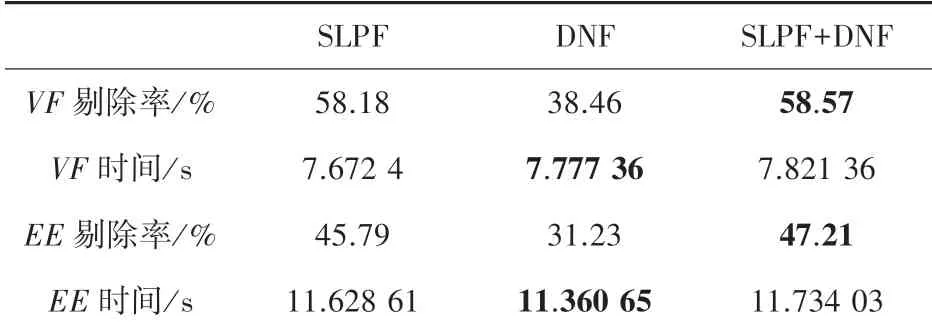
表1 cloth＿ball 上的测试结果Tab.1 Test results on cloth＿ball dataset

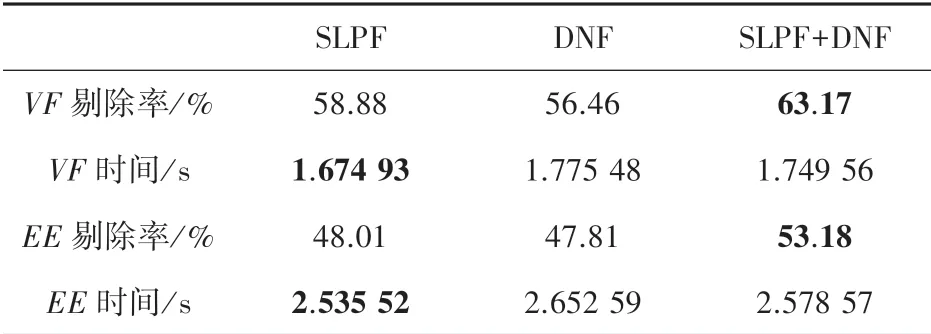
表2 funnel 上的测试结果Tab.2 Test results on funnel dataset

4 结束语

本文对连续碰撞检测算法进行研究，采用两级碰撞检测算法作为框架。 高层剔除阶段在分析各种包围盒优劣后，决定选择k－DOPs 作为包围盒层次结构的包围盒，经过实验确定值为26。 由于一对碰撞对需要满足共面条件和内部条件才能确定是发生碰撞，而已经存在的DNF 只能剔除不满足共面条件的碰撞对，于是在低层剔除阶段，提出一个可以剔除不满足内部条件的碰撞对的空间线性投影滤波器（SLPF），结合使用非穿透性滤波器（DNF），可以显著提高剔除效率。 最后，在两个数据集上进行实验，验证了这一理论。 实验结果表明，仅使用SLPF 比仅使用DNF 的剔除数量更多，使用SLPF＋DNF 的剔除数量最多。

本文算法在剔除数量上具有一定优势，但是在时间花费上并不占据绝对优势，还有改进的空间，比如：简化计算步骤。 除此之外，本文算法是基于CPU 实现的，后续可以考虑基于GPU 的并行策略来进一步减少使用时间。