基于Alpha－Beta 算法的苏拉卡尔塔棋博弈系统研究

李东轩， 胡 伟， 王静文

（沈阳工业大学 理学院， 沈阳 110870）

0 引 言

计算机博弈（Computer Games），亦称机器博弈，是一个挑战无穷、生机勃勃的研究领域。 随着人工智能的兴起，人们对计算机博弈的研究日趋深入，计算机博弈算法也已越来越多地被应用在各棋种上。

由于苏拉卡尔塔棋的棋盘比较特殊，且规则有趣，走法多变，近年来受到许多机器博弈爱好者的关注，因此本文对此进行了深入研究。

1 苏拉卡尔塔棋简介

苏拉卡尔塔是双人游戏， 源自于印尼爪哇岛的苏拉卡塔（Surakarta） 。 棋盘由6×6 正方形网络与角落上的8 个圆弧所组成，如图1 所示。 棋子在游戏开始时，双方各12 个棋子排成两行。 其游戏规则如下：

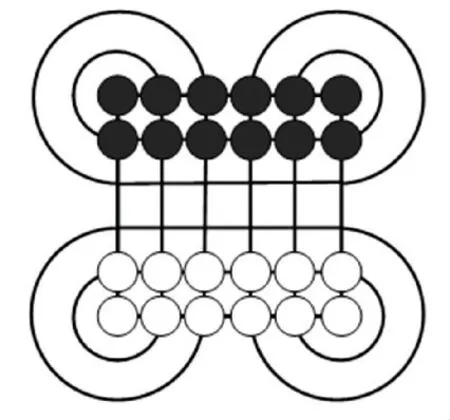
图1 苏拉卡尔塔棋棋盘Fig.1 The board of Surakarta

（1）参赛者掷硬币决定开始，每次只能移动一个棋子，双方轮流走棋；

（2）每个棋子可以向8 个方向（上、下、左、右、左上、左下、右上、右下）移动一格（所去方向无棋子）；

（3）若要吃掉对方棋子，必须经过至少一个完整的弧线，并且移动路径中不可有本方棋子阻挡；

（4）黑子可以吃掉白子，同样白子沿同一路径的相反方向也可以吃掉黑子；

（5）当一方棋子全部被吃掉时棋局结束，有剩余棋子方获胜；

（6）当双方都不能再吃掉对方棋子时，剩余棋子多的一方获胜。

2 苏拉卡尔塔棋博弈系统

苏拉卡尔塔棋博弈系统主要由可下位置的生成、估值函数、“三手进攻”算法与搜索算法相结合三部分构成。 其中，可下位置的生成需在给出当前局面时，迅速得到所有的可下位置，这与搜索算法的深度密切相关；估值函数需要准确的评估当前局面；搜索算法需要通过可下位置和估值函数，从而获得最佳下棋位置。

2.1 可下位置的生成

在苏拉卡尔塔棋博弈系统中，可下位置即棋子合法的移动位置。 通常情况，可下位置的生成方法需要遍历两边棋盘，不断地将棋子设为移动的起点和终点，并判断该走法是否合法。 该方法需要遍历两边棋盘，因此空间复杂度较高，搜索速度较慢。 由此可见，可下位置生成的速度尤为重要，关乎到搜索算法的深度及棋力。

关于生成可下位置的优化基本思路：将棋盘中本方棋子设为移动的起点，然后在轨道中寻找其可落子的位置。 具体算法如下：

棋子可移动位置分为吃子移动和不吃子移动。不吃子移动的可下位置易于实现，只需在本方棋子周围寻找即可；而吃子移动的可下位置较为繁琐。在初始化棋盘中，将内轨和外轨的位置分别存放到两个向量中；之后首先找到本方棋子，判断其在内轨道还是外轨，或者是内外轨道都在。 在内、外轨道时分为两种情况：一是在特殊点上（如图2 所示）；二是不在特殊点上。 如果棋子不在特殊点，那么在轨道向量中找到棋子的位置，分别向上或向下找到对方的棋子，再判断是否过弧而生成可下位置；如果棋子在特殊点上，棋子的位置在轨道向量中将会出现两次，分别找到这两次的位置并按上述方法生成可下位置。

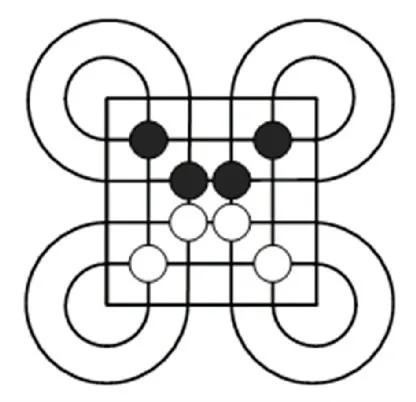
图2 特殊点位置Fig.2 Special point location

2.2 估值函数

由于苏拉卡尔塔棋最终胜负判断的方法是将对方的棋子全部吃完，或死棋时计算剩余棋子的个数，因此本文评估函数采用对盘面赋值（Value－1）与棋子数量（Value－2）相结合的策略。

2.2.1 盘面赋值（Value－1）

依据苏拉卡尔塔棋的棋盘，可见许多价值比较高的点位。 即在占领该类点位时，胜率会明显增高，故将不同位置的棋子评分，可得出各点价值对应的棋盘价值矩阵。 即：

2.2.2 棋子数量（Value－2）

棋子数量为当前下棋方的棋子个数。 一般情况下，剩余越多，优势越大。

综合考虑上述两方面，可以得出本方（黑方）总估值函数：

Value ＝Black－Value－Total－White－Value－Total

对方总估值函数White－Value－Total 同理。 最后计算出当前局面的价值：

Evalue ＝Black－Value－Total－White－value－Total

2.3 “三手进攻”开局与搜索算法相结合

苏拉卡尔塔棋中有多种开局方法，经过大量测试后，得出了先手方最优的几种进攻方式－－－“三手进攻”，如图3 所示。 所谓“三手进攻”，就是用3 步把棋盘中的外圈轨道（或内圈轨道）中的外弧（内弧）“打开”，使己方棋子在占据最优位置的同时，能够利用最快的步骤吃掉对方的棋子，并在后期内圈（外圈）轨道相互“换子”时，己方棋子会比敌方棋子多出一个，使得己方在残局时，彻底占领内圈（外圈）轨道，达到优势最大化。 己为后手方时，利用更深的搜索算法进行“防守”，当敌方中期有破绽时转守为攻。

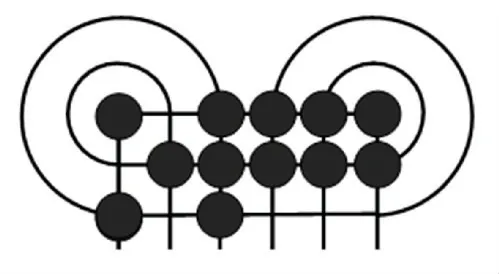
图3 三手进攻走法Fig.3 Three steps attack method

2.4 Alpha－Beta 搜索算法

目前，关于苏拉卡尔塔棋搜索效率较高的算法有Alpha－Beta 算法和UCT 算法。 但是，由于每步棋的可下位置较少，所以利用好估值函数时，Alpha－Beta 算法会更加精准。 Alpha－Beta 算法是由极大极小算法改变而来，两者的区别在于Alpha－Beta 算法可以不断的进行“剪枝”，将价值不高的局面剔除，进而提高搜索效率。 博弈系统中还使用了置换表和哈希表技术制作开局库，通过计算当前局面的哈希值，再进入开局库中查找是否存在，极大地提高了开局搜索效率。 Alpha－Beta 伪码如下：

Function Alpha－Beta（int，int alpha，int）｛

if（0‖isWin（））

return value （）

getPositions

for（i ＝1 to getPositions.size（））

makeMove（）

val ＝－Alpha－Beta（1，，－alpha）

unMakeMove（）

if（val ＞＝）

return

if（）

return

｝

3 实验与结果

针对苏拉卡尔塔棋优化后的可下位置搜索速度与普通版本（搜索层数均为7 层）搜索速度结果见表1。

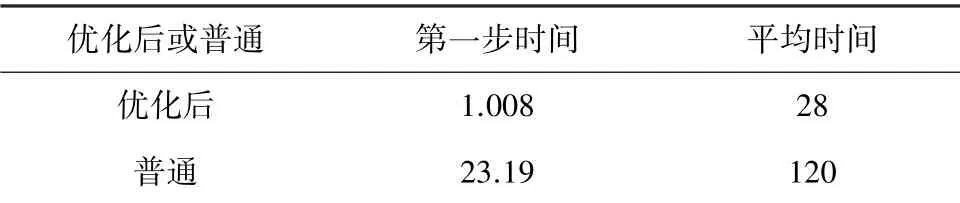
表1 生成可下位置对比结果Tab.1 Comparison of different generated downloadable location algorithm

由表1 可明显看出，运用Alpha－Beta 搜索算法搜索7 层时，优化后的可下位置生成算法相比于普通算法，可以大大减少搜索时间，极大的提高了搜索效率。

针对苏拉卡尔塔棋的估值，本文使用了棋盘估值Evalue 和Value－2，进行了Alpha－Beta 搜索算法，搜索层数为7 层时进行互相博弈比较。 比较结果见表2。

表2 不同的估值对比结果Tab.2 Comparison results of different valuations

由表2 可以看出，不同估值在同一算法下的胜率，在先后手上进行博弈时，Evalue 的估值在先后手全都取得了胜利，证明了该估值的可行性。

4 结束语

本文通过使用Alpha－Beta 搜索算法和优化后的可下位置生成算法与普通可下位置生成算法相比较，结果表明：优化后的位置生成算法在限制时间的比赛中有更好的搜索效率。 同时，在本博弈系统中加入了“三手进攻”策略和置换表与哈希表技术、迭代加深方法，并结合估值方法，极大地提高了棋力。使用本文提出的算法与策略完成的苏拉卡尔塔棋博弈程序，在2021 年全国大学生计算机博弈竞赛中取得了亚军的好成绩，再次证明了该算法的可行性。