Linex损失下Weibull分布参数的Bayes估计*

程 静，周菊玲

(新疆师范大学 数学科学学院，新疆 乌鲁木齐 830017)

0 引言

Weibull分布在可靠性分析或寿命检验中常被用到，在一些管理科学与工程领域中也有所应用，有不少学者对该分布有研究兴趣.韦莹莹等[1]讨论了Pareto分布参数在Linex损失下的Bayes估计问题，证明了所给估计是可容许的.王学敏[2]研究了Linex损失下先验分布不同时Burr分布参数的Bayes估计问题.王理峰[3]在Linex损失下得到了多元正态分布熵的最优仿射同变估计，证明了其是Bayes估计.邓立凤等[4]对逆Gaussian分布参数倒数的Bayes估计进行了研究，给出了估计并证明了该估计是可容许的.李凤等[5]在损失函数下取逐步增加的Ⅱ型截尾样本研究Weibull分布的Bayes估计.崔群法等[6]讨论了E-Weibull分布参数及可靠度在Linex 损失下的Bayes估计问题，并在该情况下对极大似然估计和Bayes估计做了对比.张丽[7]讨论了在Linex损失下各分布参数的Bayes估计及其性质，证明了所得各分布参数的估计是可容许的.王敏[8]在复合Linex损失下，参数先验分布不同时对参数的估计进行了对比，得到了参数的唯一Bayes估计.姚慧等[9，10]在Linex损失下对关于Lomax分布参数的一些Bayes估计进行了讨论.邱燕[11]对Weibull分布参数及可靠度的Bayes估计进行了研究.本文基于以上研究对Weibull分布参数的Bayes估计在Linex 损失函数下进行了讨论，给出了估计式并对其可容许性给出了证明，最后通过数值模拟验证了所得Bayes估计的稳健性和精确度.

设X是服从Weibull分布的随机变量，其密度函数为

上式中σ=ηβ,σ,β分别为尺度参数和形状参数，且σ是未知的.记X～Weib(σ,β).

(1)

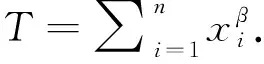
1 参数θ的Bayes估计及可容许性

定义1.1Linex损失函数的形式为

L(θ，δ)=eb(δ-θ)-b(δ-θ)-1,

(2)

式中δ,b分别为θ的估计值和该损失函数的尺度参数，b∈R且b≠0.

本文仅考虑b>0的情况，b<0情况的讨论类似.该损失函数对于δ严格凸的，且当δ=θ时有最小值.

定理1.1在损失(2)下，对任一先验分布π(θ),θ的Bayes估计为

证明设在式(2)下θ的任一估计为δ(X)，则δ(x)的Bayes风险为

E(L(θ,δ))=E{E[eb(δ-θ)-b(δ-θ)-1|X]}=

E[ebδE(e-bθ|X)-bδ+bE(θ|X)-1].

(3)

要使式(3)最小，只需极小化ebδE(e-bθ|X)-bδ+bE(θ|X)-1.令h(δ)=ebδE(e-bθ|X)-bδ+bE(θ|X)-1，对h(δ)关于δ求导并令所得导数等于零，得

因为δ是其最小值点且也是唯一的，所以θ的Bayes估计为

定理1.2在损失函数(2)下，设Gamma分布Γ(α，λ)为θ的先验分布，则θ的Bayes估计为

证明若参数θ～Γ(α,λ)，则

(4)

从而θ的后验分布

所以参数θ的Bayes估计为

引理1.1[13]在Bayes决策问题中，若对于给定的先验分布π(θ),θ的Bayes估计δB(X)是唯一的，则它是可容许的.

由引理1.1可知，如果损失函数为严格凸的，那么它的Bayes估计定是唯一的，且也是可容许的.本文所讨论的Linex损失函数与上述引理的相同，是严格凸的，因而它的Bayes估计定是唯一的，由此可得，Bayes估计是可容许的.

2 参数θ的多层Bayes估计

从上述定理1.1可以看出当参数θ的先验分布为Γ(α,λ)时，Bayes估计δB(X)中仍有超参数α,λ.因为需要进一步讨论θ的多层Bayes估计，所以此时把超参数看成相互独立的随机变量，再给出一个先验，称为超先验，进而求得θ的多层Bayes估计.当Γ(α,λ)分布的超参数λ>0,0<α<1时，α,λ的先验分布分别为均匀分布

πα=U(0,1),和πλ=U(0,c).

(5)

为了保证Bayes估计的稳健性，此时c是一个常数且不宜过大.

定理2.1当式(1)在Linex损失函数和两层先验式(4)、式(5)下时，参数θ的多层Bayes估计为

证明由式(4)和式(5)知，θ的先验分布为

从而θ的后验分布为

进而得

所以在损失函数(2)下，θ的多层Bayes估计为

利用数值积分可得θ的多层Bayes估计δB(X).

3 数值模拟

当尺度参数σ=0.45，形状参数β=0.8，n=50时，使用Matlab生成Weibull分布的随机数据，由这些数据计算得到，当n=50时，T=29.064 0，b=3.根据定理1.2中得出的参数θ的Bayes估计δB(X)，计算结果如表1所示.

表1 Linex损失函数下的Bayes估计

由表1可以看出，在Linex损失函数下，参数θ的Bayes估计δB(X)横向极差不超过0.062 011,纵向极差不超过0.041 639.从统计决策中稳健性角度看，δB(X)是很稳健的.由偏差△δ=|δB-θ0|(其中δB为参数θ的估计量，θ0为参数θ的真值，θ0≈2.222 2)得到偏差区间为[0.525 1,0.628 7].偏差区间较小，所以参数θ的Bayes估计δB(X)的精确度比较高.与文献[11]相比较可知，Weibull分布在Linex损失函数下与复合Linex损失函数下得到的参数的Bayes估计极差都较小，即稳健性均较好；但该分布在Linex损失函数下估计量更接近真值，偏差更小，即精确度更高.