一类Ornstein-Uhlenbeck算子的狄利克雷问题*
2022-05-10王愉靖
王愉靖
(广西师范大学 数学与统计学院,广西 桂林 541006)
1 引言
偏微分方程自十八世纪发展至今,其内容在广度和深度上不断拓展,应用范围日益广泛.偏微分方程可以描述许多实际问题,在医学、生物学、物理学、化学、环保、农业甚至是经济等领域发挥着非常重要的作用. 偏微分方程中有三类典型的方程,椭圆型偏微分方程、抛物型偏微分方程以及双曲型偏微分方程,其中的椭圆型偏微分方程的弱解的存在性问题一直是研究的热门话题. 证明椭圆型偏微分方程的弱解的存在性的方法有很多,例如变分法、拓扑度法、Galerkin近似法、单调算子法等等.其中单调算子法是证明非线性椭圆型偏微分方程弱解的存在性的一种比较常用的方法,该方法主要运用于具有单调性结构的方程.单调算子理论起初由Browder F. E.[1]提出,随后Leray J.和Lions J. L.在[1]的基础上得到一个新的算子——Leray-Lious算子[2].
令Ω为N的有界开集,N≥2,考虑一类非线性椭圆方程
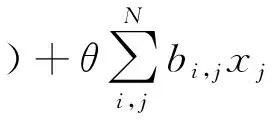
(1)
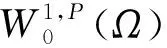
(1) 对于几乎所有的x∈Ω,a(x, )在N上是连续的;
(2) 对于∀ξ∈N,a(,ξ)在Ω上是可测的.
函数a(x,ξ)满足Leray-Lious算子的假设,即满足,对几乎每个x∈Ω,∀ξ,η∈N,ξ≠η有
上述假设也称为单调性假设.
1965年Leray J.和Lions J. L.在文献[2]中得到了方程
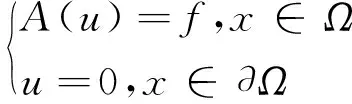
(2)
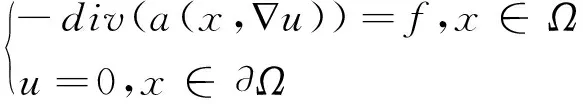
(3)
的解的问题被多个作者在不同的空间在f的多种形式下讨论过[2-5].
1989年Boccardo[3]研究了具有低阶项的狄利克雷问题
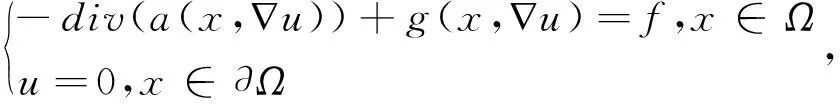
(4)
其中f∈L1(Ω),g是非线性的低阶项, 且满足g(x,∇u)·u≥0,的弱解的存在性.该文主要是通过求解近似问题来完成证明的.它首先构造近似问题,然后得到近似解的估计,最后由极限过程得到结果.此外文章[7,8,9]也讨论了此类方程的解的问题.
本文在前人工作的基础上研究一类Ornstein-Uhlenbeck[10,11]算子的狄利克雷问题
(5)
其中f∈Lp(Ω)是给定的已知函数.
本章内容主要分为三步:首先利用Galerkin近似法构造近似解,其次根据Minty法和条件[2]得到弱解的存在性和唯一性,最后运用截断函数证明弱解的连续性.
2 预备知识
本节主要介绍用到的定义、性质以及定理.在本文Ω为N的有界开区域,对于x=(x1,x2,…,xN)∈Ω,记函数u=u(x)和f=f(x)均为Ω到的实值函数;记∇u=(∇1u,∇2u,…,∇Nu).
定义2.1[13]设u为Ω⊂N上的可测函数,定义u的Lp范数为
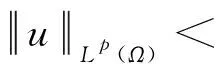

un→u,在Lp(Ω)中.

则称un在Lp(Ω)中弱收敛于u,记作
un⇀u,在Lp(Ω)中.
定义2.4[13]设m为正整数,1≤p≤∞,定义u的范数为
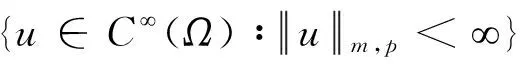
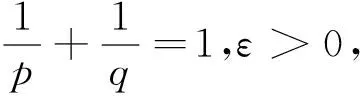
ab≤εap+c(ε)bq,
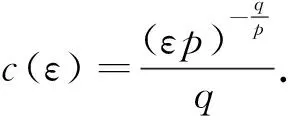
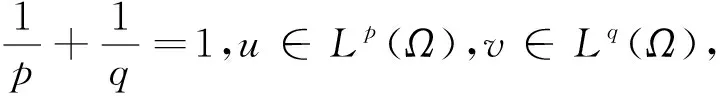
定理2.8[15]设Ω为N的有界开集,假设∞,则
其中C仅与p、N、Ω有关.
引理2.9[15]假设函数V∶N→N,满足V(x)x≥0,|x|=r,对于一些r>0,则存在一个点x∈(0,r),使得V(x)=0.
引理2.10假设e1,e2,e3,…,eN∈,则有
此引理的不等式就是熟知的均值不等式.
3 弱解的存在性与唯一性

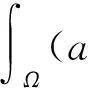
则称u为方程(5)的弱解.
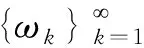
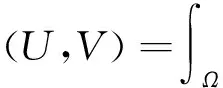
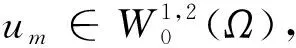
(6)

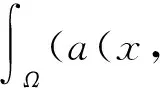
(7)
命题3.3[15]对于每个整数m=1,2,…,存在等式(6)的函数um满足等式(7).
证明引入光滑函数V∶m→m,V=(v1,v2,…,vm),

(8)
其中每个点d=(d1,d2,…,dm).现在
计算逼近均方根误差(Root Mean Square Error or Approximation, RMSEA)[12]和卡方(卡方/自由度,Chi-Square/Degree of Freedom)[13]用于验证所建立的结构化模型的适用性。RMSEA≤0.05则表明模型适用,而当其值近似为0.08或更少仍然意味着合理的逼近误差。相应的CMIN/DF值<3表示模型适用。

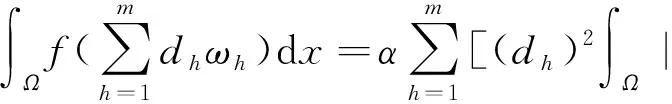

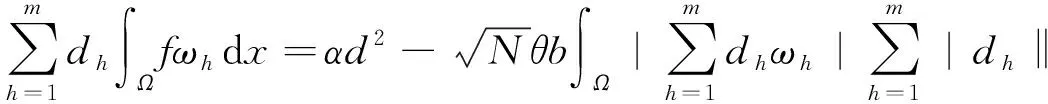

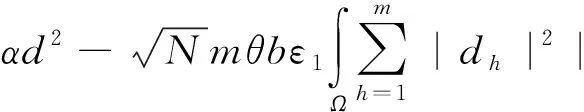
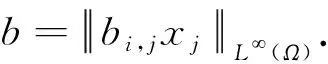
V(d)d≥0,|d|=r.
运用引理2.9可得,存在一些d∈m使得V(d)=0成立.换言之,等式(8)意味着由等式(6)定义的um满足等式(7).

命题3.4 存在一个常数c2,使得
成立.其中c2仅与函数a,Ω,bi,j有关.
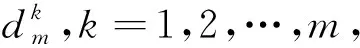
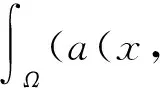
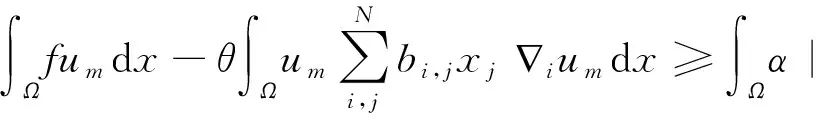
经运算得
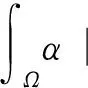
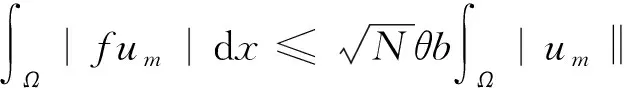
合并同类项有
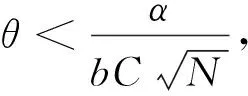
我们将定理3.5分成两个命题来证明.

证明分以下四个步骤证明这个命题.
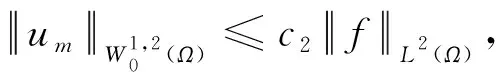
(9)
接下来要证明u满足等式
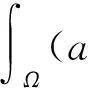
第二步.运用[1]有|a(x,∇um)|≤β|∇um|,所以在L2(Ω;N)中有界,从而可假设
a(x,∇um)⇀ζ,在L2(Ω;N)中,
(10)
对于一些ζ∈L2(Ω;N)成立.
利用等式(7)
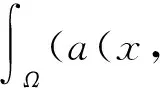
有m→∞时,

因此有

(11)
第三步.由[2]有
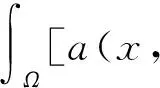
变形后得到
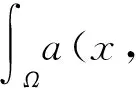
(12)
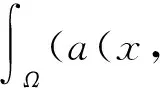
将式(12)代入上式有
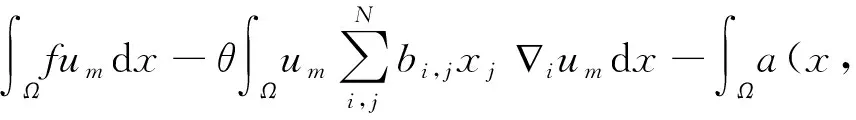
其中m=1,2,….
运用式(9)、(10),令m=mh→∞可得
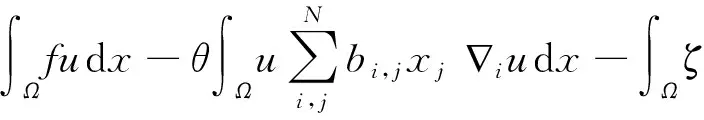
(13)
令等式(11)中的v=u,有

(14)
将式(14)代入式(13)得到

即

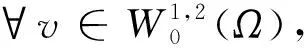
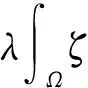
约去λ,有

令λ→0,得到

令v=-v,有

因此
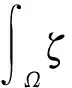
(15)
将式(11)代入式(15),有
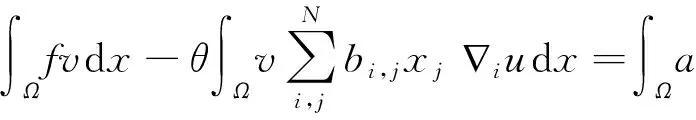
即
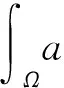
成立.
命题3.7方程(5)的弱解是唯一的.
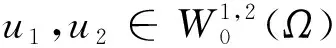
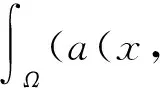
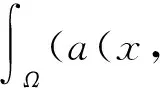
两式相减有
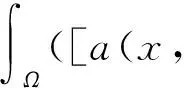
令v=u1-u2,可得
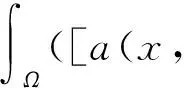
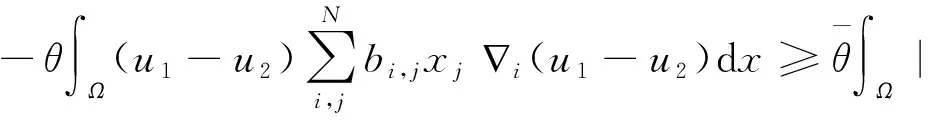
通过运算得
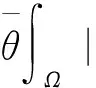
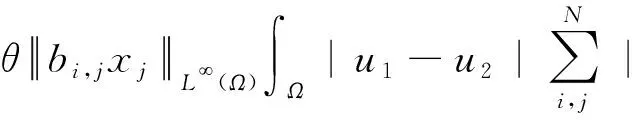


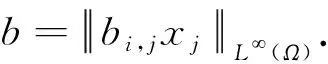
合并同类项得
即

由此得出u1-u2=0.因此定理3.5成立.
4 解的连续性
在第3节我们得到了方程(5)的弱解的存在唯一性,下面讨论弱解的连续性.考虑如下非线性边值问题:
(16)
和
(17)

定义4.1
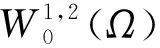
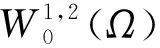
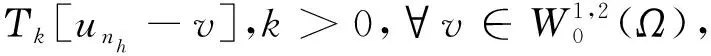
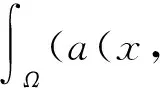
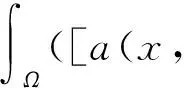
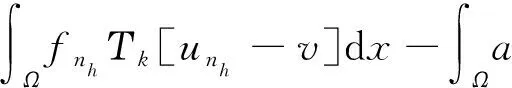
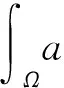
由于Τk[un-v]在L2(Ω)中强收敛,故当nh→∞时有
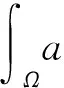
当k→∞时有(由Τk(s)的定义)
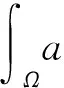
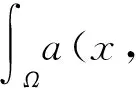
约去t,得到
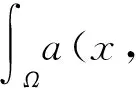
令t→0有
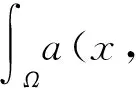
令ω=-ω,得到
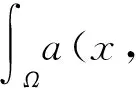
因此可得出
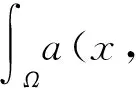
由于u∞为方程(17)的弱解,即
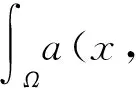
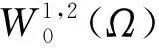
5 结束语
偏微分方程是数学的一个重要组成部分,是自然科学与工程技术等领域衔接的一个不可或缺的桥梁,许多领域的问题都可以用偏微分方程来描述.本文用Galerkin近似法、Minty法以及单调性去解决非线性椭圆型偏微分方程的存在性问题.与本文有关的还有一些地方值得研究,例如p>2或1
