S 盒可分特征的线性不等式刻画研究*
2022-05-10胡建勇张文政董新锋苗旭东
胡建勇,张文政,董新锋,周 宇,苗旭东
(1.中国电子科技集团公司第三十研究所,四川 成都 610041;2.保密通信重点实验室,四川 成都 610041)
0 引言
近年来,随着可分性质[1]的提出,基于可分性质的积分分析[1-8]被相继提出,并逐步走向自动化,日趋成熟。S 盒作为常用的非线性密码部件,其可分性质的传播严重影响积分路径的长度,因此S 盒可分特征的刻画成为自动化积分分析的关键。根据细粒度的不同,S 盒可分特征的刻画可分为比特级刻画和非比特级刻画。
2015 年,Todo 等人给出了S 盒可分性质的非比特级传播规则[1],在代数次数已知的情况下,可以计算出所有的可分特征,但并没有给出非比特级刻画。
2016 年,向泽军等人给出了S 盒比特级可分特征的计算方法[4],借助Sage Math 工具[9],使用线性不等式,成功实现比特级刻画。但比特级刻画存在两个问题:一是比特级刻画与S 盒的代数表达式有关,不具备一般性,无法支持动态S 盒[10-13]的刻画;二是对于大状态盒,其比特级刻画使用的线性不等式数量庞大,这会严重影响自动化分析模型的求解效率,甚至无法有效求解。
2017 年,孙玲等人使用布尔逻辑方程,给出了S 盒可分特征的非比特级刻画[5],但这种刻画同样不具备一般性,不支持动态S 盒的刻画,同时也不支持混合整数线性规划问题(Mixed Integer Linear Programming,MILP)的求解器。
因此,为解决S 盒非比特级可分特征的刻画问题,使其具有通用性,同时支持MILP 求解器,本文研究了可分特征的线性不等式刻画,给出3 种刻画方法及其一般刻画形式,其中,凸包的H 表示方法使用的线性不等式数量最少,并且不使用临时变量,但无法实现等价刻画;大M 方法在增加一个二进制临时变量的情况下,能够实现等价刻画,但使用的线性不等式数量最多;维数扩充法同样增加一个二进制临时变量,实现等价刻画,并且使用的线性不等式数量与凸包的H 表示方法相当,刻画效果达到最优。
1 相关知识

设两个m维向量a=(a0,a1,…,am-1)和b=(b0,b1,…,bm-1),若对于i=0,1,…,m-1,都有ai≥bi,则称向量a大于等于向量b,记为a≥b。
定义1(可分性质):设X是一个多重集,其元素都取值于,K是由m维向量构成的集合,对于任意的正整数向量k∈K,k的第i+1 个分量ki取值范围为0 ≤ki≤ni-1,如果对所有x∈X,满足:

那么就称多重集X满足可分性质特别地,当n0=n1=…=nm-1=1 时,多重集X满足比特级可分性质。
对于n比特S 盒,设其输入多重集满足的可分性质为Dkn,对应的输出多重集满足的可分性质记为,于是(k,k´)称为S 盒的可分特征。假设S 盒的代数次数为d,根据S 盒可分性质的非比特级传播规则,则可分特征(k,k´)满足:
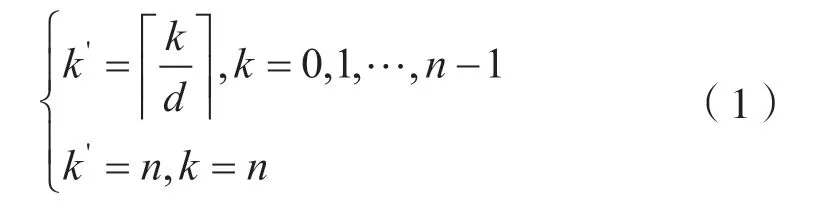
因此,在已知S 盒的状态大小n和代数次数d的情况下,可以根据式(1)计算出所有的可分特征,共计n+1 条。对于任意的一条可分特征(k,k´),它都可以看作二维平面上的一个点。于是,这n+1 条可分特征可以看作二维平面上的一个点集,记为Vn,d,从而S 盒可分特征的刻画实际上是对集合Vn,d的刻画。
对于集合V,其线性不等式刻画是指寻找一些线性不等式Λ,使得任意的x∈V都是Λ 的可行解。特别地,当Λ 的所有可行解恰好构成这个集合V时,则称Λ 是V的等价刻画,否则称为非等价刻画。Λ的求解效率取决于线性不等式的数量和变量的个数。因此,在自动化分析中,优先使用等价刻画,并且尽量要求线性不等式的数量和变量的个数尽量小。
2 凸包的H 表示方法
对于集合V,所有包含V的凸集的交集称为V的凸包,其本质是指一个最小凸多面体,满足V中的元素要么在凸多面体上,要么在其内部。特别地,当V是由二维平面上的一些点构成的集合时,它的凸包就是将最外层的点连接起来构成的凸多边形。
使用凸包的H 表示方法刻画集合V,实际上是对V的凸包进行等价刻画,这个凸包由一些平面或者直线划分而成,只要计算每一个平面或者每一条边并根据它们与V的相对位置,便能够得到线性不等式刻画。如果凸包中存在一个元素不属于V,那么得到的线性不等式刻画是V的非等价刻画。
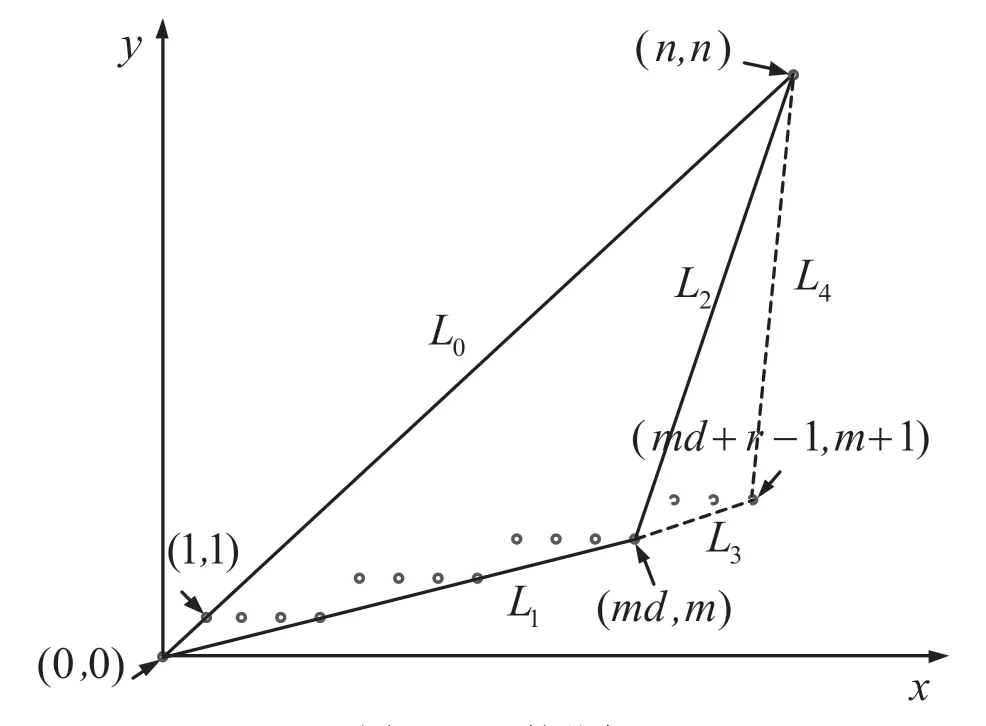
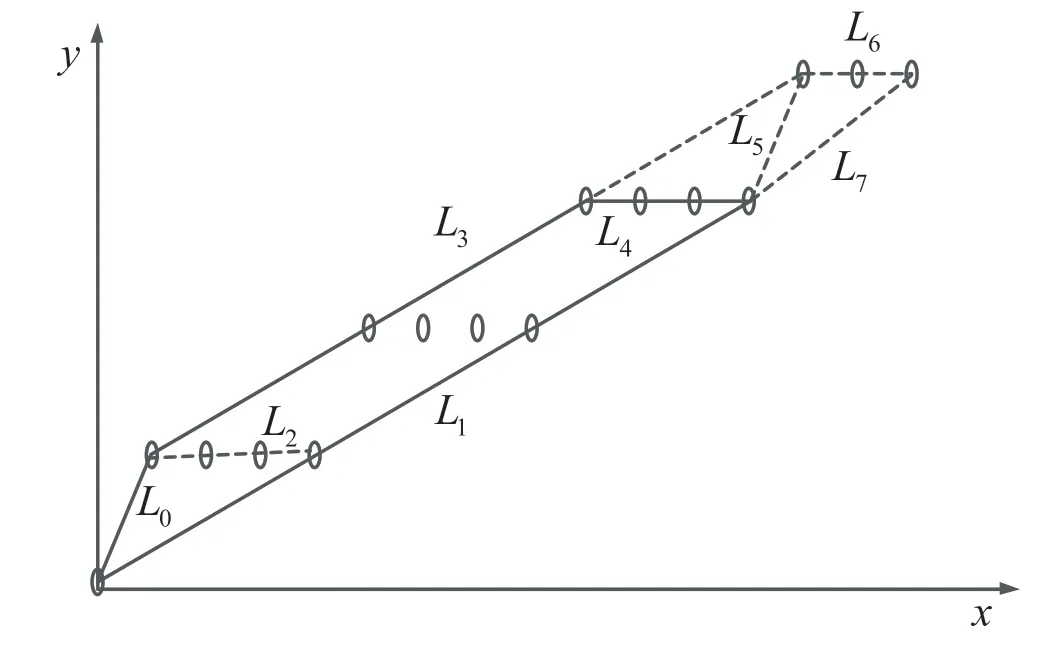
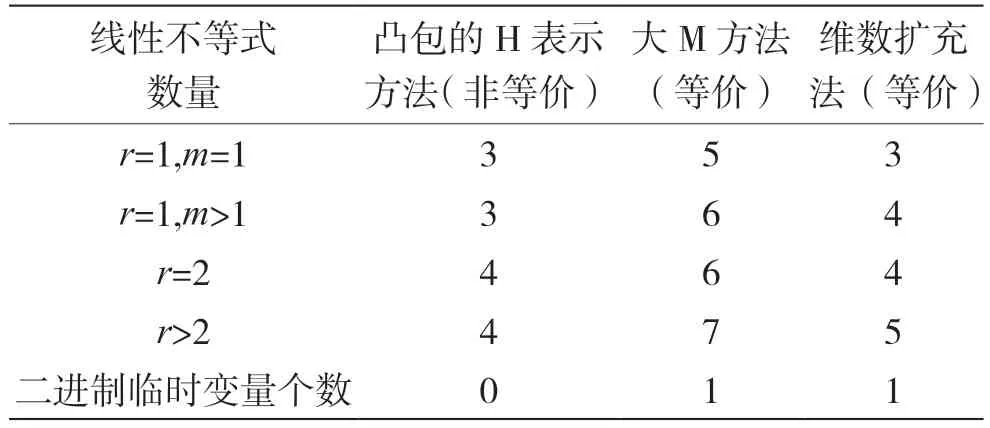
对 于n比特S盒,不妨设n=md+r,其中0 建立二维空间坐标系,连接最外层的整数点,如图1 所示。 图1 Vn,d 的凸包 (1)当r=1 时,最外层的整数点(0,0),(1,1),(n,n)和(md,m)形成三角形,由直线L0:y=x,和L2:y=(n-m)x-(n-m-1)划分而成,得到一般刻画形式: (2)当r>1 时,最外层的整数点(0,0),(1,1),(n,n),(md+r-1,m+1)和(md,m),形成凸四边形,由直线和L4:y=(n-m-1)x-(n-m-2)n划分而成,得到一般刻画形式: 于是,通过式(2)或式(3)实现了Vn,d的刻画。 由于Vn,d的凸包中包含了不属于Vn,d的整数点,因此式(2)或式(3)是Vn,d的非等价刻画。 大M 方法是在线性规划中解决条件约束的形式化问题而被提出的[14]。设条件约束中的A1x≤b1和A2x≤b2至少有一个成立。大M 方法通过引入二进制临时变量y和设置大数M实现条件约束: 如式(4)所示,当临时变量y=0 时,A2x≤b2+M恒成立,约束条件为A1x≤b1;当临时变量y=1 时,A1x≤b1+M恒成立,约束条件为A2x≤b2。 定义2(离散凸集):设集合V是一个由整数点构成的集合,如果集合V的凸包中包含的所有整数点都恰好属于集合V,则称集合V是一个离散凸集,否则称集合V不是一个离散凸集。 显然,根据离散凸集的定义,使用凸包的H 表示方法刻画离散凸集必然属于等价刻画。 性质1:Vn,d不是一个离散凸集。 证 明:由 于(0,0) ∈Vn,d,(n,n) ∈Vn,d,这 两点的连线必然包含于Vn,d的凸包,因此凸包中包含整数点(k,k),k=0,1,…,n。由于S盒的代数次数d>1,根据可分特征的非比特级传播规则,(2,2),(3,3),…,(n-1,n-1)都不是S 盒的可分特征,不满足离散凸集的定义,因此Vn,d不是离散凸集。 证明:不妨设n=md+r,其中0 建立二维空间坐标系,连接最外层的整数点,如图2 所示。 图2 的凸包 当r=1,m=1 时,最外层整数点连接的图形是一个三角形,由直线和L2:y=1划分而成;当r=1,m>1 时,最外层整数点连接的图形是一个梯形,由直线和L4:y=m划分而成;当r=2时,最外层整数点连接的图形是一个平行四边形,由直线和L:y=x-m(d-1)划分而成;当r>2 时,最外层整数点连接的图形是一个凸五边形,由直线L0:y=x,,L6:y=m+1以及划分而成。这些凸多边形构成的凸包,并且凸包中包含的所有整数点恰好都属于集合。因此,是一个离散凸集。 注意到单个整数点构成的集合一定是一个离散凸集。于是,Vn,d可以划分为和{(n,n)}两个离散凸集。使用凸包的H 表示方法计算和{(n,n)}的等价刻画,它们便形成了条件约束,从而利用大M 方法可以得到Vn,d的一般刻画形式。 (1)当r=1,m=1 时, (2)当r=1,m>1 时, (3)当r=2 时, (4)当r>2 时, 式中:b∈F2;M是一个较大的正整数。 于是,式(5)、式(6)、式(7)和式(8)等价刻画了Vn,d。 维数扩充法的主要思想是对集合Vn,d的维数进行扩充,使得扩充后的集合成为离散凸集,然后结合凸包的H 表示方法,实现Vn,d的等价刻画。 性质3:设V={(b,c)|b,c∈Z}是一个离散凸集,对于任意的整数a,令E(a,V)={(a,b,c)|b,c∈V},则E(a,V)同样是一个离散凸集。 证明:建立三维空间的坐标系(t,x,y),对于二维空间上的任意整数点(b,c)∈V,都可以将它看作三维空间平面t=0 上的整数点(0,b,c),整数点(a,b,c)是(0,b,c)沿着t轴方向的平移点。因此,E(a,V)中的全部整数点都是V中对应整数点沿着t轴方向的平移点,并且平移的距离都为a。在这种平移下,点的相对位置保持不变。V是一个离散凸集,其凸包内所有整数点恰好都属于集合V。这个凸包经过相同的平移,构成E(a,V)的凸包,它包含的整数点恰好也都属于集合E(a,V)。因此,E(a,V)是一个离散凸集。 对于任意的整数a和b,令E(b,{(n,n)}),于是满足性质4。 性质4:当|a-b|=1 时,是一个离散凸集。 证明:建立三维空间的坐标系(t,x,y),于是E(a,) 中的点全部位于平面t=a上。E(b,{(n,n)})={(b,n,n)},点(b,n,n)位于平面t=b上,可以看作平面t=a上的点(a,n,n)沿着t轴方向正向或者反向平移的点,由于|a-b|=1,平移的距离等于1,在平面t=a和平面t=b之间不含整数点。由于是离散凸集,根据性质3,E(a,)同样是离散凸集,在平面t=a上,存在一个凸包,使得凸包中所有的整数点恰好都属于集合,这个凸包是一个凸多边形,如图3 所示。将整点与凸多边形上的每一个顶点相连,从而形成棱锥,它是的凸包,并且其包含的整数点恰好都属于。因此,是一个离散凸集。 图3 Vspn,d 的凸包 于是,Vn,d的等价刻画实际上就是的等价刻画。由于中引入了临时变量t,取值为a或者b。为了便于自动化分析模型的求解,限定t为二进制变量,不妨令a=1,b=0。 (1)当r=1,m=1 时,的凸包是一个三棱锥,由平面t=0,t=1,x-y=0,(n-1)t+y-n=0 和平面n(n-2)-n(n-2)t+x-(n-1)y=0 划分而成,等价刻画的一般形式为: (2)当r=1,m>1 时,的凸包是一个四棱锥,由平面t=0,t=1,x-y=0,(n-m)t+y-n=0,-n(d-1)t+xdy+n(d-1)=0 和平面(n-1)(d-1)t-x+dy-n(d-1)=0 划分而成,等价刻画的一般形式如式(10)所示。 (3)当r=2 时,的凸包是一个四棱锥,由平面t=0,t=1,x-y=0,-n(d-1)t+x-dy+n(d-1)=0,(n-1)(d-1)t-x+dy-n(d-1)=0 和平面m(d-1)t+x-y=0 划分而成,等价刻画的一般形式为: (4)当r>2 时,的凸包是一个五棱锥,由平 面t=0,t=1,x-y=0,(n-m-1)t+y-n=0,-n(d-1)t+x-dy+n(d-1)=0,(n-1)(d-1)t-x+dy-n(d-1)=0 和 平面((n-m)(1-r)+r)t+x-(r-1)y+n(r-2)=0 划分而成,等价刻画的一般形式如式(12)所示。 于是,式(9)、式(10)、式(11)、式(12)同样等价刻画了Vn,d。 针对集合,在不同和的取值下,使用凸包的H表示方法、大M 方法和维数扩充法得到线性不等式刻画。如表1 所示,不同刻画方法在刻画类型、线性不等式数量和二进制临时变量个数方面各不相同。 表1 不同刻画方法的刻画效果 凸包的H 表示方法不会引入临时变量,得到的线性不等式刻画属于非等价刻画,而大M 方法和维数扩充法需要引入1 个二进制临时变量,得到的线性不等式刻画属于等价刻画。使用凸包的H 表示方法,对应的线性不等式数量最少;使用大M 方法,对应的线性不等式数量最多;而使用维数扩充法,对应的线性不等式数量与凸包的H 表示方法相当。因此,与凸包的H 表示方法和大M 方法相比,维数扩充法的刻画效果最优,对应的线性不等式是最优刻画。 为了验证一般形式的正确性,针对常用的4 比特S 盒和8 比特S 盒进行了实验验证,验证结果如表2 所示,不同刻画方法对应的一般形式均能正确地刻画S 盒非比特级可分特征,其中凸包的H 表示方法对应的一般形式是非等价刻画,大M 方法和维数扩充法对应的一般形式为等价刻画。 本文旨在解决S 盒非比特级可分特征的线性不等式刻画问题,给出了凸包的H 表示方法、大M方法和维数扩充法3种刻画方法及其一般刻画形式。其中,大M 方法和维数扩充法首次实现了S 盒非比特级可分特征的等价刻画,并且维数扩充法通过引入一个二进制临时变量,在实现等价刻画的同时,对应的线性不等式数量最少,是一种最优刻画方法,对应的一般形式可直接应用于分组密码的自动化积分分析中。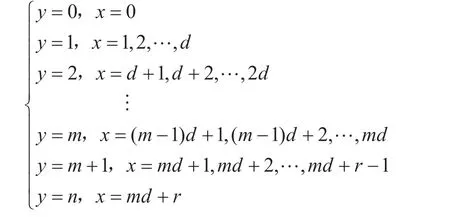
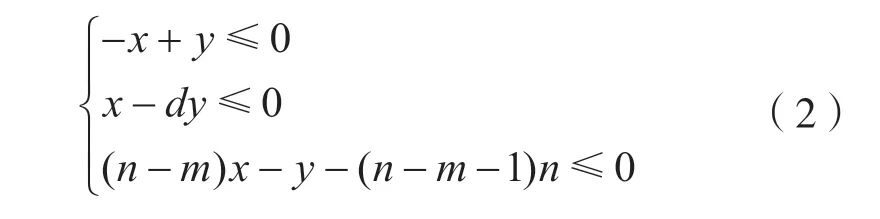
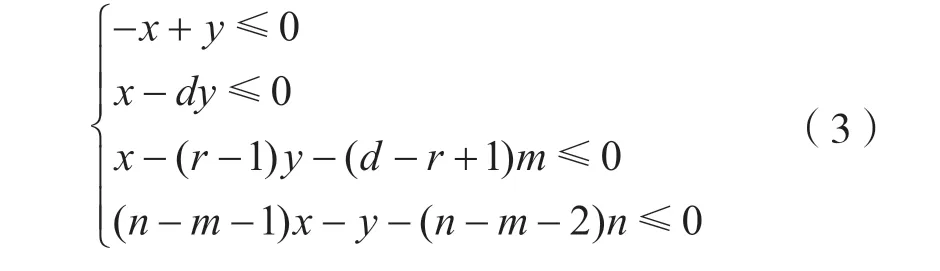
3 大M 方法
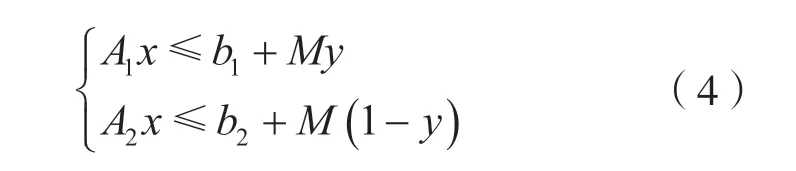


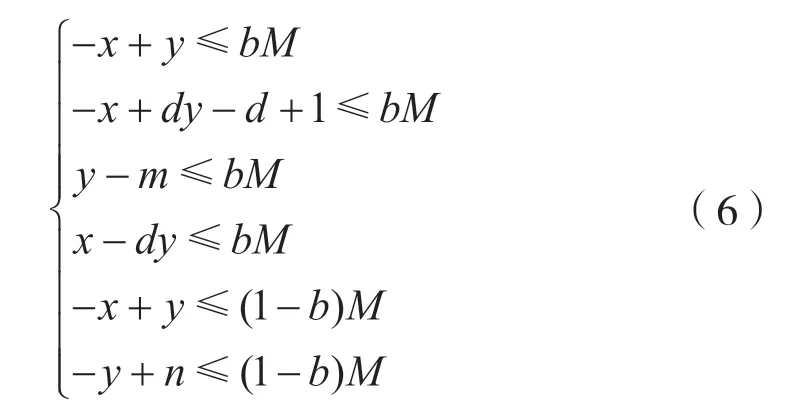
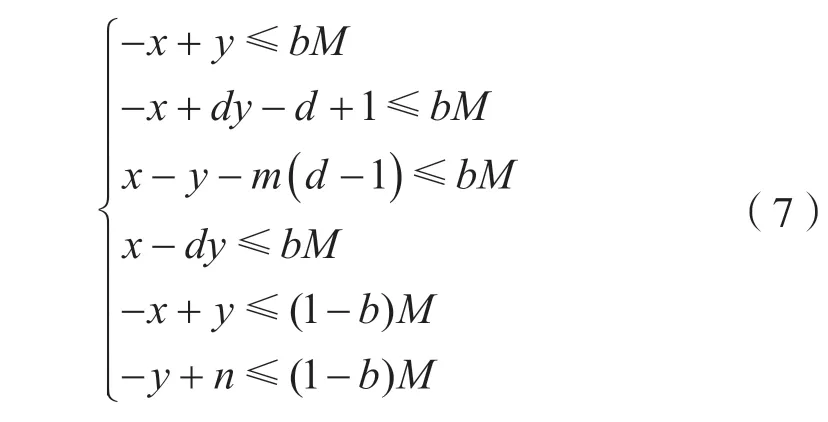
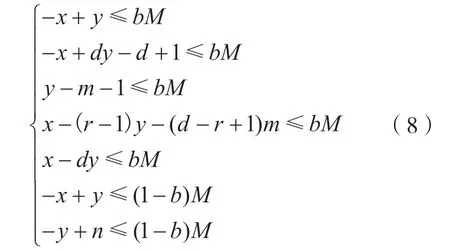
4 维数扩充法
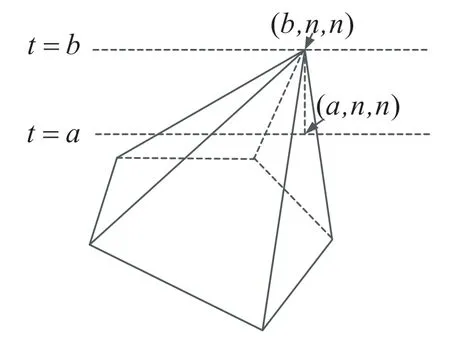
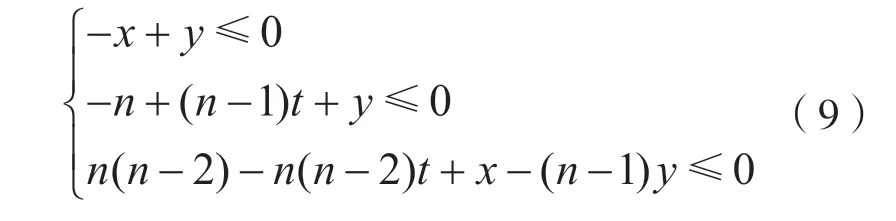

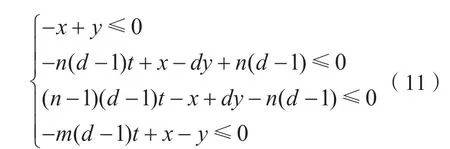
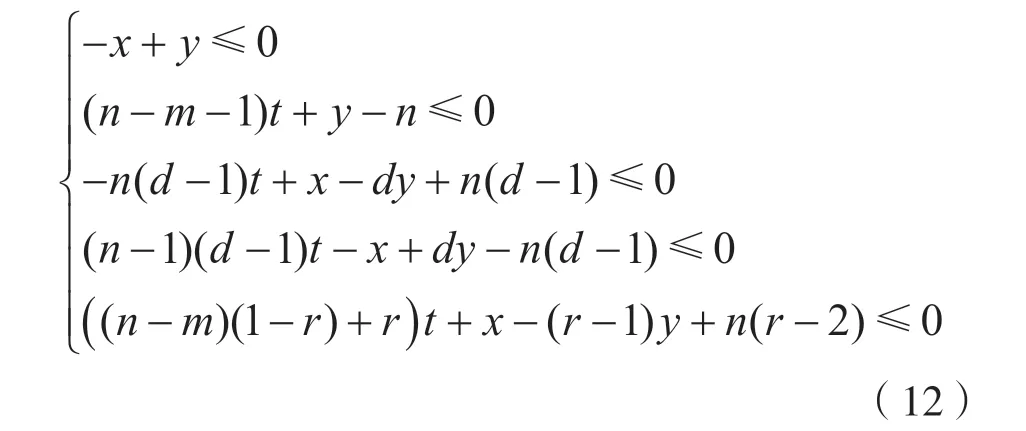
5 刻画效果对比
6 结语
