基于应变的高钢级管道环焊缝适用性评价*

杨辉 王富祥 钟婷 玄文博 雷铮强

(国家管网集团北方管道公司管道科技研究中心)

0 引 言

西气东输一线管道的建设拉开了我国长输油气管道全面应用高钢级管道的序幕，目前我国已投产的在役X80管道已超过1.3万km。国内管道大建设的同时也暴露了诸多问题，其中高钢级管道环焊缝的脆弱性尤其突出[1-8]。现行的管道设计标准大多遵循传统的基于应力的设计准则，但管材出现屈服和应变强化时，基于应力的设计准则便不再适用[9-11]。预测在大变形条件下含缺陷管道的应变能力，或预测在一定应变要求下管道的缺陷容限水平，是大范围屈服条件下管道基于应变断裂评估的主要动因[12-13]。基于应变的评价需要解决两个关键问题，分别为驱动力的应变表征和失效准则的确定[14]。

杨辉等[15]基于CSA Z662—2011标准推荐的拉应变极限公式，采用有限元法分析了不同因素下含裂纹管道的极限承载力，但并未给出裂纹驱动力的应变表征。韩克江等[16]评估了管道大范围屈服断裂评估现状，从驱动力方程和裂纹尖端张开位移(CTOD)准则两方面介绍了基于应变的断裂评估方法，偏于理论研究。基于此，笔者通过对含环焊缝根部裂纹的高钢级管道进行有限元分析，得到基于应变的裂纹扩展驱动力，明确了缺陷尺寸、强度匹配及压力等因素对环焊缝应变能力的影响；对比分析了两种管道环焊缝断裂失效准则并明确了其适用性，以期为高钢级管道环焊缝应变能力评估提供技术参考。

1 环焊缝根部裂纹有限元模型

1.1 几何模型

为方便建模和计算，对内表面裂纹进行以下简化：假设裂纹深度均匀，大小为a，裂纹环向长度为2c，在裂纹两端采用半径r=a的圆弧过渡，这种“独木舟”形式的裂纹可以很好地模拟实际环形焊缝裂纹的形状。图1为管道环焊缝根部裂纹几何模型。

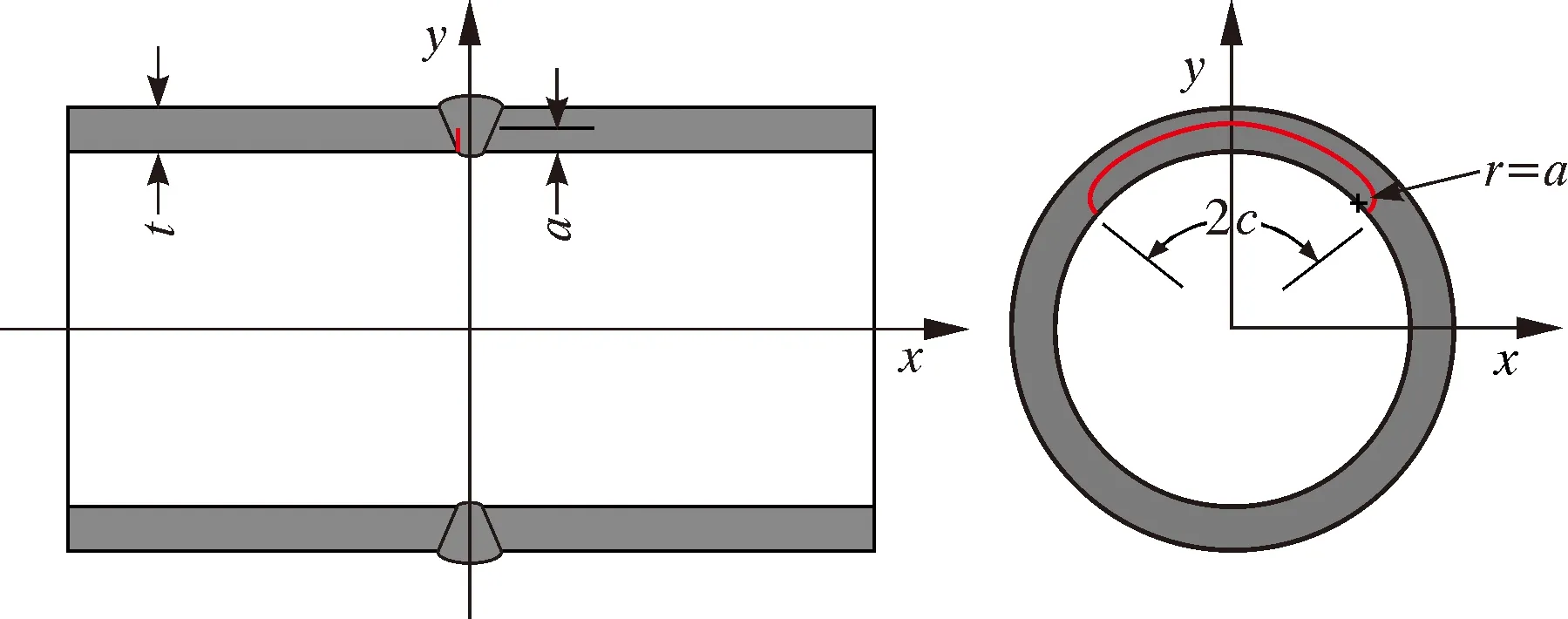
图1 管道环焊缝根部裂纹几何模型Fig.1 Geometric model of pipeline with crack at the root of girth weld

1.2 有限元建模

运用ABAQUS软件建立了含环焊缝根部裂纹的X80管道有限元模型，如图2所示。图2为对称模型。直径D和壁厚t分别为1 219和18.4 mm，考虑两种不同的裂纹深度，分别为a/t=0.1和0.3，两种不同的裂纹长度均用弧度表示，长分别为π/36和π/18。裂纹尖端区域网格要求足够精细，同时采用过渡网格控制网格总量，保证精度的同时提高计算效率。除缺陷外，还考虑强度匹配、内压、错边及变壁厚等因素的影响。

图2 管道环焊缝根部裂纹有限元模型Fig.2 Finite element model of pipeline with crack at the root of girth weld

1.3 材料本构

对于母材和焊缝，采用Ramberg-Osgood模型描述的应力应变曲线。该模型为业内广泛认可的材料非线性本构模型之一[17-18]，被众多标准引用，适用于管线钢。应力应变计算式为：

(1)

(2)

(3)

式中：ε为应变，无量纲；σ为应力，MPa；E为弹性模量，取210 GPa；σY为屈服强度，MPa；σT为抗拉强度，MPa；n为硬化指数，无量纲；α为屈服偏移量，无量纲。

目前，国内外相关管道设计与评价标准对强度匹配的定义尚不统一，如BS 7910《金属结构裂纹验收评定方法指南》、DNVGL-ST-F101《海底管道系统》建议采用屈服强度作为强度匹配参数。CSAZ662《油气管道系统》指出，因制管过程使得管道轴向屈服强度与环向屈服强度存在较大差异，但对管材抗拉强度影响较小，故应以抗拉强度作为强度匹配参数来确定焊缝区材料。此外，ExxonMobil和CRES等研究机构也提出采用抗拉强度作为匹配参数[19-20]。

由于工程中对于焊接接头抗拉强度的评定相对容易，所以文中选取抗拉强度作为强度匹配系数，考虑高匹配10%、等匹配、低匹配10%及低匹配20%等4种强度匹配形式。

2 管道环焊缝应变能力影响因素分析

2.1 基于应变的裂纹扩展驱动力

明确基于应变的裂纹扩展驱动力是基于应变断裂评估的重要一环，而管道缺陷尺寸(缺陷长度和深度)、缺陷位置、材料性能(强度匹配)、焊缝几何特征及其载荷方式等因素对管道裂纹驱动力均存在影响，是评价管道应变能力的重要依据。在基于应变设计中，应变一般采用管道远端应变来表征，远端应变是指在管道模型远离裂纹处的均匀轴向应变[21]。为节省计算资源，有限元数值分析中仅仅取一定长度的管道，因此需要确定合适位置的应变代表管道的远端应变，文中取远端整个壁厚应变的平均值ε为管道的远端应变，从有限元结果中提取裂纹尖端张开位移(DCTO)作为裂纹扩展驱动力参量。

2.2 缺陷尺寸对裂纹驱动力的影响

缺陷尺寸不仅影响裂纹扩展阻力，而且影响裂纹扩展的驱动力。本文研究了4组不同缺陷尺寸下的基于应变的裂纹驱动力影响，分别是裂纹深厚比a/t=0.1和0.3、裂纹长度分别为π/36和π/18时，结果如图3所示。在裂纹深厚比a/t=0.1时，裂纹长度对基于应变裂纹驱动力的影响较小，因为此时管道失效不是由裂纹失稳断裂所控制，而是由韧带塑性失稳控制；在裂纹深厚比a/t=0.3时，裂纹长度对基于应变裂纹驱动力的影响较为明显。同时在裂纹长度为π/18和π/36时，裂纹深度对基于应变裂纹驱动力的影响都较为明显。由此可见，基于应变裂纹驱动力对于缺陷深度尺寸要更为敏感。

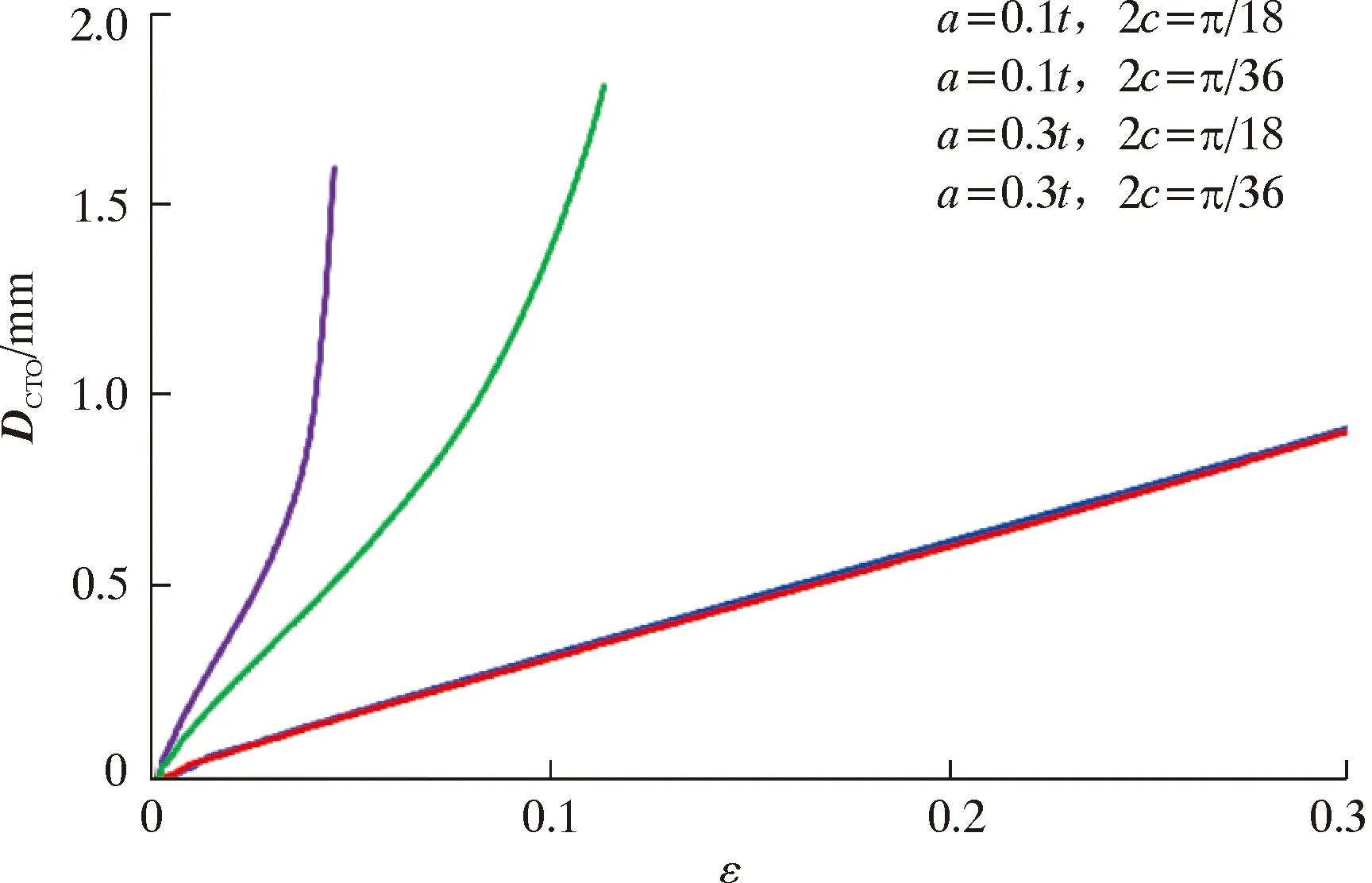
图3 不同缺陷尺寸下的裂纹驱动力Fig.3 Crack driving force under different defect sizes

2.3 强度匹配对裂纹驱动力的影响

理论上，通常要求焊缝区材料相对母材采用高强或等强匹配，但实际工程中管道强度性能数据方差较大，导致母材实际的屈服强度往往远大于规定的最小屈服强度，造成高强钢管道环焊缝出现实际低匹配的情况[22-23]。本文研究了4种不同强度匹配形式(低匹配20%、低匹配10%、等匹配和高匹配10%)对驱动力曲线的影响，结果如图4所示。由图4可以看出，高匹配焊接对环焊缝的承载能力有一定的增强作用，相较于低匹配，高匹配情况下的驱动力曲线逐渐向右侧倾斜(斜率减小)，即以相同的DCTO表征断裂韧度时，高匹配焊接的环焊缝具备更强的应变能力，其承载能力也相应增强。同时，随着匹配系数的增加，曲线间距减小，承载能力的增幅在逐渐减小，说明高匹配焊缝再单纯提高强度并不能有效提升其承载能力。

图4 不同匹配情况下的裂纹驱动力Fig.4 Crack driving force under different matching conditions

2.4 内压对裂纹驱动力的影响

在基于应力的工程临界评估中，仅仅垂直于裂纹平面的应力才被用于裂纹驱动力的评估中[24-25]。对于含环向环焊缝裂纹缺陷的管道，在内压作用下，管道裂纹受到双轴载荷的作用，由内压产生的环向应力改变了裂纹尖端应力应变场，如仅仅考虑轴向应力而忽略内压产生的环向应力，其评估结果可能偏保守。本文分别模拟得到了无内压、内压5和10 MPa下的裂纹驱动力曲线，如图5所示。

由图5可以看出，内压的增加造成驱动力曲线向左倾斜(斜率增大)，即DCTO相同时，环焊缝随着内压的增加其应变能力下降，进而导致承载能力下降。

图5 不同内压下的裂纹驱动力Fig.5 Crack driving force under different inner pressures

2.5 错边对裂纹驱动力的影响

高钢级管道在焊接和装配过程中易出现错边现象，错边的存在使得管道结构连续性遭到破坏，会导致焊缝位置应力集中，同时产生附加弯曲应力，大大降低管道强度，进而影响管道安全运行。本文分别模拟了无错边、错边1.5和错边3.0 mm下的裂纹驱动力曲线，结果如图6所示。

图6 不同错边情况下的裂纹驱动力Fig.6 Crack driving force under different staggered edges

由图6可知，错边量的增大也造成驱动力曲线向左倾斜(斜率增大)，即错边造成环焊缝应力下降，且下降幅度明显。在管道的制造过程中一旦出现焊缝错边量偏差大的问题，极其不容易修复和纠偏，因此在管道焊接的过程中需要针对焊缝错边问题严格控制。

2.6 变壁厚对裂纹驱动力的影响

变壁厚钢管连接处焊接结构不连续，存在较大的应力集中。不等壁厚焊接时，根部焊接质量不易控制，易出现焊接缺陷。由于外形尺寸的不规则，无损检测时易出现根部缺陷漏检。通过对国内外环焊缝大量失效案例分析，也充分证实了这个问题。本文分别模拟了等壁厚(壁厚比=1.0)和变壁厚(壁厚比=1.2)两种情况下的裂纹驱动力曲线，结果如图7所示。由图7可知，变壁厚焊缝较等壁厚焊缝驱动力曲线向左倾斜(斜率增大)，即应变能力下降。

图7 不同壁厚比情况下的裂纹驱动力Fig.7 Crack driving force under different wall thickness ratios

3 基于应变的管道环焊缝评价方法

3.1 环焊缝断裂失效准则

采用DCTO作为参数描述裂纹扩展驱动力和裂纹扩展阻力。断裂力学理论认为[26]，当符合下列准则时，断裂将会发生：

δapp=δR

(4)

(5)

式中：δapp为外加裂纹驱动力，mm；δR为裂纹扩展阻力，mm；e为裂纹扩展量，mm。

由此，可以建立两种断裂失效准则：①材料断裂韧度准则，如式(4)所示，当外加裂纹驱动力等于裂纹扩展阻力时材料断裂失效，即通过标准试样测定的材料断裂韧度进行评价；②裂纹失稳扩展准则，如式(5)所示，当外加裂纹驱动力关于裂缝扩展量的导数等于裂缝扩展阻力的导数，即外加裂纹驱动力和阻力曲线相切于一点时发生失稳断裂，如图8所示。需要通过标准试样测定δ或阻力曲线进行评价，由于断裂韧度相关参量的尺寸敏感性，试验有效性难以保证[26-27]。

图8 断裂失稳模型Fig.8 Fracture instability model

图9 裂纹扩展驱动力曲线解析Fig.9 Analysis on crack propagation driving force curve

韩克江等[16]、帅健等[28]提出新的裂纹扩展失效准则，以不同裂纹长度的裂纹驱动力曲线为例，根据裂纹扩展情况，分为3个不同的区域(见图9)。区域1至区域2管道由整体弹性逐渐发展为塑性，裂纹韧带逐渐颈缩，区域2的驱动力曲线近似呈线性上升。随着载荷进一步增大，DCTO随着裂纹韧带坍塌而急剧增大，裂纹失稳扩展。可见，找到区域2和区域3的临界点对应的极限应变即为管道环焊缝断裂的临界应变。

3.2 环焊缝应变能力评价

基于上述两种断裂失效准则，分别评价含环焊缝裂纹(a=0.3t，2c=π/18和π/36)管道的应变能力，分别确定对应的临界应变，如图10所示。

图10 基于应变的环焊缝评价Fig.10 Strain-based evaluation on girth weld

从图10可知：随着裂纹长度的增大，按基于裂纹扩展失稳的失效准则，极限轴向拉伸应变由5.72%减小为2.53%，降幅为55.8%；而按基于材料断裂韧度的失效准则，应变能力由2.01%减小为1.22%，降幅为39.3%。图11为两种断裂失效准则下的极限应变。

图11 两种断裂失效准则下的极限应变Fig.11 Ultimate strains under two fracture failure criteria

基于裂纹失稳扩展失效准则评价的是管道极限应变能力，如果环向裂纹在母材扩展或焊缝区材料经过试验证实断裂韧度较好，且能够发生延性撕裂，可以采用该方法进行评价，以充分利用材料性能。但基于裂纹失稳扩展准则对环焊缝的断裂韧度要求很高，工程上不易达到。如果管道环焊缝的韧性不良，断裂韧度较低，则建议选择基于断裂韧度准则的评价方法，这在工程上是偏于安全并较为实际的做法。

4 结论及建议

通过有限元分析得到了基于应变的环焊缝裂纹扩展驱动力，分析了缺陷尺寸、强度匹配、内压、错边和变壁厚等因素对管道环焊缝应变能力的影响，得到如下结论：

(1)缺陷尺寸不仅影响裂纹扩展阻力，而且影响裂纹扩展的驱动力。裂纹深度较长度对基于应变裂纹驱动力的影响更为明显。

(2)高匹配焊接的环焊缝具备更强的应变能力，承载能力也相应增强。但随着匹配系数的增加，承载能力的增幅在逐渐减小，说明高匹配焊缝再单纯提高强度并不能有效提升承载能力。

(3)内压的增大导致环焊缝应变能力下降，在基于应力的工程临界评估中，如仅仅考虑轴向应力而忽略内压产生的环向应力，其评估结果是保守的。

(4)错边和变壁厚等根部不连续会产生明显的应力集中，削弱环焊缝的承载能力。结合断裂力学理论及裂纹扩展驱动力演化特征，对比分析了材料断裂韧度准则和裂纹失稳扩展准则两种管道环焊缝断裂失效准则，得出基于裂纹失稳扩展失效准则评价的是极限应变能力，对环焊缝的断裂韧度要求很高，工程上不易达到，因此建议选择基于断裂韧度准则的评价方法。