基于压电陶瓷换能器的埋地管道缺陷监测研究*

2022-05-10徐阳罗明璋杜国锋

石油机械 2022年5期

徐阳罗明璋杜国锋

(1．长江大学电子信息学院 2.长江大学城市建设学院)

0 引言

油气长输管道的使用周期长，并且经常需要埋入地下一定深度的土层之中，由于环境腐蚀以及外界冲击等因素形成各种管道缺陷，严重时会导致管道泄漏事故[1-2]。为保证油气输送安全运行，对埋地长输管道进行缺陷监测具有十分重要的意义[3-6]。压电陶瓷换能器既可以用作传感器，又可以用作激励器，采用合适规格的压电陶瓷晶片在管道内激励出超声导波进行缺陷监测，具有效率高、监测范围广等优点，因而得到广泛应用[7]。关于超声导波与管道缺陷之间相互作用问题，国内外学者做了许多研究。D.C.GAZIS[8]首先提出了管道中导波的理论表达式并给出了其通用解。LI D.S.等[9]分析了导波在管道中传播时的多模态特性。沈立华等[10]提出了基于进化规划算法的加载流体管道中的导波频散方程求解方法。

采用超声导波对埋地管道进行缺陷监测时，导波能量会通过管道周围土体向外泄漏并引入更多干扰噪声，很容易淹没管道缺陷对于超声导波的反射回波信号。在管道缺陷监测过程中引入时间反转法，可以有效提高超声导波对管道缺陷的监测能力[11]。法国科学家M.FINK[12]最早提出了时间反转法，它将直接导波法监测得到的缺陷反射回波信号进行时间反转并重新在管道内进行激励，即后到达的信号先激励，先到达的信号后激励，最终形成的时间反转导波将同时到达缺陷处，使导波能量在缺陷位置发生聚焦，从而增强缺陷反射回波的幅值。时间反转法已经在许多领域获得应用并取得了大量研究成果[13-14]。本文对埋地管道中超声导波的传播特性进行分析，通过现场试验研究了采用时间反转法提高超声导波对埋地管道缺陷监测能力的可行性。结果表明，利用时间反转导波的时间和空间聚焦效应，可明显增强管道缺陷监测信号的信噪比，使之更容易从干扰噪声中进行提取、分析和定位，从而有效提高超声导波对埋地管道缺陷的监测能力。

1 埋地管道中的导波特性

1.1 埋地管道频散方程

超声导波在空心圆管中传播时，质点位移满足Navier运动方程[15]：

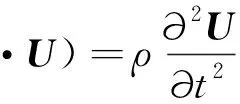
(1)

式中:U为包含径向r、周向θ和轴向z 3个方向的位移矢量,λ和μ为材料的拉姆常数,ρ为材料密度,t为时间,∇为拉普拉斯算子。

位移矢量U可以被分解为膨胀标量势函数Φ和等容矢量势函数H：

U=∇Φ+∇×H

(2)

对于埋地管道而言，因其与周围土体紧密耦合，使得管道中传播的超声导波能量有一部分泄漏到周围土体中，在这种情况下进行管道缺陷监测时，传感器接收到的缺陷反射回波信号将有部分能量损失[16]。因此对于沿埋地管道轴向传播的纵向导波，在理论分析时需要在势函数中附加一个位移场方程:

uz=Aei(kz-ωt)e-α′

(3)

式中:uz为附加的轴向位移场，A为位移场的初始振幅，k为波数，ω为波的圆周率，α′为土体的衰减系数。

Hankel函数所特有的渐进性可以用来表征超声导波通过管道周围土体向外扩散并逐渐衰减消失的特性。可以在Navier运动方程的标量势函数中引入第二类Hankel函数来模拟超声导波的衰减，其表达式为：

(4)

(5)

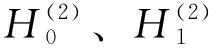
将Hankel函数代入应力及位移表达式中，化简后可以得到：

(6)

式中:σrr′、σrz′分别为埋地管道的径向和轴向应力，ur′、uz′分别为埋地管道的径向和轴向位移，λ′和μ′为土体的拉姆常数，β′为波扩散到土体中的入射角。

我钱永根，1981年生于浙江绍兴。现为杭州画院专职画师、办公室副主任，浙江省美术家协会会员，杭州市美术家协会副秘书长。

管道内表面上的应力满足边界条件：

σrr(a)=σrz(a)=0

(7)

式中:上标a表示管道的内表面。

管道外表面与周围土体接触面上的位移和应力满足边界条件：

(8)

式中：上标b表示管道的外表面，上标s表示土体。

将式(6)～式(8)联立为方程组，要使方程组有非零解，其系数行列式必须为0，即有：

|Cij|6×6=0 (i，j=1，2，……，6)

(9)

式(9)即为埋地管道中超声导波纵向模态的频散方程，是一个6×6行列式，其中各个元素与波数和频率有关。

1.2 埋地管道群速度频散曲线

埋地管道中超声导波的频散方程是一种超越方程，对它进行数值求解可以得到埋地管道的频散曲线。

图1所示为埋入地下1 500 mm土层中外径76 mm、壁厚4 mm的AISI 304不锈钢管的群速度频散曲线。

图1 埋地管道的群速度频散曲线Fig.1 Group velocity dispersion curve of buried pipelines

从图1可以看到，在频率为0～150 kHz范围内出现了L(0，1)、L(0，2)和L(0，3) 3种模态导波。其中L(0，2)模态导波的群速度在60～90 kHz频率范围内达到峰值且变化不大，说明其频散程度较小，因此采用L(0，2)模态导波来进行埋地管道缺陷监测可以取得较好的效果。

2 埋地管道超声导波监测现场试验

2.1 埋地管道与试验仪器组成

将一根外径76 mm、壁厚4 mm、长2 000 mm的无缺陷不锈钢管埋入深1 500 mm的土层中，在管道端部沿圆周方向均匀布置2个压电陶瓷换能器阵列，用于激励和接收管道中的超声导波，每个换能器阵列分别由16片压电陶瓷晶片组成。

试验仪器包括MSO2014数字存储示波器、SDG2122任意波形发生器、ATA2021H功率放大器以及用于信号处理的计算机等。

2.2 埋地管道超声导波传播试验

由任意波形发生器产生80 kHz的Hanning窗调制10周期正弦波信号，经功率放大器放大到100 Vpp，加载到管道端部的压电陶瓷激励换能器阵列，激励出管道内的超声导波，并由布置在管道同一端的压电陶瓷接收换能器阵列监测管道中超声导波传播信号，得到如图2所示埋地管道超声导波传播试验轴向位移时程曲线。

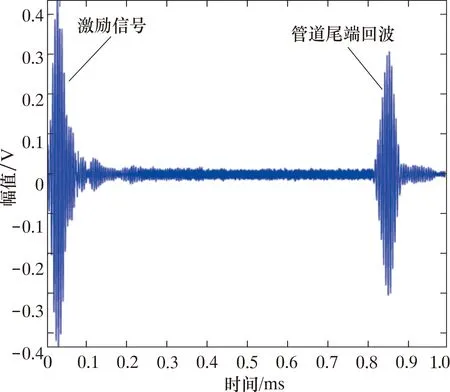
图2 无缺陷埋地管道在80 kHz激励频率下的超声导波传播试验轴向位移时程曲线Fig.2 Axial displacement time-history curve of ultrasonicguided wave propagation test of defect-free buriedpipeline at 80 kHz excitation frequency

通过计算激励信号波包与管道尾端回波波包之间的时间差，得出超声导波在埋地管道中的传播时间约为0.822 ms，已知管道长度为2 000 mm，计算出超声导波在该埋地管道中的传播速度约为4 865.68 m/s。根据前面推导的埋地管道频散方程，计算出超声导波传播速度的理论值为4 911.25 m/s，二者之间的误差为0.93%。

为了进一步检验试验结果的有效性，将激励信号中心频率从60 kHz开始，以步长10 kHz逐步增加到100 kHz，试验测量值与理论计算值如表1所示。根据表1绘制出二者对比曲线，如图3所示，其中小圆点表示试验测量数据，蓝色实线为埋地管道理论频散曲线。由图3可见，在60～100 kHz范围内，试验测量值与理论计算值相差很小，验证了前面理论推导方法切实可行，据此绘制的频散曲线具有一定实用指导意义，同时说明沿管道端部圆周方向均匀布置的压电陶瓷换能器阵列能够激励出埋地管道中的L(0，2)模态导波。

表1 埋地管道中超声导波传播速度试验测量值与理论计算值Table 1 Test measurements and theoretical calculations ofpropagation velocity of ultrasonic guidedwaves in buried pipelines

图3 埋地管道中L(0，2)模态导波的理论群速度与试验测量值对比图Fig.3 Comparison of group velocities between theoretical calculations and test measurements of L (0，2)mode guided wave in buried pipelines

3 埋地管道缺陷监测结果分析

另取一根相同尺寸的不锈钢管，在管道端部沿圆周方向均匀布置2个压电陶瓷换能器阵列。距离导波激励端1 000 mm处加工一个槽形周向裂纹缺陷，缺陷周向长度35 mm，轴向宽度2 mm，深度1 mm；距离导波激励端1 500 mm处加工一个贯穿的圆孔形缺陷，圆孔直径2 mm。槽形裂纹缺陷中心与圆孔缺陷中心之间的圆周位置相差180°。

将上述带缺陷的管道埋入地下深1 500 mm的土层中，采用中心频率 80 kHz的Hanning窗调制10周期正弦波作为激励信号，加载到管道端部的压电陶瓷激励换能器阵列，激励出管道中的L(0，2)模态导波进行缺陷监测。图4表示从管道端部接收换能器阵列中单个压电陶瓷晶片上获得的直接导波监测信号。由图4可见，信号波包较为复杂，除了管道缺陷对于L(0，2)模态的反射回波之外，还包含有F(n，m)弯曲模态等转换模态信号以及大量干扰噪声。将沿管道圆周均匀布置的压电陶瓷换能器阵列中所有接收换能器获得的信号进行叠加，可以消除F(n，m)弯曲模态的影响[17]。图5所示为对16个压电陶瓷接收换能器获得的信号进行叠加之后，得到的带有双缺陷埋地管道直接导波监测的试验轴向位移时程曲线。由图5可见，采用直接导波法对埋地管道进行缺陷监测时，缺陷反射回波信号幅值较小，容易与干扰噪声混淆，不易识别。

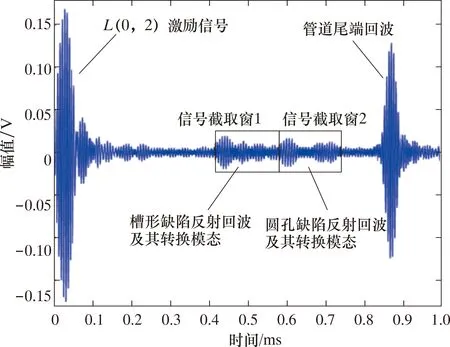
图4 单个接收换能器上的直接导波监测试验信号Fig.4 Direct guided wave monitoring test signals ona single receiving transducer

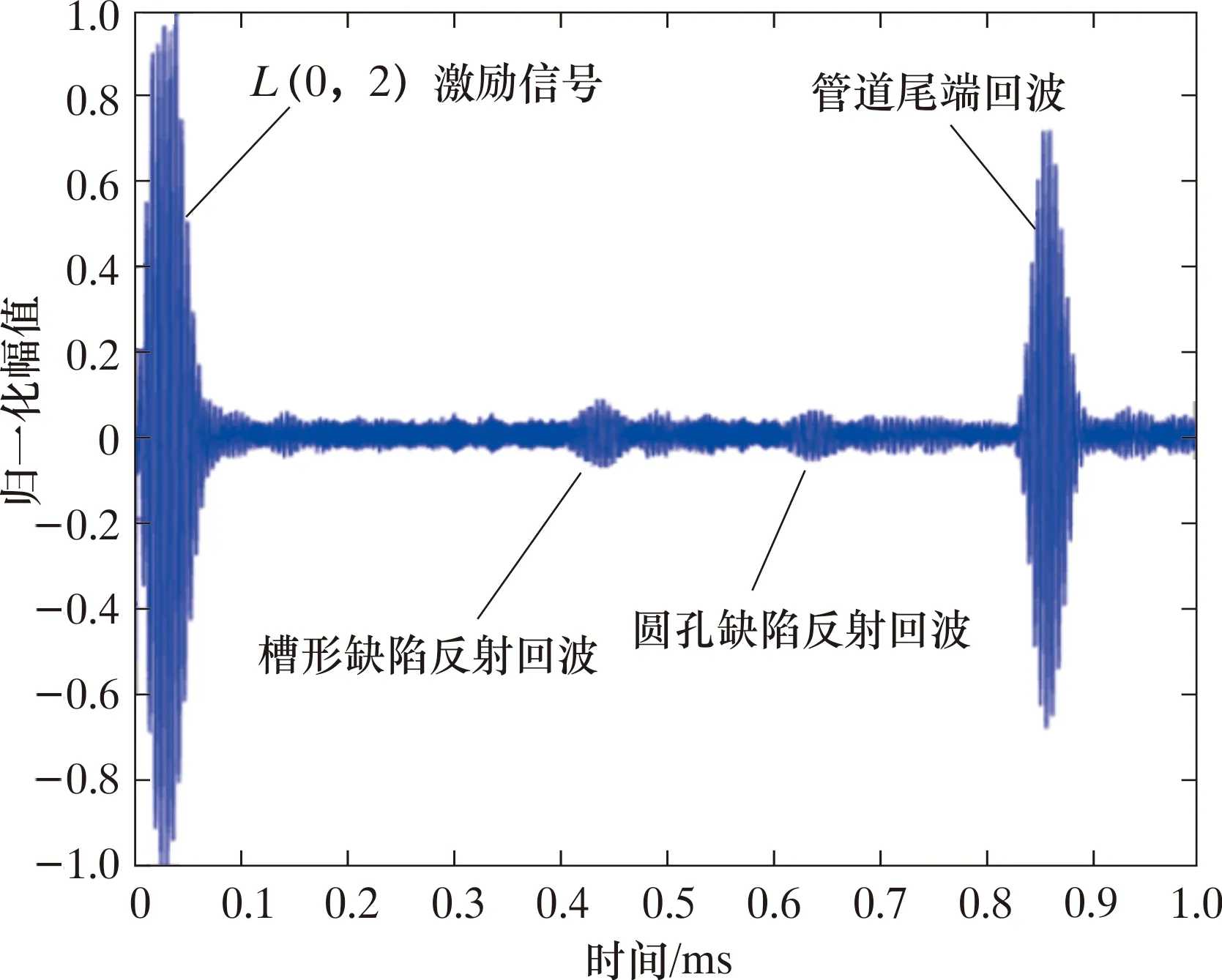
图5 双缺陷埋地管道直接导波监测的轴向位移时程曲线Fig.5 Axial displacement time-history curve monitored bydirect guided waves in buried pipelines with double defects

下面采用时间反转法重新对埋地管道进行缺陷监测。如图4所示，在保证时间起点一致的前提下，先用宽度为0.15 ms的信号截取窗1从16个接收换能器获得的直接导波监测试验信号中，截取出前面的槽形缺陷反射回波及其转换模态信号f(t)1并进行时间反转，生成16个时间反转信号fTR(t)1，两组信号满足fTR(t)1=f(τ-t)1，其中τ为信号截取矩形窗的宽度。将这16个时间反转信号fTR(t)1分别加载到埋地管道端部相应的激励换能器上重新激励，每激励一次同时记录16个接收换能器上的轴向位移时程信号，最后将接收到的16×16个轴向位移时程信号叠加，得到如图6所示的采用槽形缺陷时间反转信号监测的轴向位移时程曲线。

图6 槽形缺陷时间反转监测轴向位移时程曲线Fig.6 Axial displacement time-history curvemonitored by time reversal method in buriedpipelines with groove defects

从图6可以看到，截取前面的槽形缺陷反射回波，及其转换模态所生成的时间反转信号在埋地管道内重新激励之后，导波能量将在前面槽形缺陷位置处发生聚焦，使得槽形缺陷的反射回波信号幅值明显增大，更容易从轴向位移时程曲线中识别。

再用相同宽度的信号截取窗2以同样的方法，截取出后面的圆孔缺陷反射回波及其转换模态信号f(t)2，进行时间反转之后，生成16个时间反转信号fTR(t)2。将这些时间反转信号fTR(t)2通过管道端部相应的激励换能器重新激励，每激励一次同时记录16个接收换能器上的轴向位移时程信号，最后将接收到的16×16个轴向位移时程信号进行叠加，得到如图7所示的采用圆孔缺陷时间反转信号监测的轴向位移时程曲线。由图7可见，截取后面圆孔缺陷反射回波及其转换模态所生成的时间反转信号，在埋地管道内重新激励之后，大部分导波能量将绕过前面槽形缺陷而在后面圆孔缺陷处发生聚焦，使得圆孔缺陷反射回波信号幅值明显增大，更容易辨识。

图7 圆孔缺陷时间反转监测的轴向位移时程曲线Fig.7 Axial displacement time-history curvemonitored by time reversal method in buriedpipelines with round hole defects

从图6和图7所示缺陷轴向位移时程曲线上获取激励信号和缺陷反射回波信号的到达时间，再根据缺陷监测试验中实际测得的超声导波群速度，很容易确定管道缺陷的轴向位置。由于时间反转导波能量在管道缺陷位置处发生聚焦，所以分别从槽形缺陷和圆孔缺陷所对应的16个接收换能器轴向位移时程曲线中，截取缺陷反射回波并计算出它们的极大值，按顺序绘制极坐标图，得到不同缺陷轴向位移圆周分布曲线，根据曲线中的最大值即可确定管道周向不同时钟方位缺陷的中心位置，如图8所示。

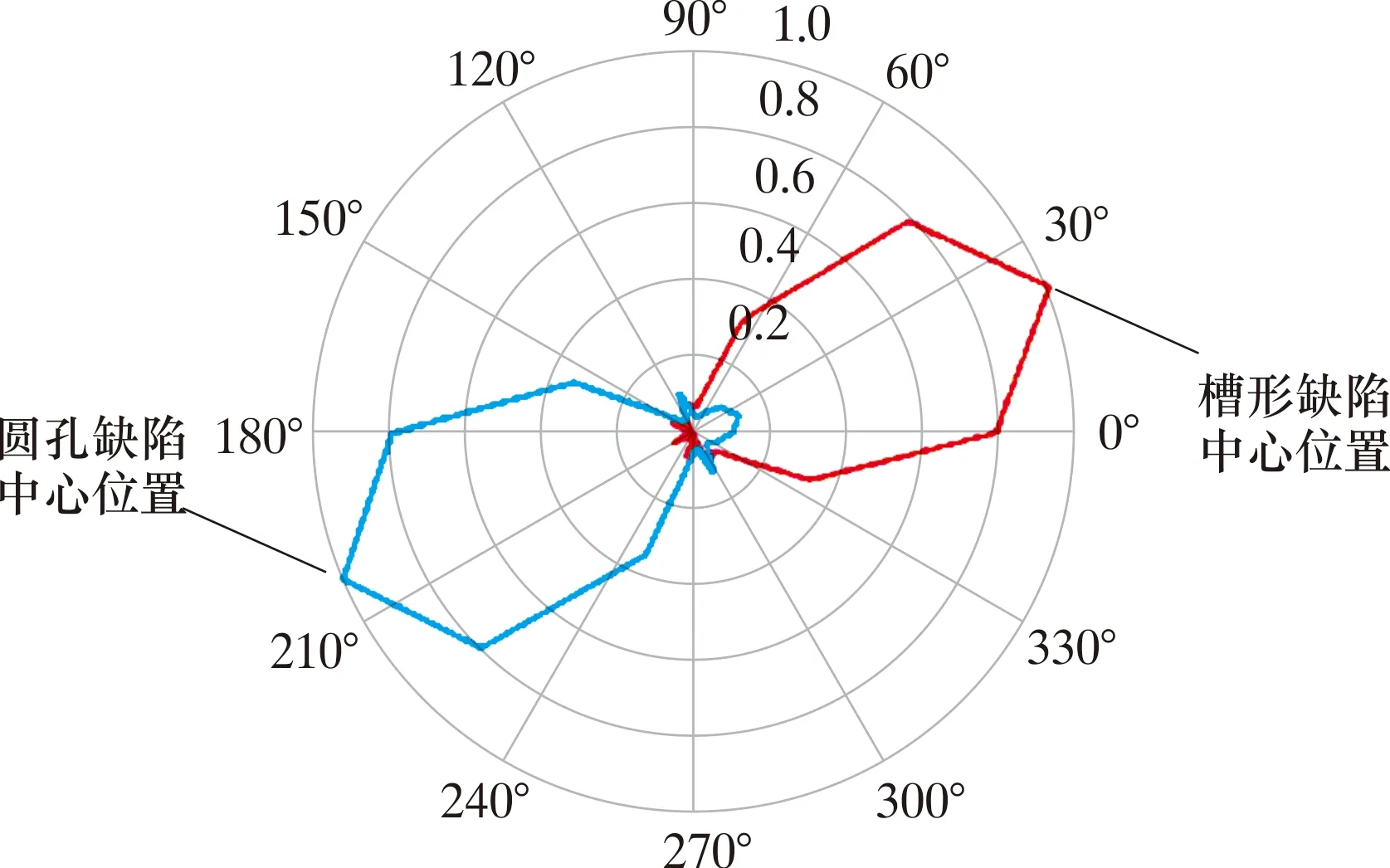
图8 埋地管道上双缺陷的轴向位移圆周分布曲线Fig.8 Circumferential distribution curve of axialdisplacement of double defects in buried pipelines

由上述试验结果可以看到，埋地管道周围土体影响超声导波在管道内的传播，产生更多环境噪声。采用直接导波法进行埋地管道缺陷监测时信噪比较低，缺陷反射回波容易被干扰噪声所淹没，不易识别。而采用时间反转法对埋地管道进行超声导波缺陷监测时，由于时间反转导波具有时间和空间聚焦效应，导波能量将在埋地管道缺陷位置处发生聚焦，使缺陷反射回波信号幅值明显增强，有利于从大量干扰噪声中对缺陷监测信号进行分辨、采集和定位处理，特别是对于埋地管道在损伤初期所形成的小缺陷，采用时间反转法进行超声导波监测可以有效提高管道缺陷监测能力。