基于SPH方法的组合射流破岩模拟研究*
2022-05-10廖翔云马小晶周新超齐思维李宏煜
廖翔云 马小晶 周新超 齐思维 李宏煜
(新疆大学电气工程学院)
0 引 言
页岩气储层普遍具有低渗透的特性,为了大规模开采,必须改善其储层渗透性[1-2]。水力压裂技术有利于提高油气层渗透率,在低渗透油藏的高效开采领域有着较好的应用前景[3-5]。
在计算机理论与技术发展的背景下,数值模拟方法已成为研究水力压裂技术的有效手段之一。雷光宇等[6]运用有限元方法,研究了不同井深条件下射流速度对破岩效率的影响;蒋斌等[7]采用ALE方法对水射流破土进行数值模拟,分析了淹没条件及非淹没条件下冲坑演化的差异。然而,基于网格的数值模拟方法在处理大变形和高应变率的射流破岩问题时,网格会发生扭曲和畸变,使求解精度降低,甚至导致计算终止。因此,研究并采用一种合理有效的数值模拟方法,对实现射流破岩的准确模拟,以及找到影响破岩效果的主要因素十分必要。
目前,无网格方法逐渐受到国内外研究学者的广泛关注[8-9]。光滑粒子流体动力学(SPH)方法作为典型的无网格法之一,运用可运动的粒子离散所求解的计算域,适合模拟变形边界和大变形的问题[10]。司鹄等[11]采用SPH方法分析了脉冲射流破岩过程中应力波的形成、传播及衰减特性。赵健等[12]采用SPH方法研究并得到了粒子射流参数对破岩体积的影响规律。
组合射流作为常用的水射流钻进技术,在超短半径转向钻孔方面优势显著。目前,已有学者对组合射流破岩过程展开了研究[13],揭示了组合射流冲击破岩机理,但对于组合射流破岩能力与射流参数关系的探究还相对较少。鉴于此,本文基于SPH方法构建了组合射流破岩模型,模拟研究了射流参数(射流喷距、射流直径和射流轴向倾角)对组合射流破岩能力的影响。研究结果可为实际工程应用提供一定的理论依据。
1 SPH方法基本理论
SPH方法是一种以插值理论为基础的纯拉格朗日方法。对于本文所研究的问题,将水射流和岩石离散成一系列携带各种物理量的可自由运动的粒子,以求解各种边界条件下的偏微分方程,因此任一宏观变量可由一组离散点的值得到积分插值。利用近似法将偏微分方程转换成积分形式的方程[14-15]:
(1)
式中:Ω为整个求解区域;W(x-x′,h)为光滑核函数;h为粒子的光滑长度,决定支持域的大小;x-x′为空间点与所求场函数值点之间的距离。
利用粒子近似法将连续积分方程(1)转换成离散形式的方程:
(2)
式中:mj为粒子j的质量,ρj为粒子j的密度。
本文采用较为常用的三次B样条核函数[16]:
(3)
式中:C是由空间维度确定的标准化常量,由归一化条件确定,C取1/(πh3)。
2 射流破岩模型的建立及参数设置
针对研究的组合射流冲蚀岩石的问题,做出如下基本假设:忽略气相因素对水射流的影响,水射流无散射现象;岩石为连续介质,孔隙和裂纹等不影响组合射流破岩;整个射流破岩过程中只涉及水和岩石两种物质。
2.1 组合射流模型
水射流采用MAT_NULL本构模型,将其视为完全塑性材料,赋予其Gruneisen状态方程[17],即有:

(4)
式中:p为冲击压力,a为一阶体积修正量,γ0为Gruneisen常数,c为冲击波速度-质点速度曲线的截距,E为单位体积内能,μ为流体黏性系数,S1、S2和S3为冲击波与质点速度变化曲线的斜率。
水的本构参数为:ρ0=1 050 kg/m3,c=1 647 m/s,S1=1.921,S2=-0.096,S3=0,γ0=0.35,a=0,E=0。
2.2 岩石模型
为了满足大变形、高应变率和高拉压效应的岩石工况假设需要,本文引入该模型对岩石进行描述。H-J-C本构模型综合考虑了岩石材料损伤、应变率和静水压力对屈服力的影响,其强度以规范化等效应力描述为[18]:
(5)

损伤度计算如下:
(6)

其中,页岩参数为:ρ=2 440 kg/m3,A=0.79,B=1.6,C1=0.007,N=0.6。
2.3 几何模型及边界条件

图1 组合射流冲蚀岩石模型Fig.1 Model of rock breaking by combined jets
3 破损坑指标的定义
为了合理描述组合射流冲蚀岩石的破损效果,本文对破损坑进行了特征提取,定义破损坑指标并进行无量纲化处理,分别为:坑纵截面面积(a/A)、表面坑径(w/W)和最大坑深(h/H)。破损坑指标参数示意图如图2所示,其中a、w和h分别为破损坑纵截面面积、表面坑径和最大坑深,A、W和H分别为岩石初始的纵截面面积、宽度和高度。

图2 破岩指标参数示意图Fig.2 Diagram of rock breaking index parameters
4 计算结果分析
4.1 验证模型有效性
为了验证所建模型的有效性,本文对周哲[13]研究的组合射流冲击破岩的动态过程进行了模拟,所取参数与该研究保持一致,射流直径D1为0.8 mm,轴向偏角β为12°,射流间距d为2 mm,初速度v为245 m/s。图3是组合射流冲击破岩过程中破损坑及应力波的演化情况。
由图3可知,在时间t为0.01 ms时,射流冲击岩石表面产生极大的瞬时接触应力并出现破损坑,此时中心射流与边射流冲击形成的破碎坑间有凸台。应力波以接触处为中心呈球形波向四周传播,随着冲蚀时间的延续,应力波扩散至整个岩体,同时中心射流与边射流之间的凸台导通,形成联合破碎坑。

图4表示0.05 ms时岩石纵截面的破损坑情况以及周哲[13]研究所得的岩石CT扫描试验结果。
由图4可知,该模型的模拟结果与CT扫描试验结果的破损坑形状非常接近,从而验证了本研究所构建的组合射流冲蚀岩石数值模型的有效性与合理性。

图4 仿真结果与试验结果对比图Fig.4 Comparison between simulation results and experimental results
4.2 射流喷距的影响
射流喷距是影响组合射流破岩能力的重要因素之一,模拟研究中射流喷距l取1~5 mm,射流直径D1为1.2 mm,射流轴向倾角β为4°,射流间距d为2 mm。
图5表示射流速度v为550 m/s时不同射流喷距下岩石的破损图。从图5可以看出,当射流喷距l≤4 mm时,随着射流喷距的增大,破损坑纵截面面积不断增大,即破岩能力增强;但是当射流喷距l≥5 mm时,岩石破损坑底部的凸台较为明显。为了进一步分析射流喷距对破岩效果的影响,图6给出了不同射流速度下射流喷距与岩石破损坑纵截面面积、最大坑深及表面坑径的变化曲线。
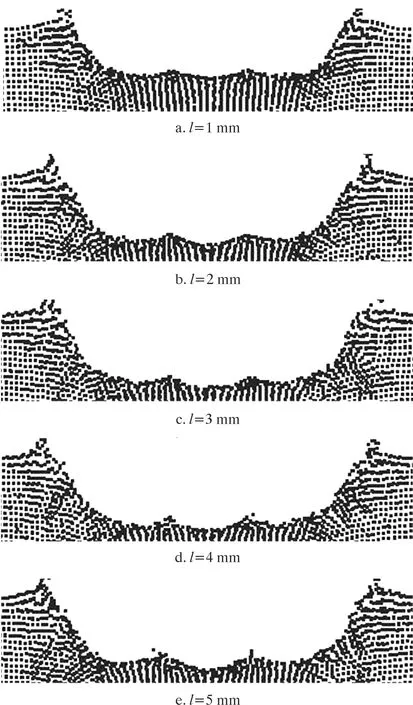
图5 不同射流喷距下岩石的破损图(t=0.05 ms)Fig.5 Rock damage under different jet distances(t=0.05 ms)

图6 不同射流喷距下岩石破损坑指标变化曲线(t=0.05 ms)Fig.6 Variation of rock damage pit index under different jet distances (t=0.05 ms)
从图6可以看出,随着射流喷距的增大,岩石破损坑纵截面面积和最大坑深呈先急剧增大后减小的趋势。这是因为当射流喷距较小时,射流冲击岩石产生的回流会造成干扰,消耗射流的冲击能量,使得破损坑纵截面面积较小;随着射流喷距的增大,回流对射流的干扰作用逐渐减弱,从而破损坑纵截面面积不断增大;但当射流喷距过大时,射流与岩石表面接触时的间距过大,应力波干涉作用减弱,使得破岩效果减弱。由此可知:射流喷距存在一个使得岩石破损效果最大的最优值范围,该最优数值范围为3~5 mm。当射流喷距增加时,岩石表面坑径先增大后减小,特别是在射流速度大于250 m/s后,岩石表面坑径急剧增大,这也说明增大射流速度能够提高岩石的破碎效率。
4.3 射流直径的影响
射流直径也会影响组合射流的破岩能力,模拟中射流直径D1取0.8~2.0 mm,射流喷距l为1 mm,射流轴向倾角β为4°,射流间距d为2 mm(研究中保持射流粒子数大致相同,相差小于2%,因此忽略射流粒子数对研究结果的影响)。图7表示射流速度v为550 m/s时不同射流直径下岩石的破损图。

图7 不同射流直径下岩石的破损图(t=0.05 ms)Fig.7 Rock damage under different jet diameters (t=0.05 ms)
从图7可以看出,射流直径的大小会显著影响岩石破损坑形状,直径较小时,岩石破损坑底部的凸台较为明显,随着射流直径的增大,凸台逐渐消失,破损坑形状逐渐趋于弧形。为了进一步分析射流直径对破岩效果的影响,图8给出了不同射流速度下射流直径与岩石破损坑纵截面面积、最大坑深及表面坑径的变化曲线。
从图8a可得,岩石破损坑纵截面面积随着射流直径的增大而不断增大,且增大射流速度会使得破损面积的增幅变大。由图8b可知,在不同射流速度下,射流直径的大小对破岩最大坑深的变化影响较小,尤其是在射流速度较低时,其变化甚微,因此射流速度是影响破岩最大坑深的主要因素。由图8c可知,当射流直径增加时,岩石表面坑径先增大后减小。这说明射流直径过大时,由于相邻射流间距较小,射流冲击过程中相互干扰消耗能量,造成破岩坑径减小。因此应当合理选择射流直径,以达到最佳破岩效果。

图8 不同射流直径下岩石破损坑指标变化曲线(t=0.05 ms)Fig.8 Variation of rock damage pit index under different jet diameters (t=0.05 ms)
4.4 射流轴向倾角的影响
本文模拟研究了射流轴向倾角对破岩效果的影响,研究中射流轴向倾角β取2°~10°,射流喷距l为1 mm,射流直径D1为1.2 mm,射流间距d为2 mm。图9表示射流速度v为550 m/s时不同射流轴向倾角下岩石的破损图。
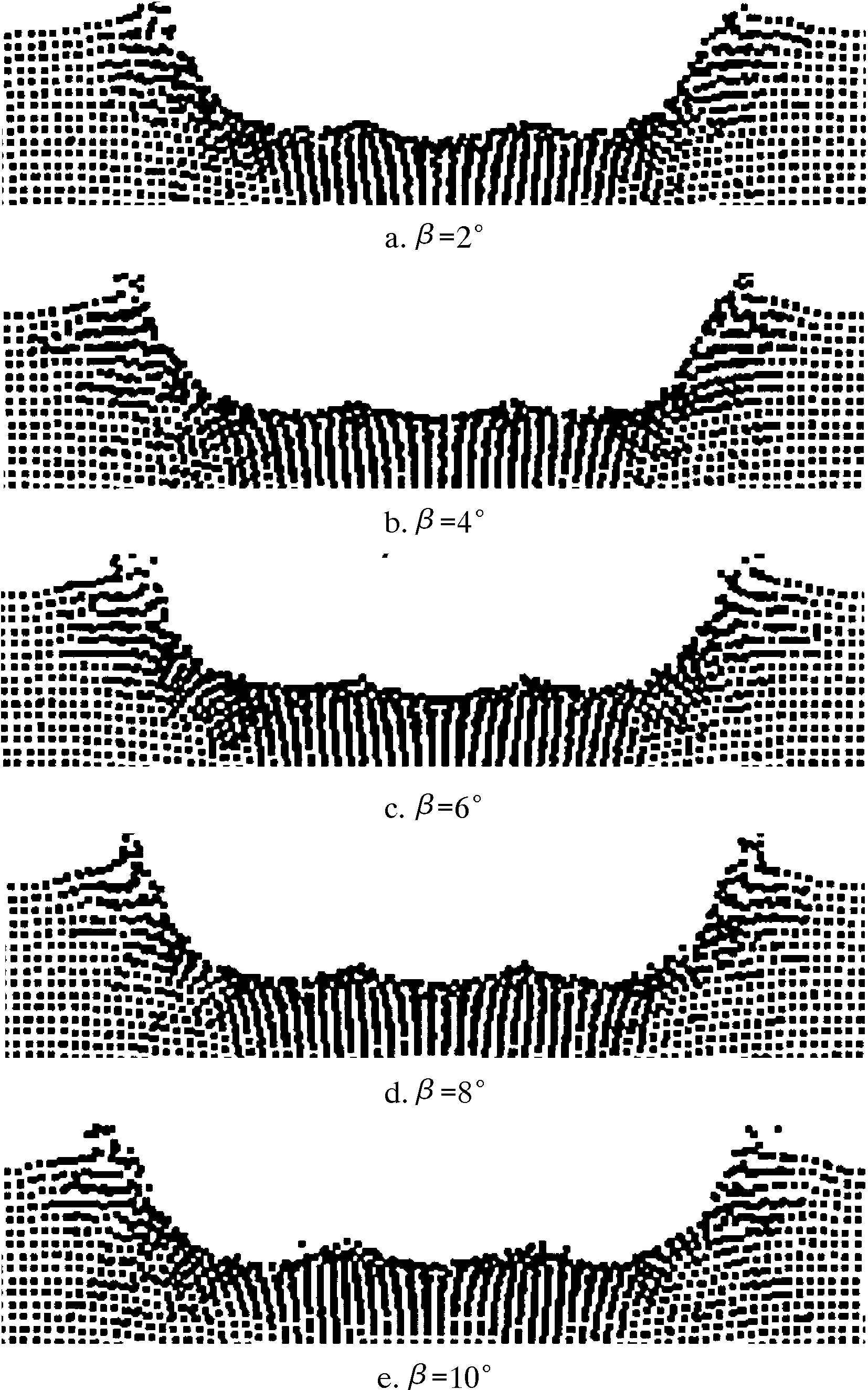
图9 不同射流轴向倾角下岩石的破损图(t=0.05 ms)Fig.9 Rock damage under different jet axial inclinations (t=0.05 ms)
由图9可知,当射流轴向倾角增加时,射流作用范围增大,造成岩石表面坑径不断增大,射流冲击区域形成了联合破碎坑。为了进一步分析射流轴向倾角对破岩效果的影响,图10给出了不同射流速度下射流轴向倾角与岩石破损坑纵截面面积、最大坑深及表面坑径的变化曲线。
从图10a可以看出,射流轴向倾角的变化对破损坑纵截面面积的影响很小,可近似忽略。
由图10b可知,在低速冲击破岩时,射流轴向倾角几乎不会影响破岩深度,但当射流速度增大到一定值时,岩石最大坑深随着射流轴向倾角的增加而减小。
从图10c可得,随着射流轴向倾角的增大,岩石表面坑径不断增大。因此为了扩大岩石表面的破碎面积,合理选择射流轴向倾角十分必要。

图10 不同射流轴向倾角下岩石破损坑 指标变化曲线(t=0.05 ms)Fig.10 Variation of rock damage pit index under different jet axial inclinations (t=0.05 ms)
5 结 论
(1)基于SPH方法构建了组合射流冲蚀岩石的数值模型,通过模拟分析组合射流冲击岩石的动态损伤过程,并与已有研究结果对比,验证了所建模型的有效性。
(2)射流喷距对组合射流破岩能力有着显著影响,破岩效果随着射流喷距的增加而先增大后减小,在本文研究范围内,最优喷距范围为3~5 mm。
(3)射流直径的改变会直接影响岩石破损坑形状,随着射流直径的增大,岩石破损坑纵截面面积不断增大,同时破损坑底部的凸台逐渐消失。
(4)射流轴向倾角会显著影响岩石表面破损情况,随着射流轴向倾角的增加,岩石破损坑纵截面面积变化较小,表面坑径不断增大。
