基于ICEEMD-RAKSVD的地震弱信号去噪方法

朱剑兵

(中国石化 胜利油田分公司物探研究院，东营 257022)

0 引言

众所周知，地震勘探由于噪音来源多，一些弱信号往往会淹没在噪音里，常规方法很难去识别弱信号中的构造、储层信息。为了有效识别弱信号，前人引入了很多方法，其中包括：基于非线性动力系统的混沌理论[1]、基于独立分量分析的盲源分离技术[2]、基于奇异值分解(SVD)的方法[3]、基于经验模式分解(EMD)[4]和基于高阶统计量[5]等识别技术。

Aharon[6]提出了KSVD算法；韩文功等[7]提出的SVD分解方法可以较好进行弱信号的识别和去噪。KSVD算法由于需要进行多次SVD分解的操作,因此，耗时过长, Rubinstein[8]在KSVD的基础上提出了AKSVD算法(Approximate KSVD)，但是其效果比较差；Dumitrescud等[9]在KSVD基础上引入了正则化，得到RKSVD与RAKSVD(正则化近似KSVD)方法,并进行了对比，RAKSVD在效果几乎与KSVD一致的情况下，大大提高了效率。在模态分解去噪方面，Huang等[10]在1998年首次提出了经验模态分解理论(EMD)。然而EMD也并非完美，仍存有一定的缺陷性，诸如部分模态之间的混叠现象、端点效应以及筛分准则等；Wu等[11]引入了总体经验模态分解(EEMD)，对EMD算法进行了的改进，但又出现了新的问题，恢复信号中仍含有一定程度的残余噪音成分，无法将其消除干净；Torres[12]对EEMD算法进行了改进，引入的完备总体经验模态分解(CEEMD)拥有高精度去噪的优势，但也不能盲目去除高频模态，其中还保存着很多有效信息；杨涛[13]结合KSVD和CEEMD的特点，利用KSVD对弱信号的识别优势及CEEMD的高效去噪，设计了一个基于KSVD的CEEMD去噪识别方法，去噪效果较好，但计算效率相对较低。笔者将改进的CEEMD(ICEEMD)与正则化近似KSVD(RAKSVD)有机结合起来，形成了基于ICEEMD-RAKVSD的去噪方法，该方法能够对地震弱信号有效识别，取得了较好的弱信号去噪效果，同时计算效率也得到了提升。

1 RAKSVD方法原理

由于KSVD中每次原子更新都要进行一次SVD分解，从而导致了计算效率较低。Rubinstein等[8]提出了一种近似KSVD算法(AKSVD)，该算法能够明显提高计算效率，但由于引入了近似，SVD分解结果存在一定的误差，因而影响了分解效果。针对这一问题，Irofti等[14]提出了正则化近似KSVD(RAKSVD)算法，建立岭估计模型，解决稀疏分解中的病态问题，从而使SVD分解结果的误差得到很大程度上的控制，提高了稀疏分解效果。

1.1 KSVD字典

KSVD字典是学习型字典之一，具有更适合反映数据结构特点的优势，能获得较好的去噪效果。KSVD算法通过对初始化字典进行逐列更新，用来寻找一个最佳字典的过程，假定训练的信号为Y∈Rm×n，其中m为信号的行数，n为信号的列数，每列对应于一个训练样本。学习型字典模型可以描述为式(1)。

(1)

式中：D∈Rm×p为待学习字典，p为字典的列数；X∈Rp×n为稀疏表示系数；‖·‖0表示l0范数；‖·‖2表示l2范数；T为每列个数的最大值。

首先固定字典D，利用正交匹配追踪算法(OMP)对已知样本数据进行分解，获取初始稀疏分解系数矩阵。

字典更新实施步骤如下：

1)记当前更新的第k列字典原子为dk，X中使用到dk原子的索引集合为Ik。

2)计算残差：

(2)

式中：xj为x的第j列；Ek为去除dk外的残差。

(3)

式中：U表示左奇异矩阵；V表示右奇异矩阵；Λ是奇异值合集；r表示非零奇异值的数量；ui表示左奇异矩阵的第i行；σi表示第i个奇异值；νi表示右奇异矩阵的第i列。

4)原子和稀疏系数更新为：

xk=σ1ν1，dk=u1

(4)

1.2 近似KSVD

Rubinstein等[8]在KSVD的基础上提出了AKSVD算法,主要是在上述步骤3)中采用近似计算更新原子,AKSVD算法更新后的原子和相关系数分别为式(5)和式(6)。

(5)

(6)

1.3 正则化AKSVD

稀疏分解是一种不适定问题,而正则化方法能有效提高分解效果。正则化字典习模型可描述为式(7)。

(7)

式中，μ>0为正则化参数。同样的，记当前更新的字典原子为dk，X中使用到原子的索引集合为Ik，则公式(2)可以变为式(8)。

μ‖Xk,Ik‖2

(8)

由于相关系数里除了第k行外，都为固定项。

由公式(2)则可得到：

(9)

(10)

根据式(10)，从KSVD算法的正则化[9]可以得出，正则化约束后的更新原子方法和原算法一致，而正则化参数是应用到了稀疏系数的更新，使系数变为1/(1+μ)倍，通过给稀疏系数一个权值，每次通过这个权值影响后续的原子更新，最终完成字典的更新。所以RAKSVD的原子和稀疏系数更新[14]为式(11)和式(12)。

(11)

(12)

1.4 效果对比

图1为KSVD、AKSVD、RAKSVD三种训练字典的误差对比图，其中训练集Y的稀疏度为5，字典维数为64*256，正则化参数μ为0.1，整个分解过程重复迭代120次，取平均值得到均方根误差RMSE(单位无量纲)随迭代次数的关系。

图1 误差对比图Fig.1 Error comparison

由图1可以看出，这三种KSVD训练字典在迭代20次后RMSE基本趋于稳定，其中AKSVD训练效果里相对最差，RAKSVD与KSVD训练效果接近，经前人研究AKSVD相比于KSVD效率提高,故而RAKSVD在提高效率的同时，也能达到较好的分解效果。

2 ICEEMD方法原理

首先，EEMD算法在解决EMD存在的模态混叠、端点效应等缺陷的同时，也导致了分解的IMF分量存在噪音残余，而CEEMD通过在不同阶段加入不同高斯白噪音进行调整，比例大小根据待分解信号自适应计算得到，同时每个符合条件的模态分量对应的计算残差值是固定唯一的。不仅解决了模态混叠问题，同时使原始信号复原的精度变得更高。

按照Torres[12]所设计的CEEMD方法步骤对信号做处理，原始信号中各个频率成分的信号，基本上都能够得到较好的分解，但该算法仍存在可能出现虚假模态的问题，同时由于高斯白噪声的加入，分解的模态中会混入一定程度的噪声。为了解决上述问题，改进的CEEMD(Improved CEEMD,ICEEMD)算法重新定义了各个模态局部均值的求取。

假设：Ej(·)为CEEEMD分解得到的第j阶模态,s(t)为原始地震信号，ωi为加入的第i个高斯白噪声，白噪声加入的比例为εk。则改进后的ICEEMD实现步骤如下：

1)将不同正负成对的白噪声分别加入原始信号中，合成得到T个新信号(T为偶数)，计算集合平均得到IMF1(t)。

(13)

2)令r0(t)=s(t)，对k=1、…、K，计算k阶残差rk(t)为式(14)。

rk(t)=rk-1(t)-IMFk(t)

(14)

3)对k阶残差添加不同比例系数的白噪声：rk(t)+εkEk+1(ωi(t))，经EMD分解得到IMF1(t)，计算总体平均并将其作为IMF(k+1)(t)。

(15)

4)重复上述步骤，直到达到迭代条件，得到最终的残差E(t)为式(16)。

(16)

CEEMD去噪往往是直接去除IMF1或IMF1和IMF2分量，但其中往往包含有效信息，所以，虽能有效去除高频噪音，但对于弱信号去噪的问题，容易丢掉真正的有效信号，使同相轴不连续。

相比于CEEMD算法，改进后的CEEMD(ICEEMD)算法可以加入更少的白噪声个数，就能使信号得到很好的模态分离，同时，在相同参数的条件下，ICEEMD分解的效果更好，计算效率更高。

3 去噪方法

KSVD字典稀疏去噪方法是属于对压缩感知原理的改进算法，通过训练样本求取冗余字典，较好地刻画出信号特征，从而更加精确地重构原信号，实现噪声去除和保留有效信号的目标。KSVD字典虽然能将噪音基本压制和消除，但在信号的波峰波谷处仍会存有残留一些毛刺。ICEEMD算法不需要提前设置基函数，它是以信号本身的特点作为基础来自动分解和重构信号，打破了测不准原理的限制，达到了高精度识别弱信号的能力。

具体实现步骤为：

1)利用ICEEMD算法对地震信号进行分解得到固有模态函数集，根据分解效果，将其划分为噪声主导模态、信号主导模态和过渡模态。

2)对于噪声主导模态，则直接舍弃。

3)对于信号主导模态，将其与原始信号叠加，形成主导信号集，通过RAKSVD方法进行主导信号集的分解和去噪。

4)对于过渡模态，先将其叠加，再进行ICEEMD分解；舍弃噪音模态后，与原始信号叠加，重构过渡信号集，通过RAKSVD方法进行过渡信号集的分解和去噪。

5)将步骤3)和步骤4)中的两个分解结果重构并平均，得到最终的去噪结果。

4 模型测试

含有弱信号模型如图2(a)所示，模型共有25道，每道300个采样点，Ricker子波主频25 Hz。在200 ms处有一弱信号。图2(b)为含噪模型，加入噪声后的峰值信噪比(PSNR)为1.2，图2中强轴能够明显看到，但弱轴在噪声的埋没中已经不明显了。对图2(b)分别采用五种算法进行去噪处理，得到的结果如图3所示，图4为模型的15道的单道方法去噪结果，表1是各方法的去噪效果与时间对比。

表1 五种方法针对模型数据的去噪效果对比Tab.1 Comparison of the effects of five methods for denoising the model data

图3 五种方法针对模型数据的去噪结果Fig.3 The result of five methods for denoising the model data(a)KSVD去噪；(b)RAKSVD去噪;(c)CEEMD去噪；(d)CEEMD-KSVD去噪；(e)ICEEMD-RAKSVD去噪

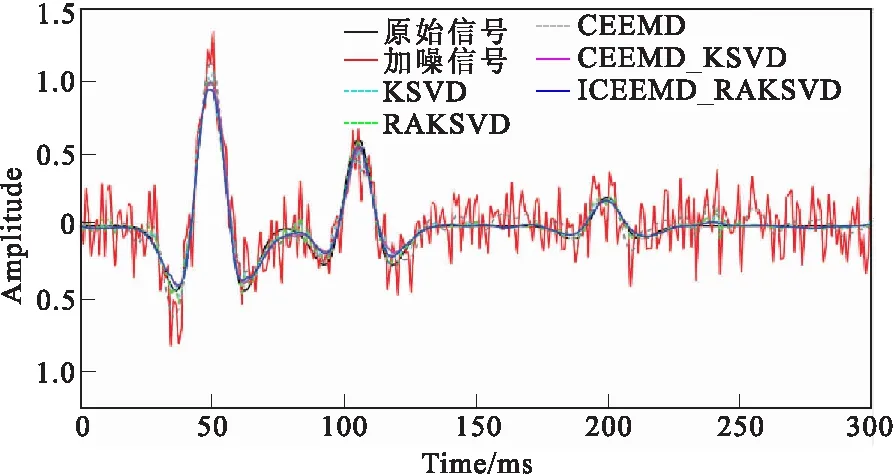
图4 单道去噪方法结果对比Fig.4 Comparison of single channel denoising results

从图3、图4和表1可以看到，如果CEEMD单独使用，则对弱信号的识别和去噪效果最差；KSVD和RAKSVD对模型中弱信号的识别和去噪效果较好，说明该类方法相比于CEEMD，对弱信号识别有着独特的优势，但仍有一些毛刺的残留，在实际应用中，当地下介质不均匀或由薄互层形成复波时，其缺点会被放大；CEEMD-KSVD和ICEEMD-RAKSVD是将模态分解和字典训练联合在一起进行去噪，将模态分解的信号分解为主导模态和过渡模态，利用KSVD和RAKSVD对弱信号识别的优势，最终使含噪弱信号中的噪声得到了较好的压制，且保留了有效弱信号，ICEEMD-RAKSVD方法能够达到最好的去噪效果。由表1可以看到，由于CEEMD算法需要多次迭代，每次迭代需要加入大量成对的高斯白噪声，因此，其计算效率低。KSVD和RAKSVD计算时间少，RAKSVD较KSVD效率提高了60%。由于CEEMD的引入，CEEMD-KSVD和ICEEMD-RAKSVD算法明显增加了计算时间，ICEEMD-RAKSVD 相对于CEEMD-KSVD效率提高6%，对于简单的稀疏模型，CEEMD的计算时间占主导，因此，计算效率提升幅度不是很大。

5 实际资料处理

针对实际资料，对本方法的去噪效果进行了进一步测试。图5(a)为原始局部叠前地震道集，图5中随机噪声十分发育，信噪比非常低，其中弱同相轴不清晰、不连续。上述五种方法的去噪结果如图5(b)～图5(f)所示，图6为单道去噪结果对比展示，图7为去噪后残差剖面效果对比，去噪效果与时间对比见表2。

表2 五种方法针对实际资料的去噪效果对比Tab.2 Comparison of the effects of five methods for denoising the actual data

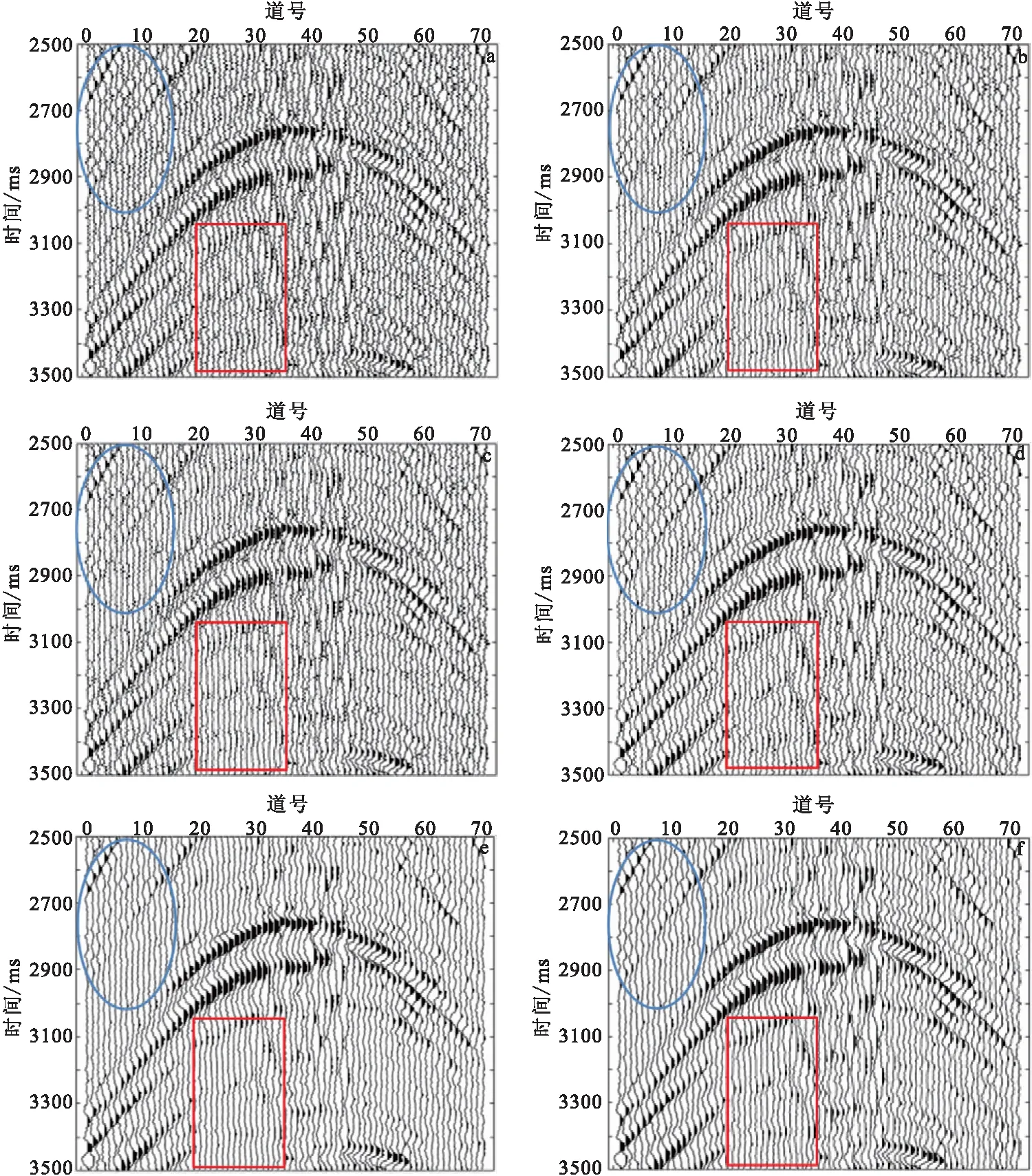
图5 五种方法针对实际资料的去噪结果Fig.5 The result of five methods for denoising the actual data(a)原始叠前地震道集；(b)KSVD去噪；(c)RAKSVD去噪；(d)CEEMD去噪；(e)CEEMD-KSVD去噪；(f)ICEEMD-RAKSVD去噪

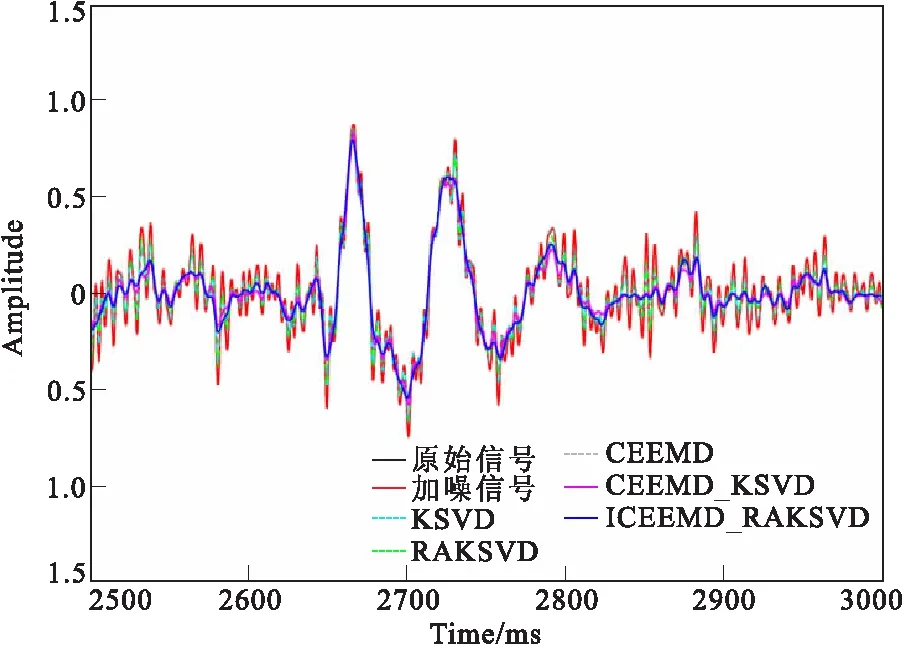
图6 单道去噪方法结果对比Fig.6 Comparison of single channel denoising results

从图5和表2可以看出，对于弱地震信号，实际资料的处理结果与模型测试得到的结论相一致：CEEMD去噪效果较差，去噪后PSNR最低，将部分弱同相轴的有效信号充当噪音去除，弱同相轴损失严重；RAKSVD与KSVD稀疏去噪较明显，但仍存留了许多噪音。CEEMD-KSVD和ICEEMD-RAKSVD算法都能够很好地压制噪声，红方框标记可以看出ICEEMD-RAKSVD有效弱信号得以保留。从图5(a)可以更为清晰看出五种方法对比，而图6可以得出 CEEMD-KSVD和ICEEMD-RAKSVD算法去噪效果几乎一致，能有效去除噪音，图7蓝圆圈中可以看出，CEEMD-KSVD去除的残余还仍然保留些有效信号，而本文方法去除的噪音没有保留有效信号，去噪效果更好，同时由于实际地震数据非常复杂，训练字典的时间大大增加，从表2可以看出，RAKSVD较KSVD计算时间缩短了65%，下降幅度较为明显，ICEEMD-RAKSVD相对于CEEMD-KSVD时间缩短了40%。对实际地震资料的去噪处理，更能突显本文方法在提高计算效率方面的优势。

图7 去噪后残差剖面效果对比Fig.7 Comparison of residual profile effects after denoising(a)CEEMD_KSVD;(b)ICEEMD_RAKSVD

6 总结

由于弱地震信息往往受噪音影响更大，通过去噪能更好地识别弱信号。CEEMD去噪方法直接舍弃高频模态，容易造成高频中有效信息的丢失，而完整地保留了其他含有噪音模态，KSVD去噪方法和RAKSVD去噪方法，对于弱信号的识别效果较好，但去噪后残留毛刺，其中RAKSVD计算效率得到明显提高，CEEMD-KSVD去噪方法能达到较好的去噪效果，但计算效率相对较低，这里指出的基于ICEEMD-RAKSVD去噪方法能在保证较好的去噪效果情况下，还能有效提升了计算效率，在实际地震处理中提升效率尤为重要，该方法具有一定的应用价值。