基于连通性函数的多点地质统计建模参数敏感性分析方法

杜 川, 喻思羽, 李少华, 方 红

(1.长江大学 地球科学学院,武汉 430100；2.中国石油 天然气辽河油田分公司 勘探开发研究院,盘锦 124010)

0 引言

随着多点地质统计学(multi-point statistics， MPS)受到广泛的关注，涌现出许多相对成熟的MPS建模算法。相对于传统的两点地质统计学，多点地质统计学利用训练图像代替变差函数表达地质变量的空间结构性[1]，从中获取更高阶的样本统计量[2],MPS建模优点在于既能够模拟地质体复杂的几何结构，也能忠实于条件数据。Guardiano等[2]提出的首个MPS算法每模拟一个网格节点都需要遍历整个训练图像，计算成本非常高，使得该算法难以实际应用。之后，更好的算法被开发出来改善这些缺点。多点统计技术包括基于象元的建模算法SNESIM[3]、基于样式的建模算法FILTERSIM[4]、SIMPAT[5]、DISPAT[6]、基于直接采样的算法DS[7]、IMPACA[8]、HOSIM[9]、CCSIM[10]、基于图像缝合技术的Image Quilting[11]。这些MPS算法使用不同的方法来读取训练图像、存储信息和复制模式。Mariethoz[12]对这些多点地质建模方法进行了定性比较。多点地质统计学建模已用于许多应用之中，例如常见的在储层地质建模研究领域，利用Simpat模拟河流相储层分布[13]；多点地质统计学在河流相储层建模中的应用[14]；在三角洲相储层建模领域的应用，如多点地质统计学建模方法在复杂叠置样式砂体表征中的应用[15]。

在两点地质统计学建模中，通过变差函数考虑统计数据之间的空间相关性[16]。类似的在多点地质统计学建模过程，需要通过给定的数据事件对训练图像进行扫描来获取一个统计先验模型，相关的统计数据取决于给定数据事件的参数，通过人为的参数调整，找到合适的参数设置是获取良好建模效果的前提，不同的参数不仅影响建模的质量，也涉及CPU及内存开销问题[17]。为此前人也进行了大量的探究，常见的参数敏感性分析，如Liu[18]提供了关于SNESIM参数以及每个参数对模型再现质量和CPU成本的完整指南；Meerschman[19]也为DS直接采样算法做了类似的工作；Honarkhah[6]提出了DISPAT，它对用户提供的参数不太敏感。在该方法中，通过计算不同样板尺寸的图案的平均熵，然后使用所谓的肘形图的拐点，自动选择最佳样板尺寸。Strebelle[20]提出了一种通过优化数据样板的大小来最小化SNESIM的计算成本，同时保持模式再现质量的方法。在该方法中，最小可接受的数据样板大小是通过阈值来选择的，超过该阈值，额外的条件数据不会提高估计的条件概率。Kolbjørnsen[21]开发了一种自动方法来定量确定马尔可夫网格建模中使用的多个网格的最佳数量，该方法使用从训练图像获得的方向相关函数;Bai[22]还提出了一种量化方法来估计SNESIM算法的多个网格的最小数量。它使用由改进的联合计数统计量化的空间关联度来寻找最粗略的尺度，并因此基于模拟尺度应不小于目标尺度的标准来估计多个网格的最小数量。

传统建模参数的评价主要依靠人工识别，即首先给定一组(有序)参数集，使用该参数集里的每个参数模拟一组随机模型，然后通过人工判别优选与训练图像相似度较为合适的模型，以该模型对应的参数作为最优参数。人工识别的精确性取决于建模工作者的经验，具有较强主观性，同时人工识别效率低，不适应于现代自动化生产的需要。为了解决这一问题，我们引入了一种基于连通性函数[23-24]的多点地质统计学建模参数敏感性分析方法，通过计算条件数据下生成的模拟图像的连通性概率曲线，并把训练图像与模拟图像连通性概率曲线之间的相似性用余弦相似度来量化，得到基于连通性函数的空间相关性评价指标与建模参数的关系曲线，通过对量化数据进行分析，找到相似度曲线趋于平缓的拐点值，以此拐点值作为最优参数，大于最优值参数将变得不敏感，模型效果不会随着参数值增加而得到明显改善。

1 连通性计算原理

连通性函数被定义为网格上的两个点属于同一个连接区域的概率[24]，利用连通性函数计算区域化变量指示图的连通性，可以反映区域化变量在某一方向某一距离上连通性概率的变化程度。理论上随机模型与训练图像的连通性差异越小，则表明二者沉积相的空间相关性及位置分布特征越相近，也说明了用于生成该随机模型的建模参数越可靠。Eulogio[25]详细地描述了连通性概率计算原理，其计算原理如下：

图1定义工区网格为矩形G，G的网格节点(或象元)属于子集S(砂岩相)或补集Sc(泥岩相)

G=SUSc

(1)

G的象元取值函数定义为指示函数I(u)

(2)

如果u和u′=u+h属于相同的S，用u⟺u′表示，连通性函数τ(h)定义为属于S的两点连通的概率：

τ(h)=P(u⟺u+h│u,u+h∈S)

(3)

其近似计算公式为式(4)。

(4)

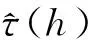
以砂岩相连通性为例，如图1所示u和u′有三种情况，①u和u+h有一个或者两个都属于泥岩相，例如u3与u3+h或者u4与u4+h，则不参与砂岩相连通计算；②u和u+h都是砂岩，但不属于相同砂岩体，例如u2与u2+h，则增加N(u,u+h∈S)数值；③u和u+h都是砂岩，属于相同砂岩体，例如u1与u1+h则增加#N(u⟺u+h│u,u+h∈S)和#N(u,u+h∈S)值。

图1 连通性示意图Fig.1 Schematic diagram of connectivity

2 参数敏感性分析方法

2.1 实现步骤

基于连通性函数的多点地质统计学建模参数优选方法是建立在一个前提条件下：以经典多点算法Snesim的一个重要建模参数--“搜索节点数”为例，基于连通性函数优选搜索节点数；随着搜索节点的增加，随机模型与训练图像的空间相关性、几何形态越来越相似。

在此前提条件下采用有序排列的建模参数集建立一组随机模型集，然后计算基于连通性函数和余弦相似度CosSim函数,评价建模参数集的多点地质统计随机模型与训练图像的空间相关性及结构特征相似性，进而建立基于连通性函数的空间相关性评价指标与建模参数的关系曲线，选取评价指标开始平稳、进入平台区域时的拐点所对应的参数值作为最优参数。

以建模参数“搜索节点数”为例，基于连通性函数的建模参数优选方法具体流程及流程图(图2)如下：

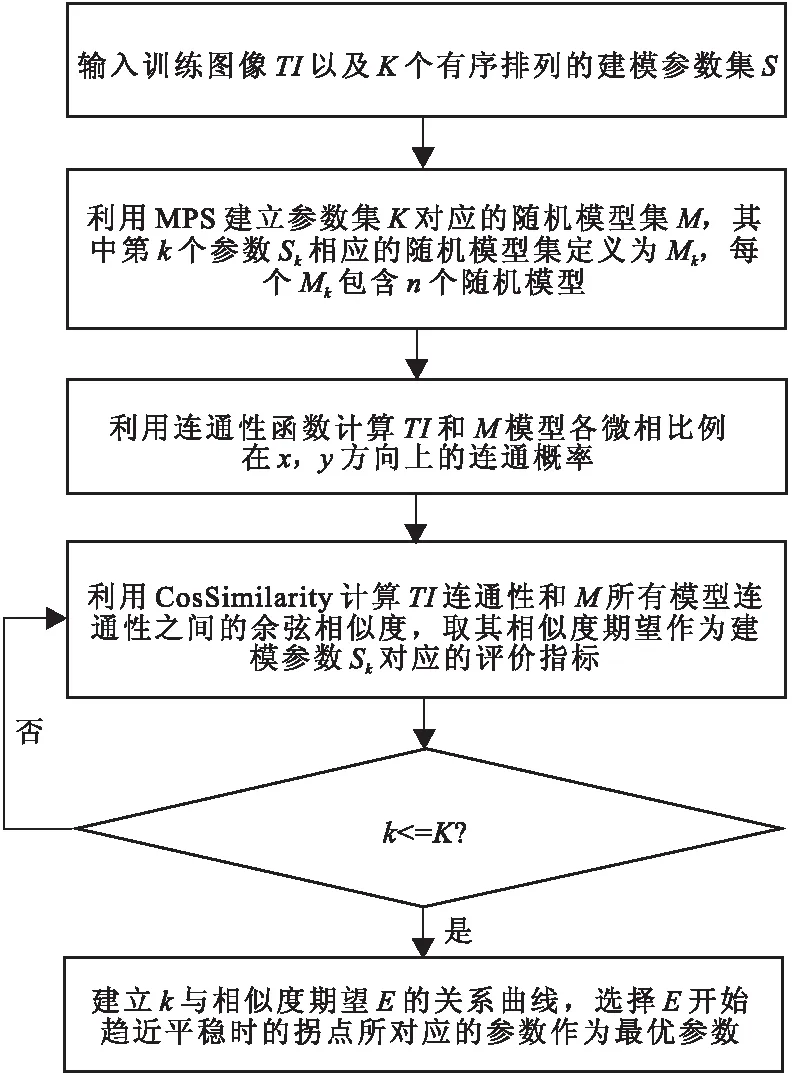
图2 优选方法流程图Fig.2 Flow chart of optimization method

1)输入训练图像TI，给定MPS的关键建模参数——搜索节点的K个连续单调递增数值(例如：1，2，…，K)组成的集合S={1，2，…，K}。

2)采用MPS，使用TI和S生成随机模型集M，其中第k个参数Sk相应的随机模型集定义为Mk，每个Mk包含n个随机模型，则M中共计有N=K×n个模型。

(5)

(6)

计算Mk所有模型与训练图像TI关于连通性函数参数组的余弦相似度，然后取其数学期望作为建模参数Sk对应的空间相关性评价指标ξk

ξk=E[cosθk(Ai,Bi)]

(7)

5)k增加1，如果k小于K-1，则进入步骤4)，否则进入步骤6)。

6)建立参数k与相似度的关系曲线，分析曲线变化趋势，把曲线变化趋于平缓时的拐点建模参数k(i)作为最优参数。随着建模参数值的递增，基于建模参数值的随机模型与训练图像之间相似度逐步增加，并最终达到难以区分的程度，即距离也来越小，相似度越来越高，同时对应的参数越不敏感。

2.2 Snesim建模参数敏感性分析实例

训练图像是地质先验模型，其样式、大小等都会对模拟结果产生重大影响，以一个网状河训练图像channel为例，图3训练图像大小为101×101的网格，黑色部分代表河道砂，白色部分代表背景泥，训练图像数字化的结果是一个101×101的矩阵，“1”代表河道，“0”代表背景泥。其中背景泥占比0.7，河道占比0.3。

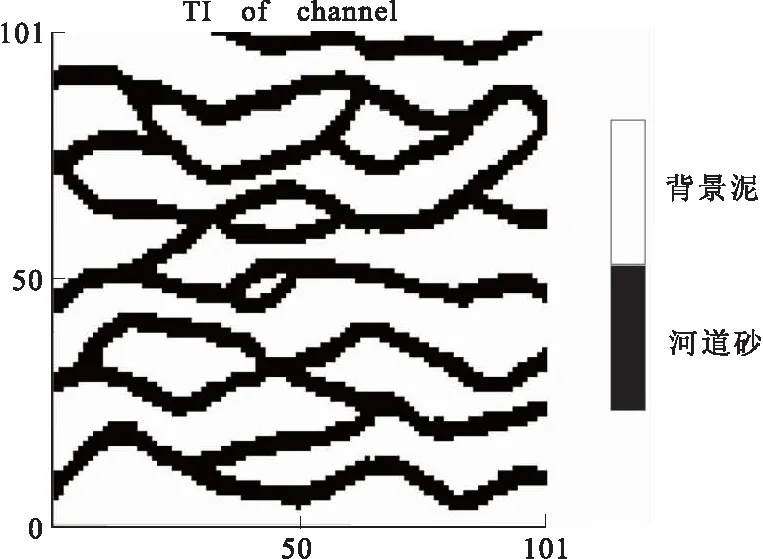
图3 训练图像channelFig.3 Training image channel

2.2.1 搜索节点数

利用Snesim基于像元的多点地质建模对训练图像进行非条件模拟，为了找出最优建模参数值，这个过程中其他参数保持不变，只对Snesim重要建模参数“搜索节点”数进行更改，设置搜索节点数5到75，步长10。其他参数分别设置为：分类变量比例0.7、0.3，伺服器系统参数0.5;搜索半径hx=50，hy=50，搜索角度angel_1=0, angel_2=0，多重网格层数为3。对应每个搜素节点数下进行模拟生成300个随机模型。图4是不同搜索节点数所模拟出来的一个模型(300个实现模型中的一个)，随着搜索节点数量的增加，所模拟出来的河道形态越来越好，与训练图像越来越相似，当增加到25和35以后，设置不同搜索节点数所模拟出来的模型的空间特征相似用肉眼就无法直接区分开来，同时随着搜索节点增加，该参数敏感性降低，所生成的随机模型效果改善不明显甚至几乎难以区分，往往在考虑计算效率以及实现效果上，通过人为肉眼观察给定一个最优参数值往往具有误差，会给建模中带来不确定性。

图4 不同搜索节点数对应的实现模型Fig.4 Implementation models corresponding to different node numbers(a)Node=5;(b)Node=15;(c)Node=25;(d)Node=35;(e)Node=45;(f)Node=55;(g)Node=65;(h)Node=75

根据图2提出的优选方法流程，计算随机模型与训练图像砂岩泥岩相在x、y方向上不同距离下的连通概率，基于连通性概率函数计算公式(4)计算训练图像channel砂岩相泥岩相在x、y方向上的连通概率，图5是训练图像在x和y方向上砂岩泥岩在不同滞后距下的连通概率，随着滞后距的增加砂岩泥岩相在x、y方向上的连通性总体上不断趋于减小，其中砂岩的变化有周期化的上下波动，并且其变化规律能大致反映砂岩的空间分布特征。

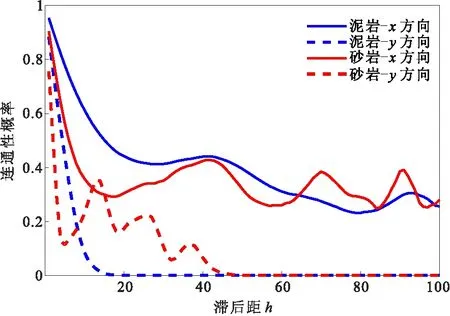
图5 训练图像channel在x、y方向上的连通性概率曲线Fig.5 Connectivity probability curve of training image channel in x and y directions

不同搜索节点所实现的随机模型与训练图像在空间型态结构特征上存在差异，随着搜索节点数量的增加，随机模型的形态结构等特征与训练图像越来越相似，差异会越来越小，这种差异也同时体现在了连通性概率曲线上如图6所示，其中mod1代表搜索节点数等于5的随机模型(绿色)，Mod2是搜索节点数等于75的随机模型(蓝色)，实线与虚线分别代表泥岩相与砂岩相在x或y方向上的连通概率，由图6可知，模型与训练图像的形态特征和空间结构越相似，二者之间的连通性概率曲线就越相近相似。(图6曲线红色和蓝色相近，红色与绿色差异大)

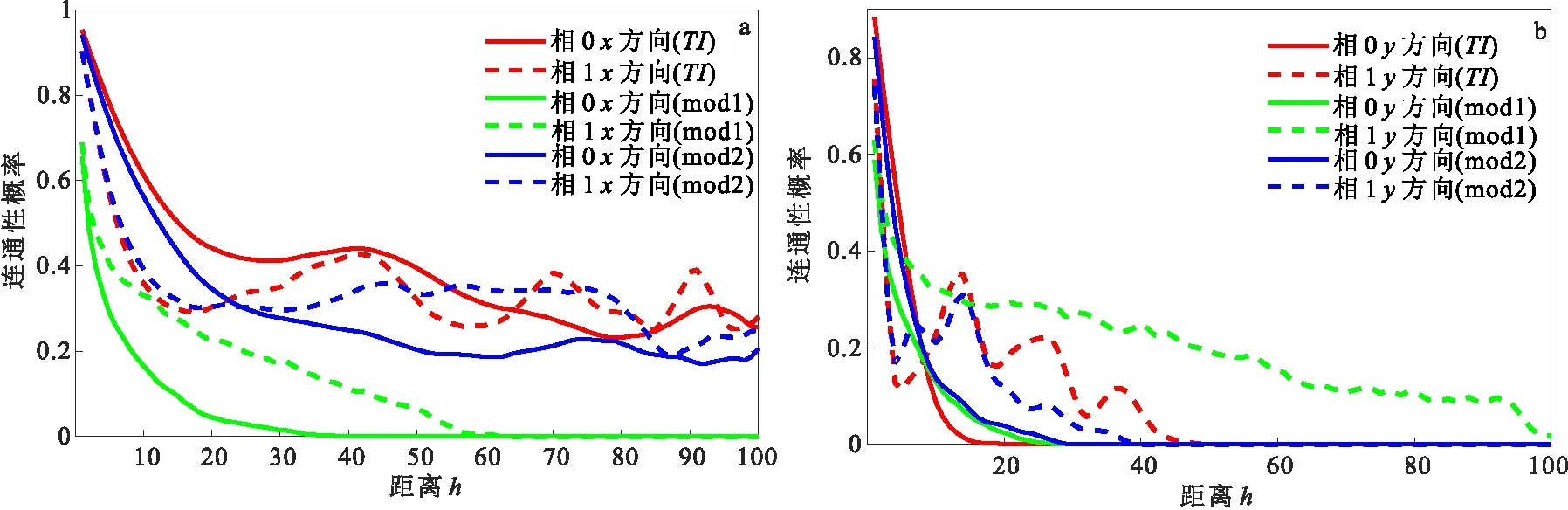
图6 训练图像及其随机模型的连通性概率曲线对比图Fig.6 Comparison of the connectivity probability curves of the training image and its random model(a)x方向；(a)y方向

利用余弦相似度cosSimilarity函数计算训练图像与随机模型连通性概率曲线的相似度，得到随机模型(搜索节点数从5～75)与训练图像关于连通性概率的余弦相似度，然后取其数学期望作为建模参数“搜索节点”对应的空间相关性评价指标ξk建立相似度与搜索节点数的关系曲线(图7)，随着搜索节点数从5开始增加，300个随机模型与训练图像的相似度期望不断增加，表明模型与训练图像越来越相似(根据余弦相似度定义，余弦值越接近1，表示越相似)，当搜索节点数达到35时，空间相关性评价指标进入一个平台区域，参数变得不敏感，模型质量将不再有明显提升，是本例中的优选参数。

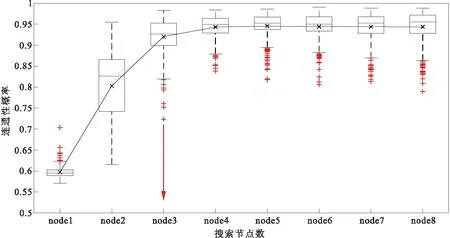
图7 建模参数(搜索节点数)基于连通性函数的余弦相似度变化曲线Fig.7 Cosine similarity change curve based on connectivity function for modeling parameters (node numbers)

2.2.2 多重网格层数

多重网格层数对模拟的效果影响很大，但是随之而来的是消耗更大的计算性能，利用上述分析方法，可以找到一个最优值，既能达到良好建模效果，同时也节约计算性能。对“多重网格重数”这一参数利用相同方法测试，设置多重网格重数从1到8。

保持其他参数不变设置搜索节点数35、分类变量比例0.7、0.3、伺服系统参数0.5，搜索半径hx=50，hy=50、搜索角度angel_1=0, angel_2=0。利用snesim多点地质建模对训练图像进行非条件模拟，在每个多重网格重数下进行模拟生成300个随机模型(图8显示对应网格层数下所模拟的300个实现模型中的一个)。

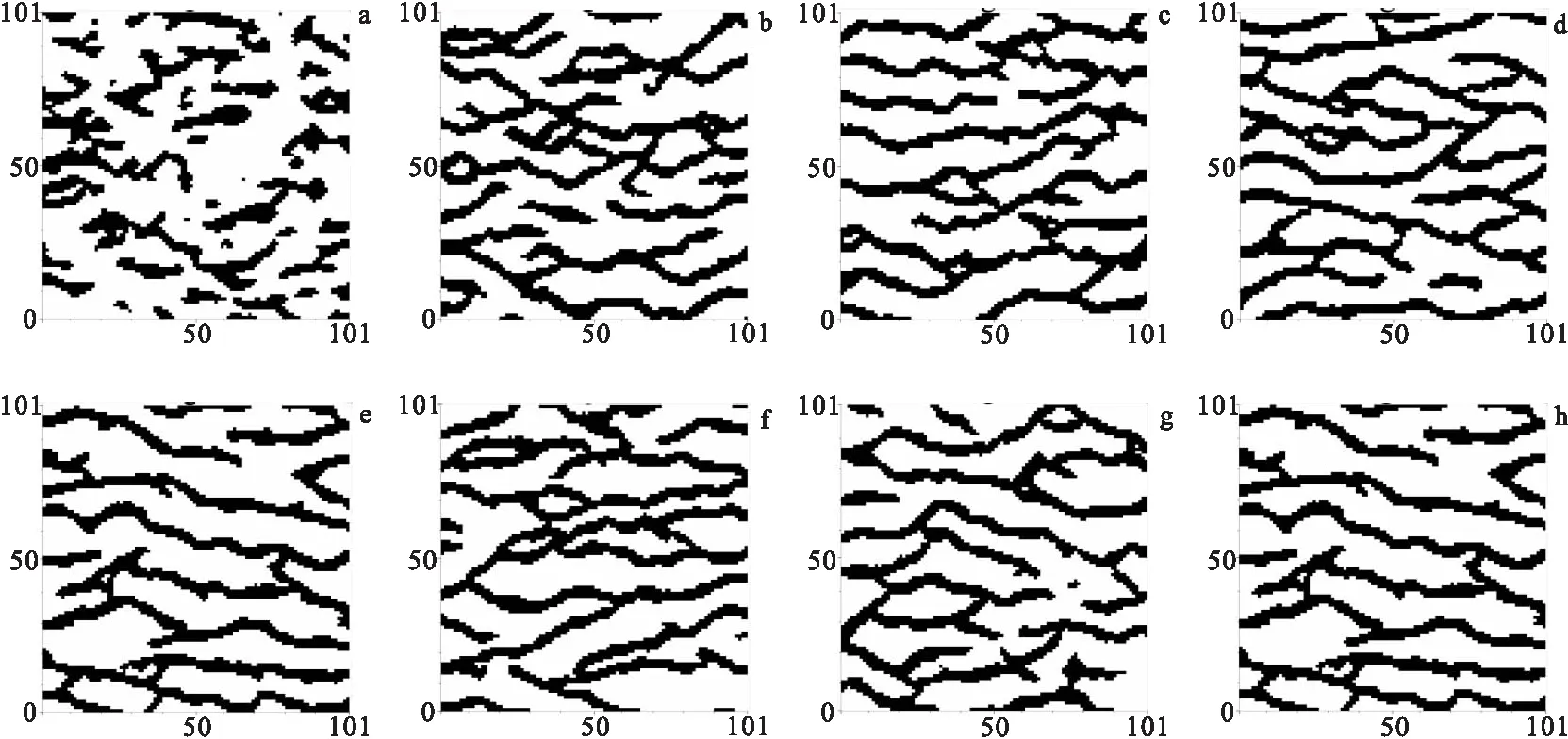
图8 不同网格重数对应的实现模型Fig.8 Implementation models corresponding to different multigrids(a)Multigrids=1;(b)Multigrids=2;(c)Multigrids=3;(d)Multigrids=4;(e)Multigrids=5;(f)Multigrids=6;(g)Multigrids=7;(h)Multigrids=8

利用余弦相似度cosSimilarity函数计算训练图像与随机模型连通性概率曲线的相似度，得到随机模型(多重网格重数1-8)与训练图像关于连通性概率的余弦相似度，然后取其相似度均值建立其对应多重网格重数变化的曲线(图 9)。

图9 建模参数(网格重数)基于连通性函数的余弦相似度变化曲线Fig.9 Cosine similarity change curve based on connectivity function for modeling parameters (multigrids)

随着多重网格数从1开始增加，300个随机模型与训练图像的相似度期望不断增加，表明模型与训练图像越来越相似(根据余弦相似度定义，余弦值越接近1，表示越相似)，当网格重数到3时，空间相关性评价指标进入一个平台区域，模型质量将不再有明显提升，参数敏感性降低。这是因为当网格很粗时，相应的用来扫描训练图像的样板规模会大于训练图像的规模，导致大的数据事件很难被找到。此时数据事件就会相应缩小，而这就等同于使用较小的数据样板进行扫描，一般来说，网格重数设置多少取决于最大尺度结构信息的大小，在本例中101×101的网格训练图像中，利用连通性方法定量化地给出最佳网格重数为3，超过3以后，模拟效果不会有明显改善，该实验结果也符合前人所提出的认识。

3 结论

采用基于连通性函数的多点地质统计学建模参数敏感性分析方法，分别对两个关键建模参数(搜索节点数、多重网格层数)进行敏感性测试，得出以下认识：

1)随着搜索节点数和多重网格层数增加，模型与训练图像的形态视觉特征越来越相似，利用连通性函数来量化这一空间相关性特征，结合余弦相似度度量方法对其进行定量的分析，找出价指标开始平稳、进入平台区域时的拐点所对应的参数值作为最佳参数。

2)针对本例101×101的河道训练图像，在snesim模拟过程中搜索节点数不能过少，过少捕捉不到河道的结构特征，过多并不能明显改善建模效果，参数在到达一定值后变得不敏感，反而会增加计算量，降低效率，多重网格层数也是如此。利用连通性的方法定量化的分析参数敏感性，找到搜索节点数设置在35左右，多重网格层数设置为3层，能获取良好模拟效果，也能减少不必要的运算，提高效率。