频散介质中的瞬变电磁响应特征和反演特性分析

智庆全， 武军杰， 王兴春， 杨 毅，张 杰，邓晓红

(1.中国地质科学院 地球物理地球化学勘查研究所，廊坊 065000;3.国家现代地质勘查工程技术研究中心，廊坊 065000;4.长安大学 地质工程与测绘学院，西安 710054)

0 引言

瞬变电磁法(TEM)因其体积效应小、分辨力高、对良导体敏感的优势，在金属矿产勘查、地质调查等领域得到了广泛的应用[1-3]。由于极化介质的广泛存在，大地固有频散特性，电磁场在地层中传播会产生频散效应，引起低频的激发极化(IP)效应和高频的介电极化[4]。在瞬变电磁法常见的工作条件下，介电极化效应较弱而难以体现，因而TEM响应中的频散效应一般为激发极化效应，其响应叠加在瞬变电磁响应之中。当地下存在极化地质体时，会产生较强的IP效应，导致瞬变电磁响应的畸变，破坏瞬变电磁响应随大地电性变化的正常衰减规律，甚至出现响应符号反转现象，给瞬变电磁数据处理带来了困难和干扰，以至于造成错误解释。研究和分析频散介质中的瞬变电磁响应特征及其反演特性，是瞬变电磁数据处理问题的关键和前提。

频散介质中瞬变电磁响应的畸变现象很早就引起了地球物理学者的注意，并引发了一系列有价值的讨论和分析。Spies[5]最先报道了澳大利亚矿产资源地质和地球物理局自1972年以来多次观测到的重叠回线装置的TEM响应符号反转现象，分析了造成这种现象的原因可能有磁性效应、电磁波的反射以及复电导率效应(包含位移电流和IP效应)等几种，并指出其中最为合理的解释是IP效应；Weidelt[6]从理论上证明，对于无频散介质中的重叠回线TEM响应，由于其积分核函数的严格非负性，任意的电导率和磁导率都不会导致其符号反转，从而确定了造成瞬变电磁响应符号反转的主要原因是频散介质的IP效应；Smith等[7]使用两个相互作用的阻抗环模拟了频散介质中瞬变电磁响应符号反转现象出现的过程，从物理上解释了频散介质中符号反转现象的产生机理。

在频散介质中瞬变电磁响应的定量分析方面，Pelton等[8]首先通过对大量岩矿石标本和露头的测量，证明了描述电极化的Cole-Cole模型同样适用于描述激发极化效应[9]，奠定了极化介质中瞬变电磁响应定量计算的理论基础；Lee[10]采用Cole-Cole模型推导了频散均匀半空间的瞬变电磁响应，利用级数展开给出了渐进表达式，证明了在频散地层中的IP效应会导致瞬变电磁响应的符号反转；Raiche[11-12]利用基于G-S变换的层状大地正演算法对Lee的结果进行了验证，取得了相一致的结果；Flis等[13]计算了含频散效应的一维地层和三维体瞬变电磁响应，系统分析了频散地层和频散体参数对TEM响应的影响，提出大地的频散效应可以分为充电和放电两个阶段，并尝试进行了含IP效应TEM数据的定量解释；殷长春等[14]利用积分方程法计算了两层大地中三维异常体的TEM响应，分析了影响三维极化体响应的因素；孙鸿雁[15]和王隆平等[16]分别通过理论分析和物理模拟研究了频散大地上极化体和观测参数对磁性源瞬变电磁响应的影响特征，讨论了通过指数函数拟合分离IP效应和增加发射磁矩、移动发射框位置等办法削弱IP效应的方法。Kozhevnikov等[17-22]和Antonov等[23]针对瞬变电磁中的IP效应开展了一系列研究，利用单纯形法对频散均匀半空间等简单模型的瞬变电磁法响应进行了反演，指出了频散地层中瞬变电磁响应的反演具有强烈的初始模型依赖，并讨论了通过联合反演和先验信息改进反演结果的方法；Yu等[24]利用SVD方法进行了频散地层中TEM响应的反演，提高了含IP效应的TEM数据的解释精度；顾建宁等[25]利用均匀半空间模型分析了TEM勘探中IP效应的影响规律，并根据反号现象直接确定了地下矿体的位置；Chen等[26]利用基函数拟合和符号约束进行了TEM响应和IP效应的分离，在弱频散地层上取得了良好的应用效果；陈帅等[27]通过Occam方法缓解了频散介质多参数引起的欠定性，实现了一维瞬变电磁Occam反演；Zhi等[28]为了解决频散介质中TEM数据反演的非单调问题，引入了粒子群算法进行了TEM数据反演目标函数的全局优化，进行了实测数据试算，较准确地恢复了频散地层的电阻率和极化率参数。

以上研究表明，当前关于频散效应对瞬变电磁响应的影响机理已经较为明确，在数据处理方面基本形成了响应曲线分析、频散响应和感应响应分离、考虑频散效应的多参数联合反演等三大类方法。其中多参数联合反演方法适用性最广且解释精度最高，但由于频散介质中瞬变电磁响应规律复杂、待求参数多，多参数联合反演方法具备较强的初始模型依赖。鉴于此，笔者将从频散介质中瞬变电磁响应特征、场随各参数变化的单调性和灵敏度、反演目标函数特性几个方面开展分析研究，探究反演方法中强初始模型依赖的原因，为进一步反演策略的合理构建提供理论支持。

1 正演方法

在进行频散介质瞬变电磁正演时，首先进行频率域电磁场正演，然后通过离散正弦变换得到时域电磁场响应。对于地层频散特性的模拟，通过Cole-Cole复电阻率模型实现。Cole-Cole模型可同时描述激发极化和介电极化效应，对于激发极化效应有：

(1)

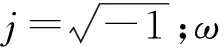
如图1所示建立一维大地模型和笛卡尔坐标系，第i层大地由其电性参数(σi，mi，ci，τi)和顶面Z坐标Zi唯一确定。采用时谐因子e-iωt，忽略位移电流，则电磁场控制方程可写为：

图1 一维大地模型Fig.1 The 1D layered-earth model

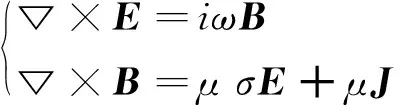
(2)

式中：μ为磁导率；ω为角频率；E和B分别代表电场强度和磁感应强度；J为电流密度矢量。引入库伦规范下的磁矢量势A：

B=▽×A

(3)

(4)

对于电偶极子和图1的一维模型，磁矢量势可通过汉克尔变换得到[29]：

(5)

瞬变电磁响应通过傅里叶变换得到，对于常见的TEM阶跃发射波形：

(6)

使用傅里叶变换对：

(7)

其中：F(ω)为频率域响应；f(t)为时间域响应。由于F(ω)实部和虚部的对称性，f(t)可以通过实数域的正弦变换获取。笔者采用精度较高、计算速度较快的双精度160点数字滤波器进行正弦变换，并通过电偶极子叠加技术求取任意形状发射回线的瞬变电磁响应[30]。

Lee[10]给出了频散大地上瞬变电磁响应的渐近表达式，并基于Lornex、Copper cities侵染状硫化物铜矿和Kidd Creek块状硫化物矿床的地电参数进行了正演计算。为验证本文算法的正确性，将计算结果与Lee的结果进行了对比。所采用的计算参数为：重叠回线装置，发射线框半径为25 m，观测z分量衰减电压ε，发射电流为1 A，地电模型参数见表1。三个地电模型的对比验证结果如图2所示，计算结果和Lee的渐近解析解基本吻合，响应曲线的均方相对误差分别为3.52%、2.76%和5.95%，证明了算法的准确性。衰减曲线在1 ms左右出现的转折代表瞬变电磁响应发生了符号反转，说明此时频散效应的放电电流强度超过了感生涡流，且方向与感生涡流相反，符号反转后的观测电压主要是频散效应引起的。

表1 验证模型地电参数Tab.1 Geoelectrical parameters of verification models

图2 正演结果验证Fig.2 Validation of the modeling results(a)Lornex模型;(b)Copper cities模型;(c)Kidd Creek模型

2 频散介质中瞬变电磁响应特征

基于Lee和Pelton对频散现象的研究，采用实际工作中常遇到的观测参数，设计典型均匀半空间模型，其地电参数如表2所示。以此为基础，分别改变电阻率、充电率、时间常数、频率相关系数，研究频散介质中的瞬变电磁响应特征。发射装置采用边长为100 m的中心回线，发射电流为15 A，观测衰减电压z分量。图3(a)～图3(d)分别为不同电阻率、充电率、频率相关系数、时间常数均匀半空间的TEM响应曲线。

表2 设计均匀半空间模型的地电参数Tab.2 Geoelectrical parameters of designed half-space model

从图3(a)可以看出，地层电阻率越高，TEM曲线符号反转现象出现越早。当电阻率低到一定程度时，观测时间范围内不出现符号反转现象。这是由于电阻率越高，感应TEM场衰减越快，频散效应能够在较早的时间上得以显现。从图3(b)可以看出，充电率越高，符号反转现象出现越早。这是因为充电率越高，频散介质储存能量越大，充放电过程的频散效应越强。从图3(c)可以看出，场关于频率相关系数的变化特征较为复杂。在频率相关系数较小时，随频率相关系数增大，符号反转现象的出现时间逐渐提前；而频率相关系数大于一定值之后，符号反转现象出现时间则又逐渐变晚。从图3(d)可以看出，在时间常数很小时，观测时段内未出现符号反转现象；随时间常数增大，反号现象再次出现且时间逐渐提前，频散效应增强；当时间常数大于一定值之后，反号现象出现时刻逐渐变晚，频散响应减小。当时间常数很大时，在观测时间范围内不出现反号现象。不同地电参数的TEM响应曲线发生了多次交叉，表明频散介质中的TEM响应随地电参数的变化具有较强的非单调性。

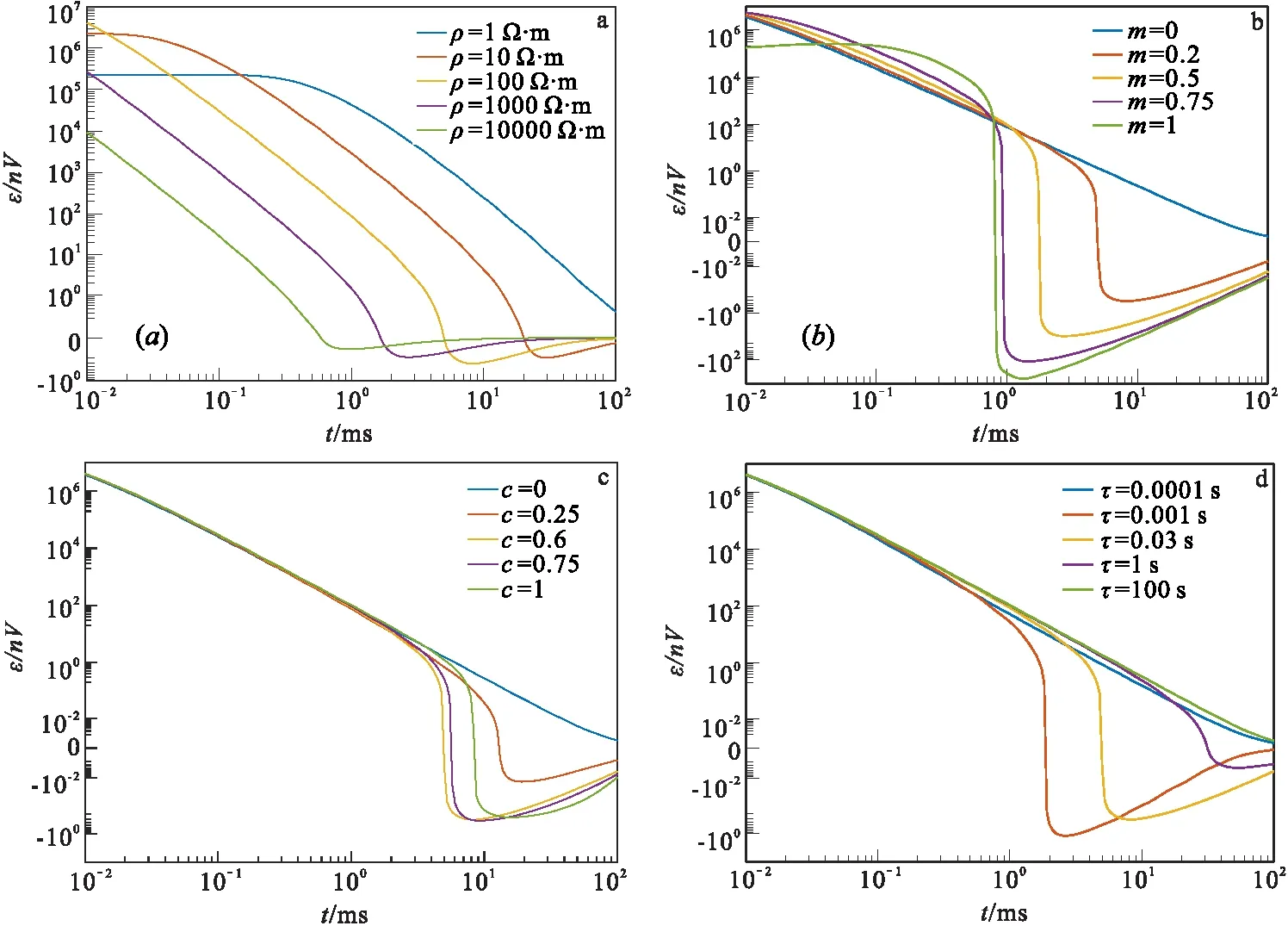
图3 不同参数均匀半空间的TEM响应曲线图Fig.3 TEM response curves of uniform half space with different parameters(a)不同电阻率；(b)不同充电率；(c)不同频率相关系数；(d)不同时间常数

图4为不同发射边长情况下均匀半空间的TEM响应曲线。由图4可以看出，发射边长越大，符号反转现象出现越晚，频散效应幅值越小。当发射边长增大到一定程度时，观测时间范围内不出现符号反转现象。这是由于随发射边长增加，有效发射磁矩以二次方增加，感应瞬变电磁场强度显著增强，导致频散效应被较强的感应场所掩盖，仅当感应场衰减到较晚期、幅度大幅减小时才能有所体现。

图4 均匀半空间不同发射边长时的TEM响应曲线图Fig.4 TEM response curves of uniform half space with different length of transmitting loop

3 瞬变电磁响应函数的单调性特征

为研究频散介质中瞬变电磁响应随地电参数变化函数的单调性特征，仍使用前面设计的均匀半空间模型和观测参数，分别将电阻率、充电率、时间常数、频率相关系数作为变量进行正演模拟，结果如图5～图8所示。

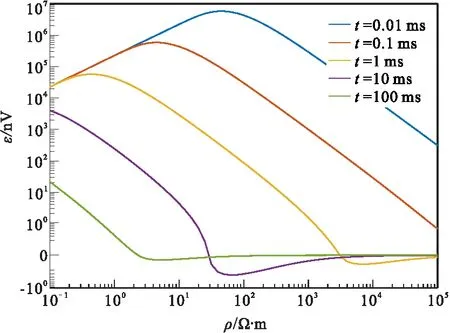
图5 随电阻率变化的TEM响应函数图Fig.5 TEM response function of resistivity

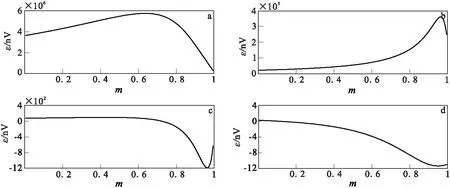
图6 随充电率变化的TEM响应函数图Fig.6 TEM response function of chargeability(a)t=10-5s;(b)t=10-4s;(c)t=10-3s;(d)t=10-2s

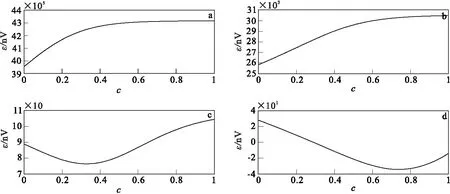
图7 随频率相关系数变化的TEM响应函数图Fig.7 TEM response function of frequency dependence(a)t=10-5s;(b)t=10-4s;(c)t=10-3s;(d)t=10-2s

图8 随时间常数变化的TEM响应函数Fig.8 TEM response function of time constant(a)t=10-5s;(b)t=10-4s;(c)t=10-3s;(d)t=10-2s

图5为电阻率在10-1Ω·m ～105Ω·m范围变化时不同时刻的TEM衰减电压函数曲线，可以看出当存在频散效应时，TEM衰减电压相对于电阻率的函数为连续、可导、非单调函数。相比于无频散大地的情况，其非单调特征更为复杂，其响应函数包含负值，且至少包含1个极大值点和1个极小值点。

图6和图7分别为充电率m和频率相关系数c在其定义域[0, 1]范围内变化时，对应不同观测时刻的TEM响应。由于不同时刻TEM衰减电压值具有较大的量级差异，为便于观察分析，将对应观测时刻t=10-5s、t=10-4s、t=10-3s、t=10-2s的函数曲线分别绘制为图6和图7。从图6与图7中可以看出，对于有频散效应的均匀半空间，其瞬变电磁响应函数均为非单调函数，至少包含1个极值点。

图8为时间常数τ在10-8s～105s范围变化时，对应不同观测时刻的TEM衰减电压函数曲线，此时TEM响应函数仍为至少包含1个极值点的非单调函数。值得注意的是，当时间常数τ值增大或减小到一定程度后，TEM响应趋于一个定值，对τ值的变化几乎没有反映，说明此时瞬变电磁响应对大地介质时间常数的变化“不敏感”。同时随着观测时刻增大，瞬变电磁响应随时间常数变化较大的“敏感段”逐渐后移，表明瞬变电磁晚期响应对于具有较大时间常数的频散效应敏感，而早期响应对于较小时间常数的快速频散效应敏感。

4 瞬变电磁场对地电参数的灵敏度

灵敏度是反问题求解中的重要参数，用以表征参数对观测响应或数据的影响程度。为进一步分析频散介质中瞬变电磁响应对不同地电参数的敏感性，需计算分析各地电参数的灵敏度。由于不同地电参数的量纲不同，其灵敏度矩阵也具有不同的量纲。为便于对比，将灵敏度利用响应值进行归一处理，以衰减电压为例，归一灵敏度表示为式(8)。

(8)

其中：p分别代表电阻率ρ、充电率m、频率相关系数c、时间常数τ四个地电参数。其意义为当地电参数p变化1倍时，TEM响应变化的倍数。

归一灵敏度作为场对地电参数的导数，其变化特征较为复杂，不适合通过函数图像呈现。使用上面设计的均匀半空间模型，将对应不同观测时刻的各参数灵敏度数据列在表3中。

由表3的灵敏度数据可以看出，电阻率参数的灵敏度幅度在观测时窗范围内差异不大，总体变化范围约为1个量级，并在5 ms时刻附近达极大值；充电率参数的灵敏度特征与电阻率参数类似，但在5 ms时刻附近达到的幅度极大值远大于其它时刻；频率相关系数和时间常数的灵敏度幅值在不同时刻的变化较大，观测视窗内变化范围达3个量级以上，在早期灵敏度幅度较小，随时间推移迅速增加并在5 ms时刻附近达极大值，随后缓慢降低。各地电参数的灵敏度变化规律表明，瞬变电磁响应在全时段上均受地下电阻率和充电率的控制，具有较高的灵敏度值和良好的幅度变化规律；瞬变电磁响应对于频率相关系数和时间常数具有相对“窄带”的灵敏度，即仅在与大地时间常数相当的观测时窗范围内具备相对较高的灵敏度，而在偏离该时窗范围的较早期和晚期，灵敏度较低。

5 频散介质中TEM响应反演特性

前人关于频散介质中瞬变电磁响应的反演研究表明，考虑频散效应的联合反演技术具有很强的多解性，反演结果严重依赖于初始模型[18]。为分析此现象产生的原因，笔者采用目前联合反演中常用的目标函数展开计算模拟，分析反演目标函数的特性。针对联合反演中的多解性问题，探讨可能的解决方法和途径。

数据的反演实际上是一个将目标函数最小化的过程，从最佳地拟合观测数据和压制干扰的角度出发，一般选取最小二乘目标函数[22, 27-28]，其一般形式为式(9)。

(9)

其中：d为TEM响应数据；Cm为数据方差矩阵。

分别取电阻率、充电率、频率相关系数、时间常数的其中两个参数作为自变量，计算目标函数值并绘制函数图像。图9、图10和图11分别展示了目标函数关于地电参数(ρ，τ)、(ρ，m)、和(ρ，c)变化的三维图像，可以看出，即使在均匀半空间条件下，目标函数关于地电参数的变化也是非单调的，且响应规律较为复杂，其函数图像呈梯田状，包含有大量的局部极小；全局极小值唯一，邻域内目标函数变化梯度较大，全局极小点附近函数图形变化尖锐；远离全局极小的目标函数梯度迅速减小，函数图形趋于平坦。根据目标函数特征容易判断，正是由于大量局部极小点的存在，造成了传统反演方法具有强多解性和强初始模型依赖的现象，考虑频散效应的瞬变电磁响应反演难以通过线性最优化方法实现。全局最优算法可有效地解决局部极小问题，但过度平坦的目标函数会使得全局优化算法难以找到正确的修正方向而难以收敛。因此，还需考虑对目标函数加以改造，对偏离全局极小的目标函数值增加惩罚项，或通过参数约束限制寻优范围，以保证全局寻优算法的收敛性。

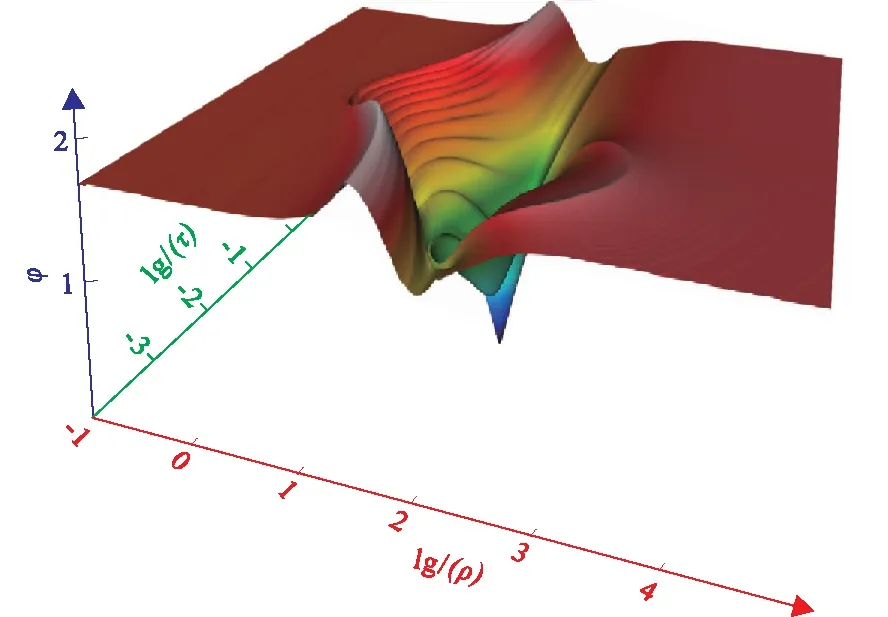
图9 目标函数随电阻率和时间常数的变化Fig.9 Objective function varies with resistivity and time constant

图10 目标函数随电阻率和充电率的变化Fig.10 Objective function varies with resistivity and chargeability

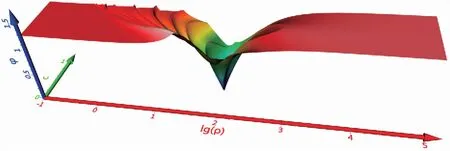
图11 目标函数随电阻率和频率相关系数的变化Fig.11 Objective function varies with resistivity and frequency dependence

6 结论

频散介质中的瞬变电磁响应是地层中电磁感应效应和频散效应相互耦合的综合效应，响应规律较为复杂。笔者以一维层状大地为例，应用Cole-Cole模型和时频转换技术，实现了频散介质中瞬变电磁响应的正演模拟。结合前人研究和实际工作的常见参数设计了典型地电模型，研究频散介质中瞬变电磁场的响应规律及单调性、灵敏度特征；根据联合反演工作中常用的目标函数，探讨频散介质中瞬变电磁响应的反演特性。主要得出以下认识和结论：

1)基于Cole-Cole模型和数字滤波技术的频散介质TEM正演方法与Lee所给出的渐近解析解基本吻合，验证了本文算法的正确性。

2)瞬变电磁响应的符号反转现象代表频散效应的强度超过了感生涡流场，其产生时刻与大地电阻率、充电率和发射边长的关系具有较简单的相关性，与频率相关系数和时间常数的关系较为复杂。

3)频散介质中瞬变电磁响应随地电参数变化的函数具有连续、可导、非单调特征，不存在简单的线性关系。

4)瞬变电磁场对大地电阻率和充电率的灵敏度较高且幅度特性良好，对于频率相关系数和时间常数具有“窄带”特征，即仅在与大地时间常数相当的观测时窗范围内，具备相对较高的灵敏度。

5)频散介质中瞬变电磁场反演目标函数具有大量的局部极小点，是造成传统联合反演存在多解性和强初始模型依赖的主要原因。采用全局最优算法可能解决局部极小问题，但需考虑通过引入惩罚项或参数约束等手段提高全局最优算法的收敛性。