ECC2-131 的并行Pollard rho 算法实现分析*

关沛冬, 罗玉琴, 张方国, 田海博

1. 中山大学计算机学院, 广州 510006

2. 广东省信息安全技术重点实验室, 广州 510006

1 引言

有限域上基于椭圆曲线的公钥密码学是1985 年由Koblitz[1]和Miller[2]提出的. 从那时起, 有限域上的椭圆曲线被应用在许多密码系统和密码协议中, 如Diffie-Hellman 密钥协议方案[3]、椭圆曲线数字签名算法[4]等. 椭圆曲线密码体制的安全性是基于椭圆曲线离散对数问题(ECDLP) 这一困难问题. 解决ECDLP 意味着破解了ECC, 因此这一困难问题受到了各界的广泛关注.

1997 年, Certicom[5]提出了ECC 挑战, 其本质是求解ECDLP. 有限域大小小于100 位的挑战被当作练习被快速解决, 有限域大小大于100 位的挑战则分为两种级别. 第一级是109 位和131 位的挑战; 第二级是163 位、191 位、239 位和359 位的挑战. 迄今为止, ECC2K-108、ECC2-109、ECCp-109 已经被解决. Bailey 等人[6]曾通过网上大量征集计算资源尝试攻击ECC2K-130, 但是最后没有给出成功攻击的结果. ECC2-131 等更困难的挑战则迄今没有被解决.

Pollard[7]在1978 年基于生日攻击提出了一种求解一般循环群离散对数的算法, 这种算法被称为rho 算法. 设G是一个循环群, 则Pollard rho 算法的迭代函数是一个函数F:G →G, 而且此函数从一个初始点P0出发, 依次产生Pi+1=F(Pi), 其中i= 0,1,···. 其中通过映射函数产生的元素序列为P0,P1,···. 由于Pi ∈G, 而循环群的阶|G| 是有限的, 因此该序列一定会产生一个元素与前面的某个元素相同. 这种现象称为碰撞或者匹配. 当碰撞产生后, 将有很大概率求解出离散对数问题的解.

对于求解ECDLP, 由Gallant 等人[8]和Wiener 等人[9]所修改的两种Pollard rho 算法是迄今最有效的通用求解算法. Van Oorschot 等人[10]提出了一种并行化的Pollard rho 算法, 这种算法通过并行计算的方法能线性提高求解离散对数问题的效率, 而且适用于现代计算机的计算结构, 能高效地用程序实现. 分布式Pollard rho 算法是目前大家公认的最有效的解决一般循环群离散对数的算法.

自从分布式Pollard rho 算法提出以来, 多位密码学家在该基础上提出了各种优化算法和改进方案.而这些工作都主要都是对Pollard rho 算法的迭代函数进行优化. Teske[11]通过在迭代函数中使用更多的点加运算, 提出了高效的r-加游走迭代函数. Teske 还提出并分析了r+q-混合游走迭代函数, 他在r-加游走迭代函数中引入了倍点运算. 然而,r+q-混合游走会降低一定的随机性, 并且在椭圆曲线的仿射坐标下, 倍点运算的效率不比点加运算的效率高. Bessalov[12]首先在ECDLP 中使用了半分的思想, 但是他没有对该算法进行详细分析. Zhang 和Wang[13]使用椭圆曲线点半分运算为Pollard rho 算法提出了一个新的迭代函数r+h-混合游走, 但是在分析的过程中没有考虑椭圆曲线点加运算的高效实现对他们所提算法的影响.

本文针对ECC2-131, 对基于r-加游走,r+q-混合游走和r+h-混合游走这三种不同迭代函数的分布式Pollard rho 算法进行快速实现, 并对其算法性能进行比较, 发现迭代函数为r-加游走的分布式Pollard rho 算法在理论与程序实现上具有优势. 本文还给出了基于ECC2-131 对三种分布式Pollard rho 算法的软件实现, 以及给出了针对有限域F2131的最优不可约多项式. 使用该不可约多项式进行编程实现能对有限域F2131模运算的运算效率提高11.29%, 对乘法运算的运算效率提高11.23%. 最后本文给出了基于r-加游走的分布式Pollard rho 算法在工作站和在天河二号超级计算机中运行的效率, 发现在超级计算机中需要消耗约1296.41×106核时, 花费约1.296 亿元才能攻破ECC2-131. 由此可见当前ECC2-131 仍然是个无法有效解决的问题.

2 预备知识

2.1 椭圆曲线以及椭圆曲线离散对数问题(ECDLP)

令Fq是有q个元素的有限域, 定义在有限域Fq上的椭圆曲线E是由一个非奇异的Weierstrass 方程所定义的. 该非奇异Weierstrass 方程为:

设E是一条定义在有限域上的椭圆曲线. 设点P是一个阶为n的点. 定义群G是由点P生成的n阶循环群. 对于任意的Q ∈G, 存在整数s,0≤s ＜n, 使得Q=sP成立, 其中sP表示s个点P相加.因此, 给定椭圆曲线E以及其中满足Q=sP的点P,Q, 求出整数s就是椭圆曲线离散对数问题, 简称ECDLP.

2.2 椭圆曲线离散对数求解方案

Pollard rho 算法的工作原理是,首先定义一个周期性循环的元素序列,然后在序列中寻找两个“碰撞”的元素. 而分布式Pollard rho 算法则是在Pollard rho 算法的基础上筛选一些具有某些性质的可区分元素, 然后只在这些可区分元素上面去寻“碰撞”. 分布式Pollard rho 算法的两个关键思想是生成序列化的迭代函数和“碰撞” 检测算法. 本节将介绍分布式Pollard rho 算法以及三个比较具有代表性的迭代函数.

若gcd(bi-bj,n)=1, 则s=(aj-ai)(bi-bj)-1modn, 从而求解出ECDLP.

Pollard rho 算法在迭代的过程中迭代函数会产生大量的点. 为了减少迭代点的存储, 只存储可区分点是一种常见的手法, 存储过程中通过筛选满足一定条件的点, 能减少大量迭代点的存储. 定义群G中的一个子集D, 其中D包含了所有的满足特殊条件的点的集合, 例如具有固定数量的前导零的元素. 集合D中的点被称为可区分点. 分布式Pollard rho 算法的核心思想在于多个程序同时执行迭代函数, 实现快速大量的随机游走以加速碰撞的发生.

接下来将会介绍在Pollard rho 算法的三种改进的迭代函数, 分别是Teske[14]提出的r-加游走和r+q-混合游走, 还有Zhang[13]等人提出的r+h-混合游走.

2.2.2r-加游走迭代函数

根据Teske[14]提出的r-加游走(r-adding walk) 迭代函数, 随机选取2 个整数序列, 每个序列有r个整数:

2.2.4r+h-混合游走迭代函数

根据Zhang[13]等人提出的r+h-混合游走(r+h-mixed walk) 迭代函数, 随机选取2 个整数序列,每个序列有r个整数:

3 有限域F2131 的实现与改进

ECC2-131 是Certicom[5]公司设立的椭圆曲线离散对数的挑战, 直至目前该挑战还没有被攻破. 本文将根据此挑战设计出最优的程序实现方案.

3.1 有限域F2131 基本运算的实现

ECC2-131 的详细参数见文献[16], 它所在的有限域F2131的不可约多项式为f(z) =z131+z13+z2+z+1.为了令分布式Pollard rho 算法在求解ECC2-131 的过程中达到最高效率,实现分布式Pollard rho 算法的程序使用SIMD 指令对有限域F2131的基本运算进行优化. 在有限域元素数据结构的设计上,每个元素由2 个128 位的整数组成. 若e ∈F2131, 把e写成多项式的形式

记为(e130,e129,··· ,e0). 因此使用一个128 位整数存储(e127,e126,··· ,e0), 使用另一个128 位整数存储(0,··· ,0,e130,e129,e128), 其中e130前有125 个0.

有限域F2131的快速模运算参考文献[17] 中所使用的算法, 实现模运算的时候把有限域的元素使用多个64 位的整数表示. 与此同时, 模运算仅是乘法运算的一个部分, 因此要执行模运算的多项式的最高次幂不大于260. 因此最多只需要5 个64 位的整数即可表示要执行模运算的多项式, 记为e=(E[4],E[3],E[2],E[1],E[0]). 模运算运行的结果则使用3 个64 位整数表示. 在程序实现过程中, 将两个64 位的整数封装成一个128 位的整数, 然后使用Intel SSE 指令进行移位、异或等操作, 使程序具有更高的运行效率. 具体的模运算算法见算法1.

算法1 F2131 模运算Input: e = (E[4],E[3],E[2],E[1],E[0]).Output: b = e mod f(z).1 for i = 4 →3 do 2T ←E[i];3E[i-3] ←E[i-3]⊕(T ≪61)⊕(T ≪62)⊕(T ≪63);4E[i-2] ←E[i-2]⊕(T ≪10)⊕(T ≫1)⊕(T ≫2)⊕(T ≫3);5E[i-1] ←E[i-1]⊕(T ≫54);6 end 7 T ←(E[2]&0xFFFFFFFFFFFFFFFC);8 B[0] ←E[0]⊕(T ≪10)⊕(T ≫1)⊕(T ≫2)⊕(T ≫3);9 B[1] ←E[1]⊕(T ≫54);10 B[2] ←E[2]&0x7;11 return b ←(B[2],B[1],B[0]);

有限域F2131的快速乘法运算可以通过Karatsuba 算法[15]减少多项式相乘时所需要执行的乘法次数. 在编程实现上, 通过使用大部分CPU 都支持的PCLMULQDQ 指令[18], 可以在几个CPU 周期内完成64 位特征为2 的有限域的乘法运算. 具体乘法运算如算法2 所示.

算法2 F2131 乘法Input: a = (A[2],A[1],A[0]),b = (B[2],B[1],B[0]).Output: c = ab.1 T0 ←A[1]⊕A[2];2 T1 ←B[1]⊕B[2];3 T2 ←A[0]⊕A[2];4 T3 ←B[0]⊕B[2];5 T4 ←A[0]⊕A[1];6 T5 ←B[0]⊕B[1];7 T0 ←PCLMULQDQ(T 0,T 1);8 T1 ←PCLMULQDQ(T 2,T 3);9 T2 ←PCLMULQDQ(T 4,T 5);10 T3 ←PCLMULQDQ(A[0],B[0]);11 T4 ←PCLMULQDQ(A[1],B[1]);12 T5 ←PCLMULQDQ(A[2],B[2]);13 T6 ←T0 ⊕T4 ⊕T5;14 T7 ←T2 ⊕T4 ⊕T3;15 T8 ←T1 ⊕T3 ⊕T4 ⊕T5;16 c ←(T5,T6,T8,T7,T3);17 return c;

算法3 F2131 开平方根Input: e = (e130,e129,··· ,e0).Output: c = ■e.1 eodd ←(e129,e127,··· ,e1);2 eeven ←(e130,e128,··· ,e0);3 c ←■z ×eodd mod f(z);4 c ←c ⊕eeven;5 return c;

有限域F2131的解一元二次方程的具体算法在文献[19] 中被详细地描述. 具体解一元二次方程组如算法4 所示. 令Tr(e) 表示有限域元素的迹(trace), 其中e ∈F2m. 则

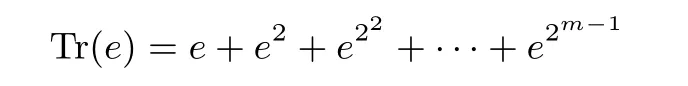
令H(e) 表示有限域元素的半迹(half-trace), 其中e ∈F2m. 则迹与半迹的计算方法在文献[19] 中有详细的介绍.

算法4 F2131 解一元二次方程Input: e = (e130,e129,··· ,e0).Output: z2 +z = e+Tr(e) 的解c, 其中z 为变量.1 预计算: ∀i ∈{1,2,··· ,65}, 计算H(z2i-1);2 c ←0;3 for i = 65 →1 do 5 e ←e ⊕zi;4if e2i = 1 then c ←c ⊕zi;7end 8 end 9 c ←c ⊕∑65 i=1 e2i-1H(z2i-1);6 10 return c;

常见的有限域F2131上的求逆算法有基于欧几里得算法的扩展欧几里得算法和基于费马小定理的Itoh-Tsujii 求逆算法[20]. 虽然广义欧几里得算法的平均复杂度比Itoh-Tsujii 求逆算法的复杂度要低, 但是通过大量的实验发现Itoh-Tsujii 求逆算法的性能更加稳定, 其平均开销会比广义欧几里得算法的要少.因此本文使用Itoh-Tsujii 求逆算法实现有限域F2131求逆运算.

3.2 有限域F2131 上最优不可约多项式

文献[17] 中给出了有限域F2131的快速模运算算法, 算法1 把有限域求模运算分为两个部分. 算法的输入是260 位的一个整数. 算法的第一部分把192 到260 位的数通过(2) 式的关系移位到低位, 并与低位的数进行异或; 算法第二部分把131 到191 位的数移位到低位并异或. 有限域上的不可约多项式为f(z)=z131+z13+z2+z+1, 则有

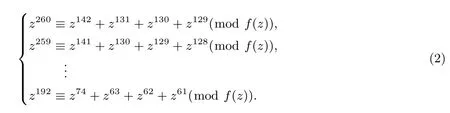
第一部分的运算会把[192,260] 位的数移位异或到[61,142] 位中, 由(2) 式可知算法的第一部分可分为3 次移位异或运算. 第一次运算把需要异或到[61,63] 位的数进行移位异或; 第二次运算把需要异或到[64,127] 位的数进行移位异或; 第三次运算把需要异或到[127,142] 位的数进行移位异或.

当不可约多项式有z3这一项的时候, 192 到260 位的数会与64 到132 位进行异或. 此时模运算的第一部分没有第一次运算; 第二次运算将会把192 位到255 位的数异或到64 到127 位中; 第三次运算把256 到260 位中的数异或到128 到132 位中.

本文找出在此模运算下运行效率最高的其中一个最优不可约多项式:f(z)=z131+z8+z3+z2+1,并编程实现了其模运算.只要选取包含单项的幂次为3 而且除了z131的单项其它单项的幂次不要超过54 的不可约多项式, 那么该不可约多项式即为最优不可约多项式. 不可约多项式f(z)=z131+z8+z3+z2+1的模运算的运算时间与ECC2-131 的不可约多项式的模运算的运算时间如表1 所示. 测试环境为: Intel Core i7-7940X CPU @ 3.10 GHz; Ubuntu 18.04 操作系统. 本文对乘法运算和模运算进行50 次测试, 每次测试测量200 000 次模运算和乘法运算所使用的CPU 周期, 并去除大于最小值10% 的数据取平均, 从而得到模运算和乘法运算的运算效率.

表1 F2131 上非最优不可约多项式与最优不可约多项式执行200 000 次模运算和乘法运算平均需要的CPU 周期Table 1 Average CPU cycles required to perform 200 000 modular and multiplicative operations between non-optimal irreducible polynomials and optimal irreducible polynomials on F2131

对于ECC2-131, 通过Zierler[21]等人的方法找出不可约多项式为f(z)=z131+z8+z3+z2+1 的有限域与ECC2-131 中的有限域的同构映射, 可以诱导出ECC2-131 所使用的椭圆曲线在新的有限域中的同构映射, 从而找出椭圆曲线加法群的同构映射. ECC2-131 中的椭圆曲线加法群的离散对数问题与同构映射后的加法群的离散对数问题是一致的, 因此本文在实现分布式Pollard rho 算法时使用了这种同构映射的方法实现求解ECC2-131 的加速.

4 重新认识基于不同迭代函数的分布式Pollard rho 算法的效率

本节将会对3 种基于不同迭代函数的分布式Pollard rho 算法的效率进行分析.

分布式Pollard rho 算法的迭代函数主要涉及椭圆曲线上的三个运算, 分别是点加、倍点和半分运算.其中涉及到的有限域上运算为加法、乘法、求逆、平方、开平方根和解二次方程. 使用多项式基表示的有限域F2m中的元素的加法运算在编程实现上仅需要少数异或指令, 远小于乘法运算的开销. 因此在加法运算与乘法运算数量差不多的情况下, 可以选择性地忽略加法运算的开销. 设乘法运算的开销为M, 求逆运算的开销为I, 平方运算的开销为S, 开平方根运算的开销为Sqr, 解二次方程的运算为Sol. 本文把乘法运算的时间作为基准, 然后测量出有限域上求逆、平方、开平方根和解二次方程这四种运算与乘法运算的时间比例, 从而在分析三种分布式Pollard rho 算法效率时只用乘法运算的开销表示. 记:

其中i,s,sqr,sol∈R.

4.1 分布式Pollard rho 算法的具体实现

基于迭代函数为r-加游走、r+q-混合游走与r+h-混合游走的分布式Pollard rho 算法只是迭代函数不相同, 其初始化过程都是相同的. 分布式Pollard rho 算法具体流程如下.

已知点P,Q满足P=sQ. 点P生成的群G的阶为n. 首先随机生成2r个正整数mi,ni ∈{1,2,··· ,n-1}, 计算出r个点Mi. 接下来随机生成2 个序列, 每个序列中有256 个元素, 这两个序列记为(a0,a1,··· ,a255),(b0,b1,··· ,b255), 其中ai,bi ∈{1,2,··· ,n-1},i=0,1,··· ,255. 用这两个序列计算出256 个椭圆曲线E上的点Pi=aiP+biQ. 令这256 个点作为初始点, 然后执行迭代函数, 直到碰撞发生. 迭代函数每生成一个可区分点, 则判断是否有碰撞发生.

4.2 r-加游走迭代函数实现

r-加游走迭代函数计算迭代点Pi需要使用椭圆曲线的点加运算.r-加游走迭代函数还需要计算满足Pi=aiP+biQ的两个整数ai,bi.椭圆曲线的点加运算需要用到1 个求逆、2 个乘法、1 个平方运算.通过使用Montgomery trick[22]的方法计算求逆运算可以快速求出N个有限域元素的逆, 把原本需要NI的计算开销转换为1I+(3N-3)M的计算开销. 本文把快速求出N个有限域元素的逆Montgomery trick的方法称为同时逆算法. 实现r-加游走迭代函数的程序中, 定义了N=256 个起始点, 迭代函数的每一次循环对这N个点分别进行一次迭代. 之所以要这样设计, 是因为点加运算中每个点都需要进行一次求逆运算, 而且在仿射坐标下求逆运算的计算开销远大于乘法运算的计算开销. 通过同时逆的方法能对求逆运算的运算效率有大幅度的提升. 通过这种设计, 迭代函数每一次循环就生成了N个迭代点. 具体r-加游走迭代函数的伪代码如算法5 所示:

算法5 r-加游走迭代函数Input: N = 256; N 个初始点Pi,i ∈{0,1,··· ,N -1}; 常数r; r 个点Mj,j ∈{0,1,··· ,r-1}.Output: ai,bi,aj,bj 满足Pi = aiP +biQ,Pj = ajP +bjQ, 其中Pi = Pj,i ／= j.1 for i = 0 →(N -1) do 2vi ←Pi.x mod r;3si ←Mvi.x+Pi.x;4 end 5 同时逆算法求出s-1 i ,i = 0,1,··· ,N -1;6 for i = 0 →(N -1) do 7利用s-1 i 计算Pi = Pi +Mvi;8ai ←ai +mvi;9bi ←bi +nvi;10if Hamming(Pi.x) ＜= 28 then 11DList.append(Pi,ai,bi) ;12判断DList 中是否有(Pj,aj,bj) 满足Pi = Pj 且i ／= j, 若满足, return ai,bi,aj,bj;13end 14 end 15 goto 1

算法5 中ai,bi的计算为两个数相加然后模n, 因为ai,bi ＜n, 所以ai+bi ＜2n. 因此模运算可以简化为整数减法运算. 则计算ai,bi最多需要2 个整数加法运算、2 个判断和2 个整数减法运算, 其计算量仍然小于有限域上的乘法运算的计算量. 由上述分析以及迭代算法伪代码可得,r-加游走迭代函数平均每个迭代点的计算开销为:

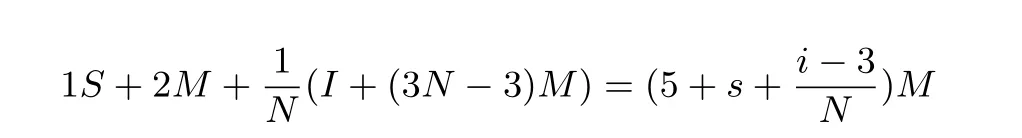
4.3 r+q-混合游走迭代函数实现

r+q-混合游走迭代函数使用椭圆曲线中的点加和倍点运算. 由4.2 节可知点加运算的计算开销为2M+ 1S+ 1I. 椭圆曲线的倍点运算需要用到1 个求逆、2 个乘法、2 个平方运算, 因此其计算开销为2M+2S+1I. 与此同时, 倍点运算与点加运算都需要用到求逆运算, 因此同样可以使用同时逆的方法进行优化, 即把求逆运算的NI的开销转换为I+(3N-3)M. 在实现r+q-混合游走迭代函数的程序中迭代函数的每一次循环对N个点分别进行一次迭代. 此迭代函数与r-加游走迭代函数的区别在于计算完同时逆后, 需要使用判断语句判断当前迭代点执行的是倍点还是点加运算. 具体r+q-混合游走迭代函数的伪代码如算法6 所示:

算法6 r+q-混合游走迭代函数Input: N = 256; N 个初始点Pi,i ∈{0,1,··· ,N -1}; 常数r; r 个点Mj,j ∈{0,1,··· ,r-1}; 常数q.Output: ai,bi,aj,bj 满足Pi = aiP +biQ,Pj = ajP +bjQ, 其中Pi = Pj,i ／= j.1 for i = 0 →(N -1) do 2vi ←Pi.x mod (r+q);3si ←Mvi.x+Pi.x;4 end 5 同时逆算法求出s-1 i ,i = 0,1,··· ,N -1;6 for i = 0 →(N -1) do 7if vi ＞= r then 8利用s-1 i 计算Pi = 2Pi;ai = 2ai mod n;10bi = 2bi mod n;11else 9 12利用s-1 i 计算Pi = Pi +Mvi;13ai ←ai +mvi;14bi ←bi +nvi;15end 16if Hamming(Pi.x) ＜= 28 then 17DList.append(Pi,ai,bi) ;18判断DList 中是否有(Pj,aj,bj) 满足Pi = Pj 且i ／= j, 若满足, return ai,bi,aj,bj;19end 20 end 21 goto 1

根据文献[11], Teske 对自身提出的r+q-混合游走与r-加游走进行了详细的性能分析. 在r+q-混合游走迭代函数中,r与q的取值以及两者的比值不同对算法的随机性与计算效率都有影响. 对于r+q-混合游走迭代函数, 需要考虑r,q的取值的对r+q-混合游走算法平均每个迭代点的计算开销的影响, 并忽略有限域加法运算以及计算ai,bi所带来的计算开销. 由上述分析以及迭代算法伪代码可得,r+q-混合游走迭代函数平均每个迭代点的计算开销为:

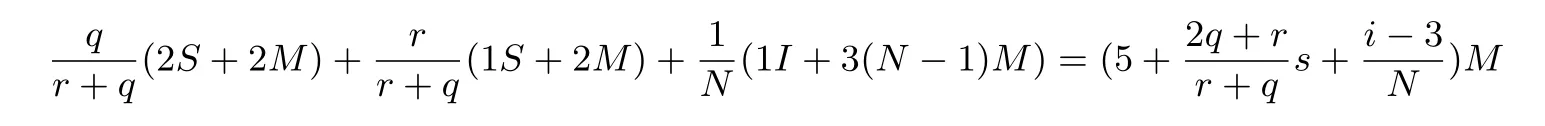
4.4 r+h-混合游走迭代函数实现

Zhang[13]等人提出的r+h-混合游走迭代函数使用了椭圆曲线中的点加和半分运算. 椭圆曲线上的半分运算需要用到1 个解二次方程、1 个开平方根和2 个乘法运算. 在计算ai,bi的时候, 因为除数是2,因此可以看成是移位运算, 在计算机上可以高效实现, 进而忽略计算ai,bi的开销. 因此计算一个半分运算的计算开销为1Sol+1Sqr+2M. 在实现r+h-混合游走迭代函数的程序中, 迭代函数的每一次循环同样是对N个迭代点进行一次迭代, 但是运算与前面两种迭代函数有所不同. 程序首先对每一个迭代点循环执行半分运算, 直到该点的下一次迭代需要执行点加运算为止. 当N个迭代点都执行半分运算后, 此时N个点都需要执行点加运算, 可使用同时逆算法对点加运算进行加速. 所有点执行完点加运算后, 完成迭代函数的一轮循环. 具体r+h-混合游走迭代函数的伪代码如算法7 所示.

可见r+h-混合游走迭代函数平均每个迭代点的计算开销为:

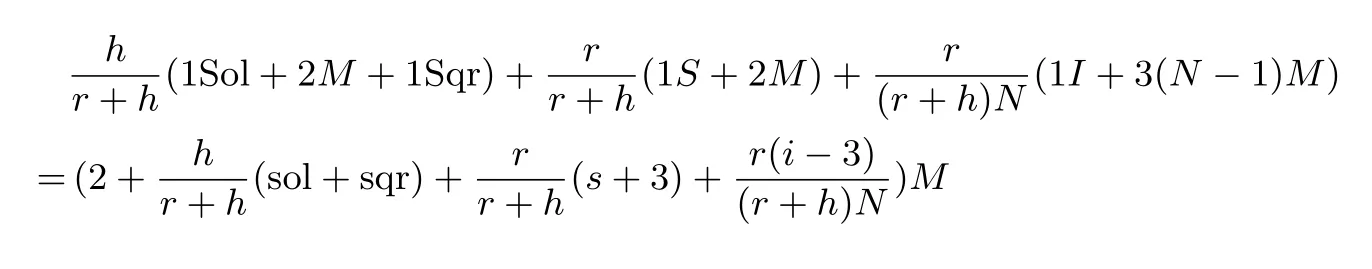
算法7 r+h-混合游走迭代函数Input: N = 256; N 个初始点Pi,i ∈{0,1,··· ,N -1}; 常数r; r 个点Mj,j ∈{0,1,··· ,r-1}; 常数h.Output: ai,bi,aj,bj 满足Pi = aiP +biQ,Pj = ajP +bjQ, 其中Pi = Pj,i ／= j.1 for i = 0 →(N -1) do 2vi ←Pi.x mod (r+h);3while vi ＞= r do 2 Pi;5 4 Pi = 1 ai = (ai&1) ? 1 2(bi +n) : 1 2 ai;6 2 bi;7 2(ai +n) : 1 bi = (bi&1) ? 1 DList.append(Pi,ai,bi) ;8判断DList 中是否有(Pj,aj,bj) 满足Pi = Pj 且i ／= j, 若满足, return ai,bi,aj,bj;10end 11vi ←Pi.x mod (r+h);12end 13 end if Hamming(Pi.x) ＜= 28 then 9 14 同时逆算法求出s-1 i ,i = 0,1,··· ,N -1;15 for i = 0 →(N -1) do 16利用s-1 i 计算Pi = Pi +Mvi;17ai ←ai +mvi;18bi ←bi +nvi;19if Hamming(Pi.x) ＜= 28 then 20DList.append(Pi,ai,bi) ;21判断DList 中是否有(Pj,aj,bj) 满足Pi = Pj 且i ／= j, 若满足, return ai,bi,aj,bj;22end 23 end 24 goto 1

4.5 实验评估

4.5.1 实验环境

本文对三种分布式Pollard rho 进行了仿真实现. 程序基于Intel 指令集的CPU 进行实现, 借助SIMD 指令集对算法进行指令集层面上的优化.算法的仿真实现使用的编程语言是C++,编译器为GCC 9.3.0, 支持C++14 标准; 处理器为: Intel Core i7-7940X CPU @ 3.10 GHz; 操作系统为Ubuntu 18.04.

当椭圆曲线上的点的x轴坐标的Hamming 重量小于13 时, 定义该点为可区分点. 表2 到表4 给出三种迭代函数在不同参数下的随机性量化指标.

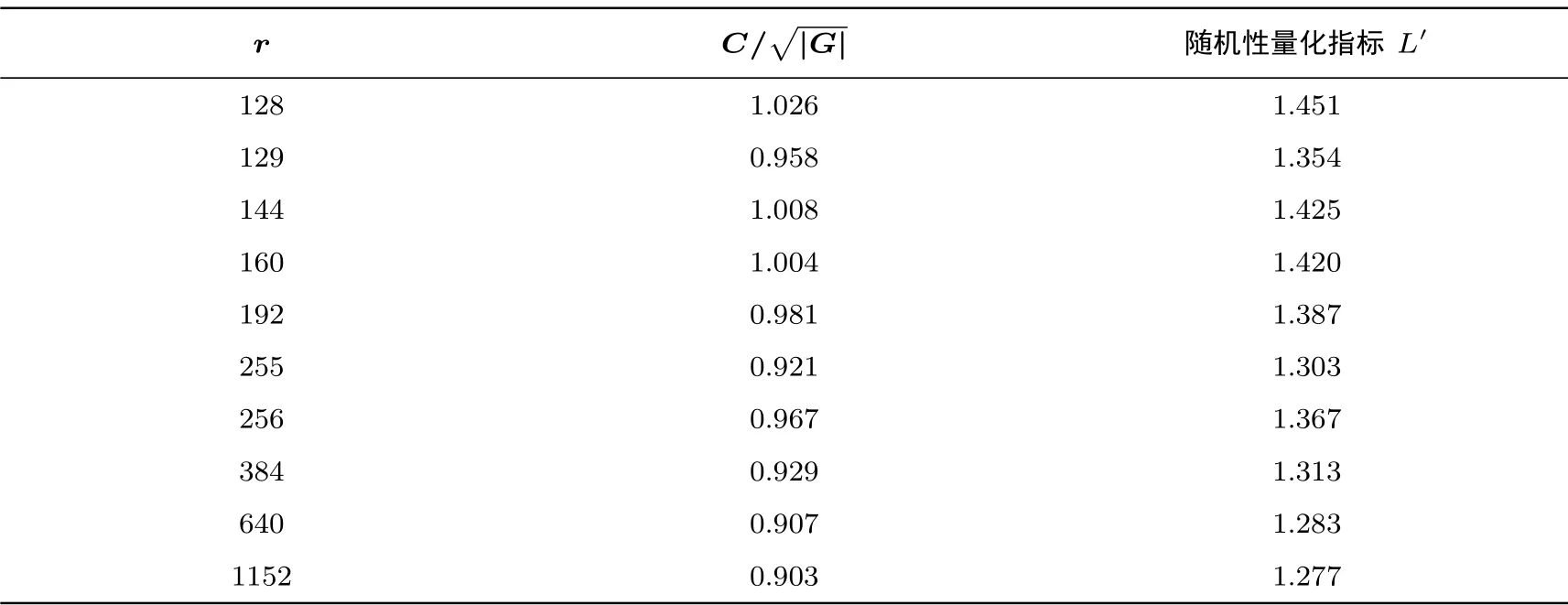
表2 r-加游走迭代函数随机性量化指标Table 2 Quantification index of randomness of r-adding walk

由表3 和表4 可见,当q/r和h/r的比例小于1 的时候,q,h的取值对迭代函数的随机性影响不大;而当比例超过1 时, 两种迭代函数的随机性变化相对明显. 仅测量迭代函数的随机性不足以说明算法的好坏,还需要测量出在不同参数下的分布式Pollard rho 算法的整体效率, 从而得出最优的算法参数. 4.5.3 节将会给出整体效率的测量结果.

表3 r+q-混合游走迭代函数随机性量化指标Table 3 Quantification index of randomness of r+q-mixed walk

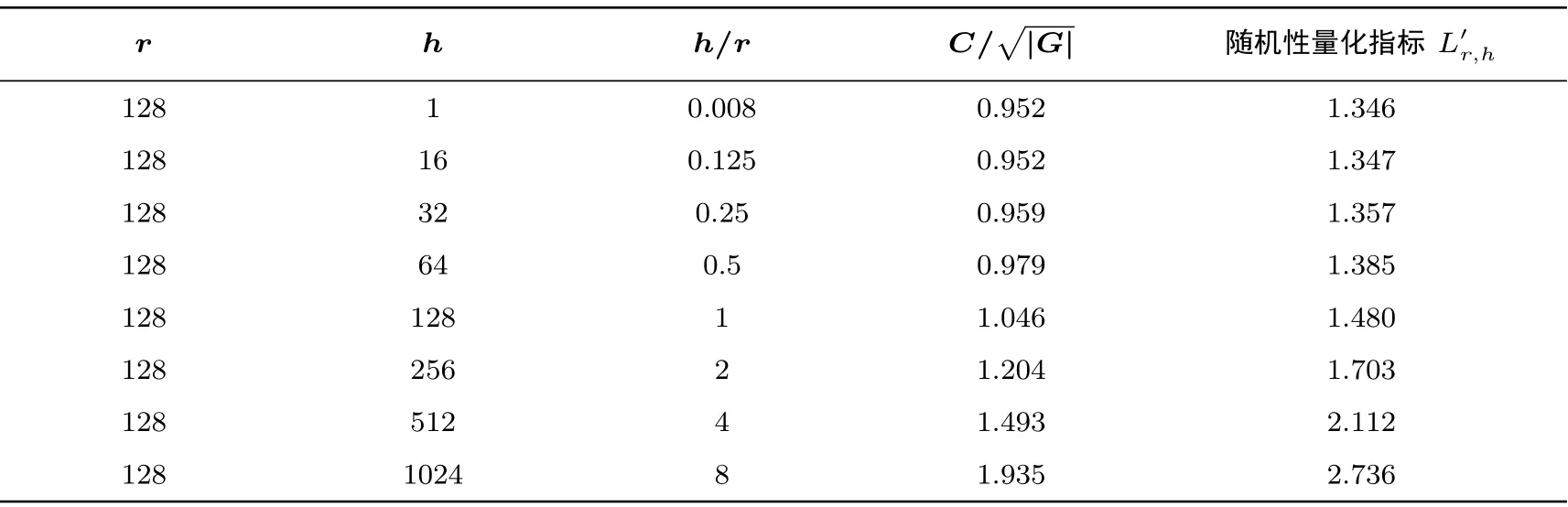
表4 r+h-混合游走迭代函数随机性量化指标Table 4 Quantification index of randomness of r+h-mixed walk

4.5.3 有限域运算效率以及最优分布式Pollard rho 算法

由于求解ECC2-131 的算法与4.5.2 节中求解有限域F241上的ECDLP 所使用的算法是相同的, 因此在迭代函数选择相同参数的情况下, 求解ECC2-131 的Pollard rho 算法的随机性与4.5.2 节测出的相同. 对于ECC2-131, 考虑到在不同的CPU 上程序的运算速度不同, 这可能导致乘法运算与求逆、平方等运算的运行时间的比值不稳定,因此本文在多个CPU 上进行测试来证明有限域多种运算的比值是稳定的.对有限域F2131的每一个算术运算进行100 次开销测试, 每一次测试使该运算执行1000 000 次, 然后取这100 次测试的平均值然后除以1000 000 得到每次运算所消耗的CPU 周期. 表5 为程序使用多种CPU 测试所得到的结果.

表5 不同CPU 上的有限域运算的计算开销Table 5 Computational cost of finite field operations on different CPUs

把乘法运算的时间作为基准, 通过表5 可以计算出有限域上求逆、平方、开平方根和解二次方程这四种运算与乘法运算的时间比例, 具体见表6.

表6 不同CPU 上有限域基本运算时间与乘法运算的比值Table 6 Ratio of the basic operation time to multiplication operation in finite field on different CPUs

有限域的解二次方程这个运算需要用到AVX512 指令集, 而Intel Core i7-9700K @3.60 GHz CPU不支持AVX512 指令集而只支持AVX2 指令集, 因此在该CPU 上的解二次方程运算所用的时间比其它两个CPU 的要长. 本文对三种迭代算法的计算速率的测试在Intel Core i7-7940X @3.10 GHz CPU 上进行测量. 但是总的来说, 由表6 可见, 同一套有限域实现的代码不会因为CPU 选择的不同而导致有限域运算的运算时间比例有明显的差异.

根据表6 所测量得到的数据, 可以对三种分布式Pollard rho 算法的整体效率进行测量, 从而选出最优的情况. 由表6 可得, 式(3) 中的参数取M= 29.179,i= 97.071,s= 0.737,sqr = 1.564,sol = 2.705. 同时逆算法同时计算的有限域元素的个数为N= 256. 测量的方法为统计出迭代100 000 000 个随机点所需要的CPU 周期. 为了避免CPU 被其它进程影响导致测量结果偏大, 本文测量100 次CPU 周期, 去除大于最小值10% 的值后取平均值作为测量结果, 然后把测量结果除以100 000 000 得到每一个迭代点平均计算开销. 由此可得, 三种算法每一个迭代点平均计算开销如表7 所示.

表7 三种分布式Pollard rho 算法每一个迭代点平均计算开销Table 7 Average computational cost of each iteration point of the three distributed Pollard rho algorithms

由表7 可见, 仿真测试值与理论值相比有一定的误差, 而且都是仿真测量值比理论值要大. 这个误差的存在是合理的, 因为开销表达式没有包含有限域加法运算和计算ai,bi的开销, 而且程序在编程实现的过程中会有额外的开销, 比如循环语句、条件判断语句和函数调用开销等. 与此同时, 仿真测量值的变化趋势没有完全按照理论值的变化而变化, 这是由于在不同的r,q,h参数下, 程序的优化情况有所不同. 比如r+q-混合游走迭代函数在r= 128,q= 1024 的情况下, 相比于r+h-混合游走迭代函数在h= 64 和h=128 的情况运算速率更高, 这是因为r=128,h=1024 的参数更有利于程序的优化和执行. 从整体效率上看, 基于r+q-混合游走迭代函数或r+h-混合游走迭代函数的分布式Pollard rho 算法都是当r固定不变时随着参数q和h的增大而整体效率的值增大, 即意味着算法的整体效率更低.

通过表5 和表6 的有限域运算的测量结果, 从理论上进行分析可知, 基于r-加游走迭代函数的分布式Pollard rho 算法所需要的每一轮迭代的计算开销是最小的, 而且在程序实现上也能达到最优效果, 其整体效率也是最优的. 文献[13] 中提到在不使用同时逆算法的情况下, 半分运算与倍点运算相比有非常大的计算优势, 因此使用半分运算可以获得非常高的提速效果. 然而, 在使用同时逆算法对求逆运算进行加速的时候, 半分运算的优势会被削弱. 理想情况下,r-加游走迭代函数的迭代时间为

5 ECC2-131 求解评估与分析

本节在实验仿真层面对求解ECC2-131 的速度与开销进行评测. 通过在工作站和天河二号超级计算机上分别进行算法开销的评测. 自椭圆曲线算法提出以来, ECDLP 的求解就一直在被研究. 与此同时, 计算机CPU 指令集的发展也为ECDLP 的求解带来了非常大的帮助. 因此本文选取算法上随机性好, 整体效率较优, 软件实现能做到高效实现的基于r-加游走的分布式Pollard rho 算法求解ECC2-131. 软件实现的过程中r-加游走迭代函数的参数根据表7 中整体效率较优的结果, 并考虑r不能取太大以免导致内存访问过于频繁从而降低效率, 因此取r=255.

5.1 工作站上的ECC2-131 求解

本节的分布式Pollard rho 算法使用C++ 进行实现, 程序支持C++14 标准. 分布式Pollard rho算法的实现借助SIMD 指令集进行优化. 本节所使用的工作站的配置为: Intel Core i7-7940X @3.10 GHz CPU; 操作系统: Ubuntu 18.04.

5.2 天河二号超级计算机上的ECC2-131 求解

超级计算机能执行需要大量计算量的程序. 它主要的优势是有极大的数据存储容量和非常高的数据处理速度, 因此在超级计算机上解决ECDLP 就成为了可能. 本文使用天河二号超级计算机进行求解, 首先计算出一部分ECC2-131 的可区分点, 测试在天河二号中求解ECC2-131 的程序的性能. 然后通过测试的结果分析出使用天河二号求解ECC2-131 的速度以及可行性.

5.3 性能分析

Daniel 等人[16]的测量结果指出,在Core 2 Extreme Q6850 CPU 上进行ECDLP 的求解,可以做到单核消耗533 个CPU 周期运行一轮迭代.在他们的软件程序中,有限域使用多项式基表示,而有限域的数据结构使用Bitslice[16]转换得到. 在Bitslice 转换后的数据结构下, 有限域的平方、乘法和求逆运算与非Bitslice 的形式有很大的不同. 在CPU 层面上, 天河二号中单个节点单核的计算性能与Core 2 Extreme Q6850 CPU 单核的计算能力相近. 因此忽略CPU 性能对两种算法所带来的影响, 本文实现的程序在天河二号中能做到单核单线程消耗418.2163 个CPU 周期完成一轮迭代, 与Daniel 等人的结果相比有21.5%的效率提速.

考虑到CPU 技术的不断发展, 本文在Intel Core i7-7940X @3.10 GHz CPU 上能做到每个迭代花费229.8463 个CPU 周期, 与Daniel 等人的结果相比有了56.9% 的效率提升. 而且本文算法的软件实现对于CPU 的性能要求比较高, 用到了Intel CPU 中的PCLMULQDQ 指令, 近几年CPU 不断的发展, PCLMULQDQ 指令所消耗的时间越来越小, 这也是为什么同一套软件在Intel Core i7-7940X @3.10 GHz CPU 和在天河二号中性能有明显的差距.

6 总结

本文重新分析了基于r-加游走、r+q-混合游走和r+h-混合游走迭代函数的三种分布式Pollard rho算法的计算效率, 并对这三种算法在软件上进行快速实现. 本文发现基于迭代函数为r-加游走的分布式Pollard rho 算法在理论分析和仿真测试中与其它两种算法相比有着更高的效率.

与此同时, 本文在有限域F2131中找出最优不可约多项式, 通过域同构诱导出椭圆曲线的同构从而得出椭圆曲线群的同构. 使用同构后的有限域和椭圆曲线进行编程实现, 程序的有限域乘法运算有11.23%的提速, 模运算有11.29% 的提速. 本文在Intel Core i7-7940X @3.10 GHz CPU 和天河二号超级计算机上对求解ECC2-131 的软件程序进行效率测试, 发现目前为止, 计算ECC2-131 仍然是一个困难的问题.即使使用天河二号所有CPU 计算资源, 也需要消耗12.96 亿核时, 花费1.296 亿元, 运算约125.60 天才能计算出ECC2-131. 这在时间和经济上不实际, 可见ECC2-131 目前仍然无法被解决.