基于变模与自更新密钥矩阵的高效RFID 安全认证协议*
2022-05-09雷雪梅
王 艳, 雷雪梅, 高 通
1. 内蒙古大学, 呼和浩特 010021
2. 哈尔滨工业大学, 哈尔滨 150001
1 引言
中国工业和信息化部于2017 年发布的《物联网“十三五” 规划》文件中指出, 我国物联网技术在物流、环保、医疗、交通等多个领域均已得到广泛应用. 而RFID (radio frequency identification) 作为实现物联网的关键技术, 以其特有的无接触、可同时识别多个物体等优点在物联网应用领域中大放异彩.
但是随着RFID 应用日益广泛, 其安全与隐私问题也随之而来. 如用户标签被秘密定位并追踪, 使个人隐私遭到破坏; 又如物品的详细信息在传输过程中易受攻击, 从而导致物品隐私信息泄露等[1]. 同时,RFID 安全系统不仅要满足抵御攻击、数据认证、访问控制等要求, 而且需要注重RFID 系统标签的计算能力、存储空间和可编程性等限制所导致的无法利用高复杂度的加解密算法保证自身安全的问题等[2]等.
目前针对RFID 的安全策略主要可分为两大类: 物理安全机制和软件安全机制. 物理安全机制主要包含kill 标签、法拉第笼、主动干扰、阻止标签等[3], 软件安全机制主要以密码算法和密码协议为基础. 目前, 现有的RFID 认证协议依据标签的计算能力可被分为以下四类:
(1) 重量级认证协议: 一般使用较为完善和安全的加密方法, 包括基于对称密钥的RFID 安全协议以及非对称密钥算法的RSA 方案、椭圆曲线密码机制ECC 等. 目前应用比较成熟的对称加密算法有DES 数据加密算法(data encryption standard)[4]以及AES 高级加密标准(advanced encryption standard)[5]等. 对称密钥指阅读器和标签之间共享同一个密钥, 该方法的缺点是一旦标签的密钥被泄露就会影响整个系统的安全性[6]. 非对称密钥算法又称为公钥密码算法、双钥密码算法, 这类算法是基于数学的密码理论技术[7], 例如RSA 算法[8]是一种基于数论构造双钥的方法, 它的安全依赖于数论大整数分解的困难性, 密钥长度一般介于1024 bit 到2048 bit 之间. 再如ECC[9]算法基于离散对数, 数学理论复杂、工程上应用较困难, 但其破译求解难度基本是指数级的, 可满足所期望的安全强度. 综上, 使用重量级认证协议对标签的计算能力和存储资源要求很高, 因此不适合大规模推广使用.
(2) 简单级认证协议: 一般指标签内部可支持伪随机数发生器以及基于哈希函数的安全机制. 常见的有hash lock 协议、随机hash lock 协议、hash chain 协议等. hash lock 协议[10]对密钥进行明文传输且metaID 保持不变, 这样容易被记录跟踪; 阅读器与标签之间传输的数据未经加密, 攻击者很容易获得Key 和ID 值, 故该协议还易受到假冒攻击、重放攻击. 随机hash lock 协议[11]虽有改进, 可以防跟踪, 但仍易遭到假冒攻击、重放攻击等. 而且在该协议中, 阅读器要计算数据库全部ID 的hash 值, 计算量复杂, 易受拒绝服务攻击. Hash chain 协议[12]中秘密值虽不断更新, 但双方秘密值更新不同步, 即该协议无法抵挡去同步化攻击.
(3) 轻量级认证协议: 一般指使用PRNG 和简单函数对RFID 系统加密的协议. 文献[13] 中提出HB 协议, 以及后续改进提出的HB+ 协议, 均没有对阅读器进行安全验证, 因此易受到中间人攻击和跟踪攻击.
(4) 超轻量级认证协议: 一般指仅包含一些简单的位运算操作(例如与、或、非、异或等) 的认证协议. 文献[14] 中提出的LMAP 协议仅仅采用简单的位运算操作, 虽然它的私钥不断更新, 但由于运算简单, 容易受到跟踪攻击、同步攻击和拒绝服务攻击等.
由上述分析可知, 重量级以及简单级认证协议对标签的存储性能和计算能力提出了挑战, 超轻量级认证协议虽然满足低计算量条件, 但其安全性较弱. 为此, 根据RFID 系统的特点以及安全需求, 已有学者提出一系列轻量级安全协议, 本文主要研究基于密钥矩阵的轻量级安全认证协议. 例如在文献[15] 中提出一种基于密钥矩阵的RFID 安全认证协议, 该协议采用双密钥矩阵进行了双向身份认证, 具有标签匿名性、前向安全性等特点, 但是该协议的不足之处是: 第一, 标签和数据库的密值更新不同步, 容易受到去同步化攻击; 第二, 标签存储信息量较大. 在文献[16] 提出一种自同步密钥矩阵RFID 安全协议, 解决了文献[15] 中“标签中信息和后台数据库中信息没有同步更新” 的问题, 但仍没有解决标签存储信息量大的问题. 在文献[17] 中提出一种基于动态共享密钥的移动RFID 双向认证协议, 该协议中标签不能对阅读器的合法性进行验证, 让攻击者有机可乘假冒合法阅读器查询标签, 即该协议无法抵抗假冒攻击.
为此, 本文在文献[18] 的基础上, 提出一种基于变模且自更新密钥矩阵的轻量级RFID 安全认证协议, 并利用Winograd 算法对密钥矩阵的加解密过程进行加速设计, 以此提高标签认证的实时性, 经分析,该协议可有效抵抗多种典型攻击, 且具备低复杂性和适合低成本标签的特点.
2 基于变模与自更新密钥矩阵的RFID 安全认证协议的提出
首先给出密钥矩阵算法涉及的数学定义.
定义1 若一个n阶矩阵A的所有元素均为整数, 则称A为n阶整数矩阵.
引理1 若p为正整数,a为整数, 且p与a互素, 则同余方程ax ≡1 mod(p) 在模p意义下存在唯一解, 即存在正整数a′<p, 使aa′≡1 mod(p).
定义2 若A、B为整数方阵, 且A×B ≡Emod(p), 其中E为单位矩阵, 则称B是A的模p逆矩阵.
不难证明,n阶整数方阵A存在模p逆矩阵的条件是矩阵A的行列式的值与p互素. 根据上述定义,对于一个给定的n阶整数矩阵A, 若其行列式的值与整数p互素, 则可利用初等变换方法求得A矩阵的模p逆矩阵B, 利用A、B与p可建立密钥矩阵的加密过程与解密过程如式(1)和式(2)所示.

其中E(),D(),t,c分别代表加密过程、解密过程、明文以及密文.
根据上述加解密过程可知, 在传统的基于密钥矩阵的RFID 安全认证协议中, 为提高协议安全性的可能做法是直接存储多组加密、解密矩阵. 相比单一的密钥矩阵, 这种预共享多组密钥矩阵的方式虽然可以提高加密算法的安全性, 但也消耗了标签大量的存储空间.
为了在不增加原有密钥矩阵的存储量的前提下同时提高协议的安全性, 本文提出变模密钥矩阵加密算法, 将原有密钥矩阵加密算法的常量模p扩展为变量模p, 在标签认证过程中通过模的自更新, 弱化明文与密文之间的相关性, 提高认证协议的安全性.
下面给出变模密钥矩阵可行性的证明过程.
定理1 若正整数a与p互素, 则a与q互素, 其中q为p的整数约数.
该定理可通过基本的数论理论直接得到. 这意味着, 对于整数矩阵A, 其行列式与模p互素, 那么对于整数q, 其中q为p的整数约数, 满足A的行列式与模q也互素. 再结合定义2, 可以得到整数矩阵A存在模q逆矩阵. 随后将证明整数矩阵A的任意模q(q为p的任意约数) 逆矩阵是相同的, 这可以表述为定理2.
定理2 若A、B为整数方阵, 使得:A×B ≡Emodp,E为单位矩阵, 即B为A的模p逆矩阵,那么B同时为A的模q逆矩阵, 其中q为p的整数约数.
证明: 由于A×B ≡Emodp, 那么A×B ≡pC+E, 其中C为任意整数矩阵. 又由于q为p的整数约数, 即p=aq, 其中a为正整数. 那么A×B=aqC+E=qD+E, 其中D为整数矩阵. 因此,可以得到A×B ≡Emodq.
根据上述证明, 可以发现加密矩阵A与解密矩阵B可以利用模p或者模q实现加密与解密过程, 其中p为合数,q为p的整数约数. 虽然实现了模的自更新, 但不同模值下所对应的加密、解密矩阵是相同的, 此时, 密钥矩阵的固定不变有损RFID 安全认证协议的安全性. 为此, 考虑利用矩阵的初等变换实现密钥矩阵的自更新. 首先以初等行变换为例说明如何实现密钥矩阵的自更新, 初等列变换同理. 初等行变换包含以下三种变换:
(1) 以一个非零的数乘矩阵的某一行;
(2) 把矩阵中的某一行的k倍加到另一行;
(3) 互换矩阵中两行的位置.
考虑本文RFID 安全认证协议是针对低成本标签提出的, 对于低成本标签来说, 实现乘法操作相对于实现加法操作更难更耗时, 因此取消乘法操作, 同时在第(2) 种初等行变换中取k=1, 这样需要在标签中执行的矩阵的初等行变换只有两种, 即:
(a) 矩阵的某一行加到另一行;
(b) 互换矩阵中两行的位置.
下面给出经过初等变换的密钥矩阵可实现加解密过程的可行性论证.
由矩阵的初等变换可知, 矩阵的某行(列) 加另一行(列), 该矩阵对应的行列式的值不变. 互换矩阵中的某两行(列) 一次, 其对应的行列式的值加一个负号, 互换矩阵中的某两行(列) 两次, 或者, 先互换一次行(列), 再互换一次列(行), 两个负号抵消, 其对应的行列式的值还是原矩阵对应的行列式的值. 又根据定义2,n阶整数方阵A存在模p逆矩阵的条件是矩阵A的行列式的值与p互素. 由于矩阵经过上述初等变换后其对应的行列式的值不变, 即该值仍与模p互素, 即经过上述初等变换的新的密钥矩阵同样可建立如式(1)和式(2)所示的密钥矩阵加解密过程.
根据自更新密钥矩阵可行性论证可知, 构建n阶加密矩阵初等变换方式索引表可分为“列交换两次”、“行交换两次”、“行相加”、“列相加”、“先换行(列) 再换列(行)” 等五种情况, 根据n阶加密矩阵初等变换方式索引表可以相应构建出n阶解密矩阵初等变换方式的逆变换索引表. 初始加密、解密矩阵可通过查找初等变换方式索引表、相应的逆变换索引表, 形成新的加密、解密矩阵, 得到的新的密钥矩阵更新原来初始密钥矩阵的存储单元, 不需要额外增加其他存储空间来存放新的密钥矩阵. 即标签仅需要存储一个初始加密矩阵和一个初始解密矩阵的空间, 通过初等变换, 即可实现多次加解密过程.
考虑到更高阶的密钥矩阵的初等变换方式众多, 其中会涉及多次两行(列) 相加, 为避免密钥矩阵的元素数值过大而溢出, 将初等变换后的密钥矩阵中的元素按照模p处理, 这样所有元素的值将不大于p.
综上, 密钥矩阵的自更新仅涉及加法和互换操作, 这对低成本标签是可实现的, 同时, 密钥矩阵自更新在不额外增加存储空间的前提下, 实现了密钥矩阵的多样性, 提高了密钥矩阵加密算法的安全性.
2.1 构建基于变模与自更新密钥矩阵的RFID 安全认证协议
根据变模且自更新密钥矩阵加密算法, 构建RFID 系统的安全认证协议, 如图1 所示. 该协议每一次认证都会更新当前的密钥矩阵模值, 使得密钥矩阵模值具有强无关性, 同时利用矩阵初等变换方法实现密钥矩阵自更新, 提高了RFID 安全认证协议的安全性.

图1 基于变模与自更新密钥矩阵的RFID 认证协议Figure 1 RFID authentication protocol based on variable modulus and self-updating key matrix
基于变模与自更新密钥矩阵的高效RFID 安全认证协议的初始条件如下:
(1) 本协议假设阅读器与后台数据库之间的通信是安全可靠的;
(2)标签、阅读器、服务器内需预先存储的元素如图1 所示. 其中,图1 中虚色框中以二阶矩阵为例,说明标签和阅读器内需要预先存储的“加密矩阵初等变换方式索引表”、“解密矩阵初等变换方式的逆变换索引表”、“模p的整数约数集合f(p) ” 的构建方法. 这里应注意, 二阶密钥矩阵经过“行交换两次”、“列交换两次” 之后会回归为初始密钥矩阵, 所以这两列为空, 但对于三阶以及更高阶密钥矩阵, “行交换两次”、“列交换两次” 的初等变换方式可形成多种不同的密钥矩阵. 此外, 由于模p的整数约数一定包含模p本身, 所以在存储模p的整数约数时, 为了节省存储空间, 不必再存储模p本身, 模p的其他整数约数按照从小到大的顺序排列.
RFID 安全协议的认证步骤如下:
(1) 阅读器向标签发送Query 指令.
(2) 标签响应阅读器, 使用内部随机数发生器产生的随机N、加密矩阵A以及模p根据公式(1)对秘密值S进行加密, 记作E(N ‖S,A,p).
(3) 标签将E(N ‖S,A,p) 发送给阅读器.
(4) 阅读器根据公式(2)对标签发来的密文进行解密, 得到S.
(5) 阅读器将S发送给后台数据库.
(6) 后台数据库查询所有S, 若查询不到, 记为非法标签, 结束认证. 若可查询到, 后台数据库生成新的秘密值Snew.
(7) 后台数据库向阅读器发送新的秘密值Snew.
(8) 阅读器收到新的秘密值Snew后保存, 并利用Snew、加密矩阵A、模p根据公式(1)对N+1 进行加密, 记作E(N+1‖Snew,A,p).
(9) 阅读器将E(N+1‖Snew,A,p) 发送给标签.
(10) 标签收到来自阅读器的E(N+ 1‖ Snew,A,p) 后, 根据公式(2)解密得到N+ 1‖ Snew, 验证随机数N, 若N正确, 证明阅读器合法, 则接受新秘密值Snew, 否则认证失败. 标签计算mod(Snew,Nc) 的值作为在集合{q|q ∈f(p)}的序号, 进一步确定密钥矩阵的模值q, 同时利用mod(Snew,Nc) 的值作为在矩阵初等变换方式索引表中的序号, 决定用哪种初等变换方式生成新的加密矩阵Anew, 标签利用模q和Anew根据公式(1)对敏感信息ID 加密, 记作E(ID,Anew,q).
(11) 标签将E(ID,Anew,q) 发送给阅读器.
(12) 阅读器收到E(ID,Anew,q) 后, 利用先前保存的Snew计算mod (Snew,Nc) 的值确定模和矩阵的初等变换方式, 采取该初等变换方式的逆变换就可确定解密矩阵, 利用解密矩阵根据公式(2)对E(ID,Anew,q) 解密, 获得敏感信息ID.
其中E() 代表加密过程, 表示认证过程所传输的均为密文,S代表秘密值, 秘密值的取值会影响密钥矩阵模值的选取,N代表随机数,A为加密矩阵,Nc代表集合f(p) 中元素的个数, “mod(Snew,Nc) =Snew%Nc”, 表示Snew除以Nc所得的余数, “‖” 代表字符串连接符号.
3 基于变模与自更新密钥矩阵的RFID 安全认证协议的形式化分析
BAN 逻辑被称为“密码协议形式化分析之父”. 它是一种基于知识和信仰的形式逻辑分析方法. 本文采用BAN 逻辑分析所提出的RFID 安全认证. 本次推理用到的BAN 逻辑推理规则:

上述四条推理规则中所涉及的基本术语如下:P、Q表示一般意义上的主体,X、Y表示一般意义上的观点,K表示一般意义上的加密密钥, (X,Y) 表示X和Y的连接.P|≡X表示P相信X,P◁X表示P收到过X, #(X) 表示X是新鲜的,Q|~X表示Q发送过X,Q|⇒X表示Q对X有管辖权.
使用BAN 逻辑分析该RFID 安全认证协议的步骤如下: 本协议主体为: 标签T 和阅读器R. 该协议的理想化模型:

取key 表示本协议中标签和阅读器之间共享的加密矩阵A及Anew、加密所用到的模值p或q, 则初始假设为:


逻辑推理过程:
(1) M1、A2 根据规则R1 可得R|≡T|~{N||S}记作L1;
A3 根据规则R2 可得R|≡#(N||S) 记作L2;
L1、L2 根据规则R3 可得R|≡T|≡{N||S}记作L3;
L3 和A5 根据规则R4 可得R|≡(N||S) 即得G1. 推理完毕.
(2) M2、A1 根据规则R1 可得T|≡R|~{N+1||Snew}A,p记作W1;
A4 根据规则R2 可得T|≡#(N+1||Snew) 记作W2;
W1、W2 根据规则R3 可得T|≡R|≡{N+1||Snew}记作W3;
W3 和A6 根据规则R4 可得T|≡(N+1||Snew) 即得G2. 推理完毕.
(3) M3、A2 根据规则R1 可得R|≡T|~{ID}记作Y1;
A7、Y1 根据规则R3 可得R|≡T|≡{ID}记作Y2;
Y2 和A8 根据规则R4 可得R|≡(ID) 即得G3. 推理完毕.
通过BAN 逻辑推理过程, 最终能够推理出目标G1、G2、G3, 即说明本文提出的基于变模与自更新钥矩阵的高效RFID 安全认证协议能够达到预期目标.
4 基于变模与自更新密钥矩阵的RFID 安全认证协议的加速设计
由公式(1)和(2)可知, 密钥矩阵的加解密过程主要涉及矩阵乘法和取模运算. 首先, 对于标签来说, 集合f(p) 是预先存储在标签内的, 即模p的整数约数q的个数对标签是已知的, 所以取模运算次数对于标签来说是计算量较小的操作. 其次, 经计算, 本文所提出的基于变模与自更新密钥矩阵的RFID 安全认证协议, 其加密过程共涉及n2次乘法与n(n-1) 次加法. 由于乘法运算相比加法运算复杂得多, 有必要减少其乘法运算次数以提高加密速度. 故本文引入Winograd 算法[19,20], 通过减少密钥矩阵加解密过程中的乘法运算量提高算法实时性. 对于加密矩阵A模p, 其第i行j列的元素表示为Aij, 那么可应用Winograd 算法对明文t进行加密如下所示:


表1 不同长度的明文加密或解密过程的乘法与加法运算次数对比Table 1 Comparison of number of multiplication and addition operations in different lengths of plaintext encryption or decryption
5 变模与密钥矩阵初等变换结合起来对标签存储空间节省情况与安全性分析
一般情况下, 认为阅读器和后台服务器的存储空间都远强于标签, 因此本协议需要重点考虑变模和初等变换结合之后对标签的存储变量个数的节省情况.
首先说明由常量模扩展为变量模之后, 标签内需要存储的模p的整数约数个数情况.
在前面变模密钥矩阵可行性的证明过程中指出, 模p为合数,q为p的整数约数. 由于合数众多, 不能一一举例, 又因为最小的合数是4, 因此在本文中首先利用C 程序找出4 到100 以内的所有合数以及每一个合数所对应的整数约数的个数, 如表2 所示.
由表2 可见, 不同合数的整数约数个数可能相同, 比如4、9、25、49 这四个合数的整数约数个数都是3 个. 由于标签需要存储的是p的整数约数集合f(p), 因此对于具有相同整数约数个数的不同合数来说,在标签中需要存储的f(p) 集合元素个数是相同的. 故本文在整数约数个数相同的合数中, 只取其中一个合数作为代表, 来举例说明标签需要预存储的变模变量的个数.

表2 4 至100 以内的所有合数以及每个合数对应的整数约数个数Table 2 All composite numbers from 4 to 100 and corresponding integer divisor for each composite number
表3 中选取了比较典型的12 个合数, 并列出他们对应的整数约数以及个数. 结合前文在描述协议认证过程中已经取Nc表示标签需要存储的模p的整数约数个数, 由协议的初始条件可知,Nc值会比模p的整数约数总个数Num 少1, 即Nc=Num-1.

表3 12 个典型合数所对应的整数约数以及其整数约数个数Table 3 Integer divisor corresponding to a typical composite of 12 and number of integer divisor
在表4 中对比说明了不同的变模个数Nc以及不同的明文长度n使用变模密钥矩阵算法前后标签需要预存储的总变量个数情况, 表格中W1 表示使用变模密钥矩阵算法后标签需要预存储的总的变量个数,W2 表示直接存储多个密钥矩阵时标签需要预存储的总的变量个数, 取S= (W2-W1)/W2×100%表示使用变模密钥矩阵算法前后节省标签存储空间的百分比. 例如, 当使用变模密钥矩阵算法时, 标签内需要存储明文长度n、n阶加密矩阵变量个数n2、n阶解密矩阵变量个数n2、一个模值p、标签需要存储的p的整数约数个数即Nc个变量以及一个使用Winograd 算法过程中预先计算的变量mi, 即W1=n+n2+n2+1+Nc+1=n+2n2+Nc+2. 而当不使用变模密钥矩阵算法即直接存储多个密钥矩阵并想同样达到Num 种可能性时, 需要存储Num 种n阶加密矩阵变量个数n2以及Num 种n阶解密矩阵变量个数n2, 即W2=Num×2n2. 利用MATLAB 程序计算不同明文长度n以及不同模p下使用变模密钥矩阵算法前后的标签需要预存储的变量个数, 即得到表4.
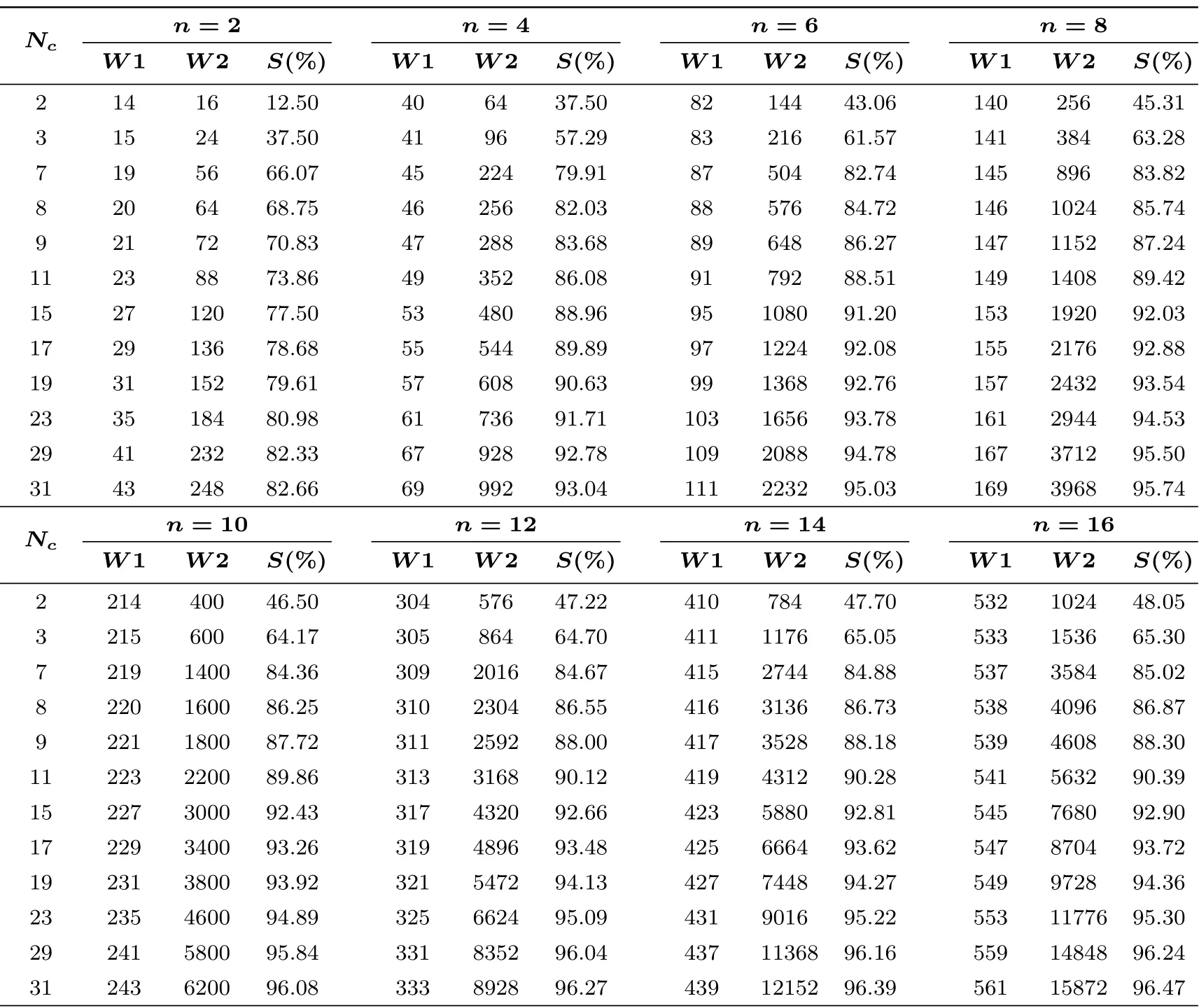
表4 使用变模密钥矩阵算法前后标签需要预存储的总变量个数情况对比Table 4 Comparison of total number of variables pre-stored in tags before and after using variable mode key matrix algorithm
根据图1 可知, 变模和初等变换结合后, 可完成加解密次数如式(5)所示:

因此根据图1 中的构建方法可知, 不同明文长度n, 需使用不同的n阶密钥矩阵加解密, 相应密钥矩阵初等变换方式索引表及其对应逆变换索引表的元素数量不同, 即X不同. 由于更高阶密钥矩阵的初等变换方式众多, 不能一一列举, 故本文只列举了二阶、三阶密钥矩阵初等变换方式索引表中的可选择数量,即当n=2 时,X=5; 当n=3 时,X=33. 在不同的n、Nc下可得到不同的K1、K2, 具体如表5 所示.
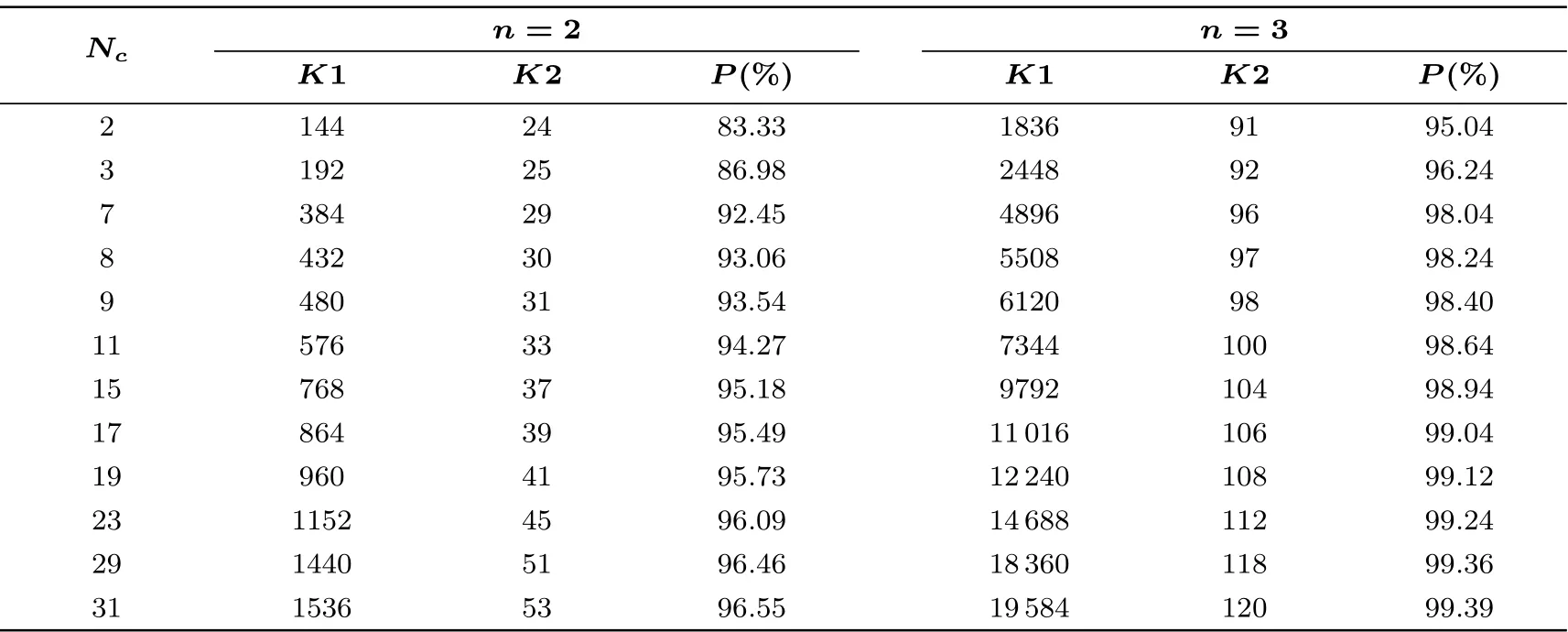
表5 变模和初等变换结合起来对标签内预存储变量个数的节省情况对比Table 5 Saving comparison of number of pre-stored variables in tag by combining variable modulus and elementary transformation
对比表4、表5 可知, 在相同明文长度n、相同Nc的情况下, 变模和初等变换结合起来之后, 节省的标签需要存储变量个数的百分比均有所提高. 可见无论是变模, 还是密钥矩阵的初等变换, 均节省了密钥存储空间, 而且变模与密钥矩阵的自更新使加解密过程的安全性有所提高.
6 基于变模与自更新密钥矩阵的高效RFID 安全认证协议的安全性分析
本文协议安全性能分析与对比如表6 所示.

表6 协议安全性能比较Table 6 Protocol security performance comparison
(1) 双向认证: 在协议认证过程中, 本协议通过秘密值和随机数, 首先分别认证阅读器和标签是否合法, 确认阅读器和标签的合法身份信息后再进行敏感信息处理. 由于认证信息均被加密和随机化, 故本协议做到了标签与阅读器的双向认证.
(2) 跟踪攻击: 本协议在认证过程中发送的数据均包含随机数和秘密值, 且标签和阅读器之间的密钥矩阵是由秘密值决定, 加密解密过程中密钥矩阵的模参数和密钥矩阵都是可自更新的, 因此保证了所有认证过程中, 标签和阅读器互相反馈的信息均为随机的, 故本协议中攻击者无法对标签进行定位跟踪.
(3) 拒绝服务攻击: 若攻击者在阅读器和标签之间大量施加噪声干扰信号, 有可能导致信道阻塞, 或者由于大量的数据请求而导致认证负载过大系统瘫痪, 造成拒绝服务攻击. 而本协议先查询后台数据库Index, 若查询不到记为非法标签则结束认证. 这种先查询后认证的方式有效抵御了拒绝服务攻击.
(4) 假冒攻击: 分情况讨论: 第一, 当攻击者企图伪装成标签向阅读器发送E(N ‖ S,A,p) 时, 阅读器查询后台数据库找不到对应的秘密值S, 随后记为非法标签; 第二, 当攻击者伪装成阅读器向标签发送E(N+1‖ Snew,A,p) 时, 标签解密, 验证随机数N不正确, 因此得知阅读器非法. 故该协议能够防范假冒攻击.
(5) 中间人攻击: 假设攻击者想实施中间人攻击, 则攻击者需要知道阅读器和标签之间发送的随机数和秘密值, 甚至密钥矩阵, 并能够造出可以通过双方认证的数据, 但是本协议每一次认证都会更新秘密值,密钥矩阵的模参数是根据秘密值更新的, 密钥矩阵本身根据秘密值选取不同的初等变换方式不断更新, 且标签内部具有伪随机数发生模块, 攻击者无法通过标签和阅读器的身份认证, 因此避免中间人攻击.
(6) 重放攻击: 本协议中, 标签和阅读器之间的认证数据由于含有随机数而一直保持新鲜性, 且随着秘密值的更新而更新密钥矩阵, 攻击者无法从上一轮截获的信息中推导出当前的数值, 而且即使攻击者获得当前密钥矩阵的模q, 攻击者也不可能根据约数q推出模p进而推出密钥矩阵, 因为同一q值可能是多个模p 的整数约数, 例如24 同时是p= 24 和p= 48 的整数约数, 不能根据q= 24 推出p= 24 还是p= 48, 而且秘密值的不同影响密钥矩阵初等变换方试的选择, 因此也不能推出密钥矩阵的值, 故攻击者无法进行重放攻击.
(7) 去同步化攻击: 假如攻击者阻拦或者修改了阅读器与标签通信的一部分或者全部数据, 使两者变得不同步, 遭遇去同步化攻击. 但是本协议都是在认证通过以后才进行通信, 且阅读器中建立了标签秘密值Index, 保存上一轮的秘密值S, 即保留着密钥矩阵, 可以确保即使当前认证失败, 可以用上一轮密钥矩阵再次计算, 以此来抵抗去同步化攻击.
(8) 前向安全性: 本协议认证过程中所传输的数据均由随机数N 和秘密值S直接参与, 模参数和密钥矩阵均可自更新, 因此攻击者不可能通过本次认证的数据计算得出上一次的认证数据. 因此协议具有前向安全性.
7 结束语
通过运算次数效率对比分析表明, 本文所提出的基于变模密钥矩阵的RFID 安全认证协议通过Winograd 算法加速后, 大幅度减少标签内协议运算量, 从而提高标签认证效率; 经过密钥矩阵模参数的在线更新节省了低成本标签的存储空间, 通过矩阵初等变换方法使密钥矩阵可实现自更新, 更提高了协议的安全性. 经BAN 逻辑分析与协议安全性分析得知, 该协议能够实现双向认证且有效抵抗跟踪攻击、拒绝服务攻击、假冒攻击、中间人攻击、重放攻击、去同步化攻击等多种典型攻击, 能够较好的满足RFID 系统所需的各项安全性. 此协议通过密钥矩阵模参数以及密钥矩阵本身的在线更新, 实现了不以增加密钥矩阵的额外存储量为代价去提高协议安全性. 因此本文所提出的RFID 安全认证协议具有低计算量、低存储量的优势.
