管路焊接结构的随机振动疲劳损伤分析
2022-05-09李志强张梦妍
李志强,于 洋,刘 艳,刘 艺,张梦妍
(1. 北京强度环境研究所 可靠性与环境工程技术重点实验室,北京 100076;2. 北京电子工程总体研究所,北京 100854; 3. 北京强度环境研究所,北京 100076)
0 引言
管路结构广泛应用于飞行器储箱增压、推进剂输送、压力测量、气封吹除及伺服排焰等。由于焊接结构具有良好的连接性,易于加工,便于采用自动化生产,管路接头大量使用了焊接连接形式。然而,受飞行器结构限制,大部分管路的空间布局不规则,边界条件复杂;同时,管路工作过程中承受内压、高低温、振动及冲击等载荷。这些都会导致焊接部位应力状态复杂,易发生疲劳失效,严重影响飞行器的可靠性。
在航空领域,针对管路结构疲劳失效分析已开展很多研究工作。针对航天飞行器管路结构开展的失效分析多集中在管路结构自身的失效,但实际上,管路的焊接接头部位是管路结构的薄弱环节之一,在随机振动载荷下也容易发生疲劳失效。目前,多采用名义应力或者局部应力进行飞行器管路焊接结构的随机振动疲劳计算分析,但名义应力在复杂结构和工况上的应用存在局限性,而局部应力的计算精度严重依赖于有限元模型的网格尺寸,这些都会影响对焊接部位疲劳寿命的准确计算分析,并且大部分疲劳寿命分析未考虑到载荷、结构尺寸、材料属性等存在的离散性。
本文以航天飞行器复杂管路结构为研究对象,建立其有限元分析模型,并开展模态分析计算和模态试验验证该模型的有效性和准确性;继而采用结构应力法进行管路焊接结构的疲劳损伤分析,考虑焊接部位疲劳性能的离散性,推导给出结构疲劳寿命与可靠度之间的关系式;最终通过仿真分析获取管路焊接结构在随机振动载荷下的疲劳损伤以及疲劳寿命与可靠度的对应关系。
1 结构应力法
目前焊接结构疲劳分析方法主要有3 种——名义应力法、热点应力法以及结构应力法。名义应力是不考虑结构局部细节的整体应力,可以使用材料力学公式计算得到。焊接结构疲劳分析最初普遍使用名义应力法,但在实际工程中某些焊接接头形式难以明确地与特定接头类型对应,因此复杂结构的名义应力很难确定。热点应力法是在名义应力的基础上,通过平坦部位的名义应力外推得到结构的应力,可以使用通用的热点应力S-N 曲线来评估结构的疲劳寿命。该方法评估的准确性取决于外推点及外推方法的选取。结构应力法是董平沙教授针对焊接结构疲劳强度特殊性而提出的,通常是基于自由体的截面法,采用有限元输出的节点力和弯矩直接计算得到结构的应力。该方法具有网格不敏感的力学属性并且考虑了焊缝上应力集中的情况,因此分析结果的准确性高,于2007 年被美国机械工程师协会(ASME)标准收录作为三维焊缝疲劳寿命分析的方法。
为了下文更加方便地描述分析方法和有限元建模过程,简单介绍焊缝(即焊接件焊接后形成的结合部)的基本构成,如图1 和表1 所示。
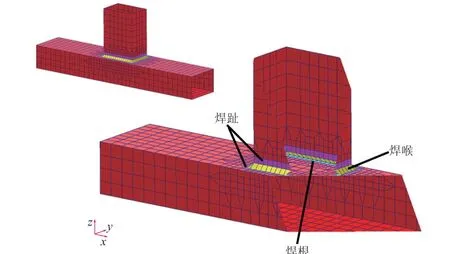
图1 典型焊接结构有限元模型Fig. 1 Finite element model of typical welded structure

表1 焊接部位构成说明Table 1 Descriptions of the welded positions
结构应力法基于力的平衡进行焊接部位应力的计算。焊缝截面上非线性分布的应力可以分解为2 部分——与外力相关的应力以及剩余的那部分应力。如图2 所示,第1 部分应力与外力相互平衡,称为结构应力;在结构处于受力平衡状态时,由于第1 部分应力已经与外力平衡,第2 部分应力虽然是高度非线性的,但处于自平衡状态,故称之为缺口应力。此时可以利用结构应力来表征焊缝处的应力分布,对焊缝的疲劳强度进行表征。
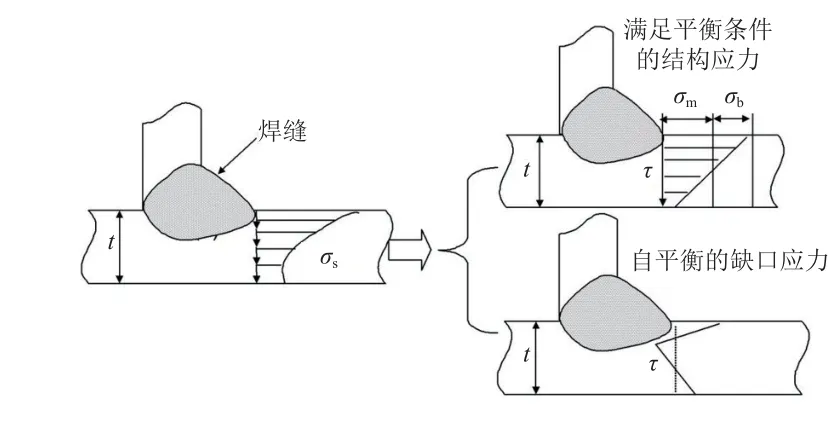
图2 焊接部位应力分布示意Fig. 2 Stress distributions in the welded part
结构应力法通过受力平衡推导焊接部位局部截面的受力状态,进而计算焊接部位的应力状态。焊接接头的截面受力包含拉伸的膜应力以及弯曲应力,两者之和与外力平衡。截面内均匀分布的膜应力为
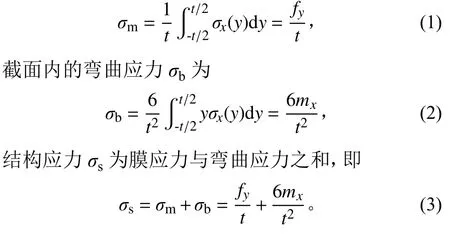
式(1)~式(3)中:f和m分别为线力和线矩,是指焊线单位长度上的力和力矩(焊线是为计算需要而自行定义的线,可以定义在焊缝里,也可以定义在热影响区域,通常定义在焊接结构的薄弱处,即焊趾上);为焊缝处的结构板厚。
焊接单元长度为,节点1、节点2 在轴方向的节点力及绕轴的力矩分别为F、F和M、M;轴方向单元边的线力及绕轴的线力矩分别为f、f和m、m,如图3 所示。
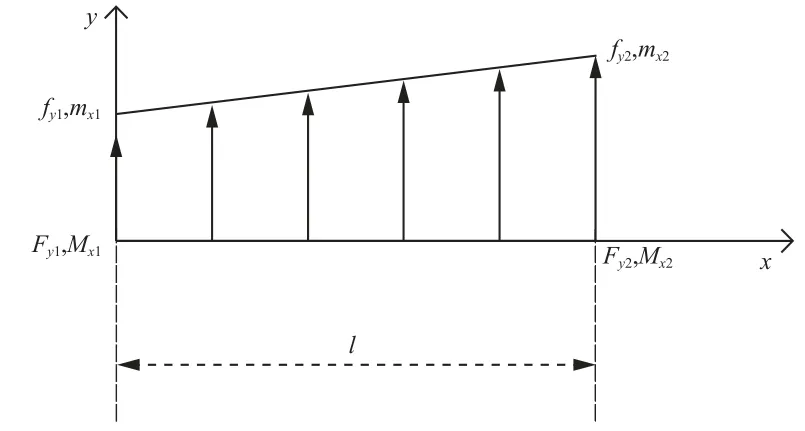
图3 两节点单元力及力矩分布Fig. 3 Distribution of force and torque in the two node element

通过结构应力计算式可以发现:力学特征完全由外载荷与接头本身的板厚控制。该公式是基于力平衡的概念提出的,且可以直接使用结构力学公式计算给出所在截面内沿着板厚方向的应力分布状态。进一步基于断裂力学理论,将结构应力转换为应力强度因子,采用统一的Paris 公式将短裂纹增长与长裂纹增长统一起来,并对时间进行积分,即可推导出焊接疲劳的计算式为

式中:和为试验常数;为疲劳寿命对应的应力循环次数;Δ为等效结构应力变化范围的数学表达式,主要与结构应力变化范围Δ、板厚、膜应力与弯曲应力状态有关。Δ的形式与材料S-N曲线相同,也称为主S-N 曲线,其有效性已经过专家学者以及权威机构的论证和试验验证,相关材料的主S-N 曲线及其试验数据已被收录于美国 ASME标准(2007)。
2 基于可靠度的疲劳损伤分析方法
2.1 焊接部位的P-S-N 曲线
在进行结构的可靠性分析时,需要考虑边界条件、材料属性及结构尺寸等的统计特性,才能确定结构在某一寿命条件下的可靠度。下面对考虑材料疲劳参数离散性的结构疲劳寿命计算方法进行推导。
考虑材料疲劳特性的离散性进行疲劳损伤分析时,需要使用材料的P-S-N 曲线。通常疲劳试验数据具有一定的分散性,而常规使用的S-N 曲线是通过统计处理后得到的材料疲劳特性中值曲线(每个应力量级下寿命取均值作为该应力下的寿命)。P-S-N 曲线则认为在某一应力水平下,材料疲劳寿命服从一定的分布。就机械结构的高周疲劳而言,应力水平一定的条件下,循环次数服从对数正态分布,其概率密度函数为
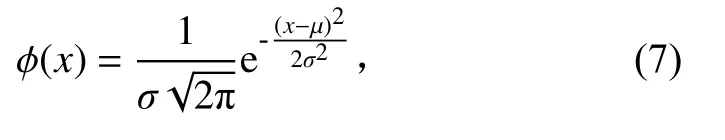
式中:=ln;为对数循环次数的均值;为对数循环次数的方差。变异系数的定义为=/。相关研究结果表明,不同应力水平下,循环次数的变异系数是相同的。在此基础上,设z为∈(0,1)标准正态分布的上分位点,即

式中:N为循环次数的均值;N表示在应力水平下可靠度为的循环次数。将N代入材料S-N 曲线中即可得到材料的P-S-N 曲线。
标准正态分布的上分位点代表使用疲劳寿命分析结果的可靠度,因此P-S-N 曲线是随着可靠度变化的一系列曲线簇。在疲劳分析过程中,根据寿命分配到的可靠度确定的数值,进一步确定疲劳分析过程中所用的S-N 曲线。利用该S-N 曲线计算得到的疲劳寿命的可靠度为。此时对比疲劳寿命的计算值和设计值即可确定疲劳寿命是否满足设计要求。
2.2 随机振动疲劳分析方法
结构随机振动疲劳分析方法可以分为频域法和时域法。随机振动疲劳频域分析方法中,结构的载荷是以功率谱密度函数(PSD)的形式给出的,结构的应力响应也是以频域计算方式获得(这里提到的应力是常规分析得到的应力,如主应力、Mises等,并非结构应力)。为了便于描述,首先给出应力PSD 谱的阶谱矩定义如下:
在平稳高斯随机过程中,结构的应力幅值服从一定的概率密度函数,其概率分布类型和概率密度函数的参数可以通过应力响应的PSD 谱计算得到,


传统的疲劳寿命分析中,根据载荷的带宽、结构的动力学特性等,应力幅值的概率密度函数()可采用Rayleigh 分布、Dirlik 分布、Zhao-Baker 分布等模型来描述,分布模型中的参数可以利用应力响应的各阶谱矩进行计算,这里不详细说明。
焊接疲劳分析所使用的结构应力是利用节点力计算得到的,在随机振动条件下,结构应力的统计分布特性与常规计算得到的应力有所差别。目前有模态结构应力、等效结构应力等方法用于在频域分析中描述结构应力的概率分布特性。
结构的时域损伤寿命分析过程中,载荷是以时间历程的形式给定的。通过结构动力学响应时域分析计算得到应力响应的时域历程,采用雨流计数法提取出结构应力响应的应力幅值和应力均值信息。由于平均应力对疲劳损伤有一定的影响,故需采用Goodman 平均应力修正等方法计算平均应力对损伤的影响。最后利用Miner 线性损伤累积准则计算结构的损伤寿命。
3 管路结构动力学分析模型
本文研究的对象是航天飞行器中的某空间管路结构,其中包含3 处焊接部位——细短管与其他部件连接处、细长管与薄壁圆筒连接处以及细长管与其他部件连接处。这3 处位置在图4 中以编号1、2、3 标识;管路部分采用壳单元进行建模,管接头部位施加固支约束。
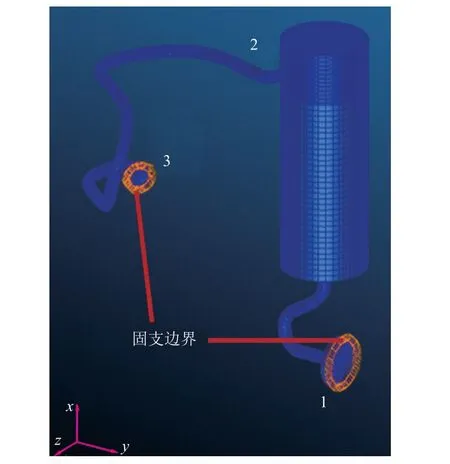
图4 空间管路结构示意Fig. 4 Schematic diagram of space pipeline structure

在管路结构的模态试验中,将包含管路的整体结构利用尼龙绳悬吊起来。此时管路处于真实的安装状态,整体结构的其他部件刚度远大于管路部分,模态测试过程中测量管路结构的局部模态。采用锤击法进行模态测试,利用Poleytec 扫描式激光测振仪进行加速度响应测量,可避免安装加速度传感器给结构带来的附加质量。模态试验采用多输入单输出方式,共布置7 个敲击点。模态试验测试系统及测点位置如图6 所示。
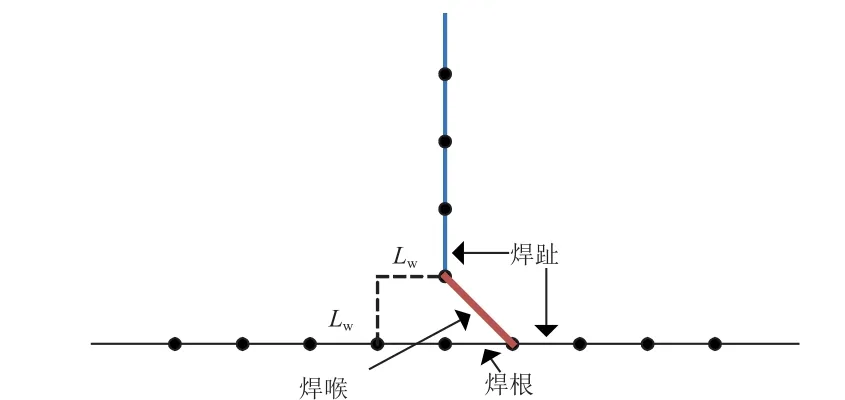
图5 焊接单元尺寸示意Fig. 5 The dimension of the welded unit

图6 模态试验测试系统及测点位置Fig. 6 Measuerment point positions in the modal test
管路结构模态振型和频率的仿真与试验结果对比如表2 和表3 所示。其中管路结构的第3 阶模态在试验测试中未能识别出,而观察仿真分析所得到的第3 阶模态振型可以发现,试验测点的位置没有明显的变化,可能是因为测点比较靠近模态节点,导致模态试验中未能很好地识别出。其他4 阶模态频率的仿真分析结果与试验测试结果间的偏差不超过3%,可以确定本文的管路结构动力学模型准确、有效。
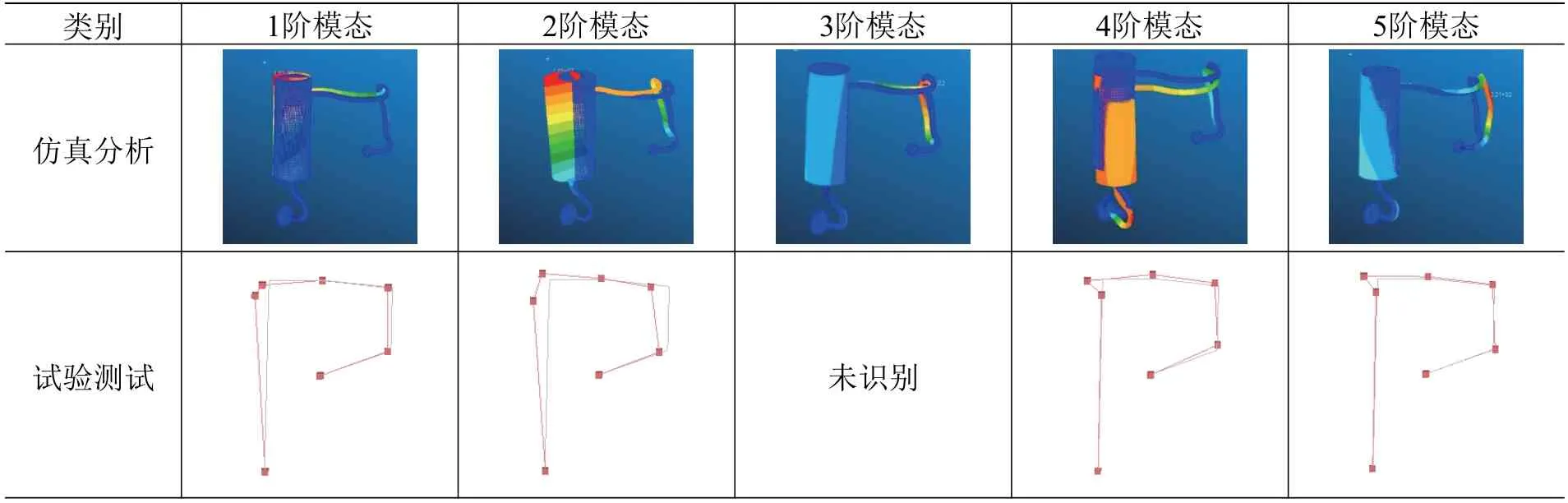
表2 仿真与试验的模态振型结果对比Table 2 Comparison of modal shapes between simulation and test results
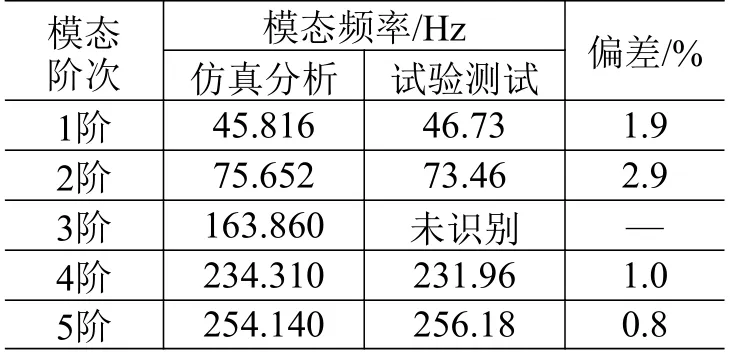
表3 仿真与试验的模态频率结果对比Table 3 Comparison of modal frequencies between simulation and test results
4 焊接结构疲劳损伤分析
采用时域分析方法开展焊接结构疲劳损伤分析,首先需要开展管路结构时域响应分析,获取焊接部位节点力的时域历程;然后利用节点力计算结构应力的时域历程;进一步对节点力进行雨流计数,获取结构应力的幅值和均值;最后结合主S-N 曲线进行焊接部位的损伤分析和疲劳寿命计算。
利用第3 章所建立的管路结构有限元模型开展随机振动响应仿真计算。本算例的随机振动载荷以加速度功率谱密度函数给出,谱密度为0.01/Hz,两侧上升段和下降段按照6 dB/oct 的速率变化,如图7 所示。利用加速度功率谱密度函数模拟出时间长度10 s 振动载荷的时域历程。管路连接的其他部件的刚度远大于管路结构的,根据模态试验仿真分析的结果,可以将加速度边界条件直接施加在管路两端被连接的部件上(模态分析中的固支边界处,参见图4)模拟基础激励状态。加速度时域历程如图8 所示。
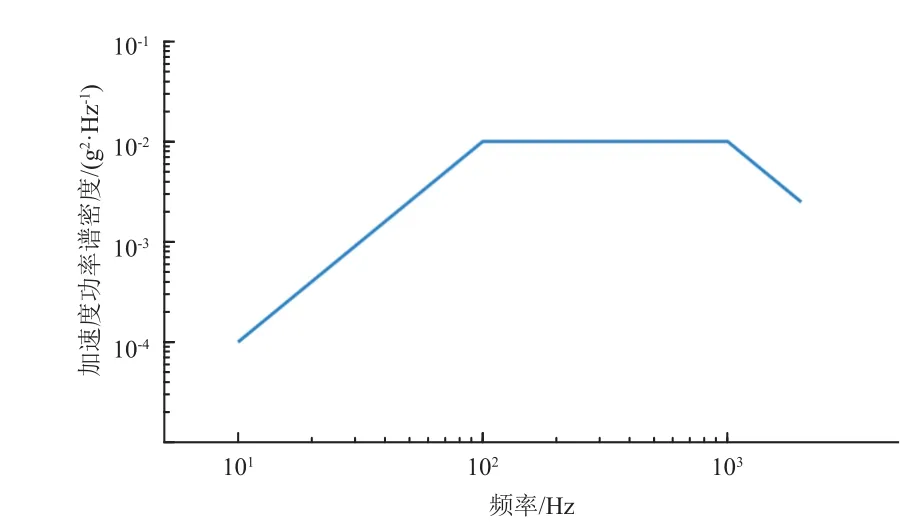
图7 随机振动加速度载荷谱Fig. 7 Spectrum of random vibration acceleration load

图8 加速度时域历程Fig. 8 Time domain history of the acceleration load
在完成管路结构随机振动响应的计算后,提取出焊接部位的节点力,利用商业有限元软件的后处理功能计算结构应力,并结合焊接材料的P-S-N 曲线进行焊接结构疲劳损伤分析。根据相关文献资料将钢材的中值主S-N 曲线参数选取为=19 930.2、=0.319 5,如图9 所示。在没有试验统计数据的情况下,对数ln所服从正态分布的方差设置为0.1。
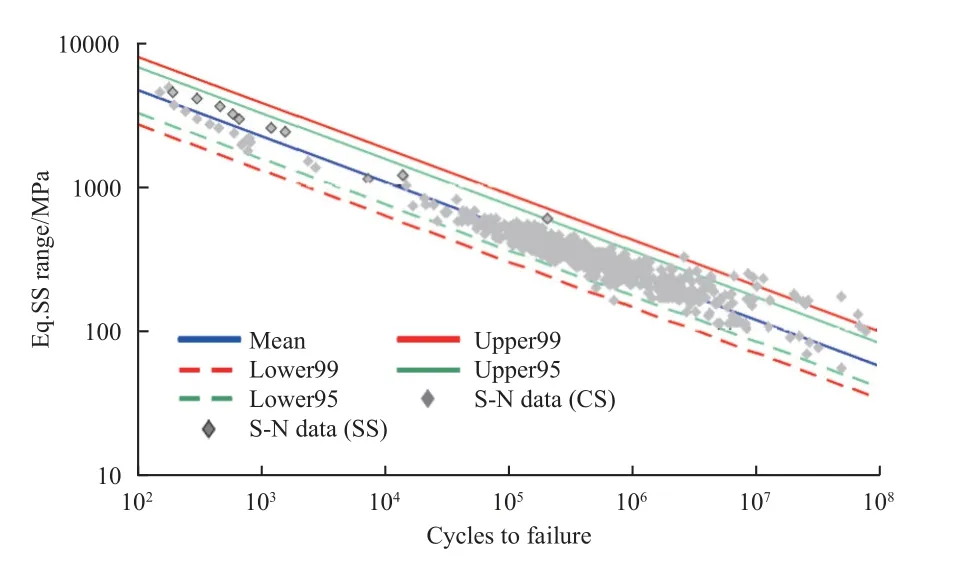
图9 钢材主S-N 曲线试验数据Fig. 9 Main S-N curve of test data of steel
通过分析计算,1 号焊接位置的损伤最大,管接头焊接部位的中位疲劳寿命为5.23×10s,局部的对数寿命云图如图10 所示。通过图10 可以发现,最大损伤位于焊趾处;焊喉处的损伤相对较小,不容易失效。管路结构在振动试验中的失效位置以及焊接部位的开裂位置与管路焊接结构的疲劳分析结果一致。

图10 焊接部位对数寿命云图Fig. 10 Nephogram of logarithmic life distributions at the welded positions
进一步,按照3的可靠度分布,计算不同可靠度条件下的管路结构使用寿命,结果如表4 所示。同时,通过拟合得到管路焊接结构使用寿命与可靠度的关系曲线如图11 所示,可以看到曲线呈指数函数形式。在管路结构可靠性分析过程中,可以根据管路结构的设计寿命确定此时管路结构的可靠度,也可以根据管路结构被分配的可靠度指标计算出相应的管路使用寿命,从而实现设计阶段按照使用寿命要求对结构的可靠度进行分配或者对薄弱部位进行改进加强。
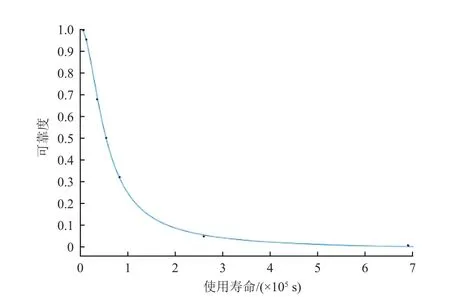
图11 管路焊接结构使用寿命-可靠度拟合曲线Fig. 11 Fitted curve of life time vs. reliability of the pipeline welded structure
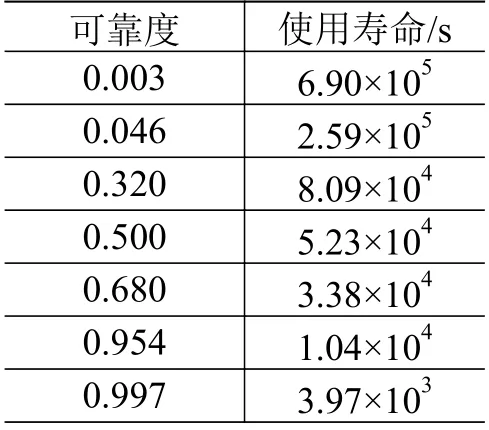
表4 管路焊接结构可靠度与使用寿命关系Table 4 Relationship between reliability and life time of the pipeline welded structure
5 结束语
本文采用焊接建模方法模拟焊接连接部位,采用壳单元模拟管路部分,建立复杂管路结构的动力学分析有限元模型。仿真分析与试验测试结果的对比表明,利用该方法建模得到的动力学分析模型前5 阶模态频率的偏差不超过3%。采用结构应力法对管路焊接结构疲劳寿命进行仿真分析,其结果可以有效预测管路结构的薄弱环节以及焊缝部位的开裂位置。在焊接疲劳分析中考虑材料特性离散性的影响,分析得到了管路结构使用寿命与可靠度之间的关系,为飞行器管路结构的可靠性设计分析提供了一条高效、可行的技术途径。
本文在损伤分析中仅考虑了材料疲劳特性的离散性对结构可靠度和使用寿命的影响,今后的研究中可以综合考虑载荷、边界条件、结构几何外形上的离散性,以更加全面地确定管路结构及其他类似结构使用寿命与可靠度的关系,为工程上管路结构的优化设计及可靠性分析等提供依据。
