基于模态试验和冲击响应试验的模型动力学参数修正

彭扬林，石 蒙，刘洪英，董 睿，韩 旭，赵亚雄，刘 磊，宫晓清

（中国航天员科研训练中心，北京 100094）

0 引言

航天产品的研制过程中，常用冲击响应谱动力学试验模拟航天发射过程的冲击动力学环境。而冲击响应数值仿真模拟可以辅助提升试验的验证效率，降低试验成本，指导冲击设备研发和试验调试。有研究人员对冲击响应谱的计算实施、不同参数下冲击响应谱计算值的变化规律等进行了研究，但是大多缺乏试验数据对比，无法评估仿真计算的准确性；又有研究人员针对试验验证和模型修正做了大量工作，但是对于阻尼修正的指导作用有限。冲击响应是一个复杂振荡的过程，要对其进行准确的数值模拟，需要对模型的动力学参数进行修正。

当前，针对冲击响应谱试验过程的动力学参数修正的研究相对较少。本文拟基于模态试验和冲击响应试验过程，对数值计算模型动力学参数进行修正，模态试验过程修正弹性模量、泊松比和厚度参数，冲击响应试验过程修正阻尼参数，旨在提高冲击响应谱预测精度。

1 模态试验及参数修正

1.1 模态试验实施

模态试验采用东方振动和噪声技术研究所的INV3062T 型信号采集分析仪，结合力锤和力传感器实施。被测的响应板为500 mm×400 mm×10 mm的铝合金平板，其四角通过螺栓安装固定。模态试验过程采用多点激励单点响应的方式，根据平板尺寸按照100 mm 的间隔设置激励点，激励点编号按从左至右、从下至上的顺序编为1～30，原点导纳（响应传感器）位于激励点16，如图1 所示。试验时，分别对激励点1～30 进行敲击，采集各点的激励力和加速度响应信号，得到响应板的各阶模态固有频率。

图1 模态试验响应板上的激励点及其编号Fig. 1 Excitation points and their numbers on the response plate of modal test

1.2 模态参数修正

建立响应板的有限元模型如图2 所示，对其四角的螺栓安装孔进行固定约束，然后计算结构的固有频率，响应板的材料参数为弹性模量71 GPa、泊松比0.33。

图2 响应板的有限元模型Fig. 2 Finite element model of the response plate

以试验测试得到的固有频率（见表1）为优化目标，以响应板的弹性模量、泊松比和厚度为优化参数，基于响应面优化的方法进行优化计算。

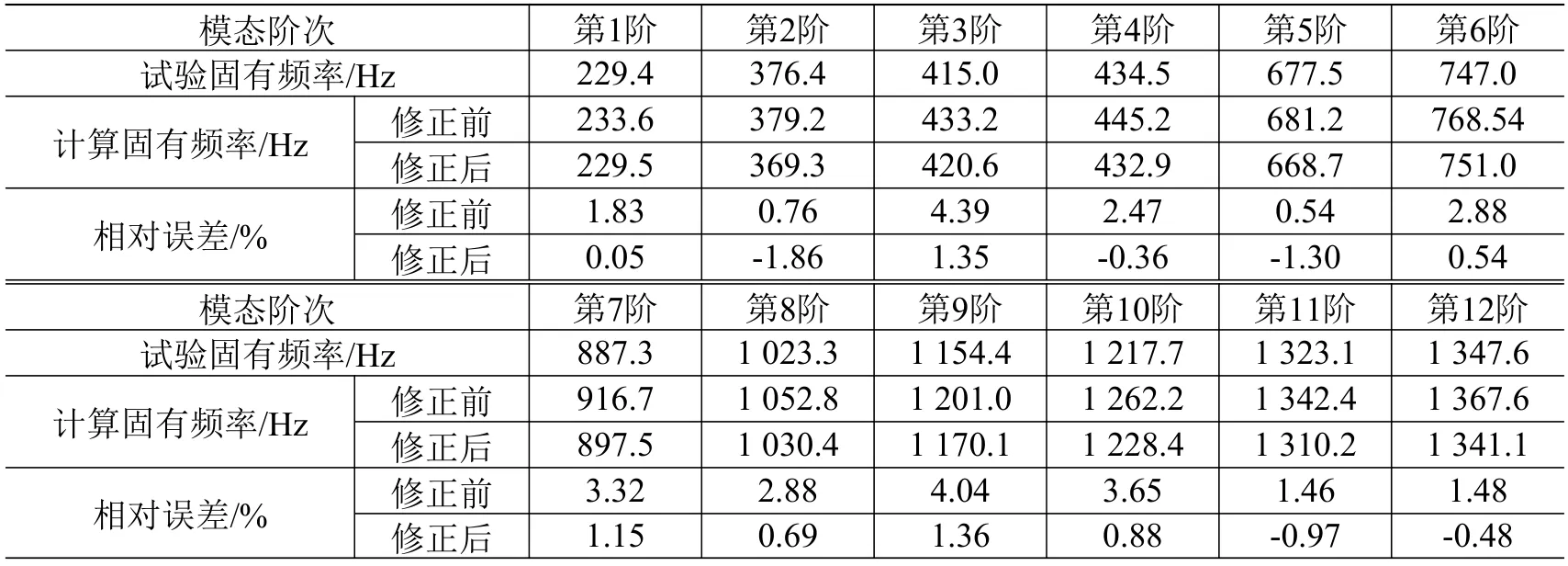
表1 参数修正前/后的响应板固有频率Table 1 Natural frequency of response plate before and after parameter modification

多项式型响应面是常用的响应面类型，对于二次多项式响应面，可表示为

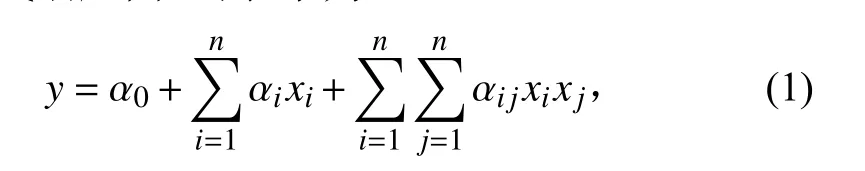
式中：为响应面；为输入变量；、α、α为回归系数。由于采样点数量通常大于多项式的项数，所以式(1)为超定方程，无法得到精确解，常用最小二乘法拟合求得其近似解。得到的最优参数为：弹性模量66.927 GPa，泊松比0.3625，厚度9.9956 mm。

参数修正前/后的响应板前12 阶模态固有频率值如表1 所示。经过参数修正后，前12 阶模态固有频率计算值的相对误差大部分较修正前有所降低，均在±2%内，说明基于模态测试的动力学参数修正有效。后续冲击响应谱数值仿真过程，采用修正后的弹性模量、泊松比和厚度值进行计算。

2 冲击响应谱试验及参数修正

2.1 冲击响应谱试验实施

响应板及冲击响应的测量点位置如图3 所示。冲头提高到设定高度后，经过自由落体过程与响应板发生碰撞，通过加速度传感器采集响应点的时域数据并根据Runge-Kutta 算法，在品质因子=10、分析频率间隔为(1/6)oct 条件下，进行冲击响应谱的计算。

图3 冲击响应测试的测量点位置Fig. 3 Positions of measuring points on the response plate for shock response test

冲击高度为6.3 cm 的条件下，响应点1 和点2 的冲击时域曲线和响应谱曲线如图4 和图5 所示。

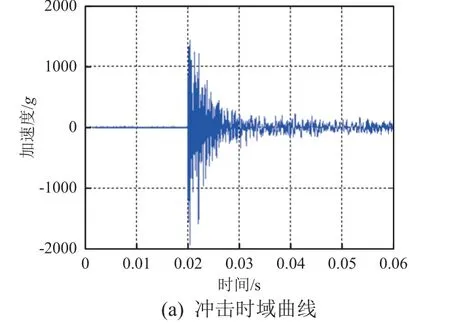
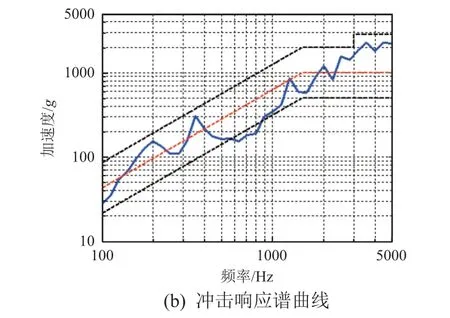
图4 响应点1 的冲击响应曲线Fig. 4 Shock response curve at point 1

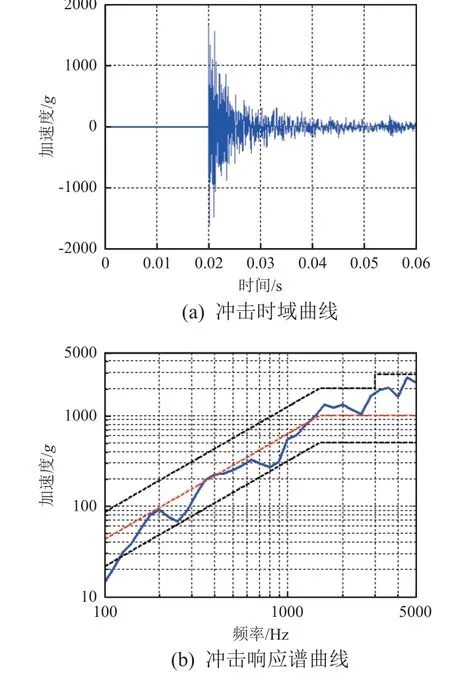
图5 响应点2 的冲击响应曲线Fig. 5 Shock response curve at point 2

2.2 冲击响应谱数值仿真

以图2 所示的有限元模型进行数值仿真，响应板上的4 个安装点固定约束，冲头赋予按冲击高度换算的自由落体速度；冲头和响应板发生碰撞冲击，提取传感器响应测量点的加速度时域响应数据，采用与2.1 节冲击响应谱试验相同的计算参数，得到冲击响应的数值计算结果。

数值计算的阻尼采用Rayleigh 阻尼，通过质量阻尼系数和刚度阻尼系数来模拟冲击响应过程的振动衰减。为了评估数值计算和冲击试验过程的响应差异程度，计算在频率间隔为(1/6)oct 条件下，数值计算和试验过程的冲击响应谱曲线各分析频率点的均方根误差

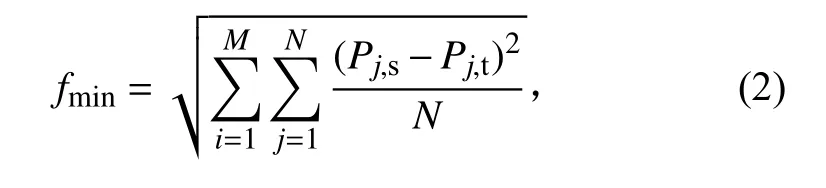
式中：为评价使用的响应点序号，为响应点数量，本文=2；为分析频率点的序号，为分析点数量，本文=35；P和P分别为数值计算冲击响应谱曲线和试验冲击响应谱曲线上第个分析点的加速度值。评价目标越小，则认为数值计算得到的响应和试验响应间的差异越小。

2.3 阻尼系数修正

Rayleigh 阻尼和各阶模态阻尼比的关系可以表示为

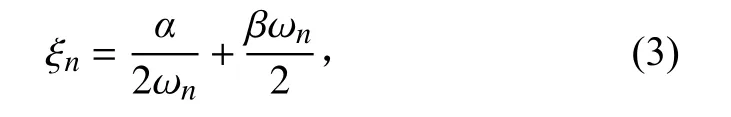
式中：ξ为第阶模态阻尼比；为质量阻尼系数；为刚度阻尼系数；ω为第阶模态的固有频率。该冲击响应谱的计算频率范围为100～5000 Hz，在该范围内结构的最小和最大固有频率分别为229 Hz和4987 Hz。假设各阶模态的阻尼比均为0.03 时，代入式(3)可以计算得到：=82.7，=1.83×10。

为了找到最优的阻尼系数，对如表2 所示的参数进行全因子实验的数值仿真计算，并与图4 和图5 的试验冲击响应谱曲线对比进行均方根误差计算。得到质量阻尼系数、刚度阻尼系数和均方根误差值的关系如图6 所示的标记点。对所有标记点进行曲面拟合，得到曲面上最低点的质量阻尼系数、刚度阻尼系数和均方根误差值分别为113.88、1.75×10和438.01。

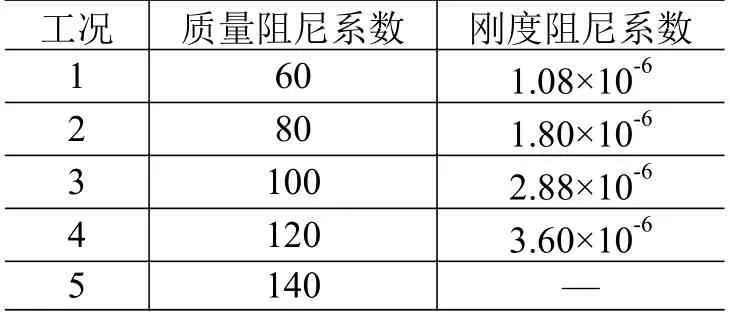
表2 全因子实验参数Table 2 Parameters of the full factorial experiment

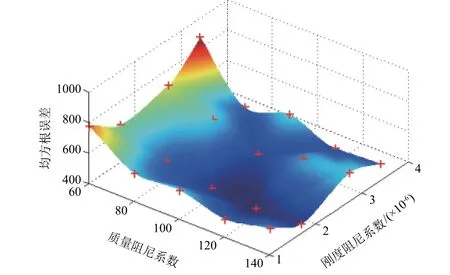
图6 阻尼系数和均方根误差的关系Fig. 6 Relationship between damping coefficients and root mean square error

3 试验验证

在基于模态试验修正的弹性模量、泊松比和厚度值，以及基于冲击响应试验修正的质量阻尼系数、刚度阻尼系数条件下，对冲击高度为3.3 cm、9.3 cm、12.3 cm 的冲击工况进行验证。相关工况的参数见表3。

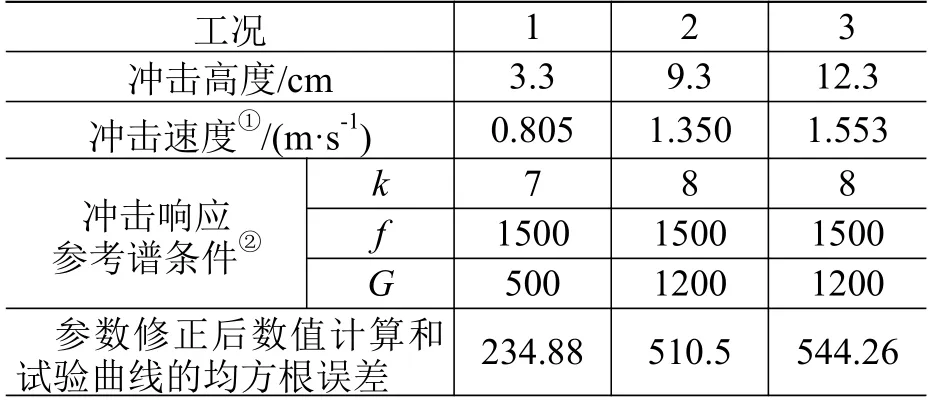
表3 试验验证的不同工况Table 3 Different working conditions in verification test

3 个工况对应的修正前/后数值计算以及冲击试验2 个响应点的响应曲线对比如图7～图9 所示。可以看到，响应板上2 个响应点的修正后数值计算曲线与试验响应曲线均吻合较好，大部分频率段的误差在±6 dB 以内，较修正前的数值计算结果误差明显减小。这说明通过动力学参数修正，数值计算模型能够较好地模拟该响应板的冲击响应。

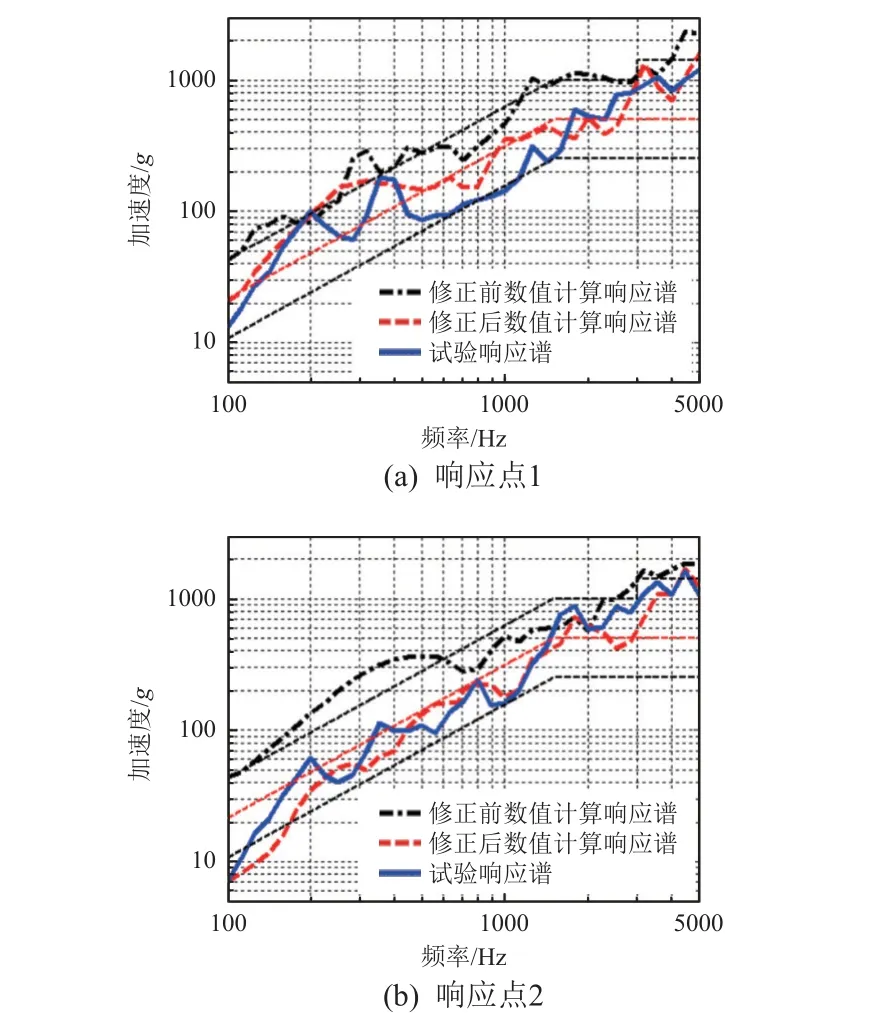
图7 工况1 的计算及试验冲击响应谱Fig. 7 Calculated and tested shock response spectrums under working condition 1

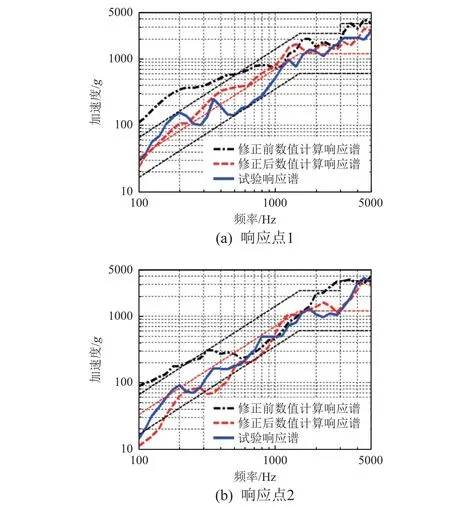
图8 工况2 的计算及试验冲击响应谱Fig. 8 Calculated and tested shock response spectrums under working condition 2

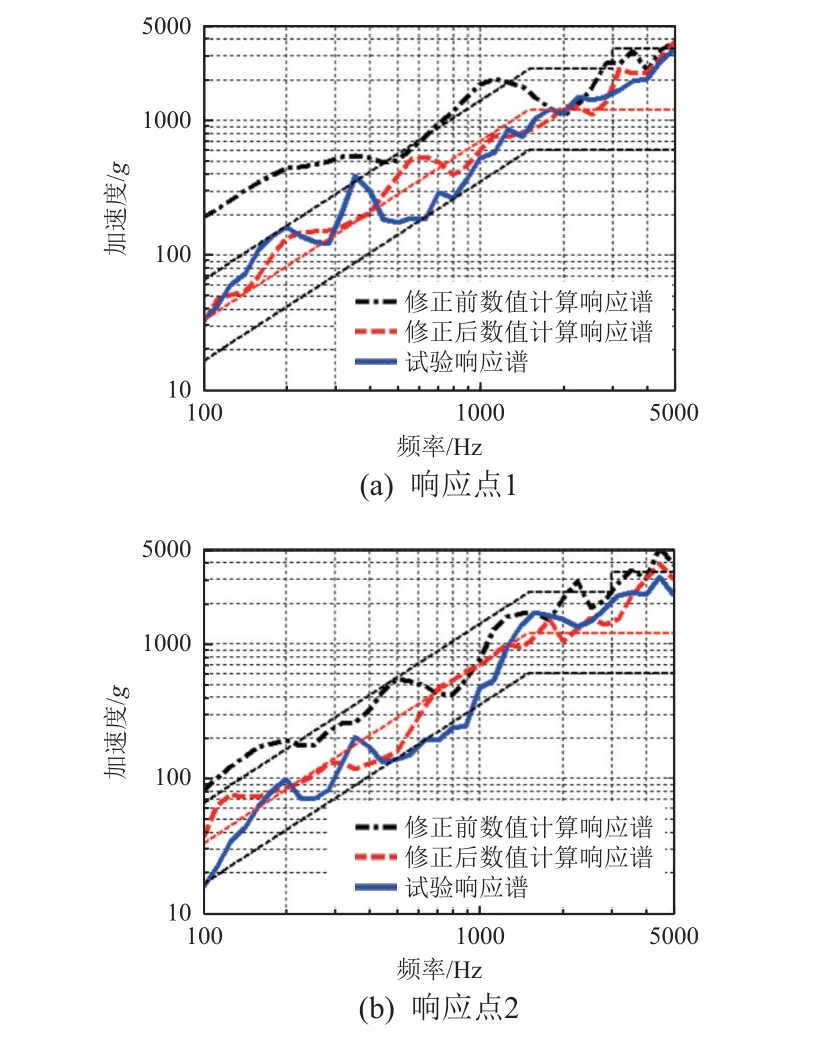
图9 工况3 的计算及试验冲击响应谱Fig. 9 Calculated and tested shock response spectrums under working condition 3

4 结束语

分别通过模态试验和冲击响应试验对响应板结构的模型动力学参数进行修正。修正后，结构的固有频率误差在±2%以内；模型在预测冲击高度为3.3 cm、9.3 cm、12.3 cm 工况下的冲击响应过程中取得较好的预示效果，大部分频率段的误差在±6 dB 以内。可见，动力学参数修正后的数值计算模型有效提高了预测精度，对于实际工程中的设备研制以及冲击响应谱试验规范调试具有一定的指导作用。