STEAM教育理念下高中数学主题式教学策略

唐海军 胡蓉 刘双 王佳佳 陈芳芳

摘      要 为了提高教育质量，需要优化教学方式，探索基于学科的课程综合化教学。在中学数学课程中实施主题式的教学，需要从STEAM教育理念入手，通过分析数学主题式教学的内涵与特征，以及数学课程标准与教科书中存在的主题，提出主题式教学策略。

关 键 词 STEAM教育理念  高中数学  学科整合  主题式教学

引用格式 唐海军，胡蓉，刘双，等.STEAM教育理念下高中数学主题式教学策略[J].教学与管理，2022（12）：94-98.

在技术创新日新月异和全球化面临挑战的时代，科学、技术、工程、艺术和数学（STEAM）综合能力的培养变得非常重要[1]，是提高公民的个人学科素养，增强国际竞争力，成为负责任的公民的重要基础。然而，最新的国际学生评估结果显示，即使在欧洲、美国和澳大利亚等经济发达的国家，也有大约20%的学生缺乏足够的数学或科学技能。这一趋势突显出STEAM教育方面迫切需要采取行动，实现STEAM教育与学科教育的融合。以数学学科为例，虽然人们普遍认为数学是所有其他STEAM学科的基础，但STEAM教育的理念对于数学学科自身的教学，对于培养学生的数学核心素养到底有何启发，却鲜有论述。因此，从跨学科的STEAM教育视角审视数学的主题式教学活动具有重要价值。

一、STEAM教育理念概述

STEAM教育是指解决问题时借鉴数学和科学的概念和程序，结合工程的团队合作和设计方法，并使用适当的技术，融合人文艺术内容的教育形式[2]。STEAM教育作为一种跨学科教育形式，其核心价值在于教育要基于问题情境，引导学生突破学科的谷仓效应，在多学科融合、多活动支撑、多模态交互中培育学生问题解决能力、沟通协作能力以及探究创新的素养。

STEAM教育的核心理念影响着教师如何在学校分科课程中利用STEAM教育的优势，做到学科的取长补短，促进学生学科核心素养的发展。首先，从概念上和本质上讲，STEAM是跨学科的。这种跨学科性质可以概念化为“一种将个别学科联系起来的整合方法，从而使学习变得相互联系、集中、有意义，并与学习者相关”[3]。STEAM教育的关键是以数学为基础，通过工程和艺术来解读科学和技术。其次，从活动方式看，高质量的STEAM活动都有三个必要的成分：一定有问题要解决;活动一定涉及重要的数学问题;问题解决需要团队合作与利用多个学科的知识和方法[4]。G·Yakma指出高质量的STEAM教育应是立足于实际问题，学生通过协作和实践完成项目与问题解决，从而提升综合素养和问题解决能力[5]。最后，从学科融合看，Lyn D.English立足于21世纪技能，认为学校教育不仅需要确保数学在STEAM环境中得到应有的重视，而且需要为学生提供平等的机会来发展数学素养，以便成功参与当前和未来的世界发展。鉴于能力的培养，Lyn D.English提出了一些促进跨学科的问题解决的建议，包括通过产生有创意的问题来确定内容和过程的目标，促进对内容的深入理解，发展一般技能和过程，以及培养跨学科建模能力[6]。

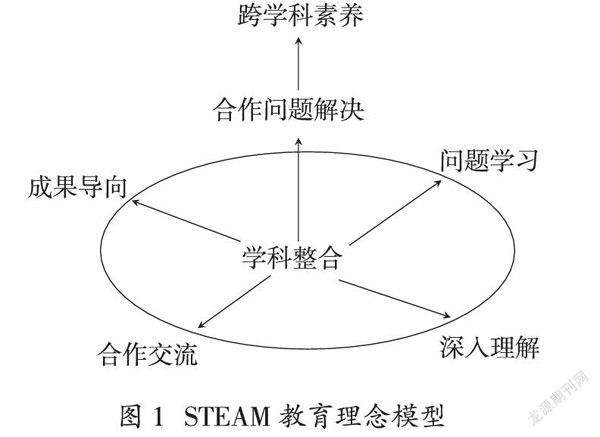
由此，可以认为STEAM教育的核心理念是以学习者为中心，学科整合为基础，指向合作问题解决，进而培育学习者的跨学科素养。跨学科素养被视为学习者在学科素养的基础上形成的、超越特定领域、综合运用所学知识和思想方法解决问题所表现出来的必备品格和关键能力。这一核心理念对于学生的学科学习与课堂教学而言，是通过聚焦问题学习、深入理解、合作交互和成果导向四维度来实践的（如图1）。

图1  STEAM教育理念模型

学科整合表现在教育理念上应倡导学习者跨学科学习概念，注重学习与现实世界的相互联系;培养学习者综合素养技能与认知，强调学习者的主动探索及创新精神。问题学习，即立足于项目或问题的解决。通过解决问题的方式学习，是人类学习的源动力，比如最早的人类为解决生存问题采用了播种和驯养牲畜，以确保食物的本地化供应并导致了农业的发端[7]。深入理解，是對STEAM教育中指向的问题进行深度分析，在不同学科知识与方法之间寻找联系，对其解决方案富有想象力的探求。深入理解项目所涉及的基本原理和概念，与其内容和背景无关。合作交互，即STEAM的教育是以团体为教学对象，协作探究、沟通表达，在认知与社会互动中完成课程的学习。问题解决与协作交流是培养学生理解数学过程和解决问题的过程性标准之一。成果导向，即解决问题获得一个相对于学习者而言的创新成品，这个成品可以是实物，如机器人、3D打印产品、科技论文、问题解决方案等。对于数学学科而言，学习是以融会贯通的建模形式，将碎片化的工程技术、材料科学、艺术创造情境知识结合起来，制定出可操作性的问题解决方案。

二、高中数学主题式教学特征与主题

1.数学主题式教学的特征

数学主题式教学是指在教师的干预指导下，学生围绕某一个或一系列具有挑战性的学习主题，开展自主思考、合作探究、解决问题的一种教学形式。主题式教学表现出以下的特征：从教学方式看，围绕一个主题采用项目活动式、问题解决式、启发探究式实施;从教学内容看，聚焦于某一个微型的话题，或一系列的同一主题持续进行;从思维角度看，主题式教学需要学生的高阶思维参与（如创造性思维、批判性思维、元认知与问题解决）。具有跨学科情境的主题无疑适合高中阶段开展主题式教学，因为这样的主题具有学科整合特性，能够极大地满足主题式教学的特征，使得参与者更方便地感悟到数学可以影响和促进对其他学科基本思想与概念的理解，同时其他学科的渗透也能给予高中生数学学习更多的启示。如及时地认识到数学与科学、工程、技术与艺术之间的双向联系;认识到技术在制作与使用辅助工具的过程中推动着数学学习;艺术对于数学而言，不再局限于数学的美学范畴，是培育数学创造力的关键抓手。

2.数学课程与教材中的跨学科整合主题

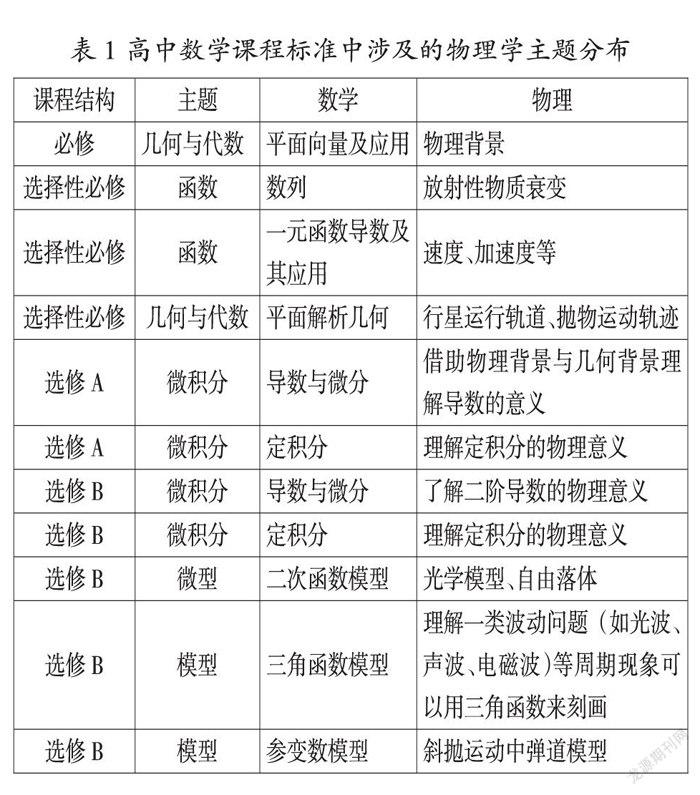
反映STEAM教育理念的学科整合教学在美国比其他国家更为普遍，并在该国得到了大力提倡。STEAM学科之间的联系已经在2000年《学校数学的原则和标准》中进行了描述，其中要求学生解决在数学和其他环境中出现的问题。2010年的《共同核心国家标准》证实了这一觀点，并建议数学课程应让学生为解决日常生活、社会和工作中出现的问题做好准备。近年来，由于对STEAM学科重要性的认识提高，人们也将重点放在改善分离学科的教学上，尤其是科学和数学学科。STEAM学科融合的理念同样也在我国高中数学课程改革中体现出来。《普通高中数学课程标准（2017年版）》提出高中数学课程的设置旨在为学生的可持续发展和终身学习创造条件，课程内容具有基础性、选择性和发展性的特征，因此，在数学课程标准的内容中也已经体现出跨学科融合现象，比如与物理学的联系，相关主题分布见表1。

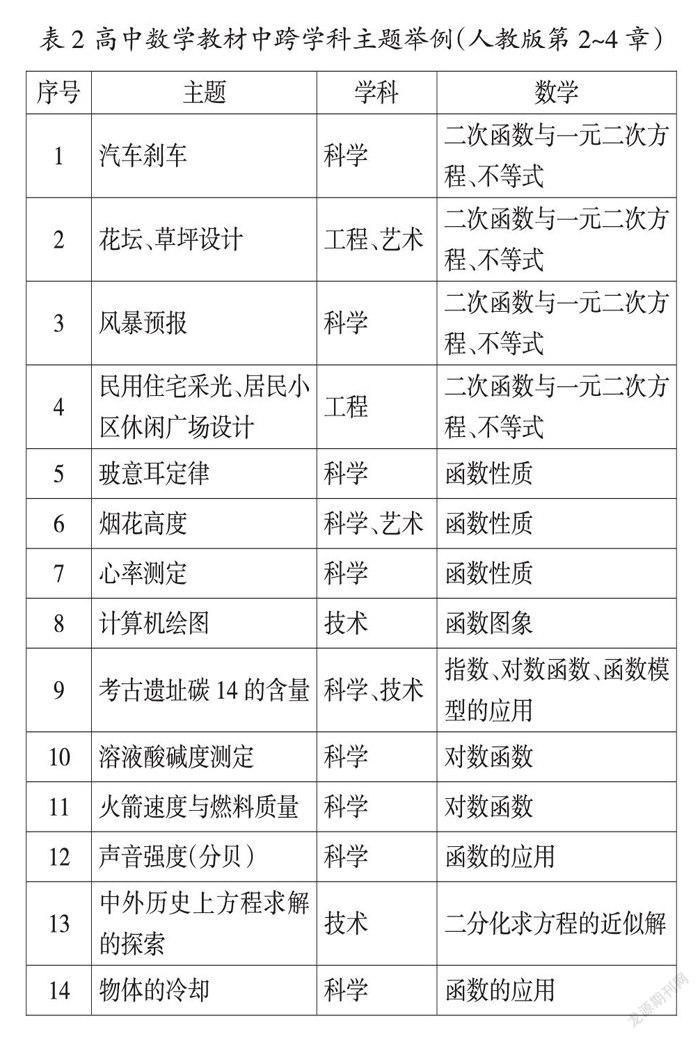
由表1可以看出，《普通高中数学课程标准（2017年版）》中在必修和选修系列课程中也提出了较多的与物理学主题相关的情境要求。比如，在选择性必修中，建议将一元函数导数及其应用与物理情境结合起来开展教学，引导学生经历一个由平均变化率过渡到瞬时变化率的过程，从而更好地与大学数学内容衔接。为了贯彻数学课程标准的要求，出版社在教科书编写上也呈现出学科整合的导向，例如高中数学人教版教科书（2019版）必修第一册中的“函数”主题就有较多的科学、工程与技术主题，为数学教师实施跨学科主题教学提供了丰富的素材（见表2）。

三、STEAM教育理念融入数学主题式教学的策略

学校数学教学的一个重要目标是使学生能够模拟、处理和提炼超出他们所学范围的问题，帮助他们组织和整合数学思维。为加深学生对数学的认知，培育学生数学建模素养，以及增强其问题解决能力和跨学科素养，教师应从STEAM教育理念入手，围绕数学中存在的跨学科主题，通过确定主题、深度理解、合作指导与成果产出开展主题式的教学活动。

1.确定适应问题的主题

虽然不是所有的数学内容都应该通过问题解决来教授，但设计一个对学生认知要求有一定挑战性的跨学科主题，以及非结构化的问题，有助于培养高中生有效问题解决能力与数学应用意识，这将是关系主题式教学有意义实施的前提。对于如何确定一个适应性的主题，可以从以下这些方面着手。

（1）立足学生主体地位

在跨学科的主题下，学生问题解决就不是简单地获得数学结果，而是应该鼓励学生发展一种更富有成效的数学方式来思考给定的综合情境，经历解决问题的过程或生成问题解决的策略。把学生放在学习的中心，鼓励他们提供、设计、参与有意义且有挑战性的主题情境，可以积累更高层次的认知推理经验。

（2）借鉴国外经验

在国际上，跨学科主题在有关国家的数学课程标准中早已有融合的尝试。法国《高中数学大纲》明确指出要将数学与物理等学科联系起来，并强调教学内容与实际应用相互联系，通过学生的探究来发现大千世界的奥妙。例如让学生构造矩形板上的气缸来探究头发衍射的厚度，可通过测量来培养学生的动手能力和分析数据的能力，并把统计与物理联系起来，而在思考如何确定头发直径的近似范围时，又把线性函数与物理联系起来[8]。

（3）挖掘数学教材

在国内的人教B版2019年高中数学教科书必修第二册“4.1.2指数函数的性质与图象”的情境与问题中出现的“碳14问题”，就是一个能够引发学生想法和挑战欲望的主题。从STEAM视角，围绕放射性物质衰变这一科学主题，教师在课后组织学生经历科学的探究过程，设计一系列的科学探究主题和问题串，碳14是什么？碳14方法的起源、用途是什么？碳14与我们的函数学习有什么关系？你们能够将放射性物质的衰变模型建构出来吗？这不但加深学生对指数函数和对数函数模型的理解，而且通过科学事实培养学生的科学与人文素养。

2.促进对内容的深入理解

在确定了创意问题之后，就需要对主题采取深度的学习，对问题与学科知识、跨学科联系有更深刻的理解。虽然工作和生活中出现的许多问题只需要基础数学，但重要的是，这些知识需要更为流利地涌现、使用和应用[9]。这就需要学生丰富对代数、几何、统计学和数据分析等主题的深入理解，并培养他们将这些理解应用于各种数学和真实问题的技能。

（1）深入理解基本原理和概念

在数学的跨学科主题学习中，重要的是深入理解基本原理和概念，需要学生先认识到这一主题内的问题有待学习的必要性。例如，在初中学生已经学习了二次函数，为什么高中还要学习二次函数与一元二次方程、不等式。教材上更多地是从数学内部去体现，如要求二次函数的最值、要为后面学习函数的单调性做铺垫。如果教师能够结合实际生活场景，引导学生把二次函数作为一种数学模型，在刻画现实世界的最优化方面有着广泛地应用，例如工程视角、花坛喷水池的设计、商品销售等。比如学校商店的松饼销售问题[10]，卖松饼活动给学生们介绍了二次函数，并描述了在这种情况下使用函数的方式，为复习以前遇到的函数词汇（如系数、变量和指数）提供了机会。学生不仅可以利用相关的情境来应用和模拟二次函数，而且用二次方程和函数来决定卖松饼的定价和策略，以获取销售的最大利益。

（2）重建数学概念与应用

实施数学的跨学科主题教学，需要学生具备概括深层概念知识的能力，能够从数学联系的思想对数学概念与应用的本质进行再加工。比如“对数”内容，课标要求学生理解对数的概念和运算性质，知道用换底公式能将一般对数转化成自然对数或常用对数等知识目标。教师使用人教A版教科书必修第一册中的习题4.4“声强级问题”这一主题，有助于学生思考为什么需要学习对数，为什么要学习10底的常用对数。声强级L（单位分贝，dB）与声强I（单位：瓦/米2）的函数关系满足L=10lg（I/10-12）。

然而，声强级与声强为什么是一种以常用对数表示的函数关系？为什么要用声强级而不是声强表示声音的响度？这就需要教师有意识指导学生跨学科去思考解决这些疑问。在物理学中，描述声音强弱的客观物理量是声强，能够引起人的听觉的最低声强是10-12瓦/米2。实验研究表明，人的听觉对声音强弱的感觉是基本符合对数规律，与声强的对数成正比的，即客观声强增大10倍，人的主观感觉是增大1倍;客观声强增大100倍，人的主观感觉只增大2倍……因此，为了简便计算就用对数函数模型建立了“声强级”的概念。教科书中是直接呈现声强级的对数公式，若教师能引导学生课后去查询和学习声学相关资料，则有助于他们进一步理解对数的运算原理，体会“对数”源于生活中大数运算的准确度、速度的提升和计算方法的改进等现实需要。

3.实施合作问题解决的指导

（1）教师干预指导的必要性

在过去的几十年里，无论是在课程内还是在课程之外，合作解决问题的一般技能和过程受到了广泛的关注。在工作场所，成功的工程师或技术人员使用数学来更好地理解其所处的工作系统，比如在野外安装通讯基站的工程人员，必须要考虑到信號覆盖面更广和便于操作维护等因素来确定最佳的安装地点。为解决现实问题，他们相互协商，用数学知识来化解难题。而在学校，教师在主题式教学中起到关键作用。当学生理解主题之后，尝试解决问题时不可避免存在各样的困难，教师通过安排学生像成人那样合作解决问题、社会化学习、交流与沟通、批判与质疑、探索与反复。这也是回应我国《普通高中数学课程标准（2017年版）》中提及的中学生通过自主探索、合作研究来论证数学结论与解决问题的要求。

（2）教师干预指导的步骤

学生参与主题式学习可能会遇到错误，遇到小组的认知冲突、人际冲突，遇到观点的分歧和争议。如人教B版高中数学必修5.2“探究活动：由编号样本估计总数及其模拟”。生活中，为了便于管理，人们经常会对人或物进行连续编号。“编号问题”在实际的科学、工程情境中是有战略意义的。不同学生根据生活经验，对“编号”活动与相应数学知识也就有了不同层次的理解。教师教学首先需要学生清楚活动的目标、规则;再安排学生与其他同学分工合作，寻找生活中有连续编号的实例，获取适当容量的编号样本，讨论估计总数的多种方法;最后，小组需要将探究活动填写在教科书所提供的记录表上。在此过程中，教师要深入到小组观察与干预指导，即时评估指导效果与主题教学的效果。设计与组织实施合作解决问题的教学强调的是培养学生“带走的能力”，而不是“背不动的书包”，这也是STEAM教育的意义之所在。

4.形成多样的学习成果形态

STEAM教育理念之一是跨学科的应用，这种应用呈现出可视化成果产出的特征。STEAM教育活动的成果更多是“物化”的，如智能机器人、设计的产品。然而对于STEAM教育理念视角下的数学学习而言，主题学习成果的反应更要聚焦在数学的学科特点上。

（1）学生获得跨学科解决问题的思想

学习者能够应用相互渗透的视角看待诸多领域，而不是水果拼盘式的聚合，如认识到数学与艺术有交集，艺术与数学能够融合在一起，二者在人类思维上是互为补充的。

（2）学生能够用数学模型表征问题

现行的中学数学课程及教科书中也将数学建模素养作为培育核心素养的一个重要维度。其中，函数模型是应用最广泛的数学模型之一。很多的实际问题一旦被识别为函数关系，就可以通过研究函数的性质，利用函数模型解决问题。比如高中人教B版中编排的用分段函数描述阶梯水价、阶梯电价制度;用二次函数建模寻找最佳的苹果出售时间点。

（3）学生能提出解决问题的优化方案

北师大版初中9年级教科书中，通过要求学生比较哪一个梯子更陡的活动，引入锐角三角函数中正切知识的学习。教学中借助不同的楼梯情境，学生小组经历观察、思考、交流、猜测、验证等探究环节。虽然从数学学习的角度，学生可以认识到正切被用于刻画楼梯的坡度或陡度，但从STEAM这种视角来看，楼梯模型可与高中的斜率、斜面、重力和做功等静力学知识联系起来，也可以利用变化率来理解工程环境中坡度和陡度的概念。在这种情况下，与变化率相关的正切、斜率等知识对于理解楼梯结构、道路结构和车辆安全下坡等工程问题至关重要，从而使得学生认识到函数是优化设计、刻画现实世界极为重要的工具。

总之，融入STEAM教育理念对数学教学提出了许多挑战，但将当前的教育范式转变为STEAM教育视角，在数学教学中嵌入学科整合的实践活动，包括基于问题的学习、基于项目的学习、科学探究和工程设计，是最有可能增强学生认识校外世界运作方式，并帮助学生发展以明智的方式应对社会变化和挑战的知识和能力。

参考文献

[1] Katja Maass etc.The Role of Mathematics in interdisciplinary STEM education[J].ZDM，2019，51：869-884.

[2][4] J.Michael Shaughnessy.Mathematics in a STEM Context[J].Mathematics Teaching in the Middle School，2013，18（06）：324.

[3] JKP Smith.The Interdisciplinary Curriculum：A Literary Review and a Manual for Administrators and Teachers[J].Administrator Guides， 2000：24.

[5]Yakman G.STΣ@ M Education：an overview of creating a model of integrative education [J].Pupils Attitudes Towards Technology 2006 Annual Proceedings， 2008， 341-342.

[6] English Lyn D.Advancing Mathematics Education Research Within a STEM Environment[C].//In K.Makar et al.eds.），Research in Mathematics Education in Australasia 2012-2015，DOI 10.1007/978-9

81-10-1419-2_17

[7] 伯尼·特里林，查尔斯·菲德尔. 21世纪技能——为我们所生存的时代而学习[M].天津：天津社会科学出版社，2011：84-88.

[8] 史宁中，孔凡哲. 十二个国家普通高中数学课程标准国际比较研究[M].长沙：湖南教育出版社，2013：144-146.

[9] English，L.D.，& Gainsburg，J.Problem-solving in a 21st-century mathematics Curriculum[C].//In L.D.English & D.Kirshner（Eds.）， Handbook of international research in mathematics education （3rd ed）. New York：Taylor & Francis.2016：313-335

[10] Partnership for 21st Century Skills.Framework for 21st Century Learning Definitions.Partnership for 21st Century Skills[EB/OL].（2019-4-20）[2020-6-26].http：//static.battelleforkids.org/documents/

p21/P21_Framework_DefinitionsBFK.pdf

[作者：唐海军（1982-），男，四川南充人，四川文理学院数学学院，副教授，贵州师范大学数学科学学院，博士生;胡蓉（1985-），女，四川南充人，四川文理学院数学学院，副教授，硕士;刘双（1990-），女，四川达州人，四川文理学院数学学院，助教，硕士;王佳佳（1993-），女，四川达州人，四川文理学院数学学院，助教，硕士;陈芳芳（1989-），女，四川达州人，四川文理学院数学学院，助教，硕士。]

【责任编辑  郭振玲】