配电网中储能电站的经济性分析
2022-05-08唐海燕王德君钱喜鹤缪月森李妍妍
唐海燕,王德君,钱喜鹤,缪月森,李妍妍
(杭州市电力设计院有限公司余杭分公司,浙江 杭州 310030)
引言
近年来社会高速发展,电力需求上升,季节性用电高峰给配电网的规划运行以及电力调度带来巨大挑战[1-3]。将储能装置引入配电网可以有效解决上述问题。
储能电站具有多重作用,对于电网来说,可以减缓相关设备的扩建,降低成本。对于用户侧来说,可以对负荷削峰填谷,降低需求量[4]。目前国内外学者已经对储能系统进行了充分研究,但缺乏储能电站应用于配电网时的经济性研究。因此,本文以储能电站年均收益为目标函数,在传统储能系统经济效益的基础上,考虑储能电站建设在配电网时对发电侧、电网侧、用户侧等多方面效益,结合放电深度与电池寿命的关系,把总投资成本根据实际运行的放电深度折算为年均投资成本,对其经济性进行研究。
1 配电网中储能电站的效益分析
1.1 电价效益
为了解决负荷峰谷差过大,提出了分时电价的概念,并在波谷时段降低电价刺激用户的用电积极性。储能电站可以在电价高时段放电,并在电价低时段充电。依靠电价差来获取经济效益,降低购电成本。
1.2 减缓电网容量扩建
随着负荷增加,当符合大于线路的容量时,需要对输电线路进行扩建。在一些配电网扩建可行性较低、负荷高峰持续时间较短的地区,储能电站可以代替传统电网的扩建升级。
2 储能电站经济效益分析模型
2.1 储能电池的数学模型
储能电池数学模型包括:一是储能电池的寿命模型。二是储能电池的建设以及运维的成本模型。
2.1.1 储能电池的寿命模型
储能电池的寿命S 计算模型如式(1):
式中:Mi,R是电池在放电深度R 第i 次循环充放电时对电池寿命的损耗。储能电池的等效充放电系数如式(2):

式中:Ni是第i 次充放电时折算到满充满放状态的最大循环次数;N0是电池满充满放的最大循环次数,取值范围[0,1];Mi表示为:

当充放电深度为R 时,量化后的电池循环次数如式(4)[4]:

式中:α1、α2、α3、α4、α5是由电池寿命测试数据回归模拟获得的一组常数。
2.1.2 储能电池的成本模型
储能电池的成本模型如式(5),(6):
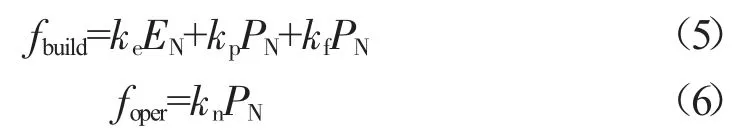
式中:ke、kp、kf、kn分别为储能电池单位容量成本、储能电池单位功率成本、储能电池其他辅助设备的单位功率成本;EN为储能电池的额定容量;PN为储能电池的额定功率;T 为储能电站的全寿命运行时间。
2.2 储能电站经济效益分析模型
2.2.1 目标函数
以储能电站运行的总收益作为目标函数,模型表达式如式(7):
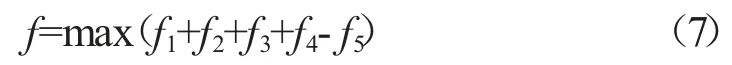
式中:f1为峰谷电价产生的收益;f2为减缓电网扩建的收益;f3为发电侧的收益;f4为政府补贴;f5为储能电站投资运维成本。
2.2.2 约束条件
1)储能充放电功率约束。储能电站的充放电速率不超过限值,且不能同时充放电。
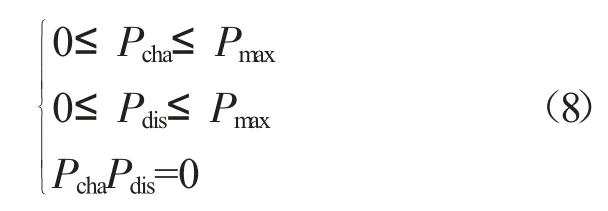
式中:Pcha,Pdis分别为储能电站的充放电功率;Pmax为储能电站的最大充放电功率。一天中储能的充放电量应平衡。

2)荷电状态约束。储能的荷电状态不超过限值。
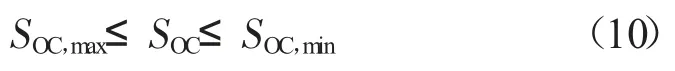
式中:SOC,min,SOC,max为储能最大最小荷电状态。
3 模型求解
储能电站经济性分析流程图如图1。
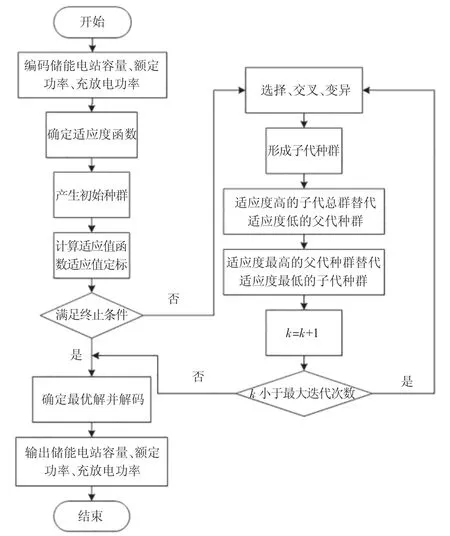
图1 含精英保留策略的标准遗传算法流程图
装置折旧率取0.03;配电装置单位造价为100万元/MW;年利率为0.07;发电设备扩建单位容量成本为210 万元/MW;储能的充放电效率为85%。
4 算例分析
4.1 算例相关参数
本文选取某地区典型日负荷进行算例分析,绘制该地区的峰谷电价如图2 所示。具体步骤如下。

图2 分时电价
1)据储能电池的寿命模型计算出放电深度与最大充放电次数的关系。
2)忽略电池寿命的影响进行求解,得出每天根据负荷进行削峰填谷的充放电次数。
3)计及电池寿命进行求解。
基于含精英保留策略的标准遗传算法求解模型,得到配电网储能电站的最优容量和功率,验证所提方法的可行性与有效性。
4.2 算例结果分析
通过储能寿命计算方法得出的充放电次数与放电深度的关系如表1 所示。
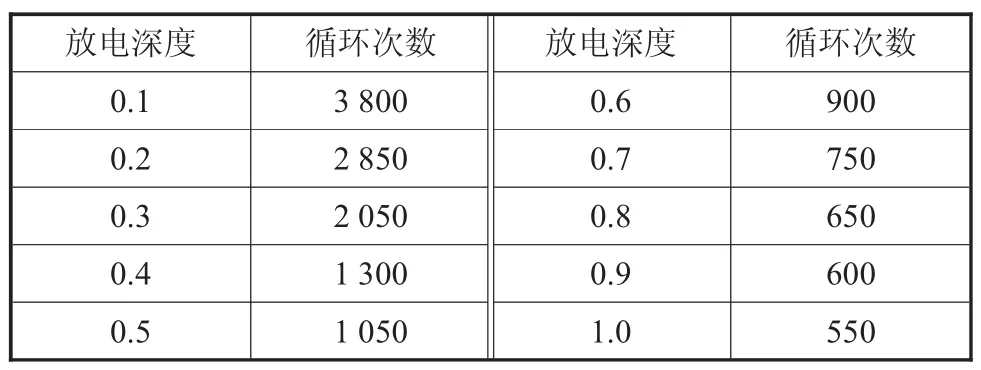
表1 储能充放电次数与放电深度的关系
通过以上数据进行模型求解,得到储能电站收益的收敛特性如图3。
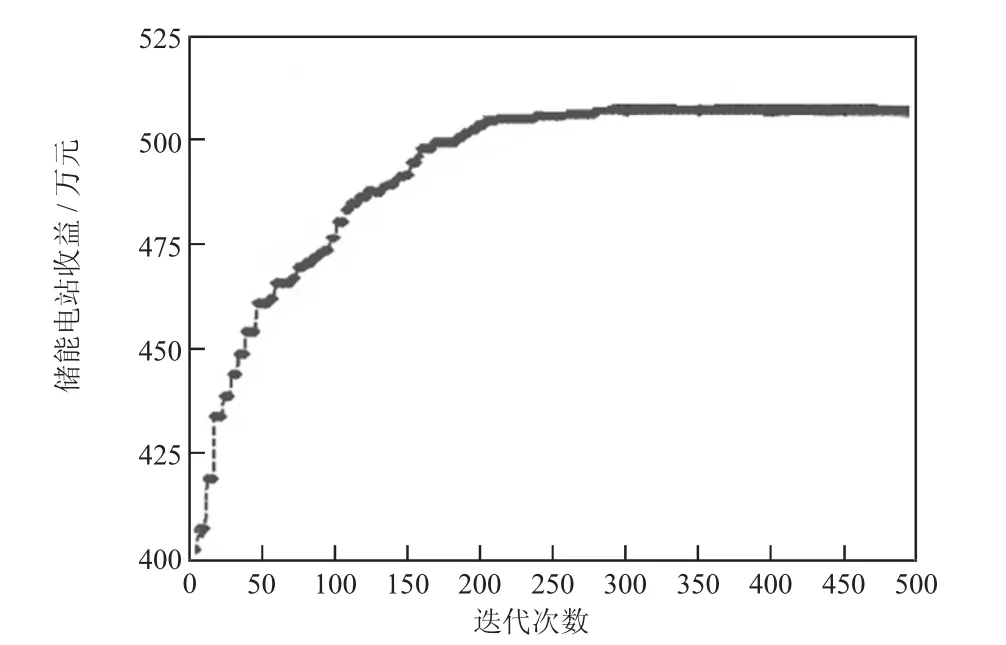
图3 储能电站收益收敛特性
绘制储能充放电效率与收益的曲线图如图4。证明提升储能电站性能参数可以提高储能系统的经济性。
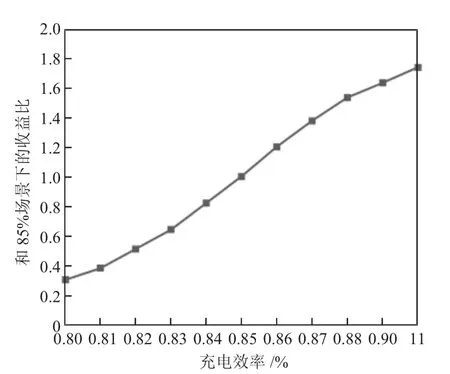
图4 不同充放电效率下的经济性曲线
5 结论
1)在配电网建立储能电站,存在经济效益,年均回报率为9.98%,使用10 年即可回收成本。
2)电池性能对储能电站的经济性影响较大,与经济效益呈正相关。
3)电池寿命受放电深度影响,且经济效益最大化时,电池放电深度会使电池寿命维持在较高水平,减少年均建设成本。
