基于区间值中智软集合的突发事件下弹性供应商选择方法研究★
2022-05-08张国业侯晨静董媛香
张国业,侯晨静,董媛香
(1.山西省数字政府服务中心,山西 太原 030031;2.太原工业学院经济与管理系,山西 太原 030013;3.太原理工大学经济管理学院,山西 太原 030024)
引言
新型冠状病毒肺炎(COVID-19)疫情的突然爆发和蔓延,迫使人员隔离和交通运输阻隔,全球大量企业停工停产对供应链造成了极大威胁。在全球经济一体化的背景下,供应链呈现相互依存且利益关系错综复杂的网状结构,企业为应对激烈的国际竞争,常常采用准时生产方式(JIT)及供应商管理库存(VMI)等供应链管理模式,当面对疫情等破坏性大且损失规模难以控制的突发事件时,任何一个供应商的阻断都会对整个供应链网络造成不可逆转的威胁。
因此在突发事件背景下,选择一个更有弹性的供应商,可以在供应链受到扰动或中断后迅速恢复其原始或达到更佳状态[1]。弹性供应商本质是具备比竞争对手更好地应对风险和意外事件的能力[2]。然而,突发事件的低概率和高强度特征决定了突发事件下弹性供应商选择具有高度不确定性,也使得该决策问题更加复杂[3]。一些学者采用随机模型来研究不确定环境下的弹性供应商选择问题,使用最广泛的方法是两阶段随机规划模型[4]和双目标规划模型[1,5]。然而,随机模型在处理大量属性数据和群体决策过程中模糊性方面没有优势。因此,另外一些学者利用模糊集及其扩展方法探讨不确定环境下的弹性供应商选择问题。其中,模糊集和TOPSIS 结合的方法引起广泛关注[3-6]。
虽然基于模糊集的决策方法在弹性供应商选择中具有良好的应用效果,但模糊集与概率论、粗糙集和区间数学理论均存在参数化不足的缺陷,因此Molodtsov[7]提出了软集合理论解决这一问题。此外,软集合还具有对数据类型没有限制且可以直接建立近似模型快速求解的优势。目前,软集合已被成功应用到数据挖掘[8]、组合预测[9]和决策问题[10]等方面;相关理论也得快速发展,逐步扩展到模糊软集合[11]、次协调软集合[12]和中智软集合[13]等各种类型的软集合。其中,中智软集合可以表示数据的隶属度、不确定度和非隶属度,进一步扩大了不确定数据的描述范围,可以解决包含冲突信息的复杂不确定问题。考虑到在不确定环境下,用区间值代替精确值来处理隶属度更实用,Deli[14]进一步提出了区间中智软集合的概念。
综上,本文考虑到突发事件背景下的高度不确定性,以及决策信息存在冲突等复杂情况,采用可以表示不确定性和冲突性的区间值中智软集合作为弹性供应商选择的基本方法,并提出区间值中智软集合的确定程度、冲突程度以及邻近度测度概念及方法。基于邻近度、熵权法和组合赋权的思想分别测度专家权重,参数客观权重和参数综合权重。最后,考虑到专家决策的心理因素,结合前景理论(Prospect Theory)构建了基于区间值中智软集合的突发事件下弹性供应商选择群决策模型,并通过实例验证该方法的可行性。
1 预备知识
定义1[15]令U 为初始论域,u 为论域U 中的任意元素,定义在论域U 上的区间值中智集A={<u,TA(u),IA(u),FA(u)>,u∈U}(T,I,F:U→[0,1])包含元素u 对于区间值中智集A 的隶属度TA(u),不确定程度IA(u)和非隶属度FA(u)。其中,TA(u)=[infTA(u),supTA(u)],IA(u)=[infIA(u),supIA(u)],FA(u)=[infFA(u),supFA(u)]。且对于∀u∈U,均满足0≤supTA(u)+supIA(u)+supFA(u)≤3。
为方便起见,我们用A(u)=<[infTA(u),supTA(u)],[infIA(u),supIA(u)],[infFA(u),supFA(u)]>表示元素u对于区间中智集A 的隶属程度,并称A(u)为一个区间值中智数。
定义2[14]令U 为初始论域,E 为参数集。设P(U)为论域U 上所有区间值中智集的集合,称(F,E)为论域U 上的一个区间值中智软集合,当且仅当F 是E 到P(U)所有子集的一个映射,记作F∶E→P(U)。
定义3[16]区间值中智数A(u1)和A(u2)间的标准化汉明距离为:

2 区间值中智软集合相关运算
2.1 确定程度和冲突程度测度
定义4 令min=<[1,1],[0,0],[0,0]>为最小冲突区间值中智数,表示对象对于集合的隶属度为1,不确定程度和非隶属度均为0,即信息冲突程度最小。
定义5 令max=<[0.5,0.5],[1,1],[0.5,0.5]>为最大冲突区间值中智数,此时隶属度和非隶属度均为0.5,不确定度为1,即信息冲突程度最大。
定义6 设A(u)=<TA(u),IA(u),FA(u)>为一个区间值中智数,其中TA(u)=[infTA(u),supTA(u)],IA(u)=[infIA(u),supIA(u)],FA(u)=[infFA(u),supFA(u)],则A(u)的确定程度定义为:
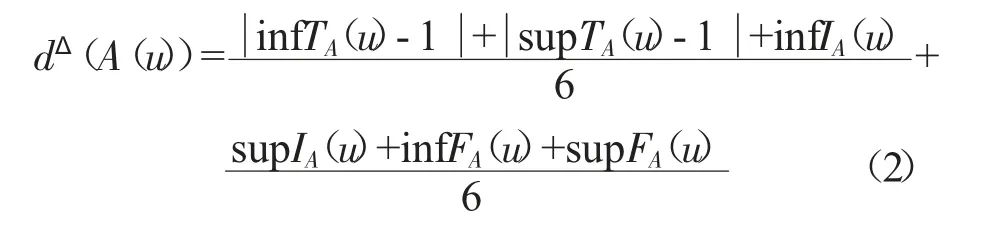
可知,确定程度衡量的是区间值中智数A(u)与最小冲突区间值中智数min 之间的标准化汉明距离。中智数A(u)与min 之间的距离越小,确定程度越大;反之,确定程度越小。类似地,将区间值中智数A(u)与max 之间的标准化汉明距离衡量A(u)的冲突程度。
定义7 设A(u)=<TA(u),IA(u),FA(u)>为一个区间值中智数,其中TA(u)=[infTA(u),supTA(u)],IA(u)=[infIA(u),supIA(u)],FA(u)=[infFA(u),supFA(u)],则A(u)的冲突程度定义为:

可知,区间值中智数A(u)与max 之间的距离越小,冲突程度越大;反之,冲突程度越小。
2.2 邻近度测度
定义8 假定集合U={u1,u2,...,ui,...,um}为论域,E={e1,e2,...,ej,...,en}为参数集,(F,E)和(G,E)为论域U 上的两个区间值中智软集合。
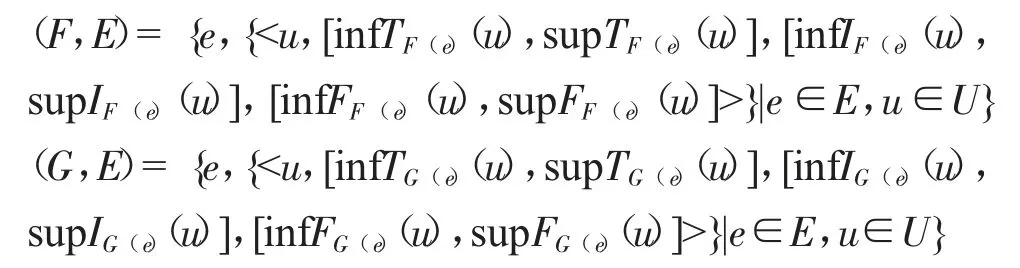
则(F,E)和(G,E)之间的邻近度测度为:
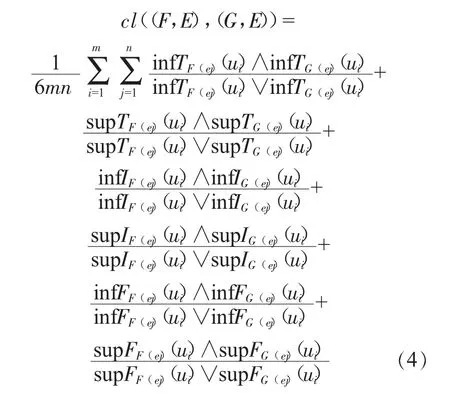
其中,∧表示两者之间取最小值;∨表示两者之间取最大值;且cl((F,E),(G,E))∈[0,1],当cl((F,E),(G,E))越接近于0 时,表明区间值中智软集合(F,E)和(G,E))之间的邻近度越低;反之,邻近度越高。
3 突发事件下弹性供应商选择的群决策方法
3.1 问题描述
设U={u1,u2,...,ui,...,um}为候选供应商集,E={e1,e2,...,ej,...,en}为供应商弹性参数集,R={r1,r2,...,rl,...,rz}表示专家集,z 个专家分别给出评估弹性供应商的区间值中智软集合为(Fl,E)(l=1,2,...,z),用区间中智数=<FFl(ej)(ui),IFl(ej)(ui),FFl(ej)(ui)>(i=1,2,...,m;j=1,2,...,n;l=1,2,...,z) 表示专家rl对备选弹性供应商ui关于某个弹性指标参数ej的评价值。其中,TFl(ej)(ui)=[infTFl(ej)(ui),supTFl(ej)(ui)],IFl(ej)(ui)=[infIFl(ej)(ui),supIFl(ej)(ui)],FFl(ej)(ui)=[infFFl(ej)(ui),supFFl(ej)(ui)]。
3.2 决策过程
3.2.1 专家权重的确定
本文基于邻近度思想构建专家权重模型。
首先,构建z 个专家rl对候选供应商弹性指标评价值的区间值中智软集合(Fl,E)(l=1,2,...,z)。
其次,计算各个专家给出的供应商弹性指标评价值均值的区间值中智软集合,则有:
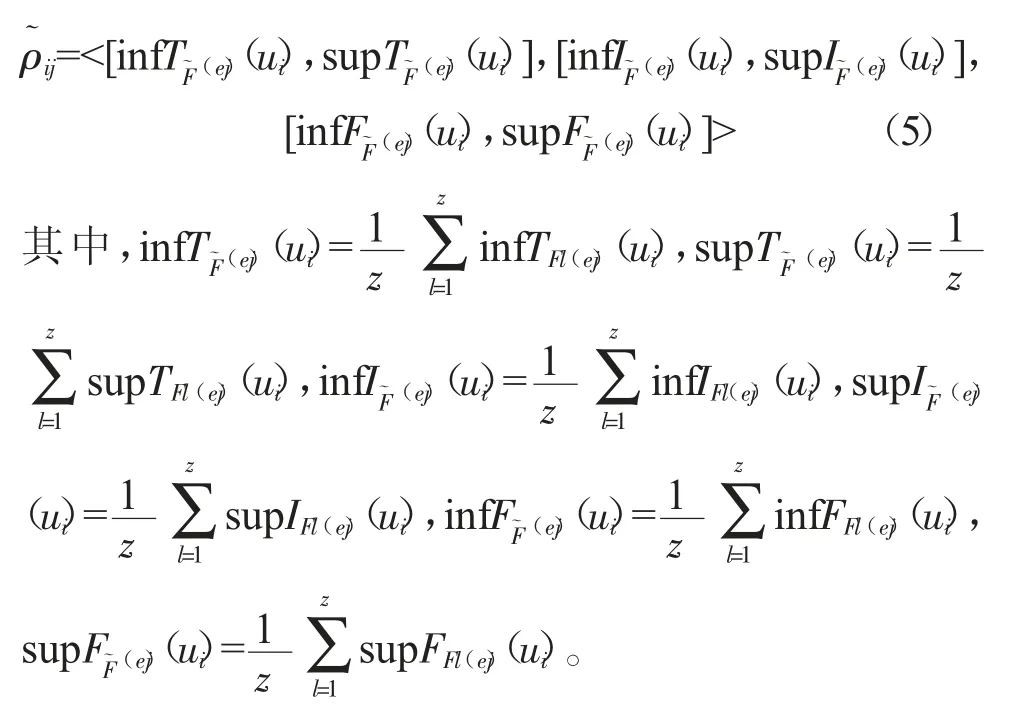
在此基础上,依据公式(4),测度区间值中智软集合(Fl,E)(l=1,2,...,z)与之间的邻近度,邻近度越高,专家权重越大。
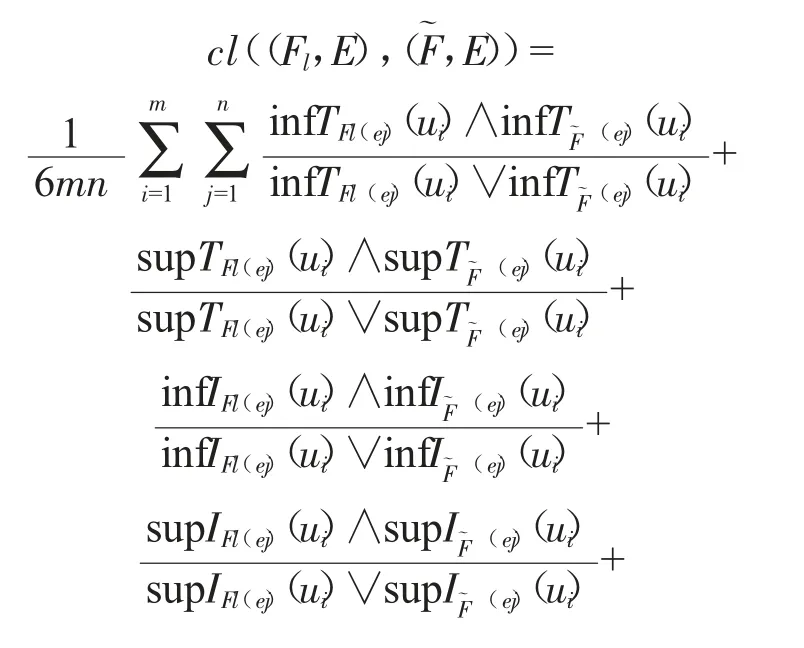
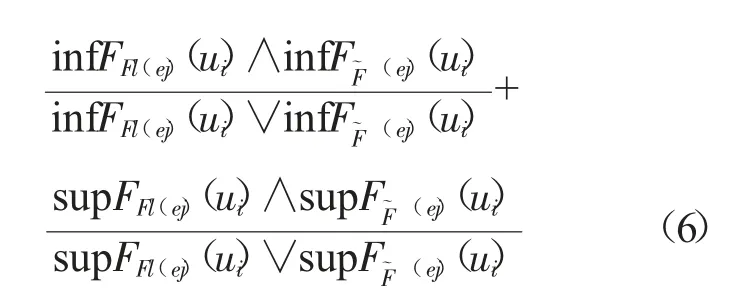
最后,计算专家权向量φ={φ1,φ2,...,φl,...,φz}。其中,
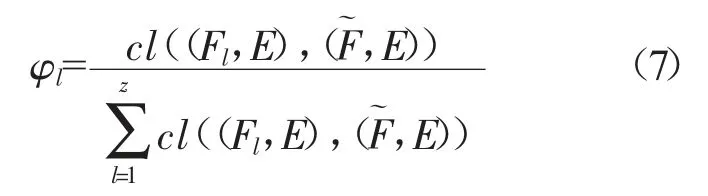
3.2.2 参数综合权重的确定
3.2.2.1 参数客观权重计算
当属性值不相等且权重未知时,利用熵测度可以确定属性的客观权重,信息熵越小则各供应商之间该弹性指标差异越大,权重越大。本文采用基于信息熵的客观赋权法——熵权法[17],可推断专家rl(l=1,2,...,z)给出的区间中智软集合(Fl,E)中参数ej(j=1,2,...,n)的熵值为:
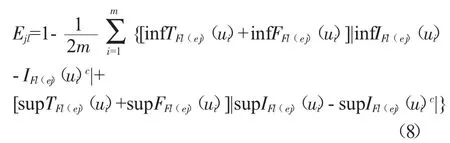
则参数ej的熵值为:
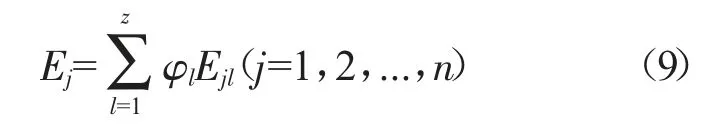
其中,φl表示专家的权重。
故参数ej的客观权重值为:
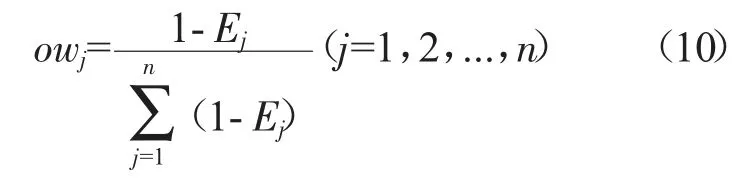
3.2.2.2 参数综合权重值计算
本文采用组合赋权的方式,基于最小信息熵原理将主观权重和客观权重结合得到参数综合权重。这里假定参数的主观权重直接由专家给定,令参数主观权向量为SW={sw1,sw2,...,swj,...,swn},客观权向量为OW={ow1,ow2,...,owj,...,own},则参数的综合权向量为ω={ω1,ω2,...,ωj,...,ωn},其中:
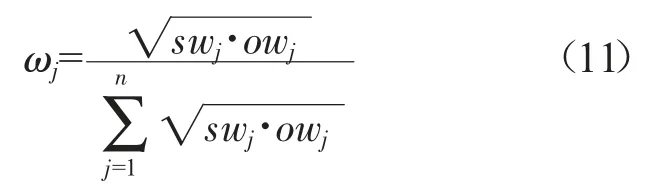
3.2.3 前景理论综合前景值的计算
在具有风险和不确定条件下进行选择时,专家的行为并非完全理性,评价结果与其心理风险感知有关,本文引入前景理论[18]将专家的主观心理偏好纳入弹性供应商选择中。基于前景理论,各弹性供应商的综合前景值Vi由前景决策矩阵中各弹性供应商对于各参数的前景值Vij和参数综合权重ωj共同决定。
3.2.3.1 前景决策矩阵构建
前景决策矩阵构建的核心是计算价值函数v(x-r)和决策权重函数ω(p)。价值函数v(x-r)计算方式如下:
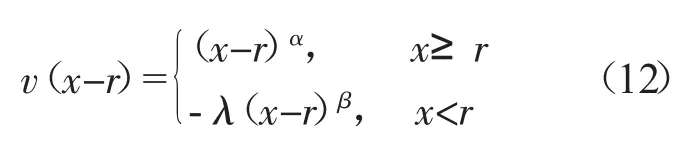
决策权重函数ω(p)计算方法如下:

其中,p 为判断概率,考虑突发事件下弹性供应商问题由专家评价,故将本文计算的专家权重φl视为判断概率p;γ 为风险态度系数,根据Tversky和Kahneman[36]实验验证得参数γ 的最优取值为:γ=0.61。
则前景决策矩阵中各弹性供应商ui相对于各参数ej的前景值为:
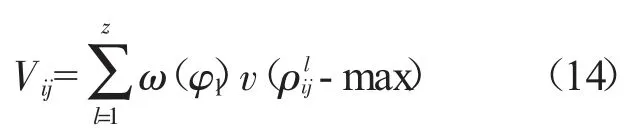
其中,i=1,2,...,m;j=1,2,...,n。
3.2.3.2 综合前景值计算
基于参数综合权重和前景决策矩阵,各供应商ui的综合前景值可通过下式计算:
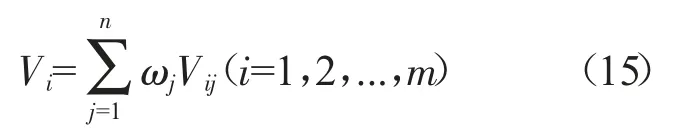
4 实例分析
4.1 实例背景
M公司一家主要设计生产加工高新技术医疗设备和新型精密医疗仪器的公司,并销往全球各地。随着制造全球化和知识经济的发展,为应对市场环境变化,M公司选择自己专注于生产核心部件,而从全球角度配置非核心流程的优质原材料及零部件,降低成本的同时对供应商依赖性增强。然而,M公司的供应链网络数量庞大且跨越全球,国际供应商易受到突发事件的影响,导致供应链中断。近年来频发的突发事件也使得M 公司在选择供应商时更加聚焦于适应不同需求的“弹性”指标,以改善供应链风险管理,有效地预防和应对突发事件造成的中断。M公司对供应商的要求有:能够承受供应链网络的中断,通常有一个现成的或者可以快速实现的替代商;能够对市场变化做出快速反应,通常有一个能快速处理意外或不稳定需求的合作伙伴;只包含少量或不包含浪费,以较少的投入提供高价值的产品;能够灵活地适应外界的干扰而没有较高的成本或较长的交货时间。因此,M公司选择具有稳健性(robust)、敏捷性(agile)、精益性(lean)和柔性(flexible)这四个指标组成“RALF 标准”作为弹性供应商评价指标。M 公司根据要求对候选供应商进行评估,最终有三家供应商可供选择,并邀请三位专家根据“RALF”这四个指标来选择最优供应商。假定U={u1,u2,u3}为三家备选供应商组成的集合,E={e1,e2,e3,e4}为描述供应商弹性的参数集合,其中四个参数分别表示“RALF”四个指标,三位专家集合用R={r1,r2,r3}表示。现在M公司基于三位专家给出的供应商弹性指标的数据对三家供应商进行评价并做出合作决策。其中,专家给出的参数的主观权重向量为sw={0.1,0.5,0.3,0.1}。
4.2 群决策过程
步骤1:构建表示专家对三家供应商弹性评价信息的区间值中智软集合(F1,E),(F2,E)和(F3,E)。


步骤2:本实例参数均为效益型成本,故无需对(Fl,E)(l=1,2,3)进行标准化处理。
步骤3:依据公式(7)计算专家权向量。
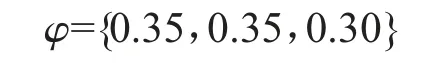
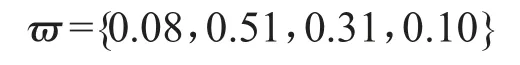
步骤5:依据公式(14)构建前景决策矩阵。

步骤6:依据公式(15)计算各弹性供应商的综合前景值Vi。

步骤7:依据各供应商的综合前景值对其进行排序并做出选择决策。
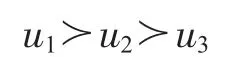
因此,u1为最优弹性供应商,u2次之,u3最劣。
5 研究结论
本文提出方法的优越性和创新性主要表现为以下四点:
1)选择可以充分描述多维不确定和冲突信息的区间值中智软集合作为弹性供应商选择的基本方法,以应对突发事件下的复杂不确定环境。同时,相应地提出了区间中智软集合的确定程度、冲突程度以及邻近度测度概念及方法。
2)考虑到参数重要程度的差异,采用组合赋权方式对参数赋权。具体地,主观权重由专家直接给定,客观权重用熵权法计算得出,进而基于最小信息熵原则将主观和客观权重相结合得到参数综合权重。
3)采用群决策方式对供应商进行评估,以更加全面客观地分析供应商的弹性指标状况,其中专家权重根据区间值中智软集合的邻近度进行测度。
4)充分考虑了突发事件下决策者的非理性因素对供应商弹性评价结果的影响,基于前景理论构建了弹性供应商选择模型。
