基于滑模理论的燃气轮机控制系统容错控制方法研究

2022-05-08刘玉珍

现代工业经济和信息化 2022年3期

刘玉珍

（华北电力大学，北京 102206）

引言

燃气轮机作为旋转叶轮式热力发动机，在现代工业领域是一种十分重要的能量转换和传递装置[1]，在飞机、舰船等航天领域及发电等行业有广泛应用。发电用燃气轮机的控制系统规模大、参数多且结构复杂。燃气轮机正常运行过程时，与发电厂汽轮机相同的是，内部有高温高压的气体；为了与电网频率相匹配，它同时也具有很高的转速；由于其高出力，机械应力及其热应力也很高。以上可以看出，燃气轮机工作环境较恶劣，它还可能会遭受周围环境的污染。在这种情况下，它的主要部件会随着运行时间的增加产生各种各样的性能衰退或损伤，如污垢、泄漏、腐蚀、热畸变和外来物损伤等[2]，并易引发各种严重的故障发生，任何一个局部的故障就可能引起机组的安全性事故甚至导致整个系统的崩溃，造成巨大的经济损失。故我们必须在系统故障时及时进行控制系统的故障诊断与隔离，确保系统具有一定的故障应对能力，从而最大限度保证机组的安全平稳运行。因此，容错控制系统对于将来燃气轮机控制系统的发展具有举足轻重的重要意义[3]。相较于一般控制系统，容错控制系统具有更快地对故障反应速度，也具有更可靠的故障处理能力，进而保障系统在故障下仍能在允许性能范围内运行。

1 燃气轮机控制系统建模

典型的燃气轮机主体主要由五部分组成，即压气机、燃烧室、透平、回热器和转轴，透平即与发电机直接相连的动力涡轮机。燃气轮机发电过程简单来说就是空气经压气机压缩到一定压力后被送入燃烧室，再与燃料混合并在燃烧室中充分燃烧，产生的高温高压的燃气，再进入透平中膨胀完成做功过程，进而完成由热变功的热力循环。做完功的乏气排入回热器，用来预热从压气机进入燃烧室的空气，从而可以降低燃烧过程中所需的燃料量，提高系统燃烧效率。透平中所产生的功一部分是用于驱动压气机，其余部分用来带动负载，即带动与燃气轮机同轴的发电机发电。

参照燃气轮机实际物理过程我们可以得到以下微分方程：

式中：Mm为回热器参与空气与乏气换热的金属质量；cm为回热器金属壁面的比热容；Tm回热器金属壁面的平均温度；Gt为透平的质量流量；cpg为燃气的定压比热；T4为透平排气总温；T22、T44分别为回热器冷端、热端排气温度；Gc为压气机的质量流量；cpa为空气的定压比热；T2为压气机出口总温；p3燃烧室内部压强；Rm燃气平均气体常数，J/kg；cvm为燃烧室内气体平均定容比热容；T3燃烧室内部温度，℃；Qu为燃料低发热量；Kb为燃烧室燃烧效率；Gf燃烧室的质量流量；n 为转子转速；Vcham为燃烧室容积，m3；J是转子的转动惯量，kg·m2；Pt为透平输出功率，kW；Pc为压气机消耗的功率，kW；Pld负载功率，kW。

基于30 kW 微型燃气轮机的工况[4]，并基于以上非线性化模型，我们选取状态变量如下：回热器金属壁面的平均温度，透平入口压强，（两者均为滞止参数），转速n。控制输入变量为燃料质量流量Gf。输出变量y 为转速n，即y=x3=n。

利用下式进行线性化：

我们考虑燃气轮机机组在额定工况下即输出功率为30 kW 工况下的线性化模型，可得P=30 时线性化模型的系统矩阵A，控制矩阵B和输出矩阵C，即

系统的状态空间表达式为：

至此，燃气轮机控制系统的线性化模型建立完成，简单且清晰地表示了燃气轮机各参数之间的关系，便于在此基础上应用现代控制理论进行容错控制的分析。

2 滑模容错方案

滑模控制（Sliding Mode Control，SMC），也叫变结构控制，其本质上是一类特殊的非线性控制，且非线性表现为控制的不连续性。这种控制策略与其他控制的不同之处在于系统的“结构”并不固定，而是可以在动态过程中，根据系统当前的状态（如偏差及其各阶导数等）有目的地不断变化，迫使系统按照预定“滑动模态”的状态轨迹运动。由于滑动模态可以进行设计且与对象参数及扰动无关，这就使得滑模控制具有快速响应、对应参数变化及扰动不灵敏、无需系统在线辨识、物理实现简单等优点。滑模控制首先要构造滑模面。

下述滑模理论与状态反馈相结合的理论过程：

滑模控制首先要构造滑模面，让系统状态按照构造的滑模面来运动。

现构造以下滑模面，以与状态反馈相结合：

令S（k+1）=0，即可构造出滑模面。A，B矩阵分别为离散模型的系统矩阵与控制输入矩阵。

我们定义矩阵G=B+-Y1（In-BB+），可以证明GB=I，将该式代入上面的S（k+1）=0，我们可得到S（k+1）=u（k）-Kx（k）=0，故应有u（k）=Kx（k），因此得出这个表达形式之后要想让系统有较好的相应性能，需要对K即状态反馈增益阵进行极点配置，使得系统故障后仍能有较好的性能指标，结构图见图1。

图1 状态反馈系统结构图

原系统状态空间表达式为

离散化后的模型为

我们考虑系统的恒增益故障，得到故障系统的线性连续定常模型的状态空间表达式，即：

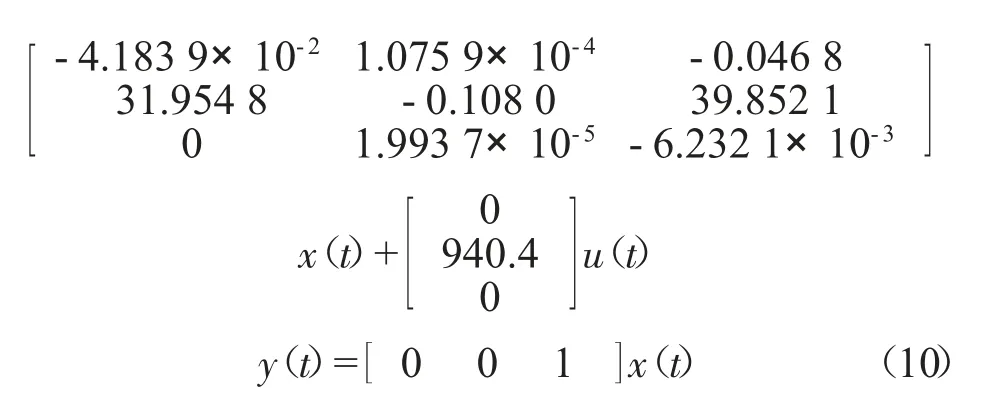
它离散化后的模型为

此时故障模型中我们定义各矩阵分别是G、h和C。

下面我们利用能控判定阵M=[h，Gh，G2h]来对故障后的系统进行能控性判别，通过使用Matlab 中的rank 函数求得M为满秩矩阵，即rank（M）=3。故我们可以得出该系统是完全能控的。所以我们可以利用状态反馈即设计状态反馈来进行任意极点配置。

经过对正常运行和故障时的离散状态空间表达式的特征值的验证，两者的特征值相同，且都在单位圆内，系统仍稳定；进一步对传递函数进行验证，两者的零点不同，故障后的零点在连续模型中数值变小，且传递函数比例增益也变小；在离散模型中其极点变小，增益也变小，故会使得系统响应变慢。因此，我们应通过状态反馈重新配置极点来加快故障后系统的响应，使系统响应加快得到优化。

我们希望通过极点配置令达到故障前或者比故障前更好的输出响应。通过Matlab 仿真我们找到了效果较好的配置极点，即（-0.7，-0.8，-0.9），此时的状态增益矩阵为K=[-1.463 3×109，0.271 9，7.897 8×109]。