生产企业原材料的订购与运输最优方案分析
2022-05-08庞雯文蔡明哲
庞雯文,张 嫚,蔡明哲
(长江师范学院,重庆 408100)
引言
对供应商的供给量及企业订单数据进行标准化处理及正向化处理,并分别建立订货量之和、供货量之和与两者的匹配率等指标构建货物订购评价指标,利用灰色关联分析综合评价模型及Python 软件,对每一个影响因素做出评估,得出最符合的供货商,再建立0-1 线性规划模型,用LINGO 软件对模型进行求解。结果表明,该企业至少选择4 家供货商供应原材料才能满足需求。通过供应商数据,估计出未来24 周各供应商的供应量,并考虑不同材料的不同价格,建立新的0-1 线性规划模型,通过求解,给出了该企业未来24 周每周最经济的原料进购方案。在考虑材料价格的同时考虑运输成本,对上述模型进行修正,制定出损耗最少的转运方案。按要求要使得A 类多、C 类少并且转运商的转运损耗率尽量少,因此,以问题二的0-1 规划模型为基础模型,建立三类材料类型与企业需求相关的0-1 规划模型。通过LINGO 软件对模型进行求解,得到了订购方案和转运方案。
1 问题表述
1.1 问题背景
随着全球经济一体化的发展,生产企业间的竞争也逐渐变得激烈起来,想要在激烈的市场中稳步发展,合理控制成本是关键所在。经过几十年的发展,“运筹学”这一学科体系已经很完善,涉及的数学知识点较多,包括线性规划、整数规划、非线性规划、动态规划、图与网络分析、网络计划技术、排队论、决策分析及对策论等内容[1]。原材料的订购应该从保持企业正常生产、供需平衡、订购种类以及成本价格等方面考虑,选择合适的供应商对企业的生产与收益很重要。企业日常经营管理中时常会面临着如何使得销售成本最低、利润最高,如何规划最高效、最快捷的路线,以及如何实现最高效率的流动资金周转等一系列问题。
1.2 解决问题
为了更好地研究不同情况下的商家采购运输产品的最优解,本文依次提出了以下两个问题:
一是在最符合的供货商中,该企业应至少选择多少家供应商供应原材料才可能满足生产的需求;二是针对此类供应商,制定一个未来24 周中每周最经济的原材料订购方案和损耗最少的转运方案,并在未来24 周每周最经济的方案下,减少转运及仓储的成本,同时希望转运商的转运损耗率尽量少,再次更新订购方案及转运方案。
2 问题分析
企业生产商分析订购货方案的决策研究对生产企业商的成本控制和企业竞争力有着重要影响。如果生产商不能很好地控制原料采购与运输的费用,一定程度上会影响该企业年收入。通过分析供货商的供货数据和转运商的转运数据,从中提炼出有用的变量,并利用这些变量建立灰色关联评价模型和线性规划模型,决策出合适的采购和运输方案[2-3]。
2.1 对问题一的分析
问题一由三个小问题组成。第一个问题要求建立关于供应商和供应数量的0-1 规划模型,以此来研究供应原材料对企业生产的影响。通过问题一的量化分析,挑选出来50 家最重要供应商,计算出满足生产需求的最少供应商,分别将供应A 类,B 类和C 类原材料的供应商计算出即可。在此之前,通过5年间供货商的供货数量预测未来的期望值即供货量,添加不等式作为约束条件,用LINGO 软件求解。第二个问题要求在合理预测的前提下,设置目标函数,并在约束条件下求出各周各供货商的供货量,作为订购方案。第三个问题主要是建立思维模型,要制定损耗量最少的转运计划,就是要解决如何采用合理和相对准确的决策条件,进一步缩小可以选购的转运商[4]。
2.2 对问题二的分析
问题二需要考虑成本、库存和损耗量,要使生产成本和储存成本最低。针对第一个小问题,先从一类产品开始考虑,建立0-1 线性规划模型,在每次模型出现错误后不断改进优化,计入新的产品量,最后得到一个最优策略。针对第二个小问题,如何计算选取供货商得到最经济的订购方案和转运方案。这个过程中需要再次考虑产品是损耗率和成本,得到最优策略[5]。
3 模型的假设
生产商在选择供应商供应产品时不考虑产品的价格问题,不考虑货物损耗问题;供货量可以适当大于订货量,因此可以不用考虑供货量的上限;同一种类企业受相同突发状况因素相同,忽略统一类别企业的内部差异。
4 模型的建立与求解
4.1 问题一的0-1 线性规划模型求解
4.1.1 第一个问题的建模与求解
在第一问的条件下,本部分依据A、B、C 类货物供应商数据建立模型,给出满足生产需求的供应商的最小数量。材料供应商数目庞大,供应种类不单是一种,供应的货物随周数的变化也没有十分明显的规律性。为保证企业能够满足需求的最小值,供应商的个数应当满足0-1 线性规划模型,即对50 家重要的供应商分别从0~50 号进行编号,设为Xi(i=1,2,…,50)。已知企业的产能是28 200 m3/周,需消耗A 原料0.6 m3,消耗B 原料0.66 m3,消耗C 原料0.72 m3,由此可以表示A 原料的产能为m3/周,B 原料的产能为m3/周,C 原料的产能为m3/周。
决策目标:根据以上数据,我们得到生产企业需要支付的供货成本为:
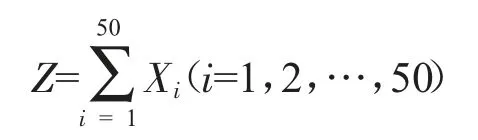
为了经济效益最大化,支付成本必须最小化,因此目标函数为:
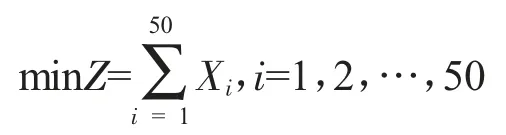
约束条件:
1)要满足企业生产的可能,每周企业生产、B、C的原料之和必须要大于等于企业每周的产能,即:
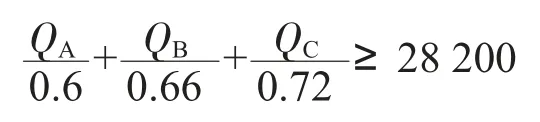
2)Xi代表某企业是否被选择,因此他只有选择和被选择两种情况,即只能有0,1 的结果(0 为未被选择,1 为被选择)。表达式为:
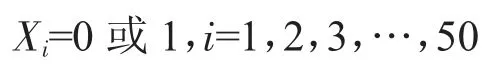
将0-1 整数线性规划模型输入LINGO 求解。可得变量X4、X16、X19、X33=1,即最少选择第140、151、201、348 这4 家供应商,可满足生产需求。4 家供应商的各类指标及数值如表1 所示。
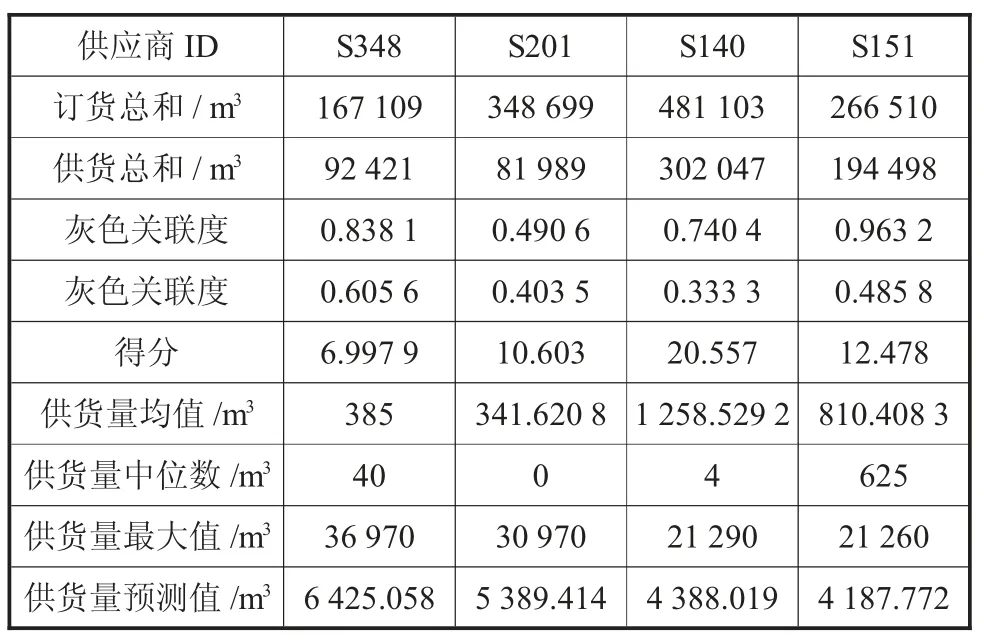
表1 4 家供应商的各类指标及数值
4.1.2 第二个问题的建模与求解
根据402 个供货商240 周的供货量数据表,计算出每一个供货商240 周供货的中位数、最大值、平均值还有方差。根据正态分布相关原理选取正态随机数(注:若取得正态随机数为负值则将其赋值为0),得到未来24 周A、B、C 类每个供应商每周的供货期望值,期望值=,式中:E 为均值,C 为中位数,M 为最大值。402 家供应商的供货量(期望值)通过计算算出。假设A 类产品供应商、B 类产品供应商、C 类产品供应商分别有m1、m2、m3家。设ai(i=1,2,…,15)为50 家供应商中供货A 产品的系数,bj(j=1,2,…,14)为50 家供应商中供货B 产品的系数,ck(k=1,2,…,21)为50 家供应商中供货C产品的系数。再将由正态随机选取得到的未来24 周A 类的供货量设为Pe(e=1,2,…,15),B 类的供货量设为Qf(f=1,2,…,14),C 类的供货量设为Gi(i=1,2,…,15)。已知实际A 类和B 类原材料的采购单价分别比C 类原材料高20%和10%,则可设C 类材料单价为1,A 类材料单价为1.2,B 类材料单价为1.1,假设在一次生产中使用A 类材料为X1、B 类为X2、C类为X3。因此A、B、C 三类产品的供货成本可以表示为1.2X1、1.1X2、X3。
决策目标:根据以上数据,我们可以得到生产企业需要支付的供货成本Z=1.2X1+1.1X2+X3,为了使得经济效益最大化,必须使支付成本最小化,因此目标函数minZ=1.2X1+1.1X2+X3。
约束条件:
1)假设在一次生产中使用A 类材料为X1、B 类为X2、C 类为X3,为了保证正常生产,这一约束条件可表述为:
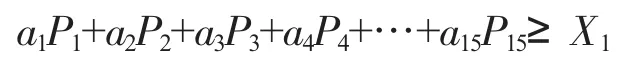
同理可知B、C 需满足:
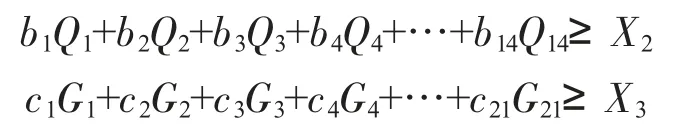
2)考虑到A、B、C 一周共同产能要满足企业一周的正常生产,所以此约束条件可表述为:
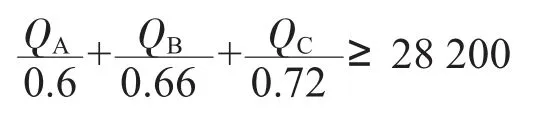
3)分别用ai=1、bj=1、ck=1 表示A、B、C 三类中被选择的供应商,ai=0、bj=0、ck=0 表示未被选择(i=1,2,…,15、j=1,2,…,14、k=1,2,…,21),ai,bj要满足不等式:

将0-1 整数线性规划模型输入LINGO 求解,得到每周最经济的供货方案,对应具体的供货商的供货量和订货ID。
4.1.3 第三个问题的建模与求解
由转运公司的转运耗损率表格可以计算得到各转运公司对应的有效订单次数(α)、非零均值(μ)、非零方差(δ)和中位数(β)等数值。通过240 周的运输时间,要是该运输公司每天都开展运输工作,则其订单满值比应为100%,但实际情况并非全都如此,8家公司中有3 家公司是满订单比值,其余5 家均未达到,(订单损耗量为0 的算作订单次数为0)各自的订单满值比如表2 所示。我们定义非零均值和订单满值比之和为最终评分,根据评分高低我们可以选择出商家所需要的转运商。
由于题目中提到每家转运商的运输能力为每周6 000 m3;且通常情况下,一家供应商每周供应的原材料尽量由一家转运商运输。我们通过A 订购方案看到每周订货量在24 000 m3以下,所以每周至多要4 家转运商转运商品。从表2 的评分中我们可以首先选出评分最高的三家转运商分别为:T1、T5、T7,再从剩余的5 家转运商中选择一家。由于订单次数是体现该转运商工作效率的指标之一,因此同等条件下我们选择订单次数为满数240 次的转运商T2。

表2 所选转运公司指标及指标
综上可知:要使转运商的损耗最少,应当选择T1、T2、T5、T7 四家转运商。
4.2 问题二的0-1 线性规划模型求解
4.2.1 模型Ⅰ
决策目标Ⅰ:转运和存储费用相同,都设为单位1,假设在一次生产中仅使用A 类材料为X1,根据以上数据,我们可以得到生产企业需要支付的供货成本为:Z=1.2X1+2。为了使得经济效益最大化,必须使支付成本最小化,因此目标函数为:min(Z)=1.2X1+2。
约束条件Ⅰ:
1)假设在一次生产中使用A 类材料为X1,为了保证正常生产,这一约束条件可表述为:
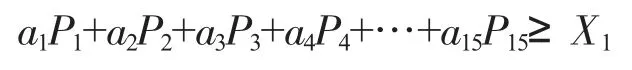
2)考虑到A 一周共同产能要满足企业一周的正常生产,所以此约束条件可表述为:
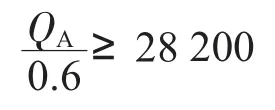
3)分别用a1=1 表示A 被选为供应商,a1=0 表示未被选中,则:
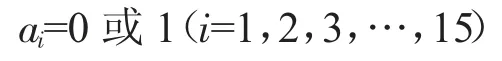
若24 周中每周都有对应解,则24 周同时都选A 即可,若无对应解,则可以选择A、B 两种。
4.2.2 模型Ⅱ
决策目标Ⅱ:转运和存储费用相同,都设为单位1,假设在一次生产中使用A 类材料为X1、B 类为X2,根据以上数据,我们可以得到生产企业需要支付的供货成本为:Z=1.2X1+1.1X2+2。
为了使得经济效益最大化,必须使支付成本最小化,因此目标函数为:minZ=1.2X1+1.1X2+2。
约束条件Ⅱ:
1)假设在一次生产中使用A 类材料为X1、B 类为X2,为了保证正常生产,这一约束条件可表述为:
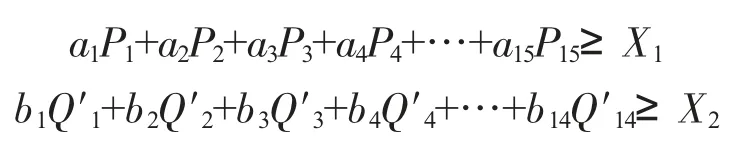
2)考虑到A、B 一周共同产能要满足企业一周的正常生产,所以此约束条件可表述为:
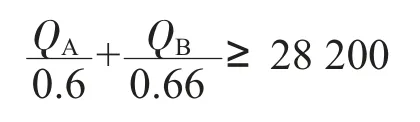
3)分别用a1=1,b1=1 表示A、B 被选为供应商,a1=0、,b1=0 表示未被选中,则:
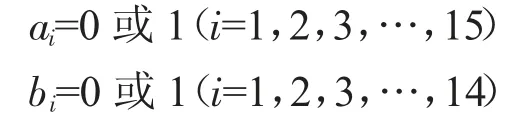
若24 周中每周都有对应解,则24 周同时选A,B 即可,若无对应解,则可以选择C 种。
4.2.3 模型Ⅲ
决策目标Ⅲ:转运和存储费用相同,都设为单位1,假设在一次生产中使用A 类材料为X1、B 类为X2、C 类为X3,根据以上数据,得到生产企业需要支付的供货成本为:Z=1.2X1+1.1X2+X3+2。
为了使得经济效益最大化,必须使支付成本最小化,因此目标函数为:minZ=1.2X1+1.1X2+X3+2。
约束条件Ⅲ:
1)假设在一次生产中使用A 类材料为X1、B 类为X2,为了保证正常生产,这一约束条件可表述为:
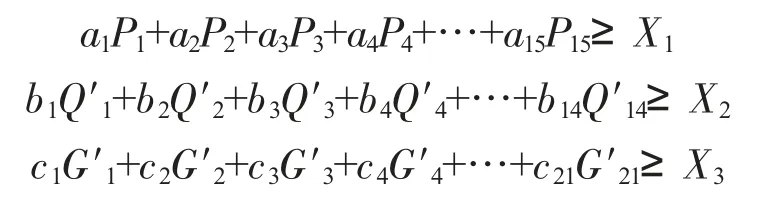
2)考虑到A、B、C 一周共同产能要满足企业一周的正常生产,所以此约束条件可表述为
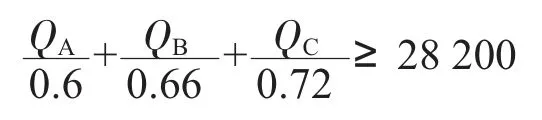
3)分别用a1=1、b1=1、c1=1 表示A、B、C 选为供应商,a1=0、b1=0、c1=0 表示未被选中,则:
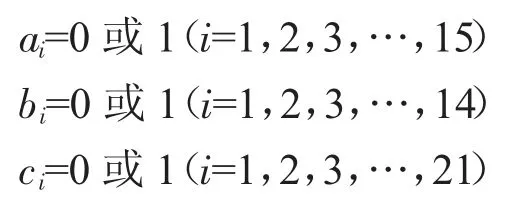
将0-1 整数线性规划模型输入Matlab 软件求解判断这一周是否满足正常生产。若有解存在,则说明这一周A、B、C 类满足正常生产,并根据此模型可一直计算后面的每一周。若没有解存在,则说明A、B、C 类不能满足这周生产,需要改进模型。
5 模型改进
对0-1 线性规划模型进行改进:
1)将仓库至少要有不少于满足两周正常生产需求的原材料库存量也作为约束条件。
2)观察在过去5 年里ABC 类产品给该企业供货的比率是多少,由此得出ABC 类产品在一周的正常生产中各需要多少量,并得到ABC 类分别的供货量区间。
3)通过更精准的方法预测出未来5 年每家供货商的供货量和企业的订货量,这样结合前5 年的数据就得到共10 年数据,通过计算可确定订货量与供货量的差。
6 结语
运筹学与实际生活联系得更加紧密,通过运筹学的思想去解决实际问题,能够更真实、更直观地反映该方案与问题是否切合、是否有效。运筹学配合计算机进行处理实际问题,会使问题更容易解决,提高了企业决策的科学性和可靠性,提高了企业工作的效率,增加了企业的利润。
