基于数字图像连续表示的图像分割方法

娄联堂，汪然然

（中南民族大学 数学与统计学学院，武汉 430074）

近10年来，深度学习被广泛应用于图像分析和图像识别，特别是在图像分割及目标识别方面效果甚至好于传统的图像处理与分析方法，然而，深度学习本质上是一种数据驱动方法，由深度学习获得的结果无法从理论上得到较好的解释，缺少严格的理论支撑.最近，BRONSTEIN M M等人提出了“几何深度学习”的概念，尝试从几何学的角度将机器学习理论统一起来［1-2］.在最简单的情况下，有监督的机器学习本质上是一个函数估计问题，给定训练集某些未知函数的输出，试图从某个假设函数类别中找到一个适合训练的函数φ，使模型可以预测出与测试集的输入对应的输出，机器学习模型可以表示为图1的形式.

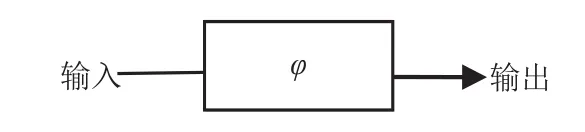
图1 机器学习模型Fig.1 Machine learning model

本文利用数字图像的连续表示［3］方法，研究图像分析和图像识别的深度学习问题，主要探索二维图像分割的通用数学框架.试图找到一个函数φ，使其能够表示基于深度学习的图像分割过程，然后将其应用于复合绝缘子憎水性图像的分割，最后将实验结果与标签进行对比.

1 离散图像及泛函的连续表示问题

深度学习可以看作一个黑箱系统白化的过程（见图1），其中输入可以是一维信号（如语音识别），也可以是二维图像（如图像分割及图像识别），输出可以是特征或识别标签.本文主要研究二维图像的分割或目标识别，现考虑用一个有限矩形区域I×J上的二元连续函数f（x，y）表示输入图像，同样，输出的标签图像可以用I×J上的二元连续函数l（x，y）（深度学习过程中未二值化的标签）来表示，黑箱系统可以用函数空间C（I×J）上的连续泛函φ来表示.给定一组训练样本：

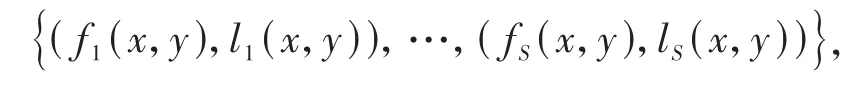
其中S表示训练样本的个数，则对于离散图像的分割任务，训练样本的优化模型可表示为：

其中，w和h分别表示离散图像的宽度和高度.

如果使用均方误差，对于连续的图像，深度学习本质上可以看作求解下面的优化问题：

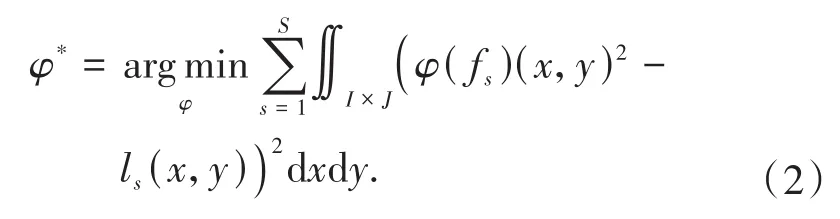
本文研究的是连续泛函φ的表示形式，但若不对连续泛函φ的形式进行限定，（2）式的优化问题一般是很难解决的，同时，要将（2）式应用于二维图像分割或图像识别中，需要解决离散图像的连续表示及连续泛函φ的表示问题.本文主要研究（1）式中泛函φ的连续表示形式.

对于离散图像f（x，y）（1≤x≤w，1≤y≤h），对其四周进行扩展，可令在x=0，x=w+1，y=0，y=h+1时，f（x，y）=0，为方便，扩展后的数字图像仍记为f（x，y）.另外考虑到离散数字图像的带宽有限，并且当m，n较大时，高频分量Fm，n较小，趋近于0，可忽略不计，假设m，n的最大值分别为M，N（1≤M≤w，1≤N≤h），则数字图像f（x，y）可近似表示为：

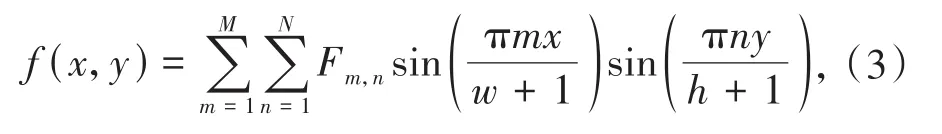
其中：

x和y的取值范围分别为：0≤x≤w+1，0≤y≤h+1，当M和N足够大时，这种数字图像连续表示方式的误差任意小.（3）和（4）式实现了离散图像f（x，y）的连续表示和重建，由（4）式的数字图像f（x，y）计算得到Fm，n后，通过（3）式重建图像，得到数字图像的连续表达式：

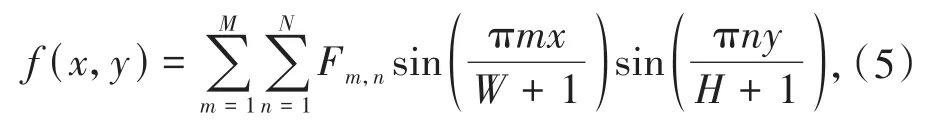
其中（x，y）∈[0，W+1]×[0，H+1]，W，H分别为重建后的图像宽度和高度.

下面考虑（1）式中泛函φ的连续表示问题.由（5）式知，连续图像f（x，y）由它的离散频谱F1，1，…，F1，N，…，FM，N唯一确定，因此泛函φ（f）可以简化为RMN→RMN的一个映射φ（F1，1，…，F1，N，…，FM，N），简记为φ（F），其中F为离散图像的频谱.由（3）和（4）式可知，φ（f）（x，y）可表示为：

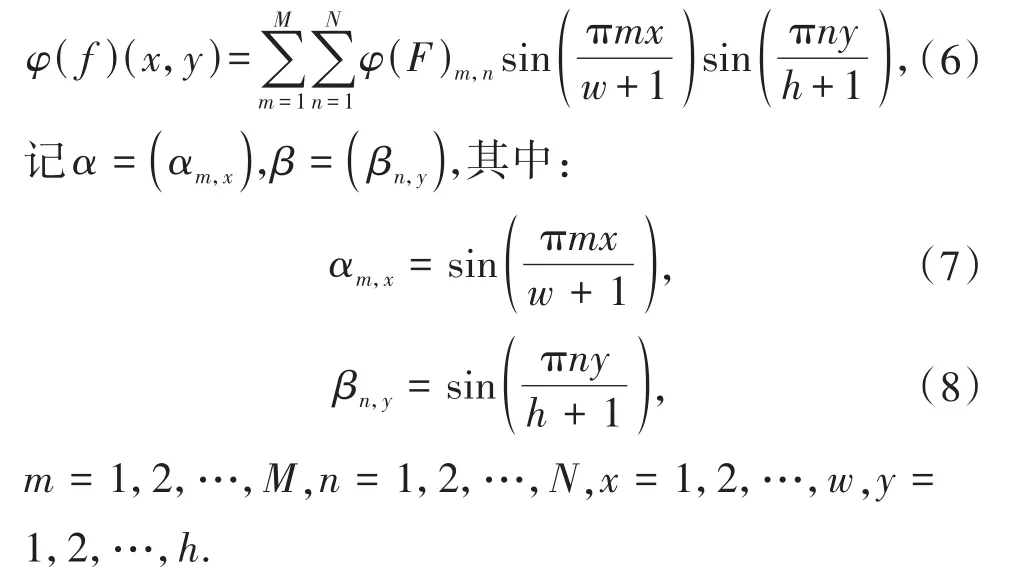
由矩阵乘积的性质可知，公式（6）可表示为如下形式：

则优化模型可表示为：

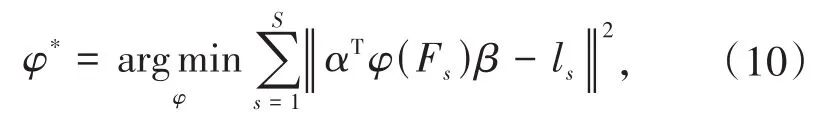
2 优化模型的约束条件及求解

经过以上处理，虽然将空域上的连续优化模型转化为频域上的离散优化模型，连续泛函φ（f）也表示成了函数的形式，但如果不对φ（F）进行一些限制，上面的优化问题仍然无定解.在对φ（F）进行限制前，先取M=N，于是φ（F）是RMM→RMM上的一个映射，为了简化模型的求解，本文对φ（F）增加两个约束条件：

（i）φ（F）是M×M维矩阵空间到M×M维矩阵空间的映射；

（ii）φ（·）是定义在有限区间[0，G]上的满足狄利克雷边界条件的连续函数（G为常数）.

即把φ（F）看作是一个矩阵函数，下面根据矩阵的性质对φ（F）进行简化.由条件（ii）知：

其中：

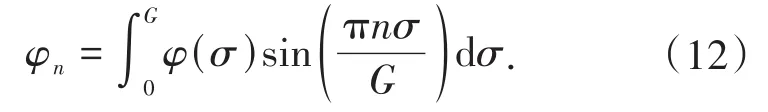
由此φ（F）形式上可以表示为：

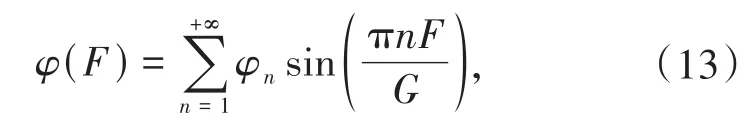
利用正弦级数展开式及方阵F的特征多项式性质，φ（F）可以表示为：

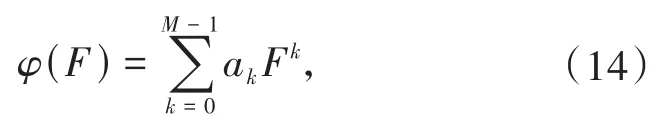
于是在约束条件（i）和（ii）下，优化问题可简化为：

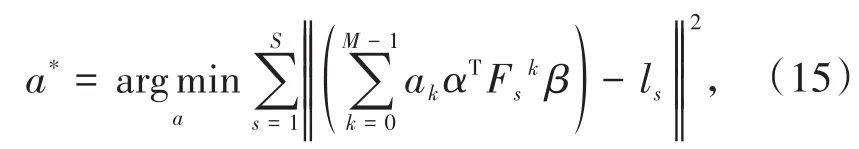
其中aT=（a0，…，aM-1），以上优化问题等价于求解下面的超定线性方程组：

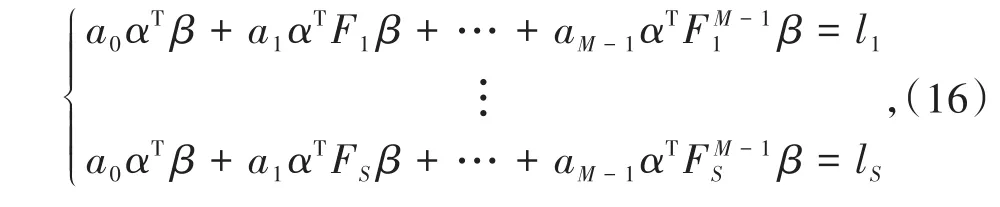
上述方程组简记为：

其中：

考虑到直接法和迭代法均不适用于求解方程个数太多的方程组［4-5］，本文通过构建一个两层BP神经网络模型（见图2），将方程组求解的问题转换成神经网络的参数优化问题［6-7］，即通过误差函数最小化来求解（17）式.

图2 BP神经网络模型Fig.2 BP neural network model

记A=（Ai，j）Swh×M，Ai∈(A1，…，ASwh)∈R1×M，Ai是矩阵A的行向量，bi是（17）式中常数项矩阵b的第i个元素.在（17）式中，{（Ai，bi），i=1，…，Swh}可以看作神经网络的训练样本，训练样本个数为（17）式中方程的个数，相应的网络权值为a=（a0，…，aM-1）T.具体训练步骤如下：

步骤1定义一个损失函数E来监控（17）式的求解过程，本文选用均方误差作为损失函数：

步骤2网络初始化：给变量a赋一个初值，选取学习率α，设定迭代次数；

步骤3将矩阵系数A以及常数项矩阵b分别作为BP神经网络的输入和期望输出；

步骤4计算误差梯度：为使损失函数收敛到0，运用梯度下降［8］的思想，让它沿着负梯度方向下降，对其求导得：

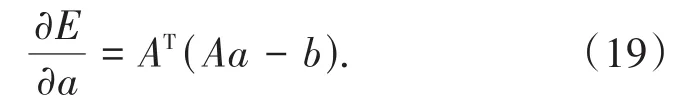
步骤5进行网络权值的更新：

步骤6迭代结束，输出网络权值，即方程组的解.

3 实验

3.1 复合绝缘子憎水性图像分割

为验证本文方法的可行性，将模型用于复合绝缘子憎水性图像分割.本文实验所用图像由某电力公司提供，较为全面准确，等级分为HC1～HC5，图像的大小均为256×256.文中选取的样本总数为135，其中训练样本数为20×5（每个等级取20幅图像），测试样本数为7×5（每个等级取7幅图像）.为避免因光照和水珠的透明性带来的影响，采用直方图均衡化［9］对憎水性图像做增强处理，以突出图像中的水珠（或水迹）区域，然后再将数据输入神经网络.

将数据输入神经网络之前，需要消除训练样本间的数量级差异，以保证结果的可靠性.将（17）式中（k=0，…，M-1，s=1，…，S）的元素归一化到[0，1]区间内，采用的归一化方法为：

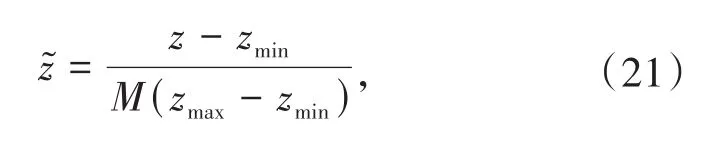
其中，z为归一化前的数值，是归一化后的数值，zmin和zmax分别为矩阵β元素中的最小值和最大值.

此时，求解（17）式可转化为求解方程组（22）：

本文方法选取的学习率为0.1，迭代1×105次，M为50，w和h为256，（5）式中重建后的图像大小为256×256，初始的网络权值是从服从正态分布的数值中选取的随机数.参数设定完成后，利用步骤1～步骤6训练神经网络，得到方程组（22）的解.

3.2 性能评估

为更加客观地评价本文模型分割图像的性能，选用Dice系数［10］评价本文方法.Dice系数是一种集合相似度度量指标，用于计算两个集合间的相似度，取值范围为[0，1].分割效果最佳时取1，效果最差时取0.Dice系数的表达式为：

其中P表示模型的分割结果，R表示模型的真实标签.

3.3 实验结果

训练完成后，得到的模型均方误差如图3所示，实验结果如图4所示.图3给出了损失函数随迭代次数变化的曲线，随着迭代次数的增加，各等级的损失逐渐减少，迭代完成后，各等级的均方误差分别为0.15035、0.15508、0.15572、0.13758、0.02829.图4给出了部分测试样本的实验结果，包含各等级的原始图像、增强处理后的图像、标签图像、本文方法分割结果和Dice系数.

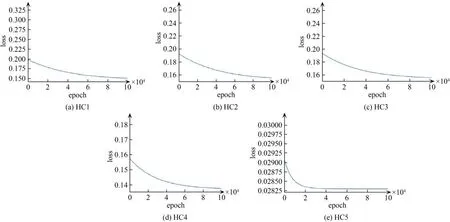
图3 损失随迭代的变化Fig.3 Loss changes with iteration

从图4可以看出，本文方法可以分割出各等级的水珠，其中HC1和HC2的分割效果最好，HC5的分割效果稍差.与标签图像相比，本文方法分割出的水珠要多，特别是水珠形态较好的HC1和HC2这两个等级，水珠形态比较完整，对于形态稍差的HC3和HC4等级，大颗粒水珠的分割效果较好，边界水珠的分割效果较差，观察图像，发现HC3和HC4等级的图像边界部分的水珠小而且密集，这可能会影响模型的性能.

图4 实验结果Fig.4 Experimental results

进一步分析，发现无论是标签图像还是本文方法的结果，HC5图像的大片水珠区域都没能很好地分割出来，这可能是因为在获取数据的过程中，采用了统一的图像增强方法，虽能有效减少水珠的反光和透明性带来的影响，但不能明显突出不同形态的水珠（或水迹）区域；另一方面，在实际的工程应用中，对憎水性图像分割的目的其实就是为了方便研究人员判断憎水性的等级，研究人员主要根据水珠的形态来区分憎水性等级，只要分割出的水珠形态符合要求，就能满足工程应用的需要，从不同等级水珠的差异性来看，本文方法在某种程度上达到了分割目的.

4 结论

通过构造基于数字图像连续表示的图像分割模型，给出了深度学习模型分割图像的相关函数表达式，实现了图像自动分割.此外，分析了复合绝缘子憎水性图像的分割效果，通过实验验证了本文方法与深度学习模型分割图像的相似性.但还存在着函数φ的约束条件不够充分的局限性，通过约束条件（i）和（ii）虽能有效限制φ的表现形式，使其能够成功地拟合基于深度学习的图像分割过程，但函数φ的真正表现形式仍未知，将来还需进一步探索其表示形式.