一种基于因果关系的惯性制导工具误差系数分离方法
2022-05-08魏宗康郭镇净
魏宗康,郭镇净
(北京航天控制仪器研究所,北京 100039)
0 引言
命中精度作为弹道导弹的一项重要战技指标,受到的影响因素很多,比如制导方法误差、制导工具误差、引力异常、再入误差等。其中,惯性制导工具误差约占整个命中精度误差的60%~80%[1]。因此,建立易于分离的、精确的制导工具误差模型并给出高精度参数估计方法,是提高导弹精度的关键[2]。
传统的制导工具误差是基于速度域上的线性回归模型进行估计的,由于环境函数矩阵各列之间的复线性问题,导致利用最小二乘法并不能得到准确的估计。为解决该问题,现有文献提出了两类方法:1)使用Bayes估计,这种方法最大的缺点就是对验前信息依赖性太强,估计结果可能会不准确;2)使用主成分估计、岭估计、偏最小二乘估计等不同的估计方法,这些方法的核心思想是在模型不降阶的前提下估计出系数的近似解,带来的问题就是估计有偏差[1,3-5]。但是,这些方法都没有从根本上解决惯性制导工具误差系数的精确分离问题。
本文针对该问题提出了一种基于因果关系的惯性制导工具误差分离方法,研究内容不再是估计每个系数,而是估计不同相关系数之间组合后的值,采用该方法得到的分离结果更准确。
1 制导工具误差模型及分离难点
制导系统工具误差模型为

式(1)中,Y为遥外测观测输出量,C(t)·X 为Y的主值函数,Y与C(t)·X之差η(t)称为残差。
制导工具误差分离是采用某种手段以便从制导工具误差模型中求解出制导工具误差系数向量的值,最简单直观的手段是基于最小二乘来估计工具误差向量,即
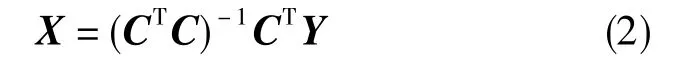
但由于惯性系统误差的环境函数间强线性相关,即结构矩阵C的各列之间存在严重的复共线性,致使信息矩阵Φ=CTC有一些很接近于0的特征值,即Φ=CTC病态,导致用最小二乘估计误差大,分离结果不可信,达不到误差分离的目标。
下面给出实例来具体说明传统方法的不足及本文方法的计算过程和优点。设惯性制导线性系统的归一化系数真值X的各元素为1,由于制导数据量过于庞大,截取其中一小段构成的环境函数结构矩阵C和遥外测观测输出量Y为

可以验证,Φ=CTC的秩为4,Φ为奇异矩阵。此时,采用式(2)将不能解出X的值。
2 基于因果关系相关系数的辨识方法
为了解决环境函数矩阵不为列满秩时的求解问题,提出了主成分估计(Principal Component A-nalysis,PCA)、Bayes估计、岭估计、环境函数矩阵抖动估计、选主元剔次元估计、偏最小二乘估计[1,3,5-7],试图使误差分离结果更准确。
2.1 主成分估计
当C不为列满秩时,则不能用式(2)的最小二乘法求解。所谓主成分估计,就是把信息矩阵Φ=CTC中较小的特征值近似简化为0以改善矩阵病态,然后求解X的过程。
对信息矩阵进行特征值分解,存在正交变换矩阵P= [PAPB],满足

式(3)中,Λ为特征值构成的对角阵,ΛB为Λ中所有非零特征值构成的对角阵,PA为零特征值对应的P中的特征向量,PB为非零特征值对应的P中的特征向量。
误差系数的主成分估计值为

采用上述主成分法对实例求解,非零特征值对应的特征向量及非零特征值矩阵分别为

误差系数的计算值及误差为

可以看出,不能求解出X的真值。
2.2 Bayes估计
Bayes估计(又称为约束主成分估计)的关键是考虑误差系数的验前信息。假设所有误差系数均服从正态分布,验前均值为X0,验前方差矩阵为,则Bayes估计的计算公式[7]为

因此,Bayes估计在理论上存在不足之处,对验前信息依赖性较强,若验前信息不可靠时,估值结果也不可信[5,7]。
2.3 岭估计
岭估计的工作原理是构造新的信息矩阵Φ′,使得其最小特征值距零点远一些,从而改进计算性能。岭估计的计算公式为

岭参数k的大小决定了对条件数改造的程度大小。因此,如何选择合适的k值成为岭估计研究的重心。
对于实例,设k的值由2×10-8逐渐增大到7,信息矩阵Φ′的条件数大幅改善,由2.35×1012减小到6.73×103,如图1所示。

图1 不同k值对应的信息矩阵Φ′的条件数Fig.1 Condition number of information matrix Φ′corresponding to different k

图2 不同k值对应的均方误差值Fig.2 Mean square error corresponding to different k
可以看出,当k的值在10-4~10-2区间内时,均方差相对较小。设k=1×10-3,计算值及估计误差为
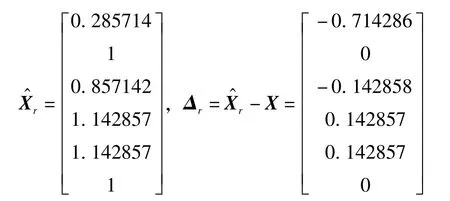
与主成分估计值进行比较,二者近似相等。
但在工程应用中,并不知道真实值X的大小,k的取值具有一定的主观随意性,缺乏理论严谨性。但最根本的问题是,仍然没有克服估计的偏差性。
2.4 环境函数矩阵抖动估计
环境函数矩阵抖动估计的基本思想是对矩阵C做微幅抖动处理

式(7)中,Rd为一个大小与矩阵C相同的随机矩阵, 其每个元素 Rd(i,j)~U(-1,1); (Rd·C)为矩阵Rd与矩阵C的点乘;m为抖动的幅度控制参数。
对变化后的回归模型Y=CdX进行最小二乘估计,结果为

对于实例,设m的值由1×10-7逐渐增大到0.1,信息矩阵Cd的条件数大幅改善,由2.53×1016减小到3.33×104,如图3所示。

图3 不同m值对应的信息矩阵Φ′的条件数Fig.3 Condition number of information matrixΦ′corresponding to different m
由图4可知,当m的值在10-7~10-6区间内时,抖动效果不明显,主要原因是信息矩阵Cd不满秩。当m的值在10-6~10-1区间内时,信息矩阵Cd满秩,当m=1×10-6时,计算值及误差为
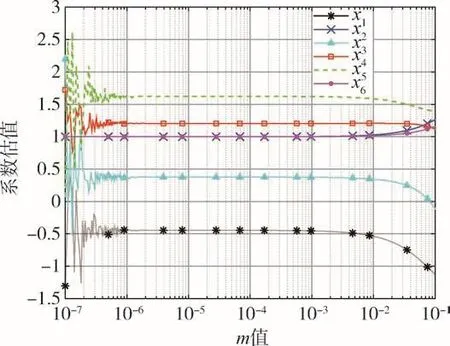
图4 不同m值对应的系数估计值Fig.4 Coefficient estimationcorresponding to different m

但估计效果不理想,均方差接近0.69(大于主成分估计和岭估计的结果)。因此,可以得出结论,采用环境函数矩阵抖动估计计算的值准确性不如主成分估计和岭估计的结果,但三者都不能估计出真值。
2.5 选主元剔次元估计
主成分估计、岭估计、环境函数矩阵抖动估计等方法的一个特点是估计过程没有改变结构矩阵的维数,辨识参数的维数也保持不变,但存在的问题是估计不准确。另外一个思路是改变结构矩阵的维数,对模型进行降维。选主元最小二乘法就是通过剔除接近零的最小特征值对应的环境函数矩阵的列以改进数据处理的效果,即选主元、剔次元。
由于选主元最小二乘法与显著性的思路类似,下面采用该方法对实例进行求解。表示因果关系的方程为

由于信息矩阵CTC为奇异矩阵,对原矩阵依次采用两次环境函数矩阵抖动给出预估值,并进行显著性分析,逐次去掉不显著的系数x5和x4。之所以去掉x5,是因为C5x5对Y的贡献度最小,如图5所示。

图5 输出值及各项系数xi对应的分量CixiFig.5 Output value and component Cixi corresponding to each coefficient xi
第三次估计值时,由于信息矩阵为满秩,不能采用环境函数矩阵抖动法,故直接采用最小二乘法给出各项系数xi的值。为方便起见,设不显著的系数为0,即x4=0、x5=0,求得的系数及误差为
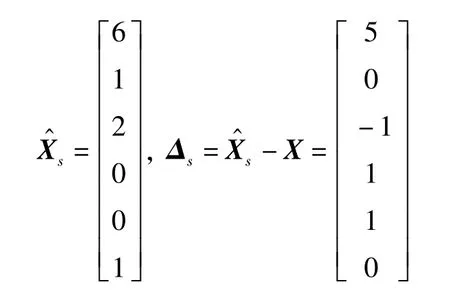
该估计值虽然可以满足Y=CX,但估计的结果与真值差别较大。
2.6 偏最小二乘估计
偏最小二乘回归方法的思路为:
1)设S0=C、Y0=Y,在S0中提取成分t1,令t1=S0·w1。 其中,w1=ST0Y0/‖Y0‖。 实施 S0与Y0在t1上的回归

式(10)中,向量 p1、标量 r1为回归参数,εs与εy为回归残差,有
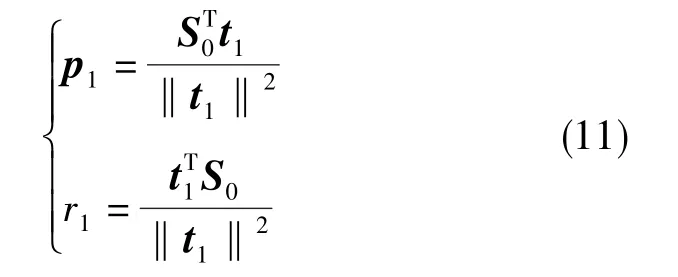
记残差矩阵S1=S0-t1,Y1=Y0-t1r1。如果此时回归方程已经达到满意的结果,则算法停止;否则,令S0=S1,Y0=Y1,对残差矩阵进行新的成分提取与回归。
2)在第h步(h=2,3,…,m),方程满足精度要求,这时得到k个成分t1、t2、…、tk。其中,

可以看出,此处得到的结果与主成分估计、岭估计的结果相同。因此,采用偏最小二乘回归方法仍然没有估计出真值。
综上,这几种方法是目前工具误差系数分离的主要方法,各有特点,然而都无法从根本上避免病态矩阵求逆问题,因而需要为工具误差系数分离寻求新的解决途径。而本文提出的方法通过引入相关系数的概念,将工具误差系数通过因果关系重构成新的误差模型,降低了结构矩阵的维数,并且解决了环境函数矩阵复线性的问题,避免了病态矩阵求逆的过程,可以精确求解出各系数组合值。
3 基于因果关系相关系数的辨识方法
为克服在模型不降阶的前提下对参数有偏估计的不足,本文提出了一种基于因果关系的惯性制导工具误差系数分离方法,其核心思想是在模型中各因子相关的条件下,通过对模型适当降阶以求出各系数组合的精确解[8-10]。
首先,给出相关系数[8]的定义。设一组向量C1、C2、…、Cj线性相关,则存在某些非零标量ri(i=1,2, …,j-1)满足
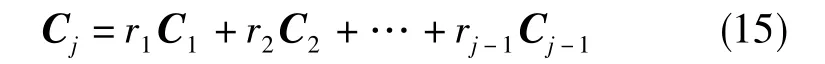
那么,对于向量 Cj与其余向量组 Ci(i=1,2,…,j-1),可以把向量组Ci看做一个n维空间的基,则其相关系数可以写为

其次,将式(15)写成基于相关系数的因果关系表达式
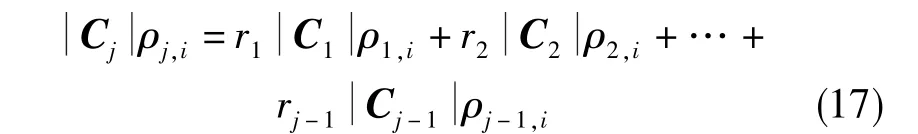
然后根据式(17),将制导系统工具误差模型(式(1))写成相关系数方程组
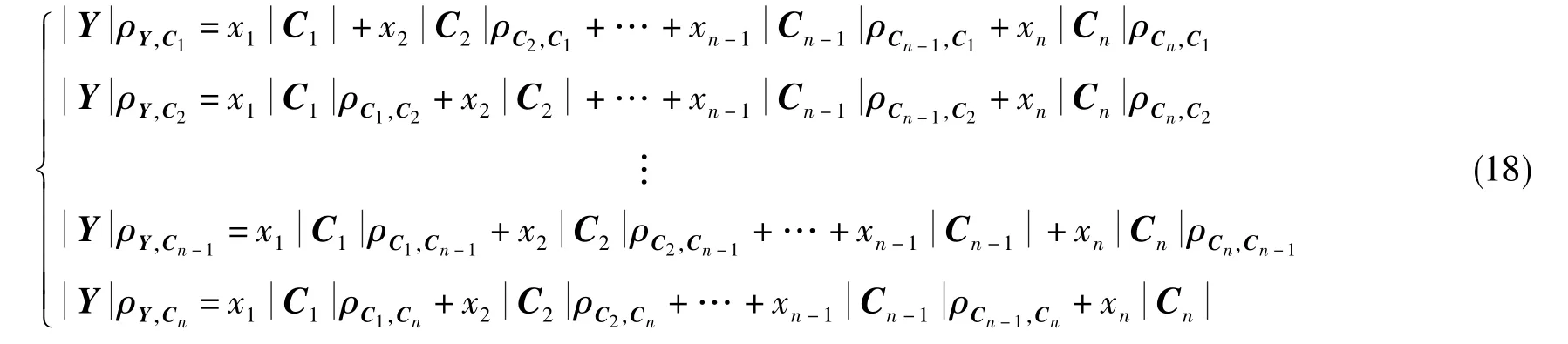
式(18)中,n=1,2,3,…,为参数的维数。
对实例采用式(18)可列写出相关系数方程组,等效为以下矩阵方程

但是,采用传统方法并不能准确求解出6个系数的真值。
因此,采用本文提出的基于因果关系的方法对实例进行求解,求解方法分为试凑法和通用法两种。
3.1 试凑法
由于各系数的组合有多种,所以先通过尝试的方法找到其中一种组合。
经过检验,由C1、C2、C3、C4组成的矩阵为奇异矩阵,令

可列写出相关系数方程组

求解得到的系数为:r4,1=4,r4,2=r4,3=0。由此,有C4=4C1。
经过检验,由C1、C2、C3、C5组成的矩阵为奇异矩阵,令
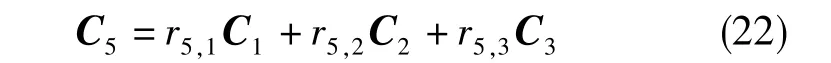
可列写出相关系数方程组
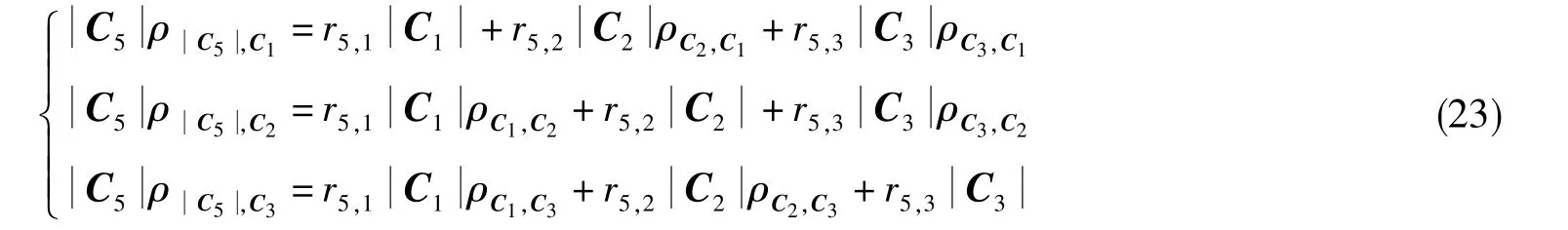
求解得到的系数为:r5,1=r5,3=1,r5,2=0。由此,有C5=C1+C3。
综合以上结果,因果关系可以表示为图6(a)所示。把C4和C5看作中间变量,有

在描述因果关系时,可采用合适的化简方式来去掉中间变量,最后的表达形式如图6(b)所示。
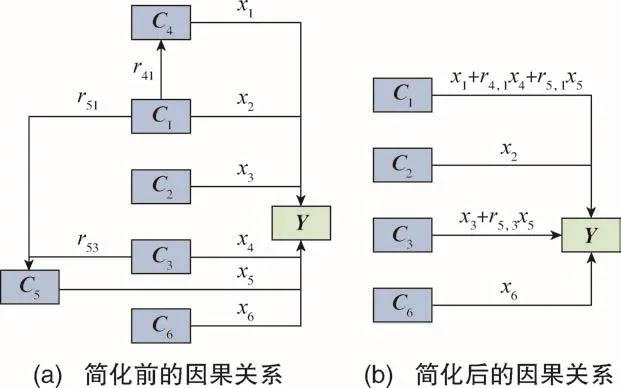
图6 基于因果关系的简化过程Fig.6 Simplification process based on causality
则式(19)可简化为以下因果关系方程组

式(25)可直接求解,有

则误差为

虽然通过以上求解过程最后可以得到各系数组合的精确值,但是过程比较繁琐,不具备普适性和推广性。下面给出一种基于因果关系的通用分析方法。
3.2 通用方法
首先,列出相关系数方程组的结构矩阵

其次,求取结构矩阵的秩

即该结构矩阵不满秩,其基矩阵的维数为4。
然后,通过构造奇异矩阵来寻找基矩阵,若秩数和非零特征值个数相等则找到,否则继续寻找。可以验证,结构矩阵Cρ的第2、第3、第5、第6列可构成基矩阵,即


该方法通过引入相关系数的概念,将工具误差系数通过因果关系重构成新的误差模型,降低了结构矩阵的维数,并且解决了环境函数矩阵复线性的问题,避免了病态矩阵求逆的过程,可以精确求解出误差系数的组合值。
4 结论
传统的制导工具误差分离时,环境函数矩阵各列之间存在复线性问题。为解决该问题,传统方法有:1)基于先验信息的Bayes估计、岭估计,这种方法最大的缺点就是对验前信息依赖性太强,估计结果可能会不准确;2)无需先验信息的主成分估计、偏最小二乘估计等。这些方法的核心思想是在模型不降阶的前提下估计出系数的近似解,带来的问题就是估计有偏差。
本文提出了一种基于因果关系的惯性制导工具误差系数分离方法,通过引入具有因果关系的相关系数,把相互之间有关联的制导工具误差系数进行整合,重构出新的遥外测误差模型。整合后的新系数对应的环境函数矩阵为列满秩,从而精确求解出误差系数的组合值并确保了该值的唯一性,克服了主成分估计、岭估计等传统方法不能精确求解的缺点。把因果关系引入制导工具误差系数分离过程中,克服了结构矩阵维数过多的问题,有利于实时在线计算制导工具误差系数,具有简单快捷、容易实现的优点。
