民用航空惯性基准系统重力补偿方法
2022-05-08王鑫耀李荣冰刘建业
王鑫耀,李荣冰,刘 刚,刘建业
(1.南京航空航天大学导航研究中心,南京 211106;2.航空工业西安飞行自动控制研究所,西安 710065)
0 引言
民用航空在国家发展中具有重要的战略地位,为促进民用航空的发展,国际民航组织(International Civil Aviation Organization,ICAO)提出了所需导航性能(Required Navigation Performance,RNP)的概念。在飞行的各个阶段,RNP运行标准用RNP x表示,x为所需满足的精度性能指标,表示总体系统误差,参考航空无线电技术委员会(Radio Technical Commission for Aeronautics,RTCA)DO-236标准中的精度性能指标分配方法,导航系统的定位精度应优于0.3xnmile。RNP进近(Approach,APCH)是飞行难度最高的阶段,所需精度一般为0.1nmile~0.3nmile。
惯性基准系统在民用航空中是位置、速度、姿态等信息的核心信息源,即使是在卫星失效的情况下,也能在短期内独立完成导航工作并保持可靠的性能[1]。由于民用航空应用的安全关键性,导航系统必须经过严格的测试,以确保其满足RNP各个阶段的指标要求。在导航系统的安全认证过程中,必须妥善处理所有的系统误差,其中的重力模型误差是需要关注的一项,尤其是在纯惯性运行期间。
RTCA制定的全球定位系统/广域增强系统机载设备的最低运行性能标准(DO-229)的附录R(紧组合系统的要求和测试程序)是紧组合系统研制的行业标准。附录R中指出,重力模型误差会导致导航系统误差,特别是在卫星导航失效后的纯惯性工作状态下会产生问题。因此,附录R要求导航系统必须应用某种形式的重力补偿方法,使系统即使在卫星失效的纯惯性工作状态下运行于重力模型误差较大的地区时也能继续约束导航误差。重力补偿能约束由重力模型不准确造成的导航误差,但无法弥补惯导系统本身固有的误差累积。
文献[2]分析了重力误差模型对惯性导航系统精度的影响,文献[3]推导了水平姿态误差与水平重力扰动间的传递函数,但均未对重力扰动进行补偿。文献[4]假设重力扰动符合均匀分布,其重力补偿模型与实际不符。文献[5]使用重力网格数据进行插值补偿,会受到区域限制。文献[6]使用重力梯度仪实时补偿重力扰动,但重力梯度仪的主要用途是在水下,空中的重力梯度变化量不足以支持惯导的补偿。近年来,学者们研究了高阶重力场球谐模型,文献[7]、文献[8]利用EGM2008直接计算重力扰动,但没有涉及地球自转,并未计算真实重力,对重力概念的阐述也不够完整。
EGM2008是美国国家地理空间情报局(National Geospatial-intelligence Agency,NGA)发布的一个地球引力场的球谐模型,由EGM2008所计算得到的在美国和澳大利亚上空的垂线偏差与独立的天体测量值的差异在1.1″~1.3″[9]。基于 EGM2008模型,可以获得高精度的地球引力数据。但由于高阶重力场球谐模型非常复杂,实际应用中存在困难,现有的研究主要集中在重力扰动补偿的仿真验证分析阶段。
针对现有研究中存在的重力补偿模型不准确、重力概念阐述不完整的问题,本文阐述了基于高阶重力场球谐模型EGM2008的完整重力矢量计算方法,分析了惯性基准系统在没有卫星辅助的纯惯性运行期间由重力模型误差引起的定位误差及重力补偿后的改进效果。针对高阶重力场模型在应用场景约束下使用困难的问题,分析了重力模型阶次与性能优化的关系。
1 重力模型误差对惯性基准系统的影响分析
惯性基准系统在导航解算过程中需要载体相对于导航系的运动加速度,而加速度计无法区分运动加速度和重力加速度,加速度计输出的是比力值。由比力提取载体运动加速度的过程称为比力变换,比力方程为

在传统的重力模型下,重力矢量总是垂直于当地水平面,在水平面内没有分量,称之为正常重力矢量[10]。在当地地理坐标系下,正常重力矢量表示为
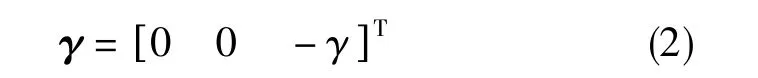
垂直分量γ的大小由Somigliana函数计算得到,其是纬度L的函数

式(3)中,e为椭球偏心率。
由于地球内部质量分布不均匀,真实重力矢量与正常重力矢量间存在重力模型误差,称为重力扰动。重力扰动分为垂线偏斜和重力值异常:垂线偏斜定义为重力矢量与垂直方向的偏差,重力值异常定义为重力矢量大小的幅度误差。重力扰动不是随机误差,而是在局部地区的每次飞行中都会出现的相同的系统误差。
惯性基准系统使用正常重力矢量代替真实重力矢量进行惯导解算时,会因为重力扰动而使运动加速度计算结果存在系统误差并随积分运算影响导航解算结果。速度误差方程为

式(4)中,Φn为姿态误差向量的反对称矩阵,fn和Δn分别为加速度计输出的比力值和零偏在导航系的投影,δg为重力扰动矢量。
相比于重力值异常,垂线偏斜是影响惯性基准系统性能的主要因素,全球垂线偏斜最大在100″数量级,而1″的垂线偏斜相当于5μg的水平重力分量。在惯性器件精度不高的系统中,重力扰动相对于器件误差可以忽略。而随着惯性器件精度的提升,重力扰动与器件误差处在同一数量级甚至高于器件误差,这种情况下的重力扰动不可忽略,有必要采用更高精度的重力模型。重力补偿下的惯性基准系统框图如图1所示。

图1 重力补偿下的惯性基准系统原理图Fig.1 Schematic diagram of inertial reference system under gravity compensation
重力补偿的信息流程为:惯性基准系统向重力场模型提供位置信息,根据位置信息计算真实重力矢量,利用该重力矢量进行比力变换,解算后得到导航信息。需要注意的是,由惯性器件等误差源造成的位置偏差也会引起重力误差,但重力场变化比较缓慢,一般采用网格补偿的形式,所以由位置偏差引起的重力误差相比重力扰动可忽略,本文研究的重力补偿以重力扰动为主。
2 基于EGM2008模型的重力计算方法
地球引力与离心力的合力称为重力,重力矢量可以通过计算重力势能的梯度获得。重力势能由引力势能和离心势能组成

球坐标系下的引力势能可表示为
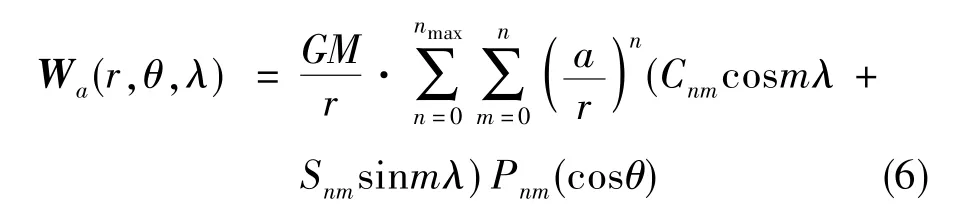
式(6)中,G为万有引力常数,M为地球质量,r为计算点到球心的距离,θ为极距或称为球心余纬度,λ为经度,a为参考椭球长半轴,Cnm和Snm为球谐模型的系数,n为球谐模型的阶,m为球谐模型的次,Pnm(cosθ)为 n阶 m 次 Legendre函数项。
球坐标系下的离心势能可表示为

式(7)中,ω为地球自转角速度。
计算引力势能的梯度
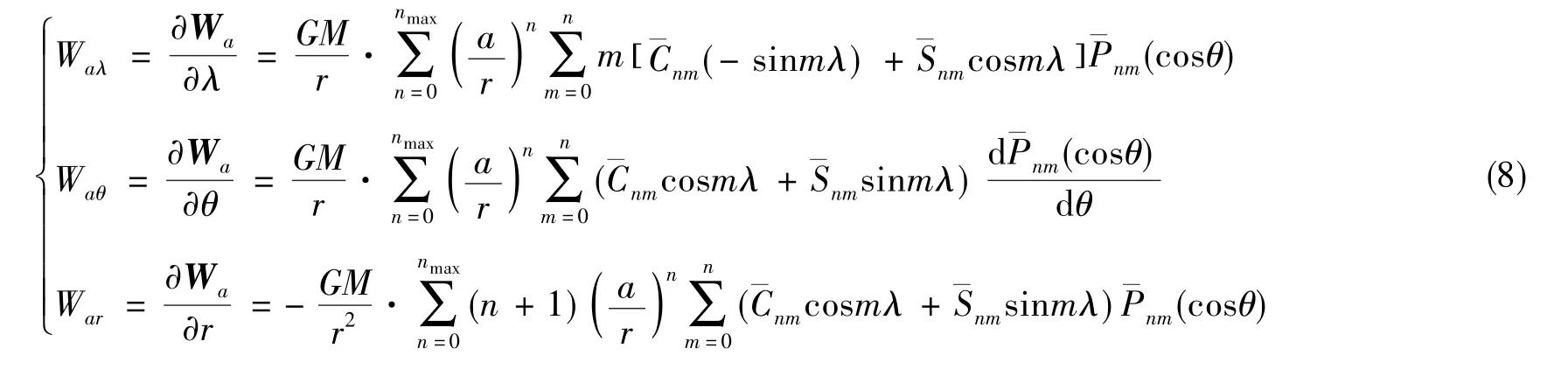
计算离心势能的梯度
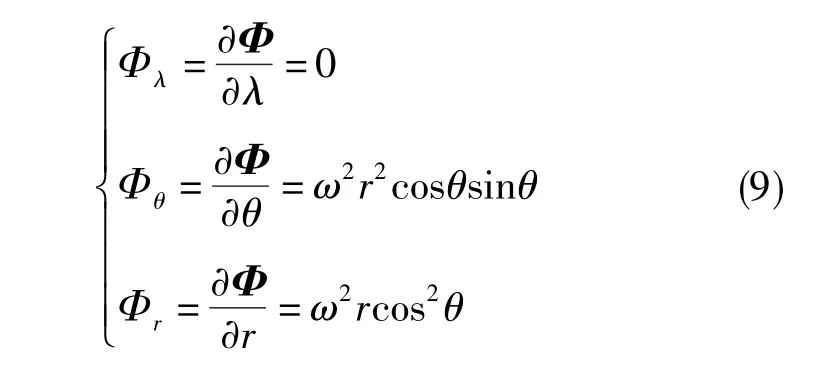
将计算得到的引力势能梯度与离心势能梯度相加得到重力矢量,根据球坐标(λ,θ,r)与球面直角坐标(x,y,z)的转换关系

将重力矢量从球坐标系转换到球面直角坐标系下
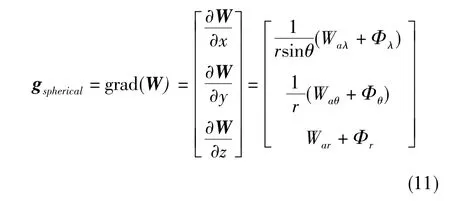
导航解算通常在当地地理坐标系下完成,使用的是大地纬度,而球面直角坐标系使用的是地心余纬度,因此需要将球面直角坐标系下的重力矢量转换到当地地理坐标系下,坐标系的转换关系如图2所示。将球面直角坐标系的y轴反向为y′, (x,y′,z)绕 x(xn)轴转过 - α 角即可转换为当地地理坐标系(xn,yn,zn)。

图2 坐标系转换示意图Fig.2 Schematic diagram of coordinate system conversion
旋转矩阵为


综上,当地地理坐标系下的重力矢量为

式(14)中,R(- β)=diag(1,-1,1)。
需要注意的是,基于球谐模型的重力计算中用到的是完全正常化的缔合Legendre函数,通过递推计算得到。完全正常化的缔合Legendre函数及其导数的递推关系见文献[11]。
为验证本文利用球谐函数计算重力矢量方法的有效性,对全球的真实重力矢量进行了计算,采用WGS-84参考椭球模型,网格分辨率为1°×1°。
计算得到的东向、北向、天向的真实重力矢量分量如图3~图5所示。其中,东向和北向的重力分量较小,采用毫伽(mGal)为单位(1mGal=1×10-5m/s2)。

图3 东向重力分量Fig.3 Diagram of eastward gravity component
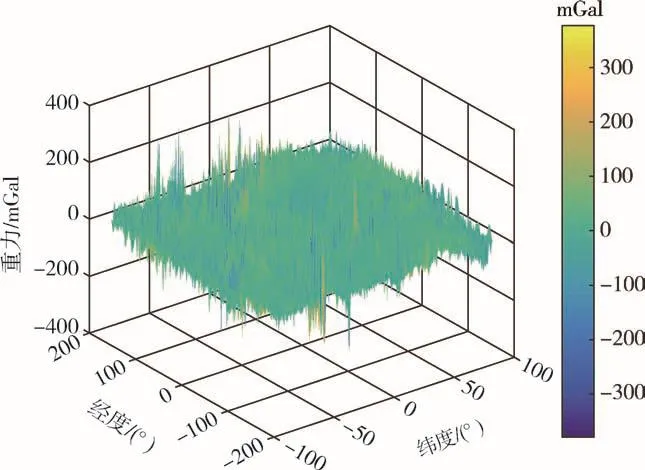
图4 北向重力分量Fig.4 Diagram of northward gravity component
将计算得到的重力矢量大小与国际全球地球模型中心(International Centre for Global Earth Models,ICGEM)提供的重力值进行对比,得到的残差均值为-1.3×10-5mGal,标准差为6.1×10-2mGal,验证了本文重力矢量计算方法的有效性。
本章节完整阐述了基于EGM2008球谐模型的重力矢量计算方法,与文献[7]、文献[8]中的计算方法相比,本文方法补充了对离心加速度和坐标系转换的说明,使重力概念更完整,计算得到的重力矢量可直接用于地理系内的导航解算,不需要再增加额外的计算。
3 纯惯性运行状态重力补偿效果的仿真验证
民用航空对安全性有极高的要求,由于卫星无线电信号容易受到干扰,在卫星信号不可用的情况下,惯性基准系统应当能够独立工作,在短时间内继续保持可靠的性能。在纯惯性运行期间,重力模型的误差不可忽略。
为验证球谐重力模型对纯惯性工作状态下的惯性基准系统补偿的有效性,对某航迹下的导航系统性能进行数值仿真,仿真条件如下:三轴陀螺仪的常值漂移为0.005(°)/h,三轴加速度计的零偏 为 20μg, 航 迹 的 起 点 设 置 为 (30°N,0°E,5000m),飞行器沿30°N纬线以250m/s的速度向东飞行。通常情况下,民用航空要求导航系统有20min的纯惯性运行性能,因此设置仿真时间为20min,飞行距离为162nmile。整个飞行过程中,航向不变无机动,飞机保持平飞,陀螺仪和加速度计的信息由数值解法给出。
根据本文的重力矢量计算方法计算飞行航迹上的重力扰动,重力扰动情况及统计信息如图6和表1所示。
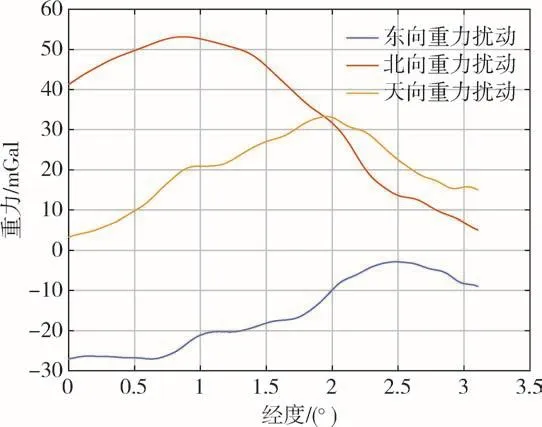
图6 航迹重力扰动情况Fig.6 Diagram of trajectory gravity disturbance

表1 航迹重力扰动数据统计Table 1 Data statistics of trajectory gravity disturbance
在无重力补偿的情况下,设定航迹下的仿真位置误差如图7所示。

图7 无重力补偿的位置误差Fig.7 Position errors with no gravity compensation
相同仿真条件下,采用5′×5′分辨率的重力网格数据对系统进行补偿,每飞过一个网格重新计算一次重力矢量,补偿后的位置误差如图8所示。

图8 5′×5′重力补偿的位置误差Fig.8 Position errors with 5′×5′gravity compensation
从仿真结果可以直观看出,位置误差经过重力补偿后显著减小,导航系统的精度得到有效提高。为进一步分析重力补偿的效果,对仿真结果进行统计,统计结果如表2所示。

表2 重力扰动补偿前后的位置误差Table 2 Position errors before and after gravity disturbance compensation
由表2可知,在民用航空要求的20min纯惯性运行期间,针对特定航线和惯性器件精度水平,重力补偿前的水平位置误差为210.6m,该误差由重力模型误差和器件误差共同引起;重力补偿后的水平位置误差为83.1m,该误差主要由器件误差引起。因此,重力模型误差导致的定位误差为127.5m,占到了水平定位误差的61%,由此可见重力补偿的必要性。
重力模型误差引起的定位误差为确定性误差而非随机误差,该误差在多数航路阶段是微不足道的,但在进近阶段却不能忽略。以RNP0.3的进近为例,分配给导航系统的定位精度应优于0.09nmile(166.7m),该误差占到了导航定位精度要求的76%,因此面对一定的RNP要求,重力模型误差引起的定位误差不可忽略,这限制了惯性基准系统在民用航空中支撑高RNP要求的能力。在采用5′×5′分辨率的重力网格数据补偿后,导航定位精度显著提升,有助于支撑惯性基准系统达到更高的RNP要求。
4 面向应用场景约束的重力模型阶次与性能优化分析
EGM2008模型的阶数为2190,实时的重力计算将对实际应用场景下导航计算机的CPU性能和内存占用带来巨大的挑战。在导航计算机性能不足的情况下,可以牺牲部分重力信息,对模型进行适当裁剪,以达到实时计算的要求。
为验证重力模型裁剪的合理性,采用与本文上一章节相同的航迹,降低重力模型的阶数,分析使用裁剪后重力模型的补偿效果。选择的模型阶数为1600、1000、600、360、180、90、20, 计算航迹上的水平重力扰动,以2190阶的重力扰动为基准,计算降阶后的重力扰动残差,结果如图9所示。

图9 水平重力扰动的残差对比Fig.9 Residuals comparison of horizontal gravity disturbance
由图9可知,360阶以下随着阶数的增加,重力扰动残差有明显收敛的趋势,360阶的残差在5mGal以内,随着阶数继续提高残差收敛的趋势并不明显。
(1)重力场模型阶次与补偿效果关系分析
使用裁剪的重力模型补偿导航系统,忽略了器件误差以避免器件误差的随机性影响效果对比,定位误差的补偿效果如表3所示。
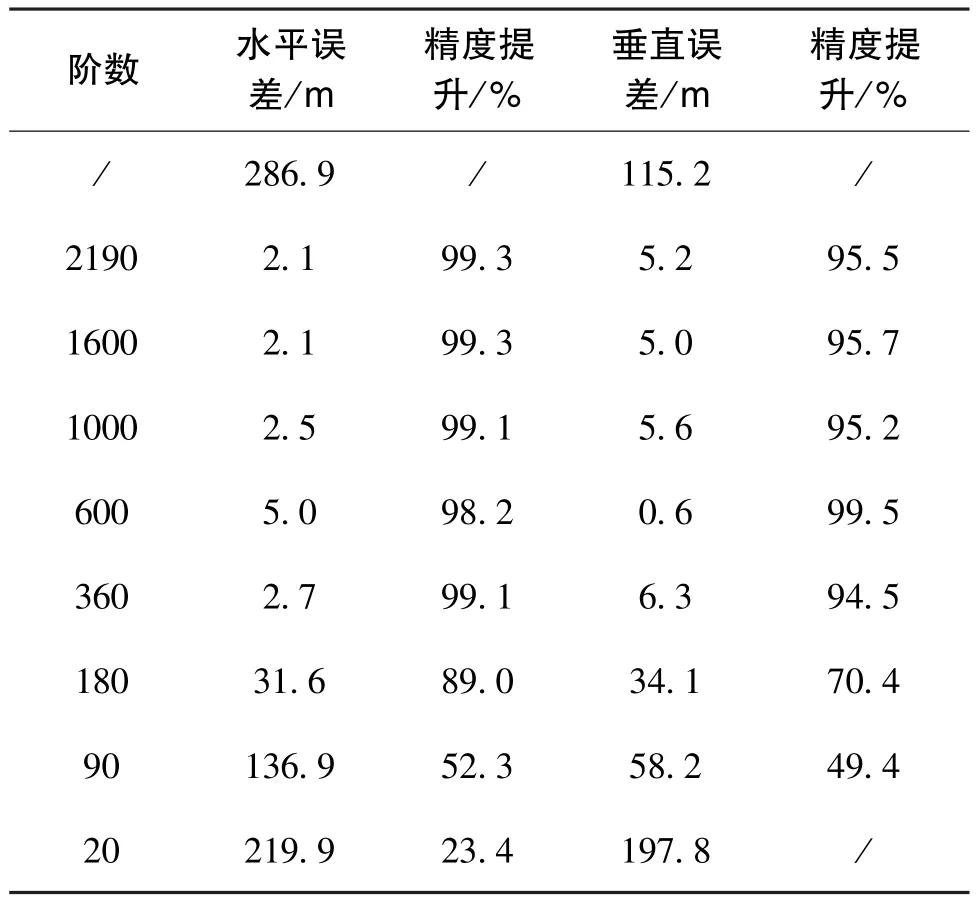
表3 裁剪重力模型的补偿效果对比Table 3 Comparison of compensation effect for cropped gravity model
由表3可知,360阶及以上的重力模型对导航定位误差的补偿效果在90%以上。随着模型阶数的增加,补偿效果并不能获得线性提升,过高的阶数对性能的提升有限,反而增加了导航计算机的负担。
(2)重力场模型阶次与计算机资源占用关系分析
为适应应用场景约束下的导航计算机的性能条件,给实际中的模型选择提供参考,对重力模型的内存占用和计算耗时进行分析,结果如表4所示。模型数据存储在一维数组中,采用双精度浮点数据类型,单次耗时取10次计算耗时的均值。本次计算在PC平台下完成,使用的CPU型号为Intel i5-9300H,由于实际应用场景下的计算性能存在差异,本文计算的耗时仅为相对结果,可为实际应用场景下的重力模型集成提供参考。
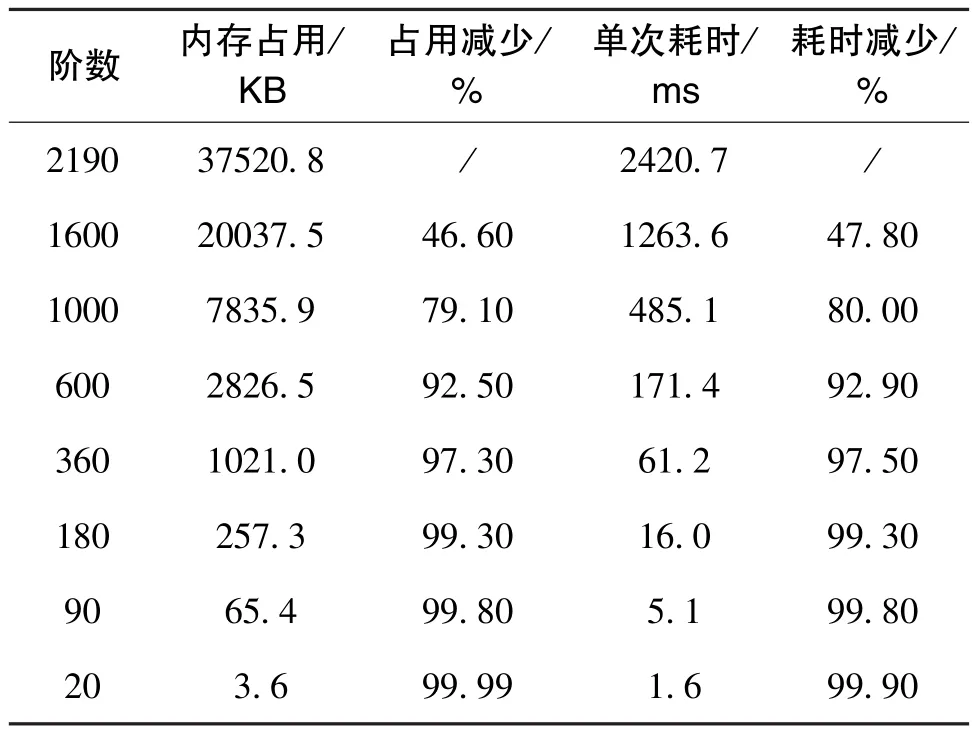
表4 裁剪重力模型的内存占用及耗时对比Table 4 Comparison of memory usage and time consumption for cropped gravity model
重力计算的时间和空间复杂度为O(n2),随着阶数的降低,内存占用和耗时明显减少。实际应用中,应根据导航计算机的内存容量和CPU性能,结合精度要求综合选用模型阶数。
此外,由于重力场变化较为缓慢,采用5′×5′分辨率的重力网格数据足以取得较好的补偿效果,因此不必在惯导解算的每个周期都进行重力矢量的更新,只需在飞行器飞出网格后完成更新即可。对于支持多线程的导航计算机,重力计算可以作为一个单独的线程与惯导解算并发进行,将重力计算的时间分摊到多个惯导解算周期内,从而进一步降低计算机的计算压力。
5 结论
本文研究了惯性基准系统重力补偿技术,阐明了基于EGM2008球谐模型的重力计算方法,并对真实重力矢量进行了计算,验证了计算方法的有效性。通过仿真对EGM2008重力模型应用下的惯性基准系统的性能进行了分析,结果表明:针对特定航线和惯性器件精度水平,在纯惯性运行期间,重力模型误差是一定RNP要求飞行阶段的重要误差源,采用基于EGM2008模型的重力进行惯导解算可使定位误差显著减小,水平定位精度提升达到61%,对满足一定RNP要求的惯性基准系统研制具有支撑作用。最后,面向受约束的实际应用场景,分析了模型阶次与性能优化的关系,仿真表明:在特定航线上使用裁剪模型,在保证精度性能的同时能带来97%的计算效率优化,为实际应用场景下的模型选择提供了参考。
