二维连续型随机变量的条件概率的计算

赵德勤， 宁荣健

(合肥工业大学 数学学院，合肥230601)

1 引 言

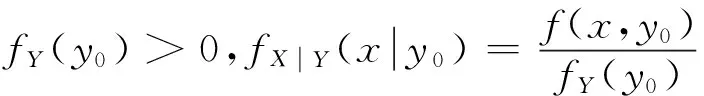
(1)

(2)

将此问题引伸一下.设二维随机变量(X，Y)在区域D内(上)取值，其密度函数为f(x，y)，且当(x，y)∈D时，f(x，y)>0.L为包含在D内的一条光滑曲线，求条件概率

P{a≤X≤b|(X，Y)∈L} 或 P{c≤Y≤d|(X，Y)∈L}.

由于P{(X，Y)∈L}=0，因此不能利用公式

或者

计算.如何计算上述条件概率呢？

为此下面介绍若干种计算方法.

2 主要结论

考虑条件概率P{a≤X≤b|(X，Y)∈L}.

不妨设L的方程为h(x，y)=0，其中h′x(x，y)和h′y(x，y)均连续，且h′y(x，y)≠0.故在变换U=X，V=h(X，Y)下，P{a≤X≤b|(X，Y)∈L}=P{a≤U≤b|V=0}.

定理2设二维随机变量(X，Y)在区域D内(上)取值，其密度函数为f(x，y)，且当(x，y)∈D时，f(x，y)>0.L为D内的一条光滑曲线，其方程为h(x，y)=0，且h′x(x，y)和h′y(x，y)均连续，h′y(x，y)≠0.记u=x，v=h(x，y)，y=H(u，v)，则

(3)

(4)

定理3设二维随机变量(X，Y)在区域D内(上)取值，其密度函数为f(x，y)，且当(x，y)∈D时，f(x，y)>0.L为D内的一条光滑曲线，其方程为h(x，y)=0，且h′x(x，y)和h′y(x，y)均连续，h′y(x，y)≠0.则

(5)

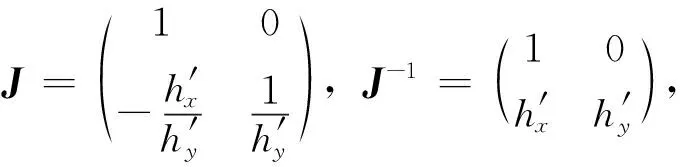
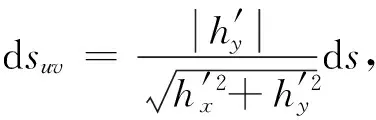
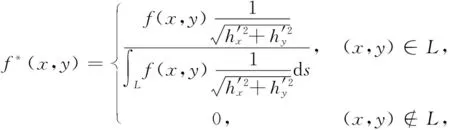
引伸一下，对于曲线型随机变量有下面的定理.

定理4设f*(x，y)为在曲线L上取值的曲线型随机变量(X，Y)的线密度函数，L1⊂L，L2⊂L，且P{(X，Y)∈L1}>0，则

(6)

此外，与条件分布函数的定义相仿，可利用极限求上述条件概率.

(7)

根据具体情况，也可以有

(8)

或

(9)

3 应用举例

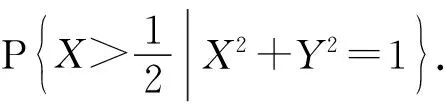
方法1利用等式(3)求条件概率.

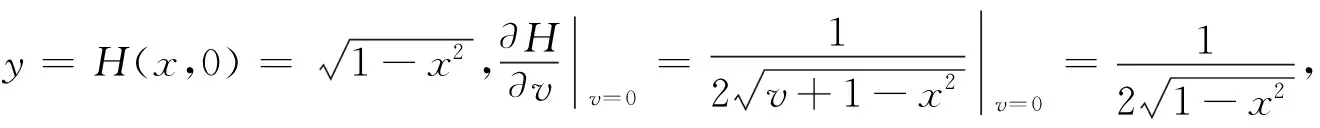
需要指出的是，在方法1中，变换的方式可以是多样的.又解如下.

令X=RcosΘ，Y=RsinΘ，则(R，Θ)的密度函数为

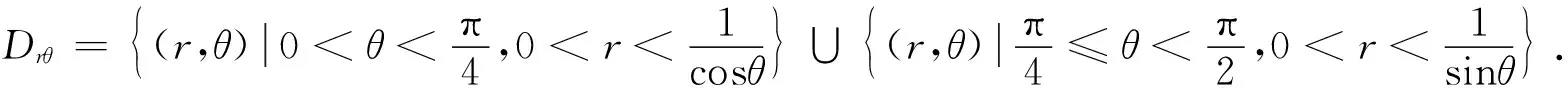
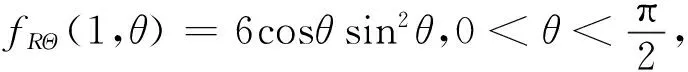
方法2利用等式(5)求条件概率.

方法3利用等式(8)求条件概率.

当ε→0+时，

所以

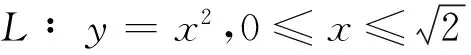
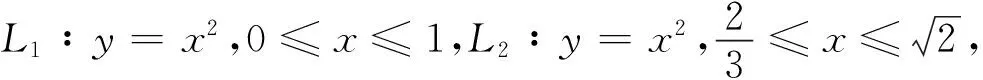
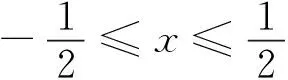
类似这样的问题在工程实际中还有很多，表明该理论具有一定的应用价值.

4 结束语

定理2理论严谨，定理3是定理2的延续.并且通过定理3，在已知二维连续型随机变量(X，Y)落在曲线L上的情形下，由(X，Y)的密度函数f(x，y)得到曲线L上的曲线型随机变量(X，Y)的线密度函数f*(x，y)，丰富了曲线型随机变量的理论.利用极限求上述条件概率的方法思路清晰，但计算量较大，且有一定的难度.

另外，对于条件概率P{c≤Y≤d|(X，Y)∈L}，同样能够得到上述各计算方法.但换一个角度看，当(X，Y)∈L，且h′y(x，y)≠0时，由a≤X≤b可以求出Y的取值范围.例如，在例1中，

如此转化，使得问题变得简单.

问题的拓展：如果二维随机变量(X，Y)既是非离散型，也是非连续型，且在点集D上取值，曲线L⊂D，当P{(X，Y)∈L}=0时，如何计算P{a≤X≤b|(X，Y)∈L}？这个问题还需进一步研究，欢迎感兴趣的同仁共同探讨.

致谢感谢审稿人给出的宝贵意见，感谢唐烁老师对论文的整体结构等诸多方面的指导.