方向导数的计算公式的注记

梁亚娜， 傅守忠， 王世芳

(肇庆学院 数学与统计学院，广东 肇庆526061)

1 引 言

导数的意义是函数关于自变量的变化率.多元函数在某一点沿着一个给定方向的方向导数，实际上就是函数在这个方向上的一种变化率.数学分析和高等数学教材中[1-3]，都是利用多元函数的全微分和方向导数的定义，证明方向导数的计算公式.学生对全微分和高阶无穷小没理解透的时候，很难理解这个证明.

通过坐标平移和坐标旋转变换，将方向导数的计算转化为偏导数的计算，再利用复合函数的求导法则，证明了方向导数的计算公式.这个证明方法的优点是几何上比较直观，但其缺点是不易推广到4元及4元以上函数，因为3维以上的空间无法用几何表示.本文用Schmidt正交化[4]替代坐标旋转，就便于向高维进行推广.

2 预备知识

定义[1，5]设二元函数z=f(x，y)在点P0(x0，y0)的某邻域U(P0)⊂2有定义，l为平面中以点P0为起始点的射线，P(x，y)为l上且含于U(P0)内的任一点，以ρ表示P与P0两点间的距离.若极限

对于三元函数f(x，y，z)，它在空间中一点P0(x0，y0，z0)沿方向l的方向导数，类似可定义为

其中P(x，y，z)为l上的任一点，ρ表示P与P0两点间的距离.

注 显然，函数f(x，y，z)在一点沿x轴正向的方向导数，是函数在该点关于自变量x的“右”偏导数；沿x轴负向的方向导数，是函数在该点关于自变量x的“左”偏导数的相反数.特别当函数在该点的偏导数存在时，沿x轴正向和负向的方向导数，分别是函数在该点关于自变量x的偏导数及其相反数.将x换成y或z，结论也成立.对任意n(n≥2)元函数结论类似.

引理1[1，6]若m元函数f(u1，u2，…，um)在点(u1，u2，…，um)可微，n元函数uk=gk(x1，x2，…，xn)(k=1，2，…，m)都在点(x1，x2，…，xn)具有xi(i=1，2，…，n)的偏导数，则复合函数

f(g1(x1，x2，…，xn)，g2(x1，x2，…，xn)，…，gm(x1，x2，…，xn))

关于自变量xi偏导数都存在，且

该引理是一般多元复合函数的求导公式.

3 方向导数计算公式的新证明

引理2(i)若二元函数f(x，y)在点P0(x0，y0)沿给定方向l的方向导数fl(x0，y0)存在.令

u=x-x0，v=y-y0

是坐标平移变换，则复合函数g(u，v)=f(u+x0，v+y0)在原点沿l的方向导数gl(0，0)也存在，且gl(0，0)=fl(x0，y0).

(ii)对三元函数f(x，y，z)也有类似结论，即对函数g(u，v，w)=f(u+x0，v+y0，w+z0)，有gl(0，0，0)=fl(x0，y0，z0).

证根据方向导数的定义，结论显然.

针对引理2中的函数，由复合函数求导公式易得

引理3(i)当f(x，y)在点P0(x0，y0)的偏导数存在时，g(u，v)在(0，0)点的偏导数也存在，且gu(0，0)=fx(x0，y0)，gv(0，0)=fy(x0，y0).

(ii)若三元函数f(x，y，z)在点P0(x0，y0，z0)的偏导数存在，则对应的函数g(u，v，w)在(0，0，0)点的偏导数也存在，且

gu(0，0，0)=fx(x0，y0，z0)，gv(0，0，0)=fy(x0，y0，z0)，gw(0，0，0)=fz(x0，y0，z0).

定理(i)若二元函数f(x，y)在点(x0，y0)可微，则函数在该点沿任一方向l的方向导数都存在，且

fl(x0，y0)=fx(x0，y0)cosα+fy(x0，y0)cosβ，

其中cosα和cosβ是方向l的方向余弦，即e0=(cosα，cosβ)是方向l同向的单位向量.

(ii)若三元函数f(x，y，z)在点(x0，y0，z0)可微，则函数在该点沿任一方向l的方向导数都存在，且

fl(x0，y0，z0)=fx(x0，y0，z0)cosα+fy(x0，y0，z0)cosβ+fz(x0，y0，z0)cosγ，

其中cosα，cosβ，cosγ是方向l的方向余弦，即e0=(cosα，cosβ，cosγ)是方向l同向的单位向量.

证只证明结论(ii)，结论(i)的证明方法与结论(ii)的类似，或可作为结论(ii)的特殊情况.

根据引理2和引理3，仅需证明在坐标原点的方向导数的计算公式即可，即不妨设(x0，y0，z0)就是(0，0，0).

若l平行于某一坐标轴，由第二节的注可知，结论成立.

若l不平行于任一坐标轴，即α，β，γ∈(0，π)，此时sinα，sinβ，sinγ都是正数，且

cos2α+cos2β+cos2γ=1.

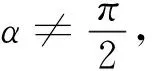
r1=e0=(cosα，cosβ，cosγ)；

(a2，a2)=cos2βcos2α+sin4β+cos2βcos2γ=cos2β(cos2α+cos2γ)+sin4β

=cos2βsin2β+sin4β=sin2β，

=(0，0，1)-cosγ(cosα，cosβ，cosγ)+cotβcosγ(-cotβcosα，sinβ，-cotβcosγ)

=(-cosαcosγ(1+cot2β)，0，1-cos2γ-cot2βcos2γ)

因此

注意到{e1，e2，e3}和{r1，r2，r3}都是3的标准正交基，故其过渡矩阵为正交矩阵，因而

将向量组{r1，r2，r3}构成的坐标系的坐标轴分别记为u，v，w，则空间中任一点(x，y，z)在新坐标系下的坐标(u，v，w)满足

即

令

g(u，v，w)=f(φ(u，v，w)，ψ(u，v，w)，ζ(u，v，w))，

根据已知条件函数f(x，y，z)在点(x0，y0，z0)可微和复合函数求导法

fl(0，0，0)=gu(0，0，0)=fx(0，0，0)φu(0，0，0)+fy(0，0，0)ψu(0，0，0)+fz(0，0，0)ζu(0，0，0)

=fx(0，0，0)cosα+fy(0，0，0)cosβ+fz(0，0，0)cosγ.

得证.

4 结 论

当所给方向与某坐标轴正向一致，且函数在某点关于该自变量的偏导数存在时，方向导数就是函数在该点对该自变量的偏导数.本文利用向量组的Schmidt正交化方法，对所给方向的向量和除某一坐标轴外的其它坐标轴上的单位向量进行正交化，形成一个新的直角坐标系，所求方向导数在此坐标系下正好是对某新变量的偏导数.利用新旧坐标间的线性变换公式和多元复合函数的求导法则，即可得到方向导数的计算公式.该方法对二元和三元函数有比较直观的几何意义.由于Schmidt正交化方法适用于任意有限维的空间，所以理论上推导n(n≥2)元函数方向导数的计算公式都是可行的.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.