含粗骨料超高性能混凝土单轴受压疲劳性能

2022-05-07李力剑徐礼华黄宇雷徐凡丁

建筑材料学报 2022年4期

李力剑，徐礼华，池寅，黄宇雷，徐凡丁

（武汉大学土木建筑工程学院，湖北武汉 430072）

超高性能混凝土（UHPC）作为一种可持续、高性能混凝土材料，具有强度高、耐久性好等优良特性，自问世20余年以来一直为国内外土木工程界所瞩目.迄今，UHPC可分为活性粉末混凝土（RPC）和含粗骨料超高性能混凝土（UHPC（CA））两类.RPC对原材料要求严格，制备工艺复杂，生产成本高，其推广应用受到一定限制.而UHPC（CA）因其原料易取、制备简单、成本较低等优势而更具竞争力，工程应用前景更加广阔.

UHPC结构在长期服役过程中，除了需要在静力荷载作用以及高应力状态下工作之外，还需要抵抗频繁的循环动荷载.这种具有周期性循环特性的疲劳荷载会引起UHPC内部应力场不断变化及重分布，推动内部初始微裂纹的不断萌生和发展，进而引起UHPC力学性能的渐进性劣化，最终导致材料及结构在低于容许应力之下发生疲劳破坏.因此，弄清UHPC在疲劳荷载下的力学行为，对UHPC构件或结构的设计计算至关重要.

UHPC现有研究主要以静力性能为主［1-4］，而对其疲劳性能研究尚属起步阶段.余自若等［5］研究了RPC受压疲劳性能，发现RPC具有优于普通混凝土的抗疲劳开裂能力.在此基础上，方志等［6］研究了钢纤维掺量对RPC受压疲劳性能的影响，发现RPC疲劳寿命和疲劳强度随着钢纤维掺量的增大而提高.现有研究并未考虑粗骨料的掺入对UHPC单轴受压疲劳性能的影响.研究表明［7］，钢纤维以粗骨料为中心环绕分布，粗骨料的掺入会对钢纤维分布产生不利影响.同时，粗骨料的掺入也会引入更多薄弱的界面过渡区，影响材料微结构组成，进而影响材料整体性能.因此，有关RPC疲劳性能的研究成果不能完全适用于UHPC（CA）.本文通过单轴受压疲劳试验，研究UHPC（CA）的单轴受压疲劳性能，探讨其疲劳破坏形态、疲劳变形、疲劳寿命及疲劳强度，建立UHPC（CA）的存活率-应力水平-疲劳寿命（p-S-N）方程，为UHPC（CA）的抗疲劳设计和工程应用提供参考.

1 试验概况

1.1 原材料及配合比

基于课题组前期研究成果［2-3］，UHPC（CA）配合比见表1（其中mW/mB为水胶比1）本文涉及的水胶比、减水率等除特别说明外均为质量比或质量分数.，φsf为钢纤维体积分数）.主要原材料为：P·O 52.5普通硅酸盐水泥（28 d抗压强度58.3 MPa）、矿渣粉（活性指数105%）、硅粉（活性指数130%）、0.212～0.425 mm精制石英砂、粒径5～10 mm玄武岩碎石、聚羧酸系高效减水剂（减水率大于35%）和镀铜光面平直钢纤维（长度12 mm，长径比60，抗拉强度2 750 MPa）.

表1 UHPC（CA）配合比Table1 Mix proportion of UHPC（CA）

1.2 试件设计及制作

为研究UHPC（CA）的高周和低周疲劳特性，本文试验以应力水平S作为主要影响因素，设置0.9、0.8、0.7、0.6、0.5共5个应力水平，每个应力水平包含5个平行试件.选用尺寸为100 mm×100 mm×300 mm的棱柱体试件进行静载和疲劳试验.另外浇筑3个边长为100 mm的立方体试件，用于测试UHPC（CA）的立方体抗压强度.

UHPC（CA）试件的浇筑过程见图1.脱模后，进行48h蒸汽养护，待自然冷却后，移入标准养护室养护至28 d.

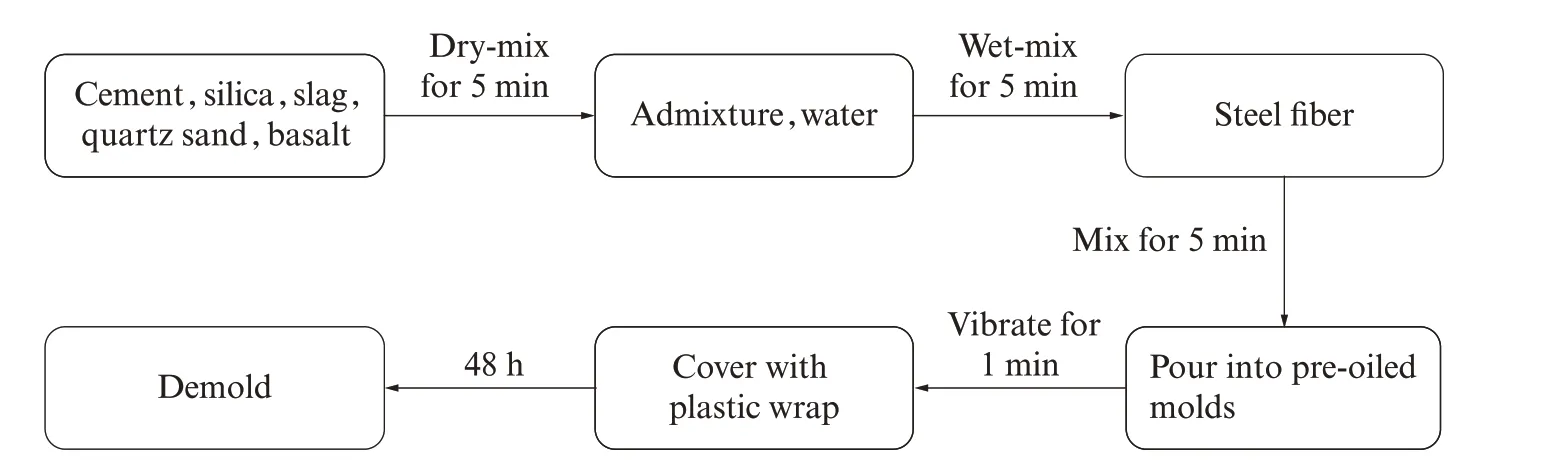
图1 试件浇筑全过程Fig.1 Whole process of specimen fabrication

1.3 加载方案

单轴受压静载及疲劳试验均在MTS 2 500 k N电液伺服四立柱动态加载系统上进行.静载试验采用位移控制，加载速率为0.002 mm/s；疲劳试验采用荷载控制，采用正弦波加载，加载频率固定为5 Hz，最小荷载为Pmin，最大荷载为Pmax，且Pmin=0.1Pmax，疲劳试验加载制度见图2.试验过程中，利用MTS数据采集系统和Flex TestTM60伺服控制器进行数据采集，包括荷载值、位移值和循环次数等.

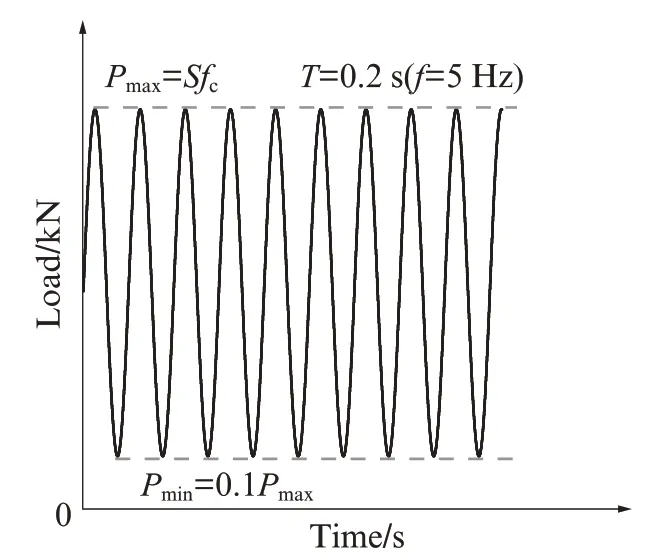
图2 疲劳试验加载制度Fig.2 Loading system of fatigue test

根据GB/T 31387—2015《活性粉末混凝土》，以1.2 MPa/s的加载速率进行立方体抗压强度试验，得到UHPC（CA）立方体试件28 d抗压强度平均值fcu=135.4 MPa；利用位移控制加载，得到UHPC（CA）棱柱体试件抗压强度平均值fc=118.8 MPa.

2 试验结果及分析

2.1 疲劳破坏形态

各应力水平下UHPC（CA）试件的疲劳破坏形态见图3.由图3可见，试件在疲劳破坏时完整性较好，这是由于钢纤维的掺入显著提高了UHPC基体的阻裂能力和变形能力.已有文献表明［5-6］，掺入钢纤维的RPC疲劳破坏形态为单一主裂缝的剪切破坏，UHPC（CA）则呈现1条或2条主裂缝的剪切破坏形态.这是由于粗骨料的掺入引入了粗骨料-UHPC基体界面过渡区这一力学性能的薄弱环节［7］.在疲劳荷载持续作用下，UHPC（CA）内部会有更多微裂纹的萌生和发展，使得试件中微裂纹的分布更加复杂.在宏观响应上，表现为主裂缝分布的多样性.

图3 各应力水平下UHPC（CA）试件的疲劳破坏形态Fig.3 Fatigue failure patterns of UHPC（CA）specimens under different stress levels

UHPC（CA）试件的典型疲劳破坏断面见图4.由图4可见，疲劳破坏断面具有明显的滑移痕迹，断面上可以观察到大量的钢纤维.钢纤维的掺入使UHPC基体裂纹扩展得到了有效延滞，使试件破坏时裂而不散，呈现出延性破坏特征.疲劳破坏断面有2个典型区域：浅灰色的疲劳区和深灰色的裂纹扩展区.粗骨料的掺入，使得UHPC（CA）基体内钢纤维的分布不如RPC均匀.因此，可以明显观察到，疲劳区钢纤维分布较为稀疏.在疲劳荷载作用下，该区域最先开裂后持续受力摩擦，有明显的反复摩擦痕迹，通过扫描电镜（SEM）也可以观察到这一现象.相反，裂纹扩展区钢纤维较多，是基体内部力学性能较好的区域.在试件将要发生疲劳破坏时，裂纹才逐渐由疲劳区发展到裂纹扩展区.因此，与疲劳区不同，裂纹扩展区表面粗糙不平整，没有摩擦痕迹，与静载试验中试件的典型破坏断面相似.

图4 UHPC（CA）试件的典型疲劳破坏断面Fig.4 Typical fatigue failure surface of UHPC（CA）specimen

2.2 疲劳变形

2.2.1 应力-应变曲线

图5为单调和疲劳荷载作用下UHPC（CA）试件的应力-应变曲线，其中疲劳应力-应变曲线剔除了最后一个循环.由图5可知，随着循环次数的增加，UHPC（CA）的疲劳应力-应变曲线不断向变形增大的方向发展.与此同时，越接近疲劳破坏极限状态，曲线斜率越小，这反映了应变增长速率的增大和疲劳模量的衰减.现有研究表明［8-9］，纤维混凝土（FRC）的单调应力-应变曲线可作为其疲劳应力-应变曲线的包络线.由图5可见，该规律并不完全适用于UHPC（CA）.在高应力水平（S≥0.8）下，仍可通过静载变形来预估UHPC（CA）的疲劳破坏变形；而在低应力水平（S＜0.8）下，通过静载变形预估的疲劳破坏变形比实际变形大.

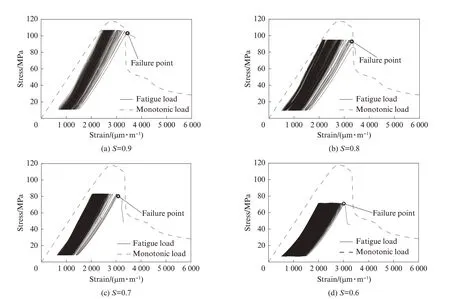
图5 单调和疲劳荷载作用下UHPC（CA）试件应力-应变曲线Fig.5 Stress-strain curves of UHPC（CA）under monotonic and fatigue loads

2.2.2 疲劳应变演化曲线

疲劳应变随循环比n/N（n为当前循环次数，N为疲劳寿命）的变化曲线为疲劳应变演化曲线.利用疲劳应变演化曲线来表征疲劳荷载作用下UHPC（CA）试件的变形发展规律，见图6.由图6可见，与FRC类似，UHPC（CA）的疲劳变形发展呈现明显的三阶段特征.

2.3 基于疲劳应变演化曲线的疲劳破坏过程分析

将疲劳应变演化曲线（见图6）划分为3个阶段，以反映UHPC（CA）的疲劳破坏全过程，如图7所示.

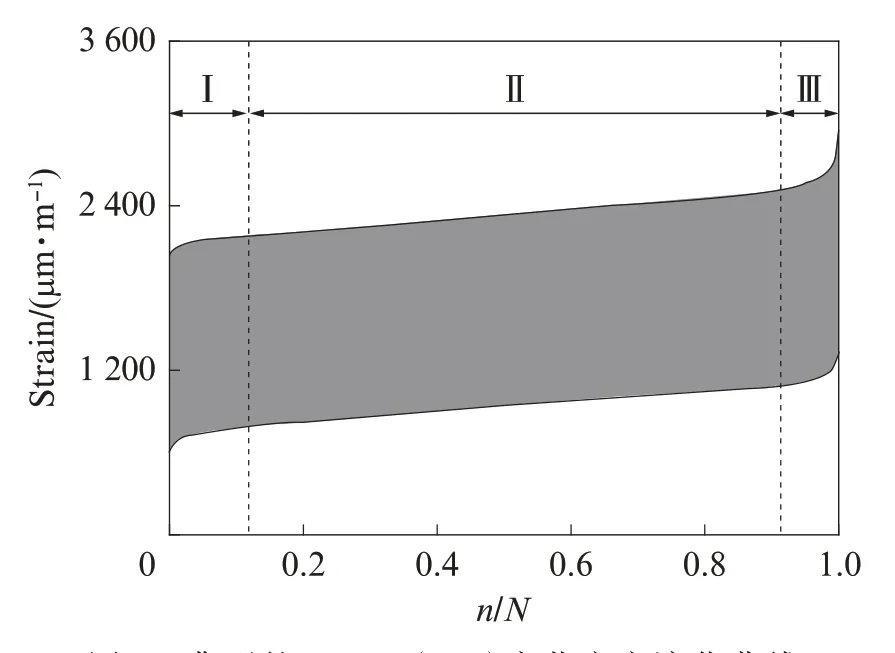
图6 典型的UHPC（CA）疲劳应变演化曲线Fig.6 Typical fatigue strain evolution curve of UHPC（CA）

（1）第Ⅰ阶段——微裂纹萌生发展阶段（见图7中A→B）.此时初始微孔洞在疲劳荷载作用下开始发展.钢纤维与UHPC基体之间的界面最初是完整的，并在这一阶段结合在一起，但纤维增强效果不明显.通过UHPC（CA）的纳米压痕试验发现，粗骨料-基体界面过渡区是其力学性能薄弱环节［7］.因此，第Ⅰ阶段中UHPC（CA）的变形发展不仅有初始微孔洞的扩展，还包含界面过渡区等内部薄弱环节微裂纹的出现.该阶段末，试件表面混凝土开始出现小面积脱落，见图8（a）.

（2）第Ⅱ阶段——微裂纹稳定发展与宏观裂缝萌生阶段（见图7中B→C）.此时初始微孔洞和界面过渡区的裂纹缓慢扩展.内部微裂纹穿过钢纤维，钢纤维开始发挥阻裂作用.主要表现为试件的应变以接近恒定的速率缓慢增长，伴随疲劳荷载的施加，试件表面继续脱落.第Ⅱ阶段中后期，可以观察到试件中的宏观裂缝，见图8（b）.

（3）第Ⅲ阶段——宏观裂缝发展阶段（见图7中C→D）.试件出现宏观裂缝后，钢纤维发挥了重要的桥接作用.随着越来越多的裂纹穿过纤维，钢纤维以化学黏结和摩擦的形式承受作用于断裂面上的疲劳荷载.对比图8（b）、（c）可以发现，试件疲劳破坏前，宏观裂缝并没有非常明显的发展，这表明钢纤维有效限制了宏观裂缝的发展.随后，试件迅速发生疲劳破坏.

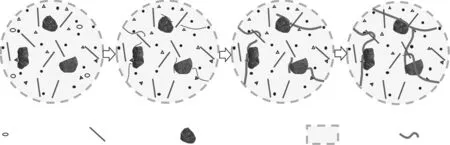
图7 UHPC（CA）的微观破坏过程Fig.7 Microscopic failure process of UHPC（CA）

图8 UHPC（CA）的宏观破坏过程Fig.8 Macroscopic failure process of UHPC（CA）

2.4 疲劳方程及疲劳强度

2.4.1 疲劳寿命概率分布

现有研究中，通常利用Weibull分布理论来研究混凝土疲劳寿命［5，10-11］.由于混凝土疲劳寿命离散性较大，为了保证疲劳寿命分布结果偏于安全可靠，本文采用双参数Weibull分布进行分析.

Weibull分布方程可简化为：

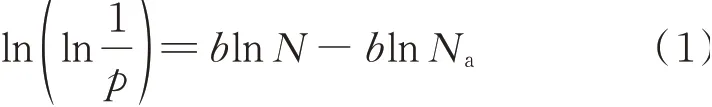
式中：p为存活率；N为疲劳寿命；Na为特征寿命参数；b为直线方程的斜率.

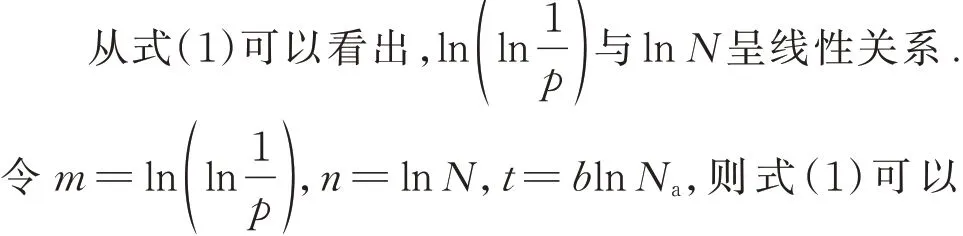
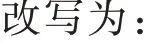
各应力水平下UHPC（CA）的疲劳寿命试验结果见表2（表中记有“*”的数字表示该试件在经受200万次疲劳荷载后仍未破坏，此时停止加载），其中存活率p的计算式为：

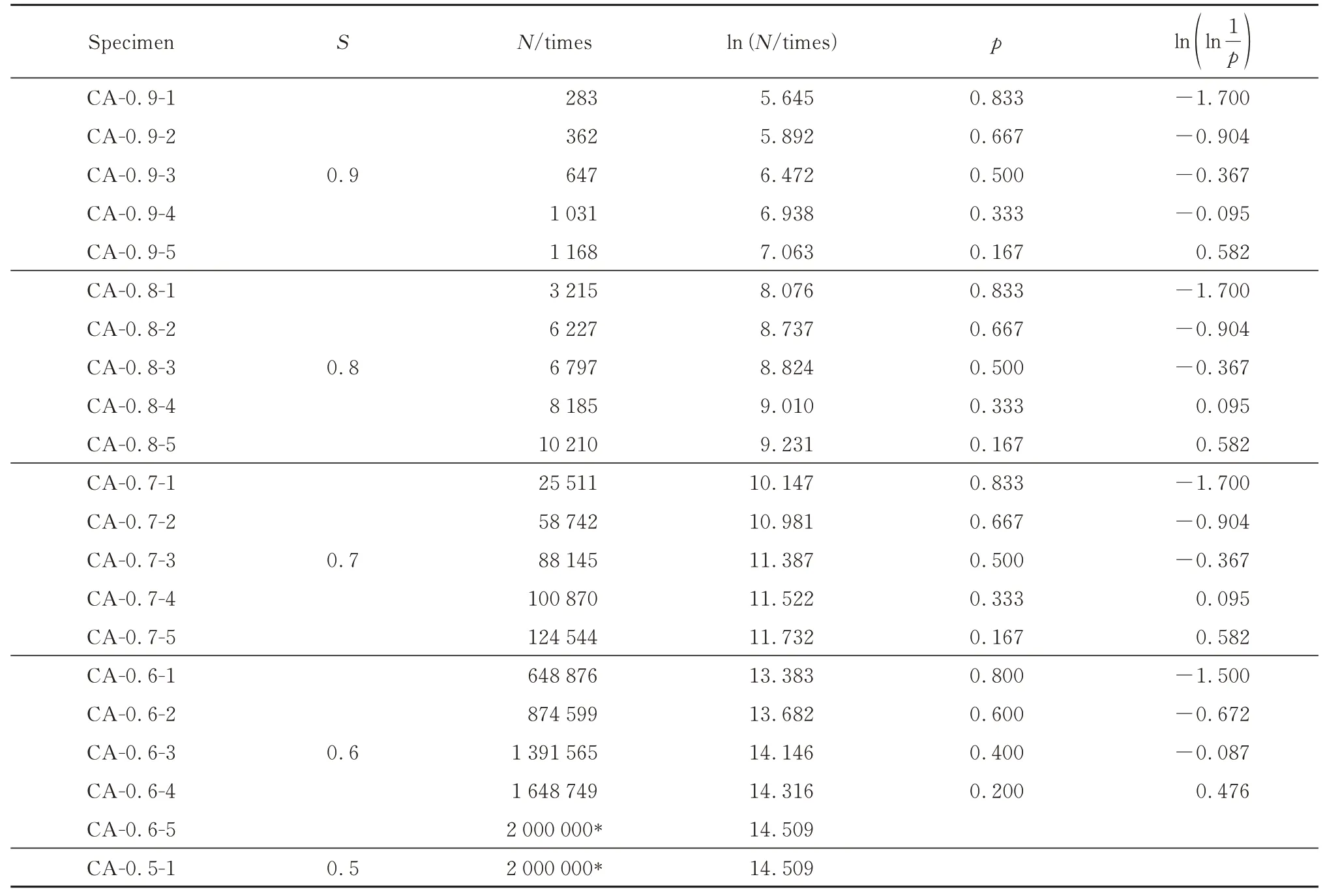
表2 疲劳寿命试验结果Table 2 Test results of fatigue life

式中：i为试件按疲劳寿命升序排列后的序号；k为样本容量.由图9可知，在各应力水平下的线性关系均较好（R2均大于0.9），说明Weibull分布可用于表征UHPC（CA）的单轴受压疲劳寿命.根据线性拟合表达式，求得各应力水平下疲劳寿命的Weibull分布参数b和Na，结果见表3.

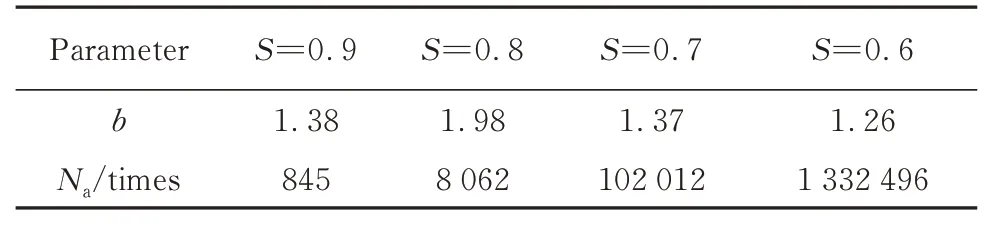
表3 UHPC（CA）单轴受压疲劳寿命的Weibull分布参数Table 3 Weibull distribution parameters of uniaxial compressive fatigue life of UHPC（CA）

2.4.2 考虑存活率的p-S-N疲劳方程

UHPC结构在疲劳设计时需考虑疲劳寿命和疲劳强度的离散性，因此，本节建立UHPC（CA）材料考虑存活率的p-S-N疲劳方程.式（4）为Weibull分布的失效概率（p′）方程.

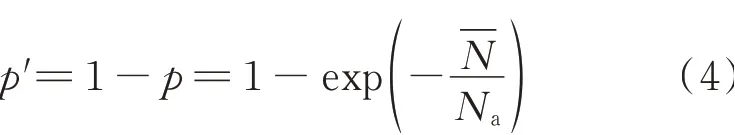
基于Weibull分布参数可得各失效概率下UHPC（CA）的等效疲劳寿命.将UHPC（CA）的等效疲劳寿命以双对数疲劳方程形式进行线性拟合，即可获得不同失效概率下的S-N方程，进而求得UHPC（CA）的疲劳强度.式（5）为UHPC（CA）的p-S-N疲劳方程.

将建立的p-S-N疲劳方程绘制于图10，可以发现本文受压疲劳寿命试验结果均落在0.05～0.95失效概率范围内.

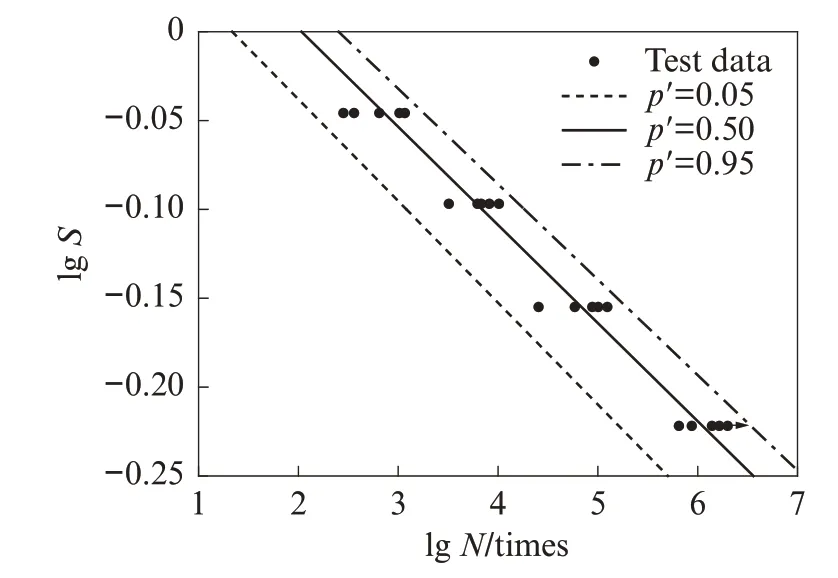
图10 UHPC（CA）疲劳寿命与p-S-N方程的关系Fig.10 Relationship between fatigue life and p-S-N equation of UHPC（CA）

2.4.3 疲劳强度

疲劳强度是指疲劳寿命N趋近无穷大时所施加的最大应力.混凝土材料的疲劳极限寿命通常取为200万次，由p-S-N疲劳方程可求出不同失效概率下UHPC（CA）疲劳强度对应的应力水平Sf，见表4.

表4 不同失效概率下UHPC（CA）疲劳强度对应的应力水平S fTable 4 Stress level S f corresponding to fatigue strength of UHPC（CA）under different failure probabilities

由表4可见，随着混凝土抗压强度的增大，其疲劳强度对应的应力水平Sf呈现减小的趋势.UHPC（CA）棱柱体试件的抗压强度为118.8 MPa，失效概率为0.05时，200万次疲劳寿命对应的应力水平为0.520，则具有95%存活率的UHPC（CA）疲劳强度为61.78 MPa（118.8×0.520）.