聚合物改性水泥浆体黏弹性的频率响应（I）：动态力学分析

张震雷， 史美伦， 杜 江

（1.同济大学 材料科学与工程学院，上海 201804；2.同济大学先进土木工程材料教育部重点实验室，上海 201804）

混凝土的应力-应变关系、徐变、干缩等力学性质一般在时域进行测量，时域测量的结果可以表示成应力-应变函数（一般是经验式），也可以进一步表示为本构关系或形象地表示为流变模型［1-3］.由于混凝土在应力下的应变很小，因此时域测量费时，且准确性较差.为了解决这一难题，本文应用动态力学分析（DMA）的频域方法，通过不同频率下的正弦波扫描，得到应力和应变在不同频率下的振幅及相位差，并换算成表征材料黏弹性的弹性模量（储能模量和损耗模量）.以储能模量为实轴、损耗模量为虚轴，得到材料的复平面图；储能模量和损耗模量组成复模量——松弛模量，其倒数称之为复柔量——徐变柔量.不同频率下，将试验得到的复模量或复柔量数据点集中在复平面上形成一条曲线，根据该曲线的形状和位置，可以确定混凝土作为黏弹性材料的流变模型，并以此为出发点得到模型参数，从而进一步得到混凝土的本构方程和力学信息.这种方法在电介质物理和电化学中颇为常用，称为复平面分析［4-5］.本文把该方法引入混凝土的黏弹性研究，旨在以简便的方法，了解混凝土的干缩和徐变特性，为混凝土配合比设计提供参考.为了简化试验和满足仪器的测试条件，文中用水泥浆体代替混凝土，其工作原理和试验结果具有普遍意义，可以用于一般混凝土.

1 理论简述

混凝土材料作为黏弹性材料，可视为弹簧和黏壶经串联和并联形成的组合，其组合方式可用流变模型来形象地表示［6-8］，如图1所示.

图1 流变模型Fig.1 Rheological models

图1中E1、E2为弹簧参数，η为黏壶参数.标准固体流变模型为Maxwell模型与Kelvin模型的结合.应用动态力学分析，对试样施加正弦波的力学信号，可以直接测得复弹性模量E*=E′+iE″，其中实部E′为储能模量，虚部E″为损耗模量.E′和E″都是正弦波信号频率的函数，通过对各种不同频率下E′和E″的分析，可以得到流变模型及其参数E1、E2和η.习惯上，可以把试验所得不同频率下的实部和虚部数据放在一张复平面图上，根据图形的形状进行分析，便可较容易地得到流变模型的参数.

对于标准固体流变模型［9］，习惯上，应用复模量的倒数复柔量D*=D′+iD″更方便一些.

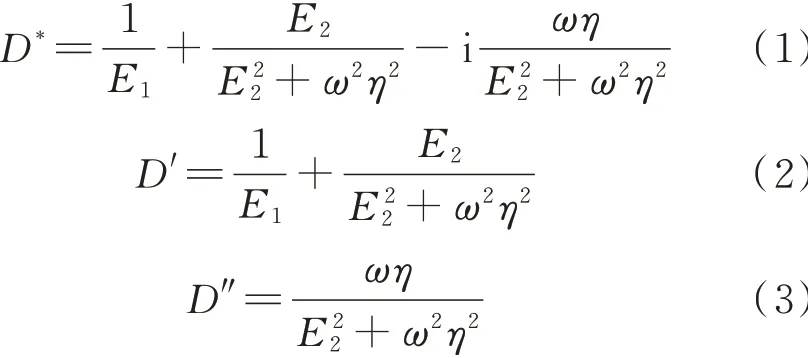
式中：ω为角频率，ω=2πf，其中f为试验频率.由式（2）、（3）可得：

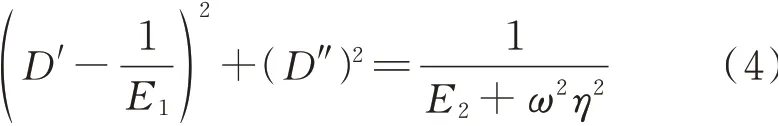
因此：

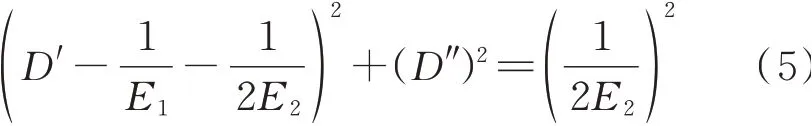
式（5）为圆的方程，是一个处于第1象限的半圆（如图2所示），直径处于实轴上，圆心坐标为从半圆与实轴的左交点可求得E1，右交点可求得E2.

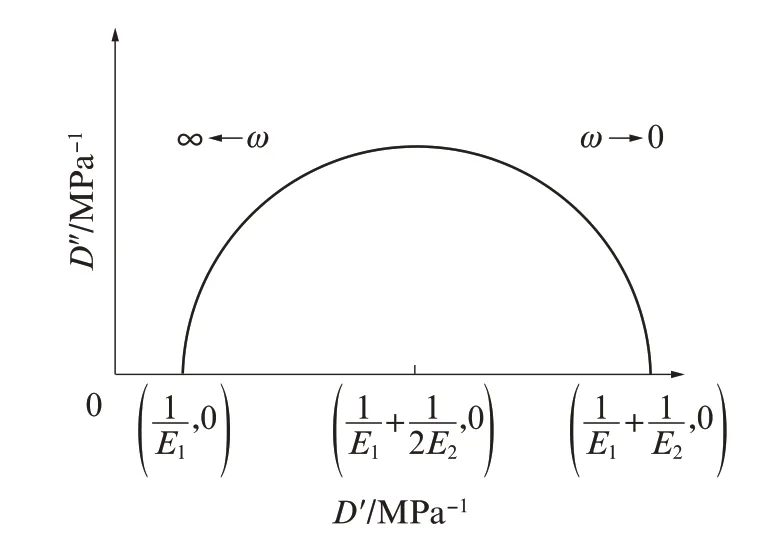
图2 标准固体流变模型复平面图Fig.2 Compliance of standard solid rheological model

2 试验部分

2.1 试验材料

水泥为中国联合水泥集团有限公司生产的P.I 42.5硅酸盐水泥.水泥的物理性能、化学组成1）文中涉及的组成、掺量、水灰比等均为质量分数或质量比.以及矿物组成如表1～3所示.

表1 水泥的物理性能Table 1 Physical properties of cement

聚合物选用德国Wacker公司生产的Vinnapas®5044N可再分散乳胶粉，该乳胶粉由乙烯/醋酸乙烯共聚物（EVA）组成，其基本物性参数如表4所示.

表4 EVA乳胶粉基本物性参数Table 4 Basic physical properties of EVA emulsion powder

表2 水泥的化学组成Table 2 Chemical composition of cement w/%

表3 水泥的矿物组成Table 3 Mineral composition of cement w/%

2.2 试样制备

EVA乳胶粉改性水泥浆体中水灰比固定为0.30，聚合物掺量分别为8%、12%、16%，对应的试样编号为PC-8、PC-12、PC-16.参照GB/T 1346—2001《水泥标准稠度用水量、凝结时间、安定性检验方法》，将按配合比混合好的原料在搅拌机上慢速搅拌120 s、停拌15 s、快搅120 s；然后把浆体装入钢模具中，试样尺寸为60 mm×13 mm×4 mm，振动成型；随即将试样在20℃、相对湿度（90±5）%的环境下养护24 h后脱模，然后置于20℃、相对湿度50%的空气环境中养护至28 d龄期［10］.

2.3 测试仪器及方法

采用美国TA公司生产的Q800动态力学分析仪（DMA）测试水泥浆体的黏弹性.测试在室温下进行，采用三点弯曲模式，预加力0.01 N，频率扫描范围0.01～100.00 Hz.

3 结果与讨论

3.1 二级标准固体流变模型的黏弹性复平面图

标准固体流变模型是黏弹性材料最简单的理想化流变模型［11-13］，实际上黏弹性材料的复平面图要比标准固体模型复杂得多.有时，由于测量频率范围的限制，只能出现半圆的一小部分，要根据半圆上3个以上的点来计算半圆的圆心和直径.大多数情况下，实际曲线是变了形的半圆、或呈压扁状，表现为几个相切或相割的半圆，这样的图形可以理解为“推广的标准固体流变模型”（见图3）.其中：图3（a）为二级标准固体流变模型，E0为串联弹簧参数，它与2个Kelvin元件相串联，E1、E2分别为2个Kelvin组件的弹簧参数，η1、η2分别为2个Kelvin元件的黏壶参数；图3（b）为上述二级标准固体流变模型发生交盖时的复平面图；图3（c）为存在多个相近特征时间的Kelvin元件串联时的复平面图，此时半圆呈压扁状.

3.2 推广的标准固体流变模型的复柔量表达式

标准固体流变模型的复柔量表达式可以简单地表示为：

复平面分析的优点是可以简单直观地从曲线来获得流变模型的参数.在上述复柔量图中：R0为原点到半圆与实轴左交点的距离；R1为半圆直径；T为半圆顶点频率ωp的倒数，见图3（b）.

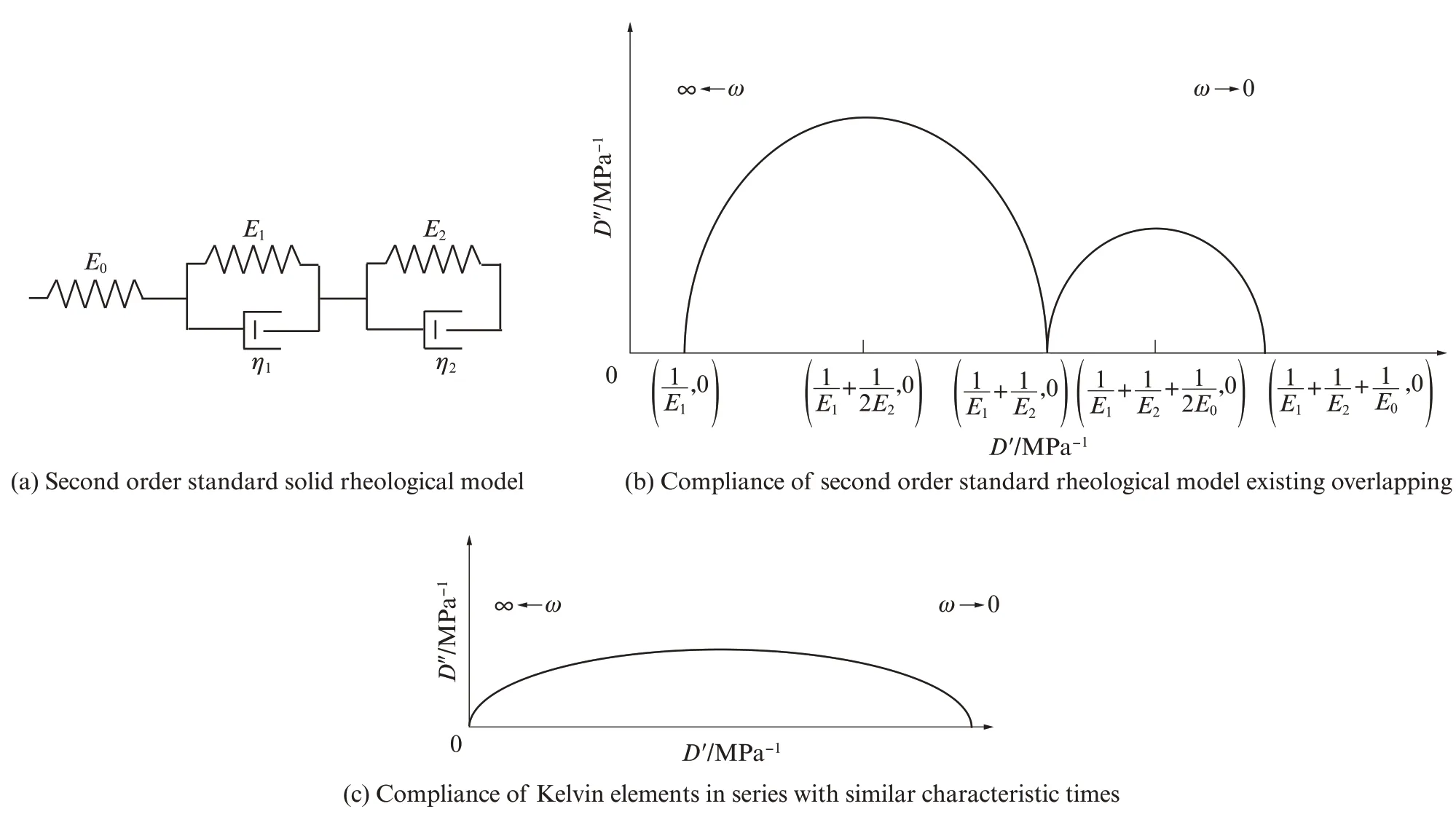
图3 推广的标准固体流变模型Fig.3 Generalized standard solid rheological models

对于推广的标准固体流变模型，则有：

由式（6）、（7）可得流变模型参数，以及由时域测量所得应力-应变关系与本构方程的相互联系［1-2］.

3.3 EVA改性聚合物水泥浆体的复柔量图及黏弹性参数

推广的标准固体流变模型中有几个R(1+iωT)项，就有几个不同的半圆顶点频率，其复平面图中就有几个相交或相切的半圆；复平面图中有几个半圆，就有几个不同的特征时间.如果特征时间T1、T2、…的数值比较接近，则这些半圆互相交盖，形成1个扁的圆弧，见图3（c）.反之，如果T1、T2、…相差较大，则在复平面上形成若干个分离的半圆.从每个半圆的位置和直径可以得到流变模型的参数Ri和T i，即从整个图形曲线可以直观地得出流变模型的全部参数.

图4为试样PC-8、PC-12和PC-16的复柔量图.由图4可见，试样PC-8、PC-12和PC-16的复柔量图都可以近似地认为由2个不完整的半圆组成，因此，聚合物改性水泥浆体的流变模型可以合理地假设为二级标准固体流变模型，或称为五参数模型.应用3点定圆法确定圆的半径和位置，得到的黏弹性参数如表5所示.

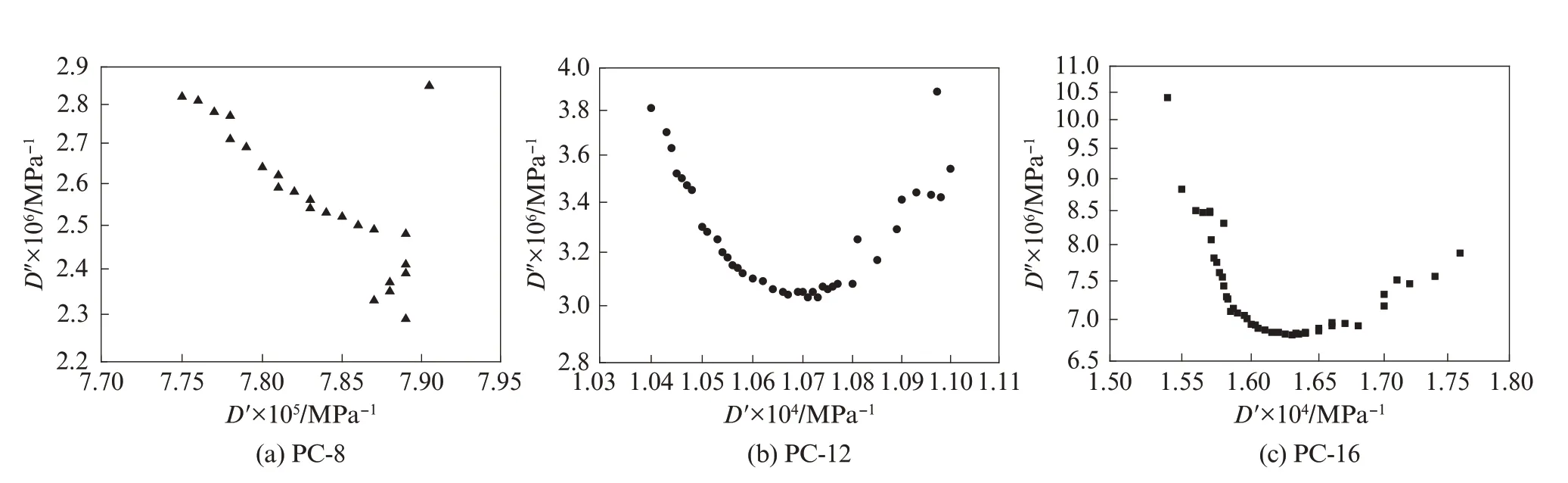
图4 试样PC-8、PC-12、PC-16的复柔量图Fig.4 Compliance of sample PC-8，PC-12，PC-16

表5中，ωp1和ωp2分别为2个半圆顶点的特征频率.由表5可见，随着水泥浆体中聚合物掺量的增加，E0变小，其他参数与聚合物掺量的相关性不明显.从本文应用动态力学分析的方法来估算聚合物改性水泥浆体黏弹性参数的具体例子来看，受测试频率范围的限制（只有4个数量级），得到的半圆不完整，对于参数估算的准确性有一定的影响.这一缺点可以通过复变函数的解析延拓，即通过K-K变换的方法来解决，笔者将在以后的文章里详细讨论.另外，从本文测得的试验结果来看，实际曲线和理论上应得的半圆有一定的差别，这是由于本文所用二级标准固体流变模型的近似性所致.实际材料应该是由无限个极小的Kelvin元件相串联，即相当于电路理论中所说的分布参数模型，其结果是图形的压扁或偏转，可以用常相角元件或分数阶导数来唯象地进行处理，笔者在文献［4-5，14］中已经进行了详细讨论.

表5 聚合物改性水泥浆体的黏弹性参数Table 5 Viscoelastic parameters of polymer modified paste

在对混凝土进行配合比设计时，通常主要考虑其强度和耐久性，而较少考虑其长期性能如干缩与徐变，对于干缩和徐变等混凝土黏弹性的问题，可用本文所建立的方法进行处理.

4 结论

（1）混凝土随时间变化的力学性质可以通过动态力学分析的方法在频域进行测量.频域测量的结果可以表示在复平面图上，根据复平面图上曲线的图形和位置，可以建立相应的流变模型，并估算其模型参数，从而了解其黏弹性.

（2）本文所用动态力学分析的方法可以对混凝土进行配合比设计，从而使其满足干缩和徐变等黏弹性要求.