水泥砂浆塑性收缩开裂预警机制拓展

2022-05-07马一平王琼琼朱文豪

建筑材料学报 2022年4期

马一平，王琼琼，付杰，朱文豪

（1.同济大学先进土木工程材料教育部重点实验室，上海 201804；2.上海空间电源研究所，上海 200245）

水泥基材料量大面广，是建筑物、道路及桥梁等工程中必不可少的组成部分.但因其自身原因，存在易收缩开裂的缺陷，会对水泥基材料的外观整体性、抗渗性、钢筋锈蚀性能等产生较大影响，大幅度降低结构物使用寿命.为此，国内外开展了大量研究：Menu等［1］基于力学理论，利用改进的圆环试验预测了喷射混凝土的收缩开裂敏感性；Boshoff等［2］提出了可预测混凝土塑性收缩开裂的模型，研究得出，减少水分蒸发速率、增加表面水分含量［3］均可有效缓解混凝土塑性收缩开裂.

但较少有学者将环境、材料组成、约束等施工条件纳入到水泥砂浆开裂预测中.鉴于此，笔者前期重点研究了水泥砂浆的干燥收缩开裂过程，在仅考虑环境变化的情况下初步建立了水泥砂浆塑性收缩开裂预警机制［4］.但实际施工时水泥砂浆还会受到材料组成、结构及约束等多方面的影响，因此，本文在前期研究基础上进一步拓展该预警机制：增加素砂浆与掺PVA纤维水泥砂浆本构方程中塑性收缩开裂的影响因素，扩大了环境参数的范围，进一步验证该预警机制的准确性及可行性.研究成果可为工程中准确预测水泥砂浆塑性收缩开裂提供方法，并有效预防开裂，为保障施工质量、提高结构物使用寿命贡献力量.

1 试验

1.1 试验原材料与仪器

水泥（C）采用上海产海螺牌P·O 42.5普通硅酸盐水泥，其化学组成1）文中涉及的组成、掺量和水胶比等除特别说明外均为质量分数或质量比.及物理力学性能同文献［5］；砂（S）采用天然河砂，细度模数2.59，粒径分布同文献［5］；缓凝剂采用玉堂牌普通食用白砂糖；减水剂（SP）采用湖南产雨虹牌聚羧酸减水剂；Ⅱ级粉煤灰（FA），比表面积341 m2/kg，粉末密度2.61 g/cm3；纤维采用福建产聚乙烯醇（PVA）纤维，其物理力学性能见表1；水（W）为实验室自来水.

表1 PVA纤维的物理力学性能Table 1 Physical and mechanical pr oper ties of PVA fiber s

试验仪器主要包括：JJ-5型水泥胶砂搅拌机；LTC-025-04型激光位移传感器；稠度测定仪；砂浆标准分层度桶；八字模；尺寸为914 mm×610 mm×20 mm的木模；电子天平，精度0.01 g；温湿度记录仪，温度精度0.3℃，湿度精度3%；SN-100型指针式拉压测力计，量程100 N，测量精度0.1 N；电子台秤，量程100 kg，精度0.01 kg.

1.2 试验方法

1.2.1 塑性收缩抗裂指数测试方法

水泥砂浆塑性收缩抗裂指数K为塑性抗拉强度与毛细管收缩应力的比值，是马一平等［6］早期提出的水泥砂浆塑性收缩开裂判据.塑性抗拉强度与毛细管收缩应力的具体测试方法见文献［6-7］.

1.2.2 失水蒸发速率测试方法

失水蒸发速率v是环境条件（温度、湿度、风速和光照）对水泥砂浆收缩影响的量化指标，应与毛细管收缩应力试验处于同一环境下测试，具体测试方法见文献［8］.

1.2.3 约束度的测试方法

约束度C是衡量水泥砂浆约束大小的指标，具体测试方法见文献［9］.实验室内水泥砂浆的约束度通过连接杆的直径进行调节，底部为硬化砂浆板时的约束度与连接杆直径为3 mm时的约束度（0.82）接近［9］.考虑到砂浆底部为硬化砂浆板的情况在工程中较为普遍，如用途较广的抹面砂浆，故本文将0.82定为常见情况下的约束度取值，即基准砂浆的约束度.基准砂浆指水胶比为0.50，砂灰比为1.00，约束度为0.82，分层度为1.00，减水剂、粉煤灰掺量均为0%的砂浆.下文基准砂浆参数同此处.

1.2.4 分层度的测试方法

分层度d是表征砂浆结构的参数.将砂浆标准分层度筒与砂浆放在同一底板上，用1 kg砝码敲击底板若干次，对筒中砂浆进行分层度测试，测试结果用来表征水泥砂浆的结构，具体测试方法见文献［9］.结论如下：不敲击时，砂浆分层度d=1.00 cm；敲击30下时，d=0.50 cm；敲击60下时，d=0 cm.

2 结果分析与讨论

2.1 素砂浆的七元本构方程

笔者前期初步建立的水泥砂浆塑性收缩开裂预警机制［4］仅考虑环境变化，构建了基于失水蒸发速率的素砂浆塑性收缩抗裂指数一元本构方程.该方程可准确预测不同环境下固定配合比的砂浆是否开裂，但当其他条件改变时，则无法进行预测.因此本节对方程的开裂影响因素进行扩充，建立了基于水胶比mW/mC、砂灰比mS/mC、失水蒸发速率v和粉煤灰掺量wFA、减水剂掺量wSP、分层度d及约束度C的素砂浆塑性收缩抗裂指数七元本构方程，试验数据见表2.

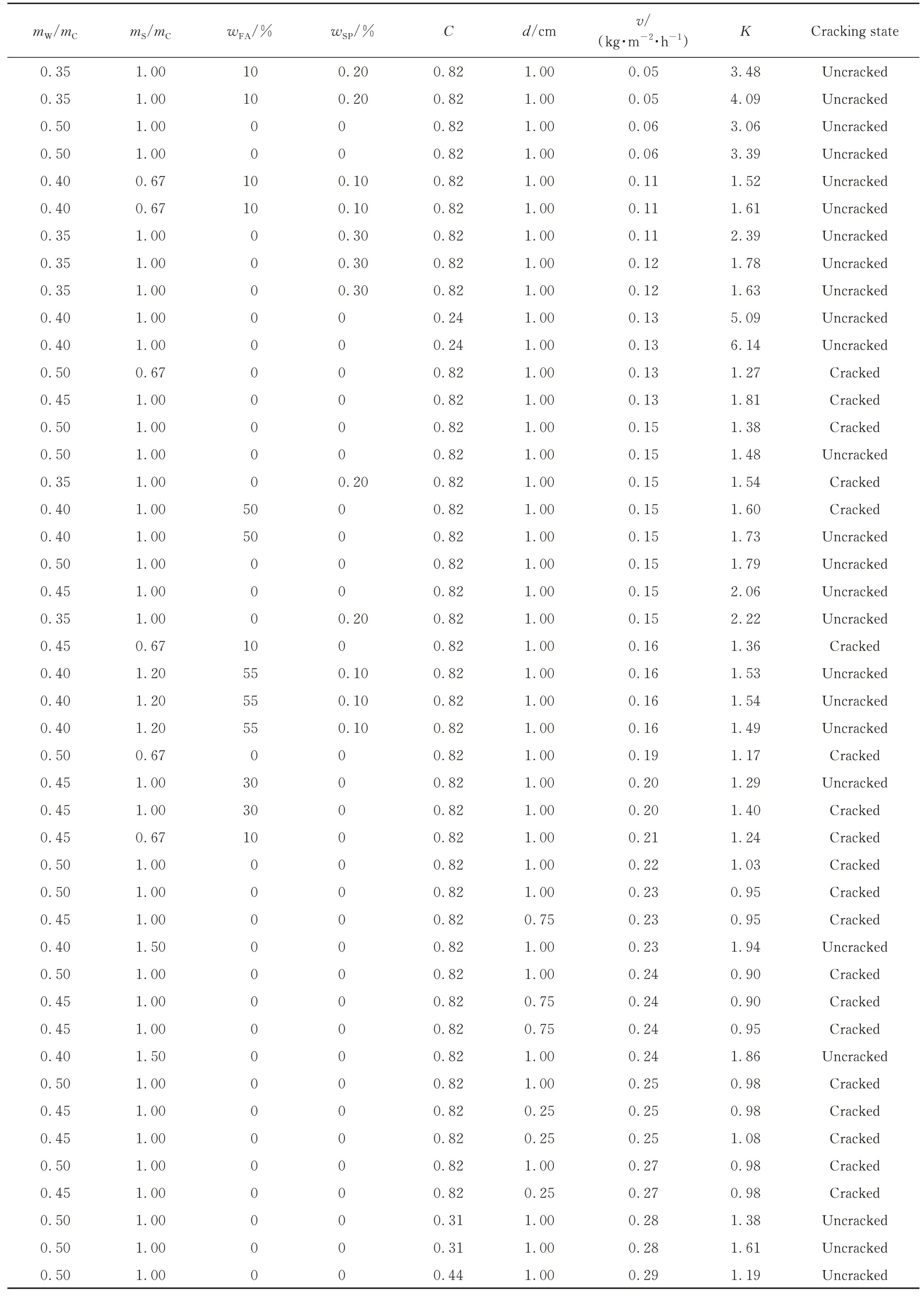
表2 素砂浆七元本构方程的试验数据Table 2 Experimental data of seven-element constitutive equation of plain cement mortar［10-11］

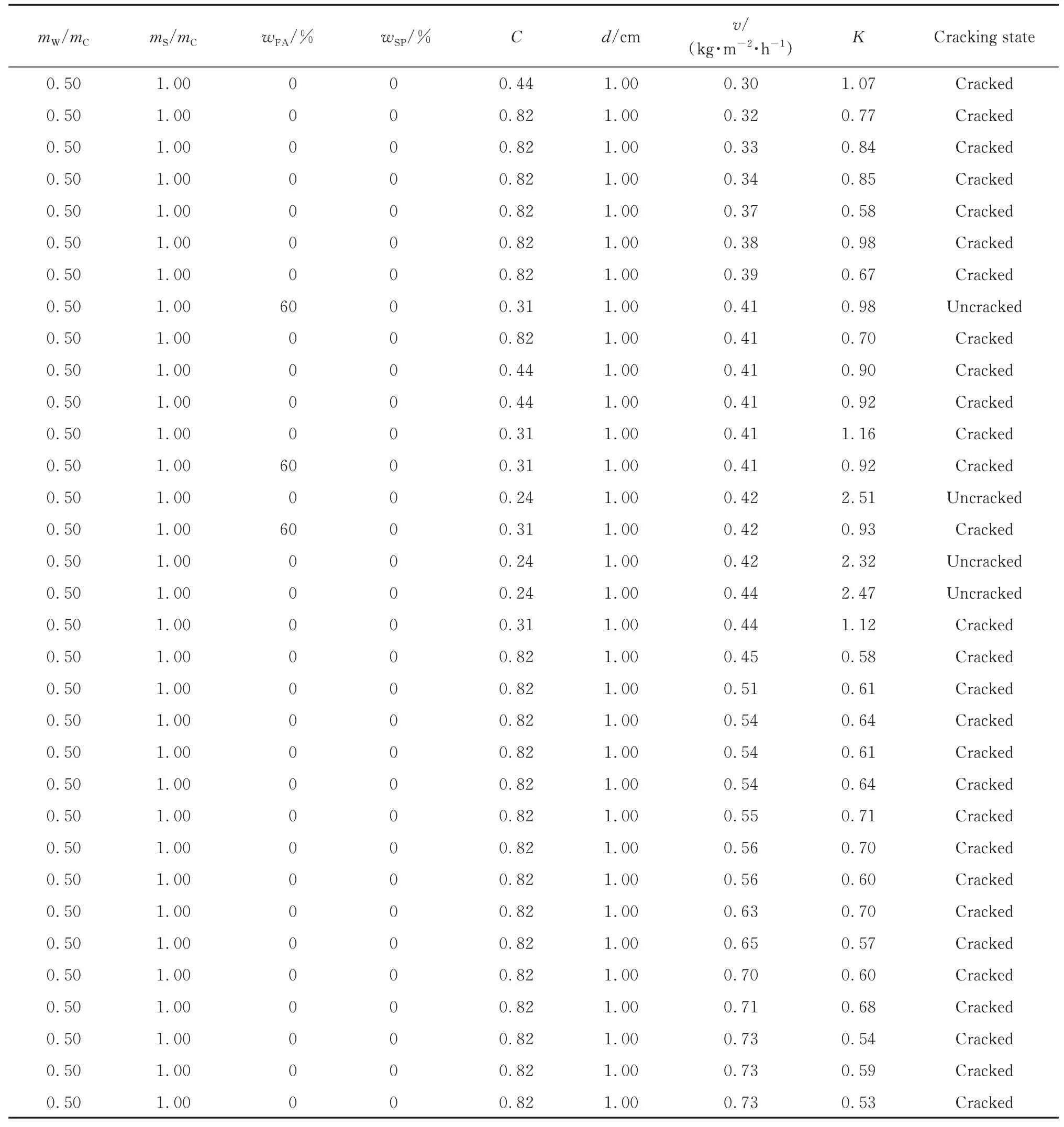
续表

本文尝试将表2中数据通过Excel进行多项式、Linest函数以及Logest函数拟合，最终选择相关系数最大的Logest函数进行回归分析，得到了适用范围更广的水泥砂浆塑性收缩抗裂指数的七元本构方程：

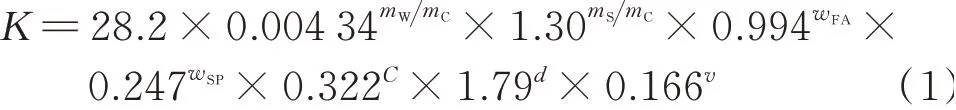
该方程的相关系数R=0.896，相关性明显.F统计量F=40.7.当显著性水平α=0.05时，从F分布表中查得临界值F0.05（7，70）=2.11，F＞F0.05（7，70），表明该七元本构方程整体显著性明显.各参数的显著性系数见表3.

由表3可知，七元本构方程中就单因素对水泥砂浆塑性收缩抗裂指数K的影响而言，v对K的影响最大.

表3 七元本构方程中各参数的显著性系数Table 3 Parameter significant coefficient of the seven-element constitutive equation

与笔者前期建立的素砂浆一元本构方程［4］相比：该七元本构方程拓展了水泥砂浆塑性收缩开裂影响因素，增加了mW/mC、mS/mC、wFA、wSP、d及C等参数，使预测方程更符合工程中复杂多变的情况，更具有实际意义；同时，环境参数v的上限由0.51 kg/（m2·h）扩大至0.73 kg/（m2·h），使预测方程更适用于天气极端的施工状况；另外，新方程所采用的数据点比前期建立的素砂浆一元本构方程更多.因此，新建立的七元本构方程可信度更高，适用范围更广，更具有实际工程意义.

将七元本构方程试验数据中不同条件下的K值与其对应的开裂状态归类于数轴中，得到本试验条件下水泥砂浆塑性收缩开裂的新判据，如图1所示.由图1可见：当K＜0.95时，砂浆开裂；当K＞1.86时，砂浆不开裂；当0.95≤K≤1.86时，砂浆以一定概率开裂.与前期建立的素砂浆一元本构方程的开裂判据节点1.08、1.79［4］相比，本次新判据的节点均向两侧扩张，因此概率开裂区间增大.由于本次建立的七元本构方程数据点多、范围大，因此所得新判据比前期判据更可信.

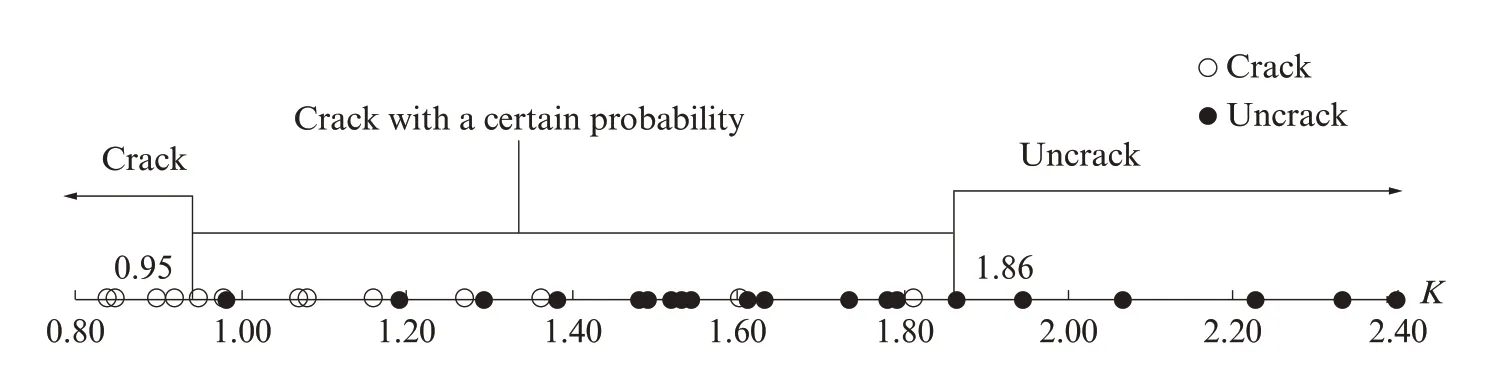
图1 七元本构方程的开裂判据（局部图）Fig.1 Cracking criterion of seven-element constitutive equation（partial enlarged view）

2.2 掺PVA纤维水泥砂浆的九元本构方程

在2.1的基础上，利用传统掺PVA纤维的方法进行减裂，通过调整纤维长度l与纤维质量浓度φ，测定掺PVA纤维水泥砂浆在不同条件下的抗裂指数，试验数据见表4.

表4 掺PVA纤维水泥砂浆九元本构方程试验数据Table 4 Experimental data of nine-element constitutive equation of cement mortar with PVA fibers［9，11］

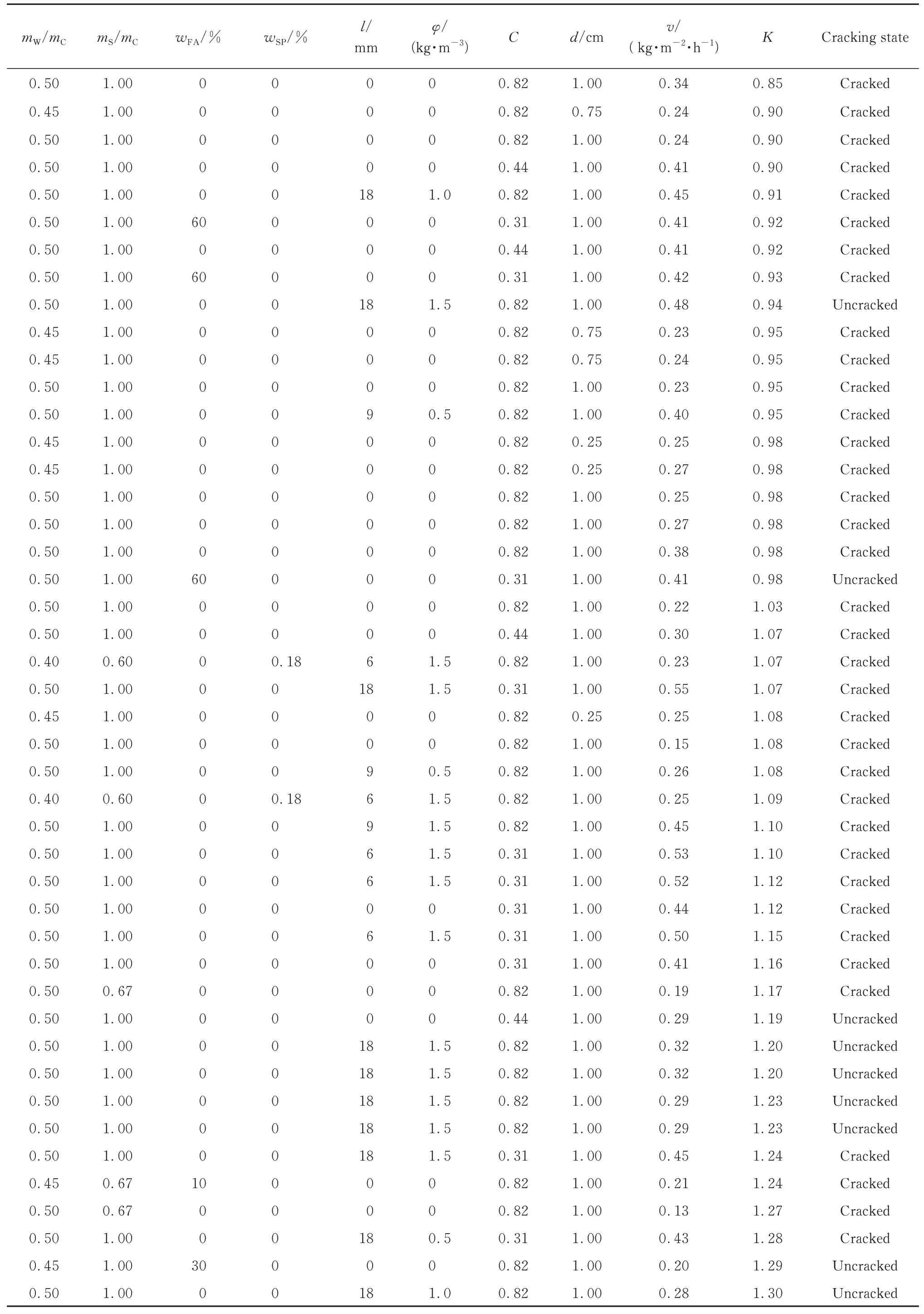
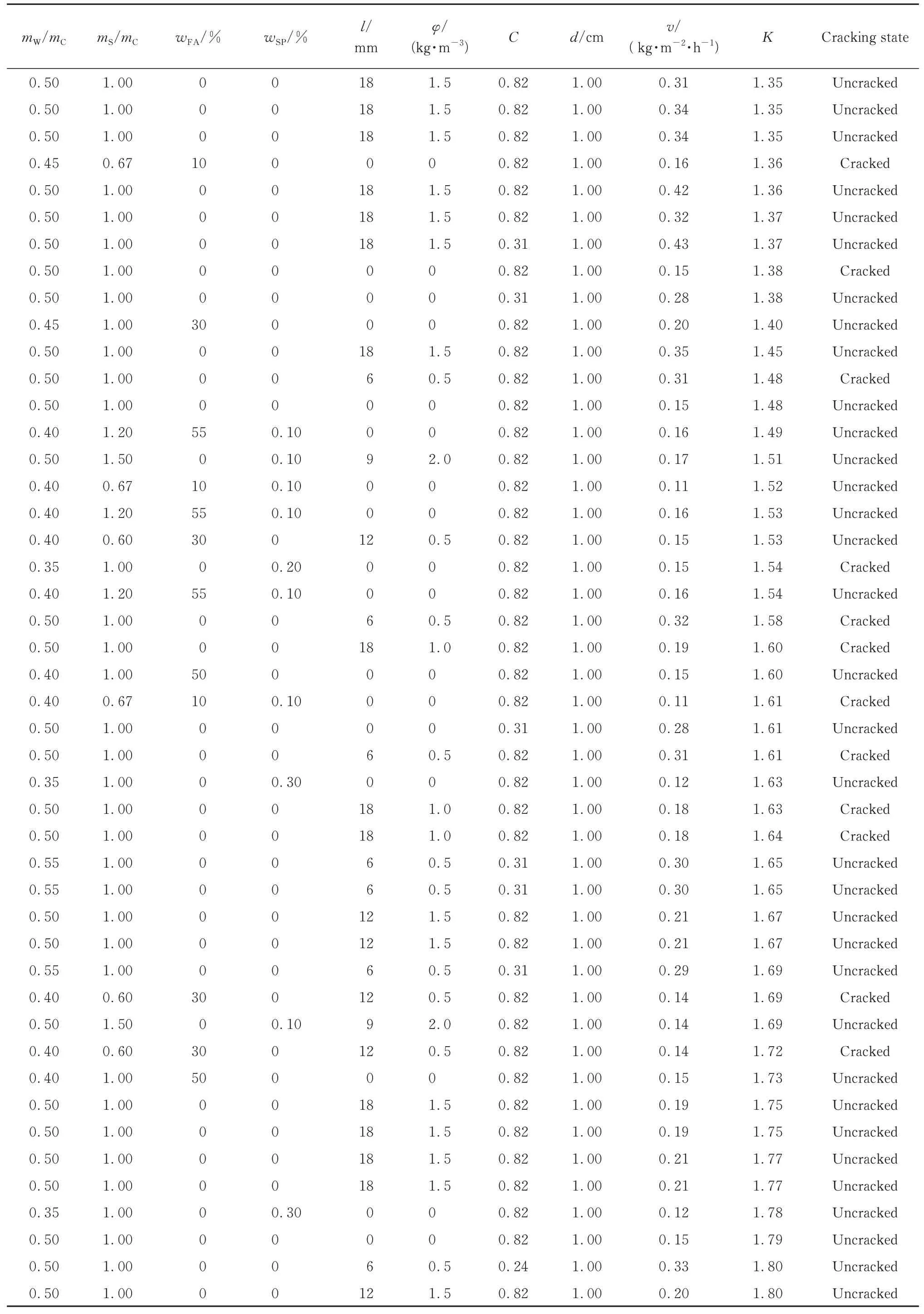
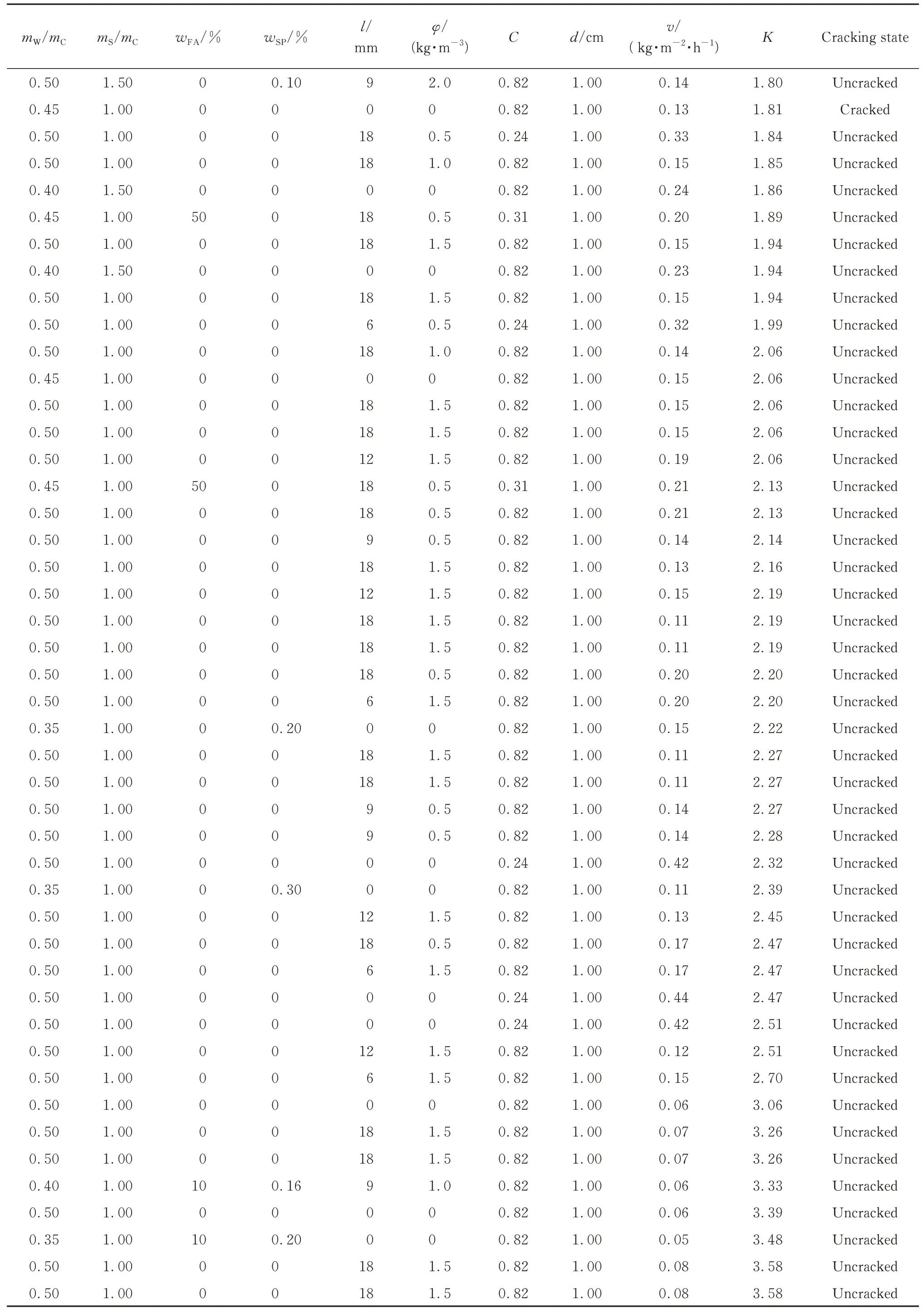
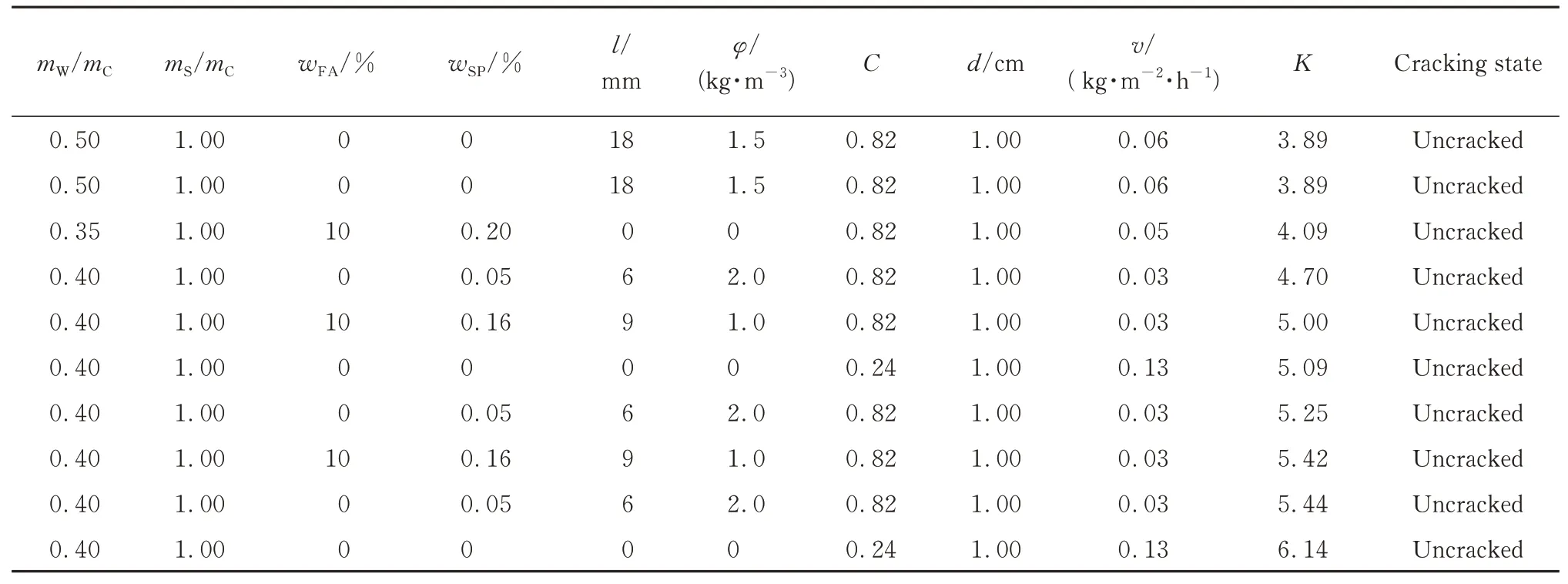
续表

利用Excel中Logest函数对表4中数据进行回归分析，得到掺PVA纤维水泥砂浆塑性收缩抗裂指数的九元本构方程：

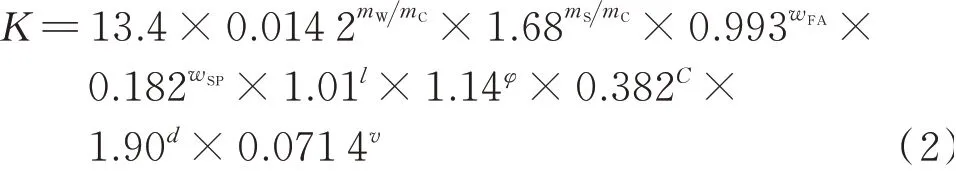
该方程相关系数R=0.894，相关性明显.F统计量F=71.1.在显著性水平α=0.05时，F0.05（9，160）=1.94，F＞F0.05（9，160），表明该方程整体显著性明显.九元本构方程中各因素的显著性系数见表5.

表5 九元本构方程中各参数的显著性系数Table 5 Parameter significant coefficient of the nine-element constitutive equation

结合表3、5可知，显著性系数绝对值较大的前3个变量（v、C、mW/mC）并未改变，说明就单因素而言，上述参数对K值影响较为明显.

与前面的七元本构方程类似，此九元本构方程比文献［4］中建立的掺PVA纤维水泥砂浆三元本构方程更具有可信度，更符合工程实际中复杂多变的情况，更满足实际施工条件.

将九元本构方程试验数据中抗裂指数与其对应的开裂状态归类于数轴中，可得到掺PVA纤维水泥砂浆塑性收缩开裂的新判据，见图2.由图2可见：当K＜0.93时，掺PVA纤维的水泥砂浆开裂；当K＞1.84时，砂浆不开裂；当0.93≤K≤1.84间，砂浆以一定概率开裂.与文献［4］中建立的掺PVA纤维水泥砂浆三元本构方程的开裂判据节点0.91，1.20相比，新判据节点皆增大，且不开裂区间的最小值增大较为明显，概率区间范围增大.由于新判据的样本点多、范围广，因此其可信度更高.

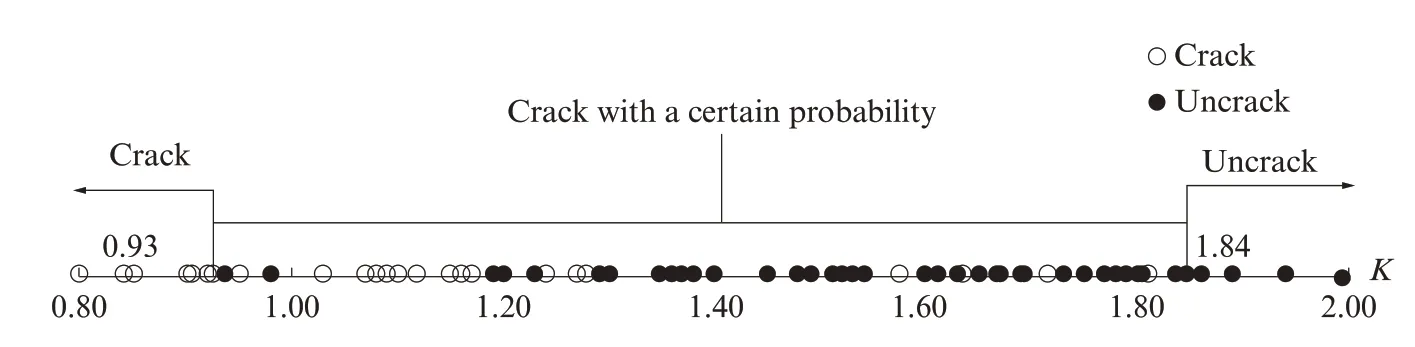
图2 九元本构方程的开裂判据（局部图）Fig.2 Cracking criterion of nine-element constitutive equation（partial enlarged view）

2.3 预警机制的拓展及验证

2.1和2.2已拓展建立了塑性收缩阶段预测素砂浆与掺PVA纤维水泥砂浆开裂状况的本构方程，将二者及其开裂判据结合，可建立新的水泥砂浆塑性收缩开裂预警机制，即：施工前使用式（1）对砂浆开裂状况进行预测，若K值在不开裂区间，则预测为不开裂，可直接进行施工；若预测为开裂，则可掺加PVA纤维进行减裂，再使用式（2）来验证掺PVA纤维水泥砂浆的开裂状况，若预测为不开裂，则说明PVA纤维减裂效果足够，可直接施工，若掺PVA纤维后预测仍为开裂，则调整纤维参数，再次用式（2）进行验证，直至预测为不开裂，方可施工.

为验证本文拓展的预警机制，笔者将前期初步建立的预警机制试验数据［4］代入本文预警机制中.其中，前期建立的三元本构方程只能改变v、l与φ这3个变量，mW/mC、mS/mC、wFA、wSP、d及C不可改变，后6个变量采用基准砂浆的取值参数（具体数据见上文）.将以上数据代入本文九元本构方程，结果见表6.

表6中试验1、2是室内试验.由试验1可知，在v=0.33 kg/（m2·h），其他变量为基准参数时，式（1）预测素砂浆K=0.94，小于素砂浆开裂判据中开裂最大值（0.95），预测砂浆开裂.实际砂浆试件确实开裂（K=0.97），与预测的状态相同，且预测K值相对于实测K值的误差为2.7%，小于15%，在可接受范围内（15%为水泥基材料研究领域一般可接受的变异范围）.说明本文方程的预测结果符合实际测量的结果，式（1）可准确预测该试验点的砂浆开裂状况.

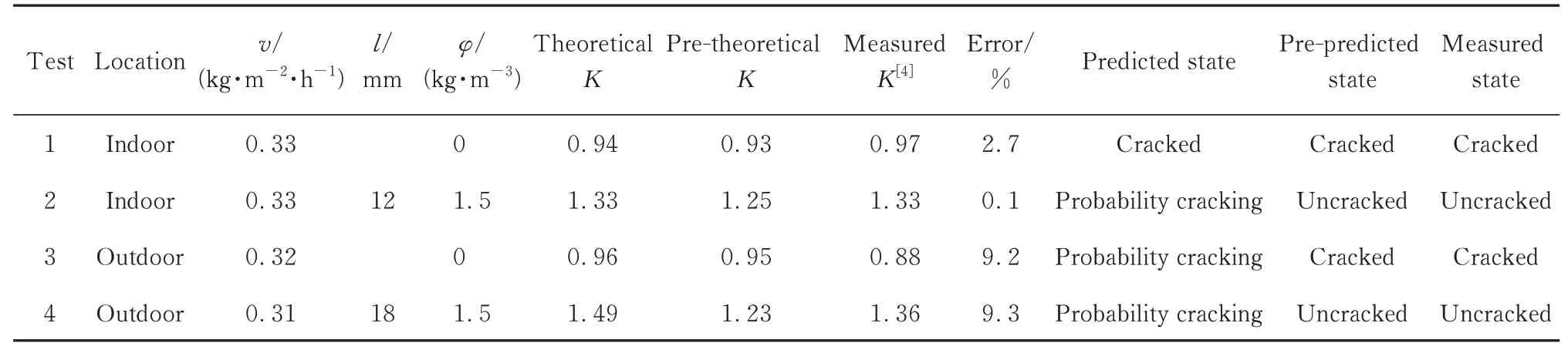
表6 前期数据在本文九元本构方程中的验证结果Table 6 Validation results of nine-element constitutive equation by pre-data

预测素砂浆在此条件下会开裂后，在同样的环境下掺加12 mm、1.5 kg/m3的PVA纤维进行减裂.将试验2的数据代入式（2），可得砂浆预测K值为1.33，处于九元本构方程开裂判据概率区间内，预测砂浆以一定概率开裂.实际测量结果砂浆未开裂，属于概率开裂的一种情形，且预测K值与实测K值相符，说明九元本构方程的预测结果符合砂浆实际测量结果，式（2）可在一定范围内准确有效地预测掺PVA纤维砂浆的开裂状况.本文九元本构方程预测K值1.33和前期三元本构方程预测K值1.25之间的相对误差仅为6.4%，但砂浆开裂的预测状态不一致，这主要是因为本文九元本构方程开裂判据的概率区间范围在前期基础上扩大较多，本文新判据更有效可信，故此次预测结果可信度较高.

上述试验1、2不仅证明了拓展预测方程式（1）与式（2）有效，同时也证明新预警机制在室内试验中科学可行：同样的环境下，用式（1）预测素砂浆在v=0.33 kg/（m2·h）时开裂；掺加12 mm、1.5 kg/m3的PVA纤维后，再用式（2）预测砂浆将以一定概率开裂，预测K值相对素砂浆提高了40.8%，且实际测量结果不开裂，表明掺PVA纤维后砂浆的抗裂效果比未掺时要好，拓展的新预警机制可在一定程度上预测并抑制砂浆开裂.但对于减裂要求高的工程，还需继续调整纤维参数，使预测K值处于不开裂区间方可施工.

上述结果显示新预警机制在室内确实科学可行，但考虑到实际施工时，试件多处于室外，比室内环境波动大，故本文将前期室外试验3、4的数据代入新预警机制中，验证其在实际施工条件下是否能较好地适用.与室内试验分析类似：预测素砂浆与掺PVA纤维水泥砂浆的开裂状况与实际状况皆相同，并且预测K值与实际K值的相对误差皆在可接受范围内，说明本文建立的素砂浆七元本构方程与掺PVA纤维水泥砂浆的九元本构方程在环境不稳定的室外也可较准确地预测砂浆开裂状况.同时，掺PVA纤维后水泥砂浆的预测K值相对素砂浆提高了54.7%，再次说明掺PVA纤维在该条件下的减裂效果较好，证明了在更符合实际施工的情况下新预警机制依然科学可行.

由以上对表6分析可知，本文新预警机制可包容并适用于前期试验结果.为再次验证新预警机制，笔者进行了2组室内、室外试验，其中每组素砂浆与掺PVA纤维水泥砂浆试验应同时进行，保证除纤维参数外其他变量皆相同，但考虑到v值不易控制，且v值相差较小时对PVA纤维的减裂效果影响有限，故试验中v值允许有较小偏差.试验中mS/mC、wFA、wSP、d及C仍取基准砂浆的取值参数（具体数据见上文），其余变量取值及验证结果如表7所示.

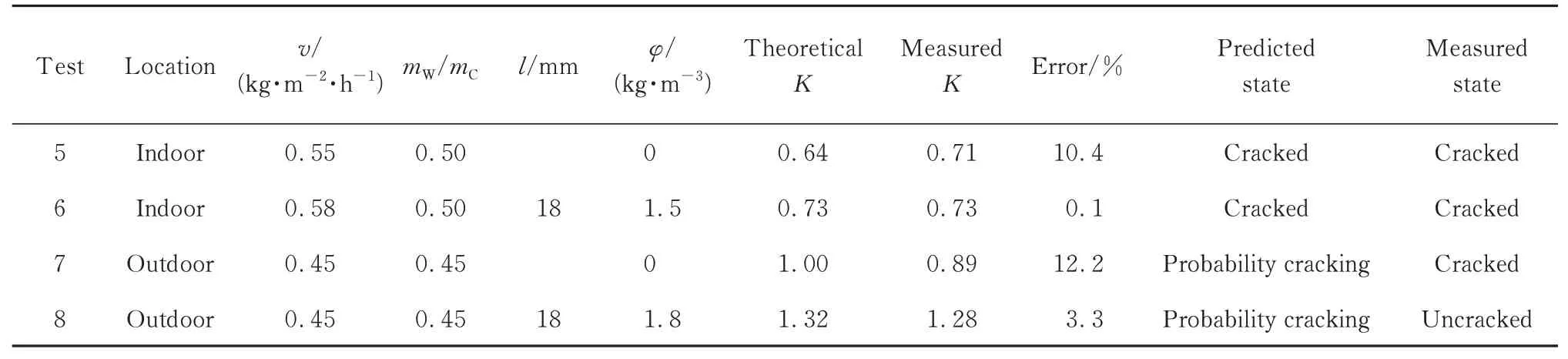
表7 室内室外验证试验数据Table 7 Experimental data of indoor and outdoor tests

与前期试验数据的分析类似，试验5、6的数据显示，素砂浆在v=0.55 kg/（m2·h）的室内情况下预测K值与实测K值相对误差在可接受范围内，预测砂浆开裂状态准确；然后在相似环境下掺PVA纤维进行减裂，方程预测情况与实际结果仍相符，再次证明本文拓展的预测方程可准确预测素砂浆与掺PVA纤维水泥砂浆是否开裂；同时，掺PVA纤维后砂浆的预测K值相对素砂浆提高了14.6%，证明了新预警机制预测与抑制开裂的思路是科学的，但若想确保施工质量还需继续调整纤维参数.试验7、8是在v=0.45 kg/（m2·h）的环境下进行的室外试验，将2次试验数据分别代入式（1）、（2）后的预测状况与实际测量结果均相同，且掺PVA纤维水泥砂浆的预测K值相对素砂浆提高了32.3%，实际试件不开裂，进一步证明了预测方程的准确性及新预警机制的科学可行性.

前期试验数据及笔者进行的试验结果多次证明了拓展的七元本构方程在mW/mC=0.35～0.50，mS/mC=0.67～1.50，wFA=0%～60%，wSP=0%～0.30%，C=0.24～0.82，d=0.25～1.00 cm，v=0.05～0.73 kg/（m2·h）的范围内可较准确预测素砂浆的塑性收缩开裂状况；拓展的九元本构方程在mW/mC=0.35～0.55，mS/mC=0.60～1.50，wFA=0%～60%，wSP=0%～0.30%，C=0.24～0.82，d=0.25～1.00 cm，v=0.03～0.67 kg/（m2·h），l=0～18 mm，φ=0～2.0 kg/m3的范围内可较准确地预测掺PVA纤维水泥砂浆的开裂状况.由于预测方程的拓展，新预警机制比前期初步建立的预警机制［4］更可信，使用范围更广，更符合施工中复杂的条件.并且，多次室内、室外试验证实，新预警机制可准确预测不同参数组合下的水泥砂浆开裂状态并有效减裂，保证工程具有较高的质量安全性及可靠性.