培育物理思想方法 提升推理论证能力

贵州 胡道成

2021年高考物理命题依托《中国高考评价体系》(以下简称高考评价体系)，切实体现了高考评价体系中“立德树人、服务选材、引导教学”的核心功能，强化基础性考查，优化情境设计，增强试题灵活性，深化关键能力考查，关注核心素养，培育物理思想方法，提升关键能力。现以几道“灵活性”很强的情境化试题为例，谈谈通过培育物理思想方法提升推理论证能力的备考策略，以期对2022年高考备考复习有所助益。

学生感到考查推理论证能力的题目难度较大的主要原因是这类问题的情境新颖，设问方式非常灵活，解决问题时需要创造性思维，甚至不乏需要依靠“直觉”来解决的问题，学生平时积累的解题经验已捉襟见肘！

解决这类问题依赖于物理观念指导下的物理思想方法的灵活运用。物理思想方法是在物理学发展过程中由物理学家们对物理知识、物理方法进一步概括而形成的关于物理学本质的深层认识。学生唯有将习得的知识和方法上升到物理思想的高度，才能切实提高自身解决问题的能力。“方法是通向能力的桥梁，能力既依赖于知识，更依赖于方法。在某种意义上方法本身是能力的一部分。能力培养可以从强化方法入手。”

推理论证能力是指学生能够根据已知的知识和物理事实、条件，通过归纳、演绎、类比等思维方式对物理问题进行推理和论证，从而得出正确的结论或做出正确的判断，并能把推理过程正确地表达出来。高考评价体系把“应用数学处理物理问题能力”也融入了“推理论证能力”之中，所以熟练运用数学工具也是培养推理论证能力的题中之意。

一、运用“对称思想”，寻找推理论证的依据

物理中的对称现象比比皆是，对称的作用、对称的结构、对称的电路、对称的物和像等等。对称通常表现为研究对象在结构上的对称性、物理过程在时间上和空间上的对称性、物理量在分布上的对称性及作用效果的对称性等。“对称”作为一种重要的思想和方法，在高考命题中随处可见，意在考查学生的直觉思维能力和猜想推理能力，引导教师在中学物理教学过程中注重培养学生的学科素养和美学素养。

【例1】如图1所示，四个电荷量均为q(q>0)的点电荷分别放置于菱形的四个顶点，其坐标分别为(4l，0)、(-4l，0)、(0，y0)、(0，-y0)，其中x轴上的两个点电荷位置固定，y轴上的两个点电荷可沿y轴对称移动(y0≠0)。下列说法正确的是

图1

( )

A.除无穷远处之外，菱形外部电场强度处处不为零

B.当y0取某值时，可使得菱形内部只存在两个电场强度为零的点

C.当y0=8l时，将一带负电的试探电荷由点(4l，5l)移至点(0，-3l)，静电力做正功

D.当y0=4l时，将一带负电的试探电荷放置在(l，l)处，其所受到的静电力方向与x轴正方向成45°倾斜向上

【答案】ACD

【解析】将x轴和y轴上的两个点电荷作为研究对象，显然它们连线的中点电场强度为0，同时考虑4个点电荷，菱形内部只有O点的电场强度为零；分析菱形外部则可以将4个电荷向O点集中视为一个正电荷，显然其周围的电场线是“光芒四射”的形状，电场强度除无穷远处之外处处不为零，选项A正确；根据对图2中电荷分布的对称性分析可知，无论y0取何值，菱形内部只有O点电场强度为零，选项B错误；根据对称性，可知点(0，-3l)与点(0，3l)关于x轴对称，两个点电势相等，所以将一带负电的试探电荷由点(4l，5l)移至点(0，-3l)，从静电力做功的视角来分析，完全可以视为移至点(0，3l)，此时若只考虑位于(0，8l)及(4l，0)这两个点电荷，从空间关系上看，其实点(4l，5l)与点(0，-3l)是关于两个点电荷连线对称的(见图2)，在这两个点电荷组成的电场中，移动负电荷的过程静电力做功为零，现在我们只需要考虑位于(-4l，0)和(0，-8l)这两个点电荷的静电力对负电荷的做功情况即可，显然上述移动过程中，负电荷靠近两个正电荷，静电力做正功，选项C正确；当y0=4l时，四个点电荷关于O点对称，将位于(-4l，0)、(0，-y0)和位于(0，y0)(4l，0)分别视为一对等量同种电荷，显然它们的合场强沿着与x轴正方向成45°倾斜的直线上，点(l，l)距离后面两个电荷较近，这里的场强方向沿直线倾斜向下，带负电的试探电荷放置在(l，l)处，其所受到的静电力方向与x轴正方向成45°倾斜向上，选项D正确。

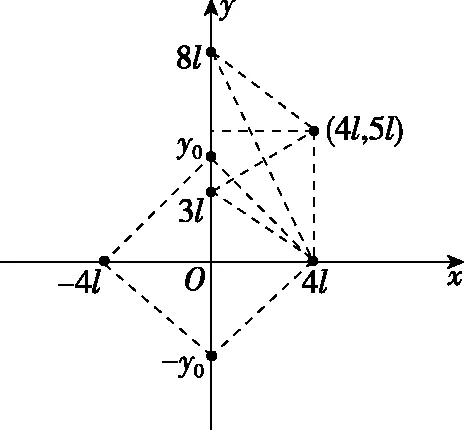
图2

【点评】本题自始至终围绕着寻找对称点来思考，回归到大家较为熟悉的“等量同种电荷”周围的电场分布情况，以便达到“以题攻题”的目的。将点(0，-3l)用(0，3l)来取代是一种能量观念，这样就能发现点(4l，5l)与点(0，-3l)是关于两个点电荷连线对称的，使推理论证过程“步步为营”，得出可靠的结论；将位于(-4l，0)、(0，-y0)和(0，y0)、(4l，0)的点电荷分别视为一对等量正电荷，也是因为这样看待问题容易与题给直线产生联系，使问题变得易于解决。通过这样的几次“辅助”处理，避免陷入复杂的数学计算，“难题”也就迎刃而解了。

二、运用“比较思想”，同中求异进行推理论证

比较是把事物的某些特征进行对比，以确定它们之间相同、不同或其他关系的思维活动过程，是一种确定客观事物之间差异和同一的抽象思维方法。解题过程中往往需要进行“同中求异”“异中求同”和“同异综合”的比较，其关键在于以相同去突破不同，所以就要善于以相同点作为比较的思维起点以找出表面上极为相似的事物之间在本质上的差异点。

【例2】(2021·全国甲卷·21)由相同材料的导线绕成边长相同的甲、乙两个正方形闭合线圈，两线圈的质量相等，但所用导线的横截面积不同，甲线圈的匝数是乙的 2倍。现两线圈在竖直平面内从同一高度同时由静止开始下落，一段时间后进入一方向垂直于纸面的匀强磁场区域，磁场的上边界水平，如图3所示。不计空气阻力，已知下落过程中线圈始终平行于纸面，上、下边保持水平。在线圈下边进入磁场后且上边进入磁场前，可能出现的是

图3

( )

A.甲和乙都加速运动

B.甲和乙都减速运动

C.甲加速运动，乙减速运动

D.甲减速运动，乙加速运动

【答案】AB

【点评】对于涉及力和运动的问题，一定要注意物体的运动情况是由其受力情况决定的，物体受力情况的分析才是判断现象是否发生或发生何种现象的依据，所以只有弄清受力情况，才能对形似而神异的运动过程进行分析，挖掘出题目中的隐含条件，要充分发挥“能量观念”和“运动与相互作用观念”对解题的指导作用，认真分析物体的运动过程，以找到适用的物理规律和相关公式进行推理论证，从而得出正确结论。本题的一大难点就是题给的情况具有很大的不确定性和开放性，需要先进行假设才能进行推理论证。增加问题的开放性是高考命题的新趋势，备考时应给予足够的重视。

三、运用“近似与估算”思想方法，基于“逼近”实现推理论证

灵活运用所学物理知识，依据与题目中的现象、过程相关的物理概念和规律，揭示题设条件与所求物理量之间的关系，运用物理方法和近似计算的方法，对所求物理量的数量级或物理量的取值范围进行大致地、合理地推理估算，从而得到合理的结果，这就是“近似与估算”思想方法。该思想方法要求学生在分析和解决问题时，要善于抓住主要因素，忽略次要因素，从而使问题得到简捷地解决。这类问题往往文句简洁、条件隐蔽，要从字里行间和附图中发掘隐含条件，寻找解题钥匙至关重要。

【例3】(2021·全国甲卷·18)2021年2月，执行我国火星探测任务的“天问一号”探测器在成功实施三次近火制动后，进入运行周期约为1.8×105s的椭圆形停泊轨道，轨道与火星表面的最近距离约为2.8×105m。已知火星半径约为3.4×106m，火星表面处自由落体的加速度大小约为3.7 m/s2，则“天问一号”的停泊轨道与火星表面的最远距离约为

( )

A.6×105m B.6×106m

C.6×107m D.6×108m

【答案】C

【点评】用“近似与估算”思想方法要充分发挥想象力和联想能力，根据基本概念和规律，把题目条件与结论通过基本公式联系起来，计算过程中要善于寻找与题给数据临近的、便于计算的数字来代替。平时也要有意熟记一些常用的近似关系，比如π2≈10；θ很小时，tanθ≈sinθ；当x≪1时，(1+x)n=nx+1之类。另外也要留意生活中的一些基本常识，比如楼层高度约为3 m；自行车速度约为4 m/s；鸡蛋质量约为50 g之类，以便遇到估算题时快速确定相关物理量的值，物理学来源于生活，我们没有理由不熟悉这个赖以生存的世界。

四、运用“假设思想”，以“讨论”的方式去推理论证

“一切科学都始于假说”，这句话高度概括了假说思想在物理学发展过程中的重要意义。而假设推理法是在假说思想指导下以科学事实为基础，对研究对象、物理过程、物理结论进行合理的假设，然后根据物理概念、规律等知识对具体问题进行比较、分析、综合、抽象、概括、计算、推理、讨论、判断，得到假设成立或不成立的结论，使问题得以解决的解题方法。熟练的运用假设法本身就是进行推理论证必须具备的关键能力。

【例4】(2021·河北普通高中学业水平选择性考试·9)如图4，矩形金属框MNQP竖直放置，其中MN、PQ足够长，且PQ杆光滑。一根轻弹簧一端固定在M点，另一端连接一个质量为m的小球，小球穿过PQ杆。金属框绕MN轴分别以角速度ω和ω′匀速转动时，小球均相对PQ杆静止，若ω′>ω，则与以ω匀速转动时相比，以ω′匀速转动时

图4

( )

A.小球的高度一定降低

B.弹簧弹力的大小一定不变

C.小球对杆压力的大小一定变大

D.小球所受合外力的大小一定变大

【答案】BD

【解析】设弹簧与水平方向的夹角为θ，设弹簧中的弹力大小为FT，因为PQ是光滑杆，弹簧一定处于拉伸状态，对小球进行受力分析，竖直方向受力平衡，有FTsinθ=mg①，水平方向做轨道半径r的圆周运动，设杆对小球的弹力为FN，则会出现三种可能性：(1)FN=0，此时FTcosθ=mω2r②；(2)FN方向水平向右，FTcosθ-FN=mω2r③；(3)FN方向水平向左，FTcosθ+FN=mω2r④。由①可知，假设ω增大到ω′，弹簧中的弹力FT增大，意味着弹簧形变量增大，小球下降，θ角将增大，sinθ也增大，显然这会导致①式不成立；弹簧中的弹力FT减小同样会导致①式不成立。所以弹簧中的弹力只能保持不变，小球的高度不会变化，选项A错误，B正确；因为FTcosθ是个定值，当FN=0时，ω为定值；当ω增大时，若为情况(2)，根据③式得FN减小，若为情况(3)，根据④式得FN增大，选项C是错误的；小球所受合外力F合=F向=mω2r会随着ω的增大而增大，选项D正确。

【点评】假设推理法在具体运用时，就是假设题目中具有某一条件，推得一个结论，将这个结论与实际情况对比，进行合理性判断，从而确定正确选项。假设条件的设置与合理性判断是解题的关键，因此要选择容易突破的点来设置条件，根据结论是否合理来判断假设是否成立。假设法在物理解题中的运用屡见不鲜。比如用假设法分析物体静摩擦力；用假设法判定物体受力情况；假设气体等温、等容、等压变化；假设某个临界条件……

总之，要提高推理论证能力就要善于引导学生独立地从具体的物理情境中获取信息，根据物理事实、条件，调用相应的物理概念、规律、模型，结合物理思想方法对问题进行逻辑推理和论证，才能得出正确的结论或做出正确的判断。培养学生的物理思想方法是形成物理观念、提高推理论证能力的有效途径。要让学生将习得的物理知识和物理方法上升到物理思想的高度，才能真正地达到盘活知识、技能、能力、思想方法的复习效果。

本文系2019年贵州教育科学规划立项课题“核心素养视域下高中学生物理能力培养的实践研究”(编号：2019B025)的阶段性成果。