几种特殊方法分析电场叠加类问题

贵州 胡朝平

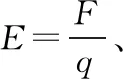
一、对称法

对称分析法就是利用物理现象、物理过程具有对称的特点来分析解决物理问题的方法。利用对称法求解电场强度就是利用空间上对称分布的电荷形成的电场具有对称性的特点，使复杂电场的叠加问题大大简化。

1.场源分段对称

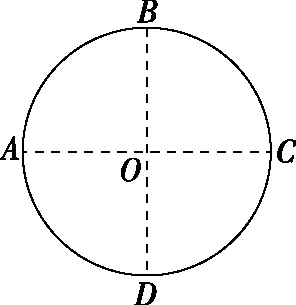
图1

( )

B.4E，方向由O指向D

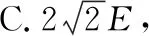
D.0

【答案】A

2.场空间对称

【例2】如图2所示，一半径为R的圆盘上均匀分布着电荷量为Q的电荷，在垂直于圆盘且过圆心c的轴线上有a、b、d三个点，a和b、b和c、c和d间的距离均为R，在a点处有一电荷量为q(q>0)的固定点电荷，已知b点处的场强为零，则d点处场强的大小为(k为静电力常量)

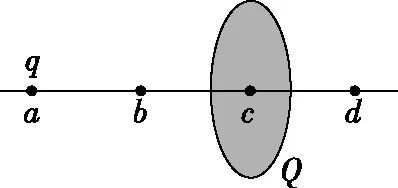
图2

( )

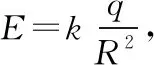
【答案】B

【评析】电场强度对称的两种形式：(1)结构的对称性，如均匀带电的圆环，在其圆心处产生的电场强度为零；(2)场的对称性，如等量同种、异种电荷形成的电场具有对称性。

对称现象普遍存在于各种物理现象和物理规律中，应用对称性能帮助我们认识和探索物质世界的某些基本规律，也能帮助我们去求解某些具体的物理问题，利用对称法分析、解决物理问题，可以避免复杂的数学演算和推导，直接抓住问题的实质，快速简便地求解问题。

二、等效法

在一些物理问题中，一个过程的发展、一个状态的确定，往往是由多个因素决定的，若某些因素所起的作用和另一些因素所起的作用相同，则这两个因素是等效的，它们便可以互相代替，而过程的发展或状态的确定对最后的结果并不影响，这种以等效为前提而使某些因素互相代替来研究问题的方法就是等效法。

【例3】如图3所示，在真空中某竖直平面内固定一足够大的接地金属板MN，在MN右侧与其相距2d处的P点放置一电荷量为Q的正点电荷，如果从P点作MN的垂线，则O为垂足，A为O、P连线的中点，B为OP延长线上的一点，PB=d。静电力常量为k，关于各点的电场强度，下列说法正确的是

图3

( )

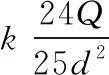
D.A、B两点场强大小相等，方向相反

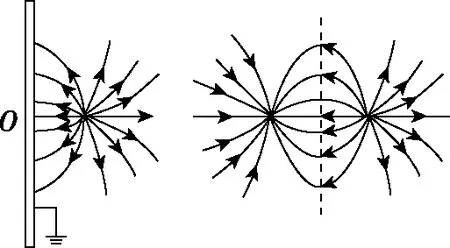
图4

【答案】AC

【评析】等效法的实质就是在效果相同的情况下，利用物理问题中某些相似或相同效果进行知识迁移，具体是指在效果相同的前提下，从A事实出发，用另外的B事实来代替，必要时再由B而C……直至实现所给问题的条件，从而建立与之相对应联系，再用有关规律解决。如以模型替代实物、以合力(合运动)替代数个分力(分运动)、等效电阻和等效电源等。常见的等效法有：(1)补偿法等效。求解物理问题时，要根据问题给出的条件建立起物理模型。但有时由题给条件建立的模型不是一个完整的模型，这时需要给原来的问题补充一些条件，组成一个完整的新模型。这样，求解原模型的问题就变为求解新模型与补充条件差值的问题。(2)类比法等效。在保证效果相同的前提下，将复杂的电场情境变换为简单的或熟悉的电场情境。

三、极限法

极限法是把某个物理量推向极端，即极大、极小、极左或极右，并依此做出科学的推理分析，从而给出判断或导出一般结论。

甲

( )

【答案】A

【评析】当某些问题无法求解时，可将某些物理量的值推向极端然后对选项进行分析推理，进而得出答案。解题时要注意：(1)有哪些量可以推向极端；(2)极端推向0还是无穷大。

极限法在进行某些物理过程的分析时，思路灵活，判断准确，具有独特作用。恰当应用极限法能有效提高解题效率，使问题化难为易，化繁为简。因此要求解题者，不仅要具有严谨的逻辑推理能力，还要具有丰富的想象力。

四、微元法

微元法就是将研究对象分割成无限多个微小的单元，取出有代表性的极小的一部分进行分析处理，再从局部到整体综合起来加以考虑的科学思维方法，在这个方法里充分体现了积分的思想。“微元法”是分析、解决物理问题的常用方法，它可以将非理想物理模型变成理想物理模型，然后利用必要的数学和物理方法处理“元过程”，从而解决问题。

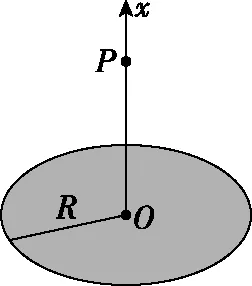
【例5】如图6所示，水平面上有一均匀带电圆环，所带电荷量为+Q，其圆心为O点。有一电荷量为+q、质量为m的小球恰能静止在O点上方的P点，O、P间距为L。P与圆环上任一点的连线与PO间的夹角都为θ，重力加速度为g，以下说法正确的是

图6

( )

A.P点场强方向竖直向上

图7

【答案】ABD

【评析】微元法可以使一些复杂的物理过程能够用我们熟悉的物理规律迅速地解决，使所求的问题简单化。在使用微元法处理问题时，将研究对象分解为很多“微元”或将其运动过程分解成许多微小的“元过程”(对应的物理量微元可以为时间微元、速度微元、位移微元、电荷量微元等)，分析每个“元过程”遵循的物理规律，然后将每个“元过程”相关的物理量累加求和，用必要的数学方法或物理思想处理，从而使问题得到解决。如将带电体分成许多微元电荷，每个微元电荷看成点电荷，先根据库仑定律求出每个微元电荷的电场强度，再结合对称性和电场强度叠加原理求出合电场强度。使用微元法能够加强我们对已知规律的再思考，从而起到巩固知识、加深认识和提高能力的作用。

五、综合运用

【例6】如图8所示，边长为L的正六边形ABCDEF的5条边上分别放置5根长度也为L的相同绝缘细棒，每根细棒均匀带上正电。现将电荷量为+Q的点电荷置于BC中点，此时正六边形几何中心O点的场强为零。若移走+Q及AB边上的细棒，则O点电场强度大小为(k为静电力常量，不考虑绝缘棒及+Q之间的相互影响)

图8

( )

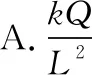
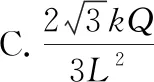
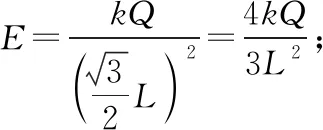
图9

【答案】D

总结：对于比较复杂的情况，运用多种方法综合分析，是我们在处理实际问题中常运用的方法。综上情况可知，在处理带电圆环、带电平面、带电球面等一些特殊带电体产生的场强时，如果转换思维角度，灵活运用对称法、补偿法、极限法、微元法、等效法等巧妙方法，就可化难为易，快速求解。