一种分解运动的新方法
2022-05-07山西景小娟
山西 景小娟
运动的合成与分解是高中物理重要的思想方法之一,是把疑难问题化繁为简的主要途径。《普通高中物理程标准(2017年版2020年修订)》中明确提出要求:“会用运动的合成和分解的方法分析曲线运动。体会将复杂运动分解为简单运动的物理思想。”而运动的合成和分解体现了“等效替代”的物理思维,本身就具有抽象性和复杂性,学生理解和接受起来具有一定的难度。
在中学阶段,一般都把曲线运动分解为两个相互垂直方向上的直线运动来研究。比如把平抛运动分解为水平方向上的匀速直线运动和竖直方向上的自由落体运动;把带电粒子在磁场中的螺旋线运动分解为一个平面上的匀速圆周运动和垂直这个平面方向上的匀速直线运动。但是如果物体运动的轨迹更加复杂一些,不存在上述明显的分解特征时,处理起来可能就较为棘手。那么,让我们拓宽思路,把分解的思想拔高并融入具体题目,把速度、加速度、力这些矢量进行另类的等效分解,巧妙的重新组合,就会形成令人耳目一新的分运动形式,进而解出在常规的正交分解情况下无法解得或难以解得的题目。本文就几道例题从不同的角度进行巧分解、妙解题。
【例1】如图1所示,轻绳一端系于O点,另一端系一金属小球,将小球拉至悬绳位于水平伸直状态时,由静止释放小球,问:小球在摆向最低点的过程中,所受重力的瞬时功率何处最大?
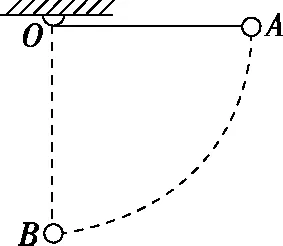
图1
【分析】本题的常规出题方式是让学生确定重力的瞬时功率从位置A到位置B过程中怎么变化,根据A处速度为0,所以A处的重力的瞬时功率为0;B处重力的方向和速度的方向垂直,所以B处的重力瞬时功率也为0,所以重力的瞬时功率先增加后减少。
但是题目稍作变化,要求学生做定量分析,求出重力的瞬时功率何处最大,则难度倍增。普遍采用的方法是数学方法,即写出重力瞬时功率的函数表达式,然后对t求导即可。
然而若是有了分解运动的思维,本题就可迎刃而解,且也没有很大的数学运算量。
解:设小球质量为m,绳长为l,取A至B间任意位置,绳与水平方向夹角为θ,此时瞬时速度为v。

此时重力的瞬时功率为P=mgvcosθ

若把小球的运动按水平方向和竖直方向进行分解,在竖直方向上,当合力为0,即竖直分加速度为0时,竖直分速度vcosθ就有最大值,则此时P就最大。如图2所示。
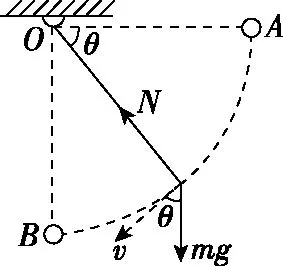
图2
可得N=3mgsinθ
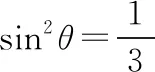

【点评】本题中对小球的运动做了两次正交分解,一次是沿轨迹径向和切向分解,另一次是沿水平和竖直方向分解,在自由切换中,明晰了物理情境,化繁为简。后面依然会涉及在同一个物理情境中作两次或两次以上的不同方向上的分解的问题。
【例2】如图3所示,空间存在一个范围足够大的垂直纸面向外的匀强磁场,磁感应强度为B,磁场中一质量为m、带电量为q(q<0)的小球(小球可看作质点),从高为h处以竖直向下的速度v0抛出,若小球恰好不会与地面相碰,且运动过程中的最大速度为vm,以下关系式正确的是

图3
( )
【分析】当带电粒子在正交的匀强磁场和匀强电场(或重力场)所形成的复合场中运动时,若所受的洛伦兹力与电场力(或重力)不平衡,电场力(或重力)会改变粒子的速度,而速度的变化又会使洛伦兹力不断改变,使粒子做复杂的曲线运动,常规方法难以解决此类问题。针对这类问题,通常采用“配速法”即给带电粒子配上一对等大反向的速度或者分解初速度,使其中一个速度对应的洛伦兹力与电场力(或重力)平衡,则该速度对应的分运动就是匀速直线运动;另一速度和对应的洛伦兹力构成另一分运动——匀速圆周运动,这样就可将复杂的曲线运动分解为简单的匀速直线运动和匀速圆周运动。


图4
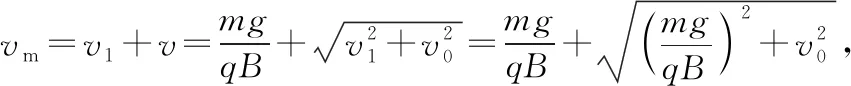
【例3】某位工人师傅用如图5所示的装置,将重物从地面沿竖直方向拉到楼上,在此过程中,工人师傅沿地面以速度v向右做匀速直线运动,当质量为m的重物上升高度为h时轻绳与水平方向成α角(重力加速度大小为g,滑轮的质量和摩擦均不计),在此过程中,下列说法正确的是
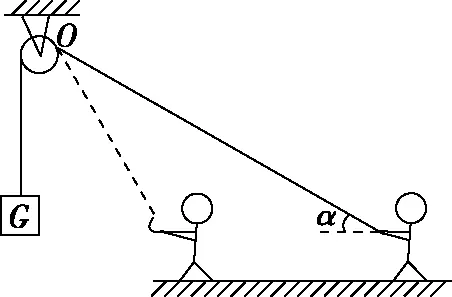
图5
( )
A.人的速度比重物的速度小
B.轻绳对重物的拉力小于重物的重力
C.重物的加速度不断增大
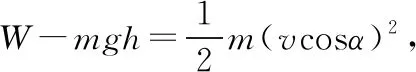
C选项的判断相对麻烦些,可以用下面几种方法。例如趋于极限法,当人在匀速向右运动过程中,α是不断减小的,当α趋近于0时,vG无限接近于v,速度增加的越来越慢,所以加速度减小,则C错误;也可以利用数学微分的方法,将vG对时间t求导,即可解出重物加速度的表达式,得出结果,此处不再详细解答。


图6
【点评】本题巧妙利用运动的分解轻松地算出重物的加速度,避免了数学微分法繁复的计算过程,不失为一种捷径。
【例4】如图7所示,劲度系数为100 N/m的轻弹簧下端固定于倾角θ=53°的光滑斜面底端,上端连接物块Q,Q同时与平行于斜面的轻绳相连,轻绳跨过定滑轮O与套在光滑竖直杆的物块P连接,图中O、B两点等高,间距d=0.3 m。初始时在外力作用下,P在A点静止不动,A、B间距离h=0.4 m,此时轻绳中张力大小为50 N。已知P质量为0.8 kg,Q质量为5 kg。现将P由静止释放(不计滑轮大小及摩擦,取g=10 m/s2,sin53°=0.8,cos53°=0.6),下列说法正确的是

图7
( )
A.P上升至B点时,弹簧的压缩量为0.2 m
B.P由静止释放的瞬间,绳的拉力为50 N;P上升至B点时,绳的拉力为30 N
C.P上升至B点的过程中,Q的加速度先增大后减小
D.P上升至B点的过程中,轻绳拉力对其所做的功为8 J
【解析】本题中AD选项是比较容易判断的。由题意知,初始状态时,弹簧处于拉伸状态,由平衡条件可得弹簧拉力为T=kx0+mgsinθ,T=50 N,则x0=0.1 m;当P上升至B点到达末状态时,因为绳子不可伸缩,Q下降Δx=0.2 m,所以此时弹簧是压缩状态,压缩量为x=0.1 m,A错误。

仅对B、C做出正误判断还是比较简单的,通过逻辑推理和定性分析就可以。由题意可知,Q初末状态速度都是0,所以Q沿斜面方向先做向下的加速度减小的加速运动,后做加速度增大的减速运动,所以Q的加速度先减小后增大,C错。P物块释放瞬间和到达B点瞬间,沿绳方向上的加速度都不可能是0,而B选项中的数据即绳的拉力 50 N 和30 N很显然都是按照Q处于平衡状态计算出来的,所以一定是错误的,B错误。
但是如果想要更加准确的计算出运动过程中绳的拉力及两物块的加速度,就需要对P物块的运动做更加巧妙的分解。首先对物块P在运动过程中的任意一个时刻进行受力分析及运动状态分析。
物块P从A到B的运动过程中,P始终沿杆做竖直向上的直线运动,所以P受到向下的重力,沿绳方向的拉力,水平向左的杆的弹力,这三个力的合力始终沿杆方向,先向上后向下,取合外力向上的一个时刻为例来分析(合外力向下时,把所有力反向即可)。如图8所示,首先把物块P沿杆向上的速度v分解为沿绳方向上的分速度v1和垂直于绳方向上的分速度v2,再把物块P受到的合外力F分解为沿绳方向上的F1和垂直于绳方向上的F2,再进一步把F1等效分解为沿绳方向指向O点的向心力F向和沿绳方向上的另一个力F线,F线有可能指向O点,也有可能背向O点,如图9所示。

图9

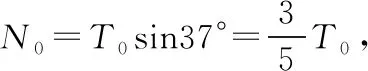
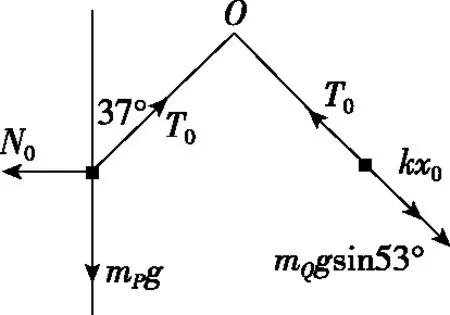
图10
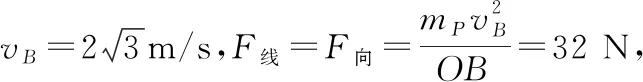
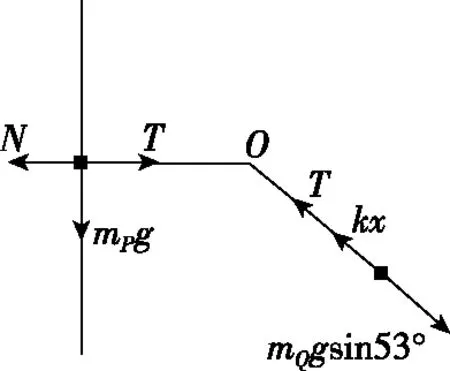
图11
由上面计算可知B选项是错误的。Q在撤去外力时的加速度为沿斜面向下的加速度aQ0=6.4 m/s2,到达B点时的加速度是沿斜面向上的加速度aQ=40 m/s2,整个过程是渐变的过程,所以Q的加速度先减小后反向增大,C错。综上所述,本题答案为D。
通过以上四个例题的解析,我们可以看到,当遇到较为复杂的曲线运动或某些涉及牵连物体的直线运动问题时,可以采用另类运动的合成和分解方法,巧妙地把不熟悉的运动转化为熟悉的运动来处理,就可以达到化繁为简的目的,解决常规方法解决不了的问题。不但能够帮助学生解决问题,也可以促进学生思维训练,提升学习兴趣。
