新型引射式逆流控制矢量喷管的气动性能

2022-05-07王建明夏瑄泽刘晓东王成军

滨州学院学报 2022年2期

王建明，夏瑄泽，刘晓东，王成军

(1.沈阳航空航天大学航空发动机学院;2.沈阳航空航天大学辽宁省航空推进系统先进测试技术重点实验室,辽宁沈阳 110136)

随着航空工业的发展，未来飞行器对于超机动性和短距离起降的需求愈发紧迫，而矢量喷管技术正是提高飞行器的机动性与操纵性的关键技术[1-3]。矢量喷管分为机械矢量喷管和流体矢量喷管[4]，其中流体矢量喷管具有结构简单、易于维修、可靠性高等优点[5]。如今流体矢量喷管已经发展出激波矢量控制[6]、双喉道控制[7]、喉道倾斜控制[8]、逆流控制[9]等。逆流控制由于具有能够实现较大的推力矢量角，且推力损失少、二次流量的需求小、喷管出口主流为亚音速或超音速均可使用等优点，成为较瞩目的流体矢量喷管技术之一[10-11]。逆流控制矢量喷管的工作原理是在矩形收扩喷管外部加装一个外套，并在喷管出口上下形成二次流通道，启动二次流通道内的抽吸系统，外套上下产生压差，使主流发生偏转。

逆流控制矢量喷管是Strykowski等率先提出的一种流体矢量喷管，其对二元喷管出口马赫数为2的单轴逆流推力矢量的技术方案进行实验，得到的最大矢量角为16°[12-13]。此后国内外学者对于逆流控制矢量喷管进行了相应的研究，Deere总结了NASA兰利研究中心的实验与数值仿真计算结果，找到了有利于逆流控制矢量喷管性能的几何参数[14]。Lim等通过数值仿真计算研究了不同主喷管压力比条件下，主流附体现象发生时的附体点的位置，得出当抽吸质量流量与主流质量流量比为5%时会产生矢量推力[15]。汪明生等通过数值模拟的方法研究了逆流控制矢量喷管的非顶层内流特性，及几何参数对喷管性能影响[16-17];史经纬等研究了逆流控制矢量喷管主流附体的产生机理及实现附体主流脱体的方法[18]；刘赵淼等研究了外流马赫数对逆流控制矢量喷管性能的影响[19]。

为了能够进一步提高逆流控制矢量喷管的矢量推力性能，本文在原喷管模型的基础上，提出了一种引射式逆流控制矢量喷管，称为改进型喷管。其改进的结构是在外套管尾部沿切线方向增加一个引射通道，并分析引射及其压强变化对于喷管流场及矢量角的影响。

1 数值计算方法

1.1 计算模型

本文研究的引射式逆流控制矢量喷管是基于文献[13]的逆流控制矢量喷管模型所改进的。原型结构如图1(a)所示，喷管出口截面高度H=0.013 m，主喷管膨胀比(主喷管出口面积/喉道面积)π=1.69，设计落压比NPRD=7.824,二次流通道高度G=0.007 54 m，外套管轴向长度L=0.089 7 m，横向高度C=0.021 m，模型坐标原点在主喷管出口中心处，其中X轴平行于喷管出口方向，Y轴垂直于喷管出口方向向上，Z轴与XY轴满足右手定则。在原型喷管的基础上，于外套管尾部处增加一个引射通道，改进后的喷管如图1(b)所示，引射角度θ=23°，引射通道高度B=0.002 m。

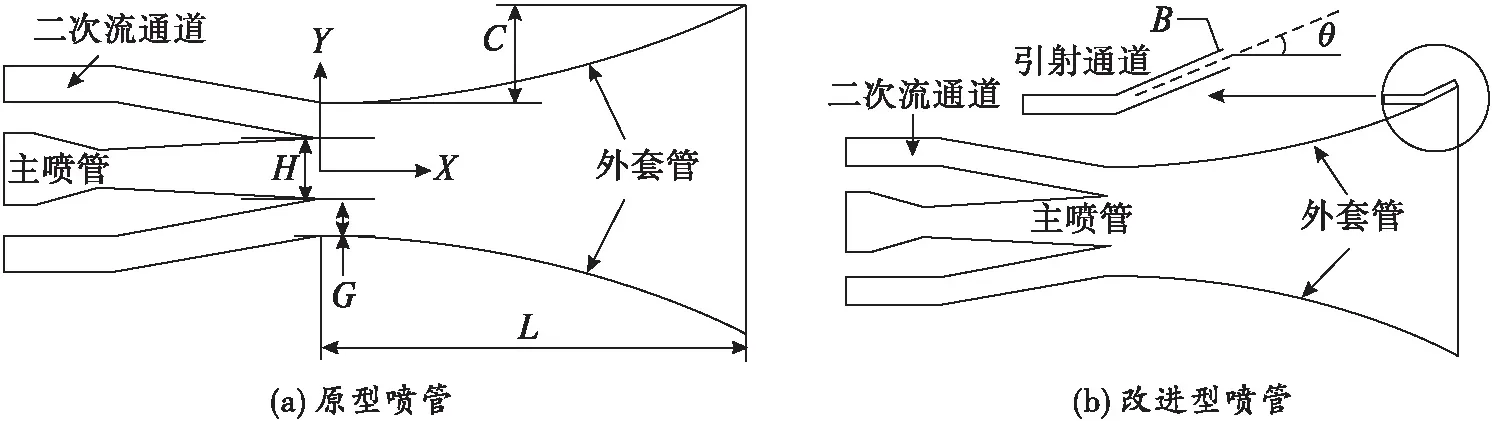
图1 计算模型

1.2 计算网格及参数设置

对引射式流逆流控制矢量喷管模型采用分区生成结构化网格方法，共分成6个区：主喷管内流区域、逆向流区域、同向流区域、引射区域、外套管内的矢量化流场区域以及外流场区域。对于近壁面处的边界层进行加密处理，第一层网格的y+<1，对同向及逆向流区域内的剪切层进行局部加密处理。图2为三维引射式流逆流控制矢量喷管的计算域及喷管模型的内流场网格。

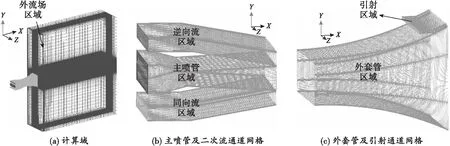
图2 计算域及内流场网格

选用Fluent软件进行数值模拟，选用可实现的k-ε湍流模型，参考文献[13]给定的边界条件：喷管主流进口总压强为0.79 MPa，同向二次流总压强为0.10 MPa，引射总压强为0.11～0.20 MPa，三者均给定为压力入口；逆向二次流抽吸压为0.08 MPa，给定为压力出口；喷管主流，同向、逆向二次流及引射总温度均为300 K；外流场入口总压强为0.10 MPa，给定为压力出口，总温度300 K；所有壁面均给定为绝热无滑移固壁边界。

喷管内流各性能参数计算公式如下:

推力矢量角

(1)

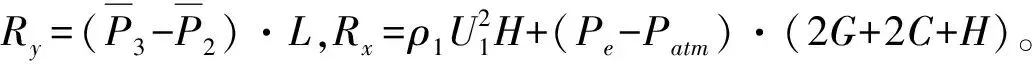
推力系数

(2)

其中,P2、P3分别为逆向二次流及同向二次流入口的压力,ρ1、U1表示主流出口处的密度及速度，Pe为外套管出口处的压力，Ry、Rx分别为飞机为发动机提供的轴向y及径向x的支撑力分力,mi为主流的质量流量,T0、P0为主喷管入口处的滞止温度及压力。

2 计算结果与分析

2.1 计算准确性验证

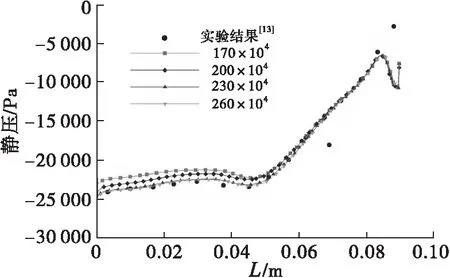
图3 计算结果与实验结果的对比及网格无关性验证

为了验证数值模拟计算的准确性，保持其他参数不变，取抽吸压力P2=0.076 MPa进行计算，同时网格的数量关系着数值模拟的准确性，为了保证计算的准确性，同时对网格进行无关性验证。如图3所示，分别对170×104、200×104、230×104和260×1044种网格进行计算，其中当网格数量为230×104时，计算结果曲线与文献[13]的实验结果基本吻合，但是在外套管上壁面末端计算数据与实验数据存在差别。分析其原因：实验中对于外套管上壁面的压力监测采用取点测量的方法，两点之间距离稍远，未能监测到上壁面末端在两点之间的压力变化，仿真计算的网格节点更加密集，因此能监测到外套管尾部的压力变化。当网格数量≥230×104时，外套管上壁面静压分布基本不再变化，且此时计算速度相对较快。因此选取模型网格数量为230×104进行计算。综上所述，本文的数值模拟研究结果是可信的。

2.2 增强型喷管与原型喷管的结果对比

为研究引射式逆流控制矢量喷管的流场和性能参数，并与原型喷管进行比较，确保两喷管的其他参数不变，取改进型喷管的引射压强为0.20 MPa，对原型和改进型喷管进行计算。

压力系数

(3)

其中,Pin为主喷管进口静压，ρin与vin为主喷管入口气流的密度与速度。

图4为沿原型喷管与改进型喷管Z轴方向与X轴方向压力系数分布的截面图。图4(a)、4(b)分别为两喷管的一系列Z截面，在外套管下游主流上侧处，原型喷管的压力系数大于改进型喷管的压力系数。在外套管出口位置处原型喷管的主流上下两侧压力系数基本一致，而相同区域的改进型喷管主流上侧压力系数明显小于主流下侧压力系数，具体差别如图5所示。

图4(c)、4(d)分别为两喷管的一系列X截面，原型喷管与改型喷管在外套管内以X=0.045 m处(图中箭头所指截面)为界，改进型喷管在X>0.045 m区域的压力系数小于原型喷管。两喷管在X<0.045 m区域的主流上下两侧压力系数基本一致。

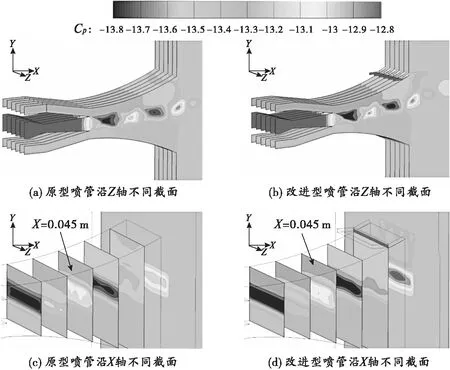
图4 两喷管沿Z轴与X轴不同截面的压力系数分布

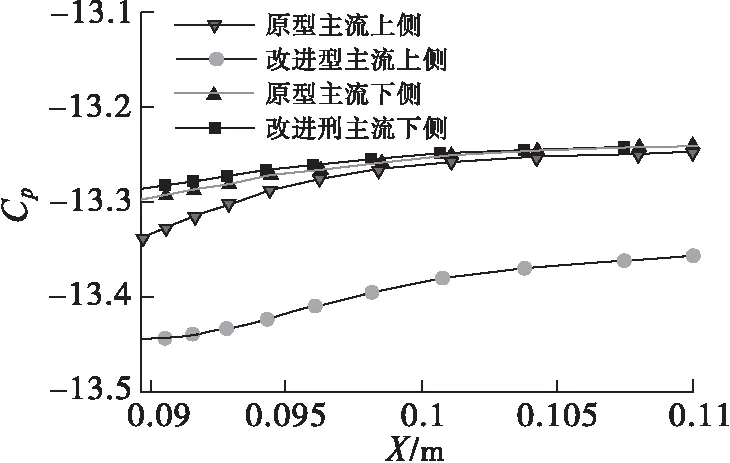
图5 两喷管外套管出口处主流上下两侧压力系数分布

通过沿Z轴与X轴截面对比可以看出改进型喷管的引射明显改变了外套管内部及出口处主流上侧的流场结构，使上侧压力降低，导致主流上下两侧压差增大，使得主流偏转角度增加。从图4可以看到，两喷管的压力系数分布沿对称面两侧基本一致，因此通过研究对称面(Z=0)处的流动结构来揭示喷管三维流场结构的变化是可行的。

图6为原型喷管与改进型喷管在Z=0处截面的马赫分布云图。如图6所示，此时原型喷管的推力矢量角为10.42°，推力系数为96.33%；改进型喷管的推力矢量角为13.31°，推力系数为97.05%，与原型喷管相比，改进型喷管在外套管尾部增加一股引射射流。由于引射射流与主流都属于高速射流，在外流场流动时会卷吸周围大气，且引射射流与主流之间距离较近，两股气流之间相互吸引使得主流向上偏移。改进型喷管在同等工况下，通过高速引射射流使推力矢量角提升2.89°，推力系数提升0.72%。

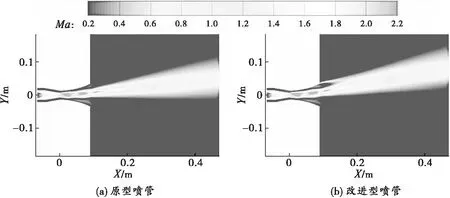
图6 两喷管在Z=0处截面的马赫数分布

2.3 引射式逆流控制矢量喷管的机理分析

图7为原型喷管与改进型喷管Z=0处截面的压力系数云图对比。如图7(a)所示，在原型喷管的外套管内部上侧，压力系数沿X轴方向，从左侧低压力系数区向右逐渐增大，经由过渡区域，最终与外流场大气相同，在外套管出口位置，通过观察等值线可以发现，主流上下两侧的压力系数沿X轴基本相同，当主流射出外套管后，主流两侧不再出现压差。在图7(b)中，由于外套管尾端引射的影响，在改进型喷管的外套管内部上侧，左侧低压力系数区与过渡区域同时向外扩张，并且过渡区域在外套管出口处，形成一道弧形边界(图7(b)中圆圈标识区域)。与原型喷管相比，改进型喷管的外套管内部上侧的总体压力系数更低，当主流射出外套管后，在一定区域内，主流两侧仍存在压差。

低压力系数区域与过渡区域向外扩张的原因在于：弧形边界所在的区域上下存在引射射流与主流两股高速气流，这两股高速气流在弧形边界右侧汇合射出，使得外套管内部的低压气流无法与外流场大气直接接触提高压强，导致低压力系数区与过渡区域向外扩张，并在射流与主流汇合处形成弧形边界。结合Z轴与X轴各截面与Z=0处截面的压力系数分析可知，改进型喷管矢量角增大的原因在于：总体上主流两侧的压差增大。这是改进型喷管推力矢量角提高的第一个原因。

图7 两喷管在Z=0处截面的压力系数分布

图8为原型喷管与改进型喷管外套管内及出口处Z=0的矢量流线分布。如图8(a)所示，主流流线在外套管尾部区域沿来时白色箭头方向射出，而在图8(b)中，主流上侧出现大尺度涡结构，同时在圆圈处可以看到，主流上侧的流体先随着涡结构向上偏转接触到引射气流，而后随引射气流再次汇入主流。结合前文Z=0处截面的马赫数分析所述，验证了距离较近的两股高速射流产生的卷吸效应，会相互吸引流体汇合，使得主流上侧流体向上偏转，同时带动主流整体向上。这是改进型喷管推力矢量角提高的第二个原因。

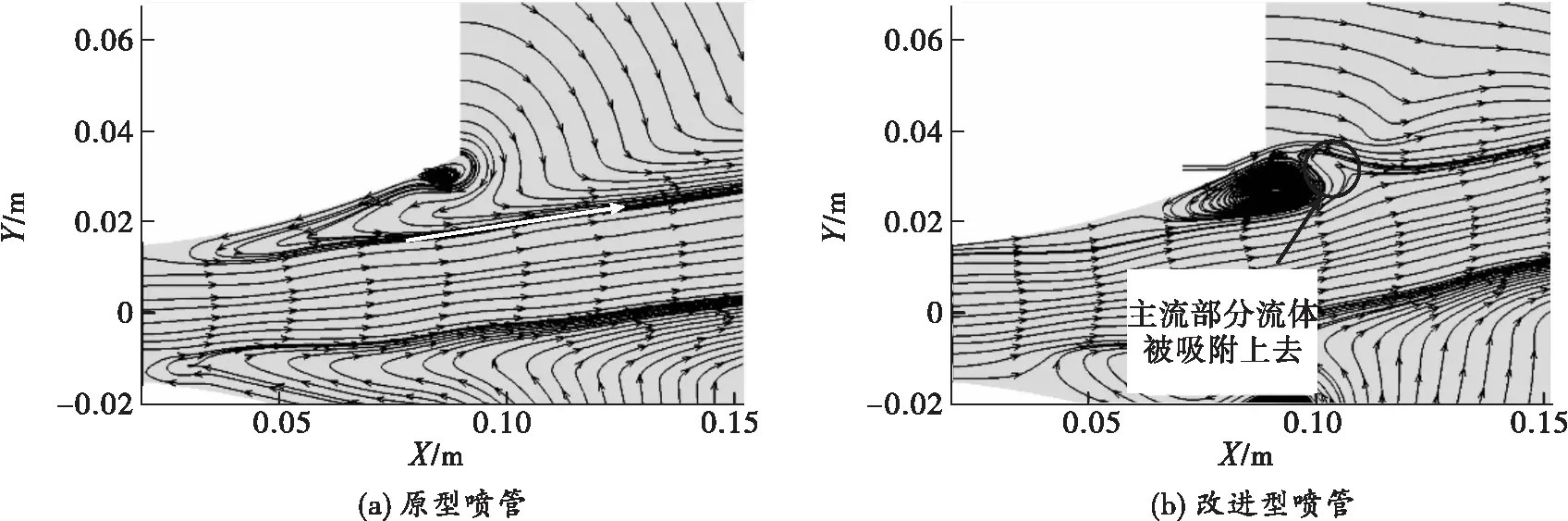
图8 两喷管在Z=0处截面的矢量流线分布

2.4 引射压强对引射式逆流控制矢量喷管性能参数的影响

为了进一步探索引射压强对改进型喷管性能参数及流场结构的影响，本文保持其他参数不变，以引射压强P4为变量，取P4为0.11～ 0.20 MPa时分析引射压强变化对喷管推力矢量角与推力系数的影响。

图9为引射式逆流控制矢量喷管推力矢量角和推力系数CT随引射压强P4的变化曲线。从图9(a)可以看到，在引射压强P4从0.11 MPa增加到0.20 MPa的过程中，推力矢量角整体呈线性增长趋势。从图9(b)中可以看到随着引射压强的增加，CT在初期呈下降趋势(P4<0.13 MPa)，随着引射压强的继续增加,在0.14～0.18 MPa，CT开始出现下降、增大再下降的波动现象，其中0.15 MPa与0.18 MPa对应的推力系数都处于对应波动的最低点。当引射压强增大到0.19 MPa以上时，推力系数增大到最高点并保持不变。具体数据如表1所示，当P4=0.20 MPa时，推力矢量角达到了13.31°，推力系数达到97.05%，此时的喷管具有最好的矢量性能。

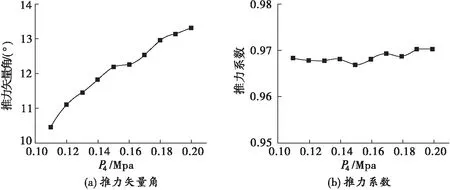
图9 不同引射压强对推力矢量角和推力系数的影响

推力系数产生波动的原因：如前文所述，引射会对外套管内部的压力及流场产生影响，主要变化部位在外套管出口处，因此会对Pe产生影响，进而影响推力系数。随着引射压强逐渐增加，引射中的气流从随大气被吸入近外套管，到直接汇入进主流的过程中，Pe相较于原型喷管的数值一直在逐渐降低，因此从整体上看推力系数有所提高。但Pe的数值对于推力系数整体计算而言影响较小，因此推力系数整体会存在数值较小的波动现象。

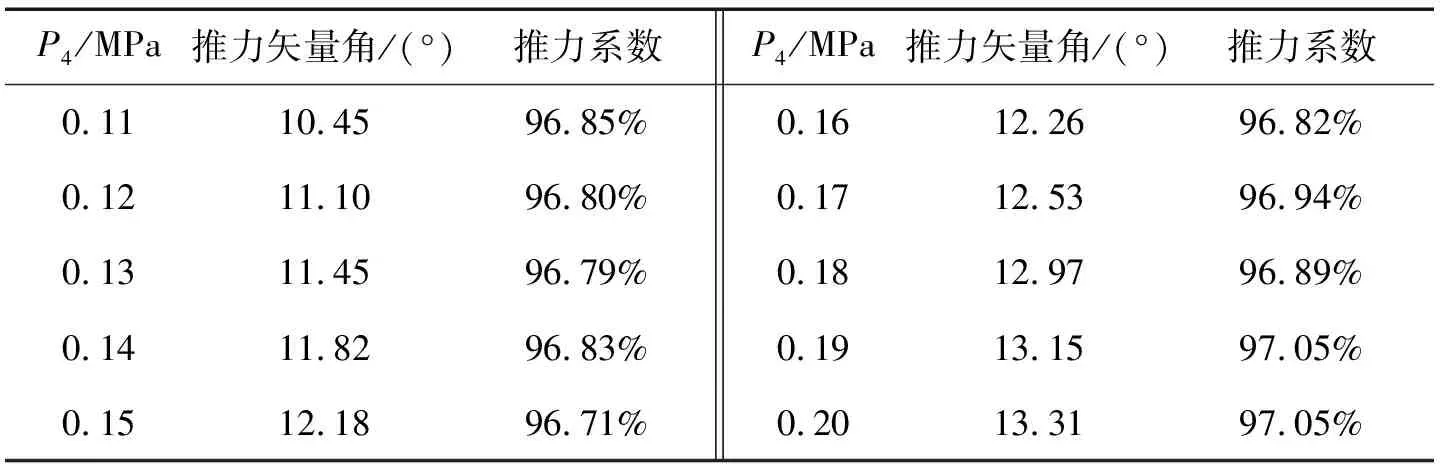
表1 不同引射压强下推力矢量角与推力系数

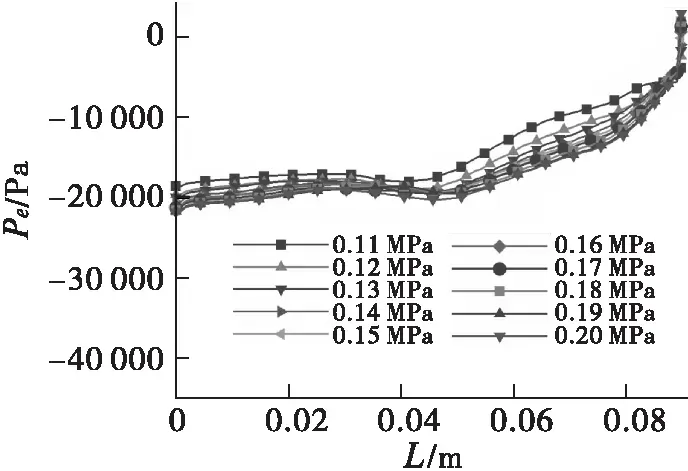
图10 不同引射压强下外套管上壁面静压分布

推力矢量角和推力系数是喷管气动效率的重要参数之一，随着引射压强的增加改进型喷管的推力矢量角持续增大，推力系数虽然有所波动，但从整体看呈上升趋势，因此引射压强的增大对改进型喷管的气动效率有明显提高。

图10为引射式逆流控制矢量喷管在不同引射压强下外套管上壁面的静压分布。从图中可以看到随着射流压力的增加，在外套管前方(X<0.04 m)的静压有所降低，相对于前方外套管后方的部静压开始变大，并在尾部出现压力快速增大。当引射压强为0.11 MPa时，在外套管(X>0.08)位置压力先由增长转为平稳后再在尾部有小幅度的快速增大。当引射压强由0.12 MPa变化到0.20 MPa时，外套管压力分布曲线变化趋势基本相同，只有尾部位置的静压随引射压强的增大而提高。外套管上下壁面的压力分布是逆流控制矢量喷管推力矢量角的重要影响因素，外套管上壁面的压力分布整体上随着引射压强的增大而减小，外套管下壁面压力分布基本保持不变，因此使主流两侧的压力差增大从而导致推力矢量角增大。